РЕФЕРАТ
на тему:”Найпростіші задачі квантової механіки”
План
1. Рух вільної частинки
2. Частинка в одновимірному потенціальному ящику
3. Гармонічний квантовий осцилятор
4. Проходження частинки крізь потенціальний бар’єр. Тунельний ефект
1
. Рух вільної частинки
Найпростішим рухом квантової частинки є вільний рух. Прикладом такого руху є рух електронів в металах і напівпровідниках. В цьому випадку потенціальна енергія частинок дорівнює нулю. При вільному русі повна енергія частинки збігається з кінетичною, а її швидкість є сталою величиною. Такому рухові в класичній механіці відповідає рівномірний і прямолінійний рух.
Нехай рівномірний рух квантової частинки відбувається в напрямі осі х
, яка збігається з напрямком вектора швидкості. Стаціонарне рівняння Шредінгера для вільної частинки запишеться:
 (1.3.15) (1.3.15)
де m
― маса частинки; Е
― повна енергія частинки.
Рівняння (1.3.15) є диференціальним рівнянням другого порядку зі сталими коефіцієнтами, розв’язком якого може бути функція
 (1.3.16) (1.3.16)
де А
і к
― сталі величини; і
― уявна одиниця.
Підстановка (1.3.16) в (1.3.15) дасть тотожність

звідки
 (1.3.17) (1.3.17)
У співвідношенні (1.3.17) к
- хвильове число хвиль де Бройля; Е
― повна енергія частинки; m
― маса частинки.
Енергія вільної частинки з рівності (1.3.17) дорівнює
 (1.3.18) (1.3.18)
Хвильове число к
може набувати довільних значень, тому що вільні частинки в системі можуть мати практично будь-які постійні швидкості. Це говорить про те, що енергетичний спектр вільних частинок є суцільним.
Густина імовірності перебування вільної частинки в довільних точках осі х
дорівнює

де  - комплексно спряжена хвильова функція. Звідки - комплексно спряжена хвильова функція. Звідки

Густина імовірності вільної частинки в будь-якій точці осі х
є сталою величиною. Невизначеності вільної частинки в координаті в такому випадку дорівнюють безмежності. Цей висновок є добрим підтвердженням співвідношення невизначеностей Гейзенберга.
2.
Частинка в одновимірному потенціальному ящику
Розглянемо приклад просторово-обмеженого одновимірного руху квантової частинки в глибокому потенціальному ящику з вертикальними стінками, шириною l
. Потенціальна енергія електрона зовні і всередині такого ящика має наступні значення:
U
(
x
)=0
при 0<
x
<
l
, (1.3.19)
U
(
x
)=
при x
0
й x
l
.
Графік залежності потенціальної енергії частинки U
(
x
)
від х
показаний на рис 1.5.
Частинка в такому ящику може вільно рухатись на ділянці 0хl
. На кінцях цього інтервалу вона стикається з абсолютно твердими стінками. Непрозорість цих стінок визначається необмеженим ростом потенціальної енергії U
(
x
)
в точках х=0
і х
=l
.

Рис. 1.5
Прикладом руху електрона в потенціальному ящику може бути рух колективізованих електронів усередині металу. Як відомо, у класичній електронній теорії вважали, що поза металом потенціальна енергія електрона дорівнює нулю, а всередині металу ― вона від’ємна і чисельно дорівнює роботі виходу електрона з металу. Інакше кажучи, вважали, що рух електронів обмежений потенціальним бар’єром прямокутної форми з плоским дном. У нашому випадку потенціальний ящик значно простішої форми ніж реальний випадок електрона в металі.
Оскільки частинка не виходить за межі ділянки 0 х
l
, то імовірність знайти її за межами цієї ділянки дорівнює нулю. Це означає, що рівняння Шредінгера для стаціонарних станів можна доповнити граничними умовами  і і 
Запишемо рівняння Шредінгера для частинки в потенціальному ящику
 (1.3.20) (1.3.20)
де m
― маса частинки;  ― стала Дірака; Е
― повна енергія частинки; (х)
― хвильова функція. ― стала Дірака; Е
― повна енергія частинки; (х)
― хвильова функція.
Введемо позначення
 (1.3.21) (1.3.21)
де к
― хвильове число хвиль де Бройля для електрона, який перебуває всередині потенціального ящика.
Рівняння (1.3.20) набуде вигляду
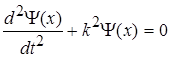 . (1.3.22) . (1.3.22)
Знайдемо розв’язок рівняння (1.3.22), подібно до аналогічних диференціальних рівнянь гармонічних коливань, у тригонометричній формі
 (1.3.23) (1.3.23)
де А, В
і С
─ сталі величини.
З граничних умов одержуємо:
а) (0)=0
; 0=АcosB.
0+CsinB.
0,
звідки А=0
; В0
і С0
.
б) (l)=0
; 0=CsinB.
l,
звідки при С0, Вl=n
, або  де n = 1,2,3,
... де n = 1,2,3,
...
Хвильова функція з урахуванням граничних умов набуде вигляду:
 (1.3.24) (1.3.24)
Константу С
у формулі (1.3.24) знайдемо з умови нормування
 , (1.3.25) , (1.3.25)
або
 . (1.3.26) . (1.3.26)
Другий інтеграл у виразі (1.3.26) для будь-яких значень n
дорівнює нулю, тому
 , звідки , звідки 
Хвильова функція, яка описує квантовий рух частинки в потенціальному ящику, має вигляд:
 (1.3.27) (1.3.27)
При підстановці (1.3.27) у (1.3.22) одержуємо тотожність
 , ,
звідки
 (1.3.28) (1.3.28)
Енергія Е електрона в потенціальному ящику не може бути довільною. Вона набуває лише дискретних власних значень Е(n)
. Імовірність виявити в межах потенціального ящика електрон з іншою енергією, ніж (1.3.28) дорівнює нулю.
Що ми одержали в результаті розв’язування рівняння Шредінгера? По-перше,
набір псі-функцій
, які залежать від квантового числа n
. По-друге, значення енергії Е
, при яких розв’язок рівняння Шредінгера має фізичний зміст. По-третє, розподіл імовірності
виявлення частинки в різних точках осі x
усередині ящика. Подібні ж результати виходять при розв’язуванні рівняння Шредінгера й в інших випадках, наприклад, для атома водню.
Енергетичний спектр і густина імовірності частинки в потенціальному ящику показана на рис. 1.6.
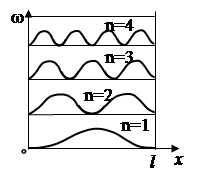
Рис. 1.6
Число n у формулі (1.3.28) визначає вид хвильової функції й енергію частинки в стані з цією хвильовою функцією і називається квантовим числом
. Покажемо, що для частинки в потенціальному ящику можливі лише такі енергетичні рівні, на яких на ширині ящика вкладається лише ціле число півхвиль де Бройля. При аналізі граничних умов було показано, що kl
=
n
, де  ― хвильове число хвиль де Бройля. З урахуванням останнього маємо: ― хвильове число хвиль де Бройля. З урахуванням останнього маємо:
 (1.3.29) (1.3.29)
Співвідношення (1.3.29) показує, що в потенціальному ящику можливі лише такі стани частинки, при яких на ширині потенціального ящика l
вкладається ціле число півхвиль де Бройля (рис. 1.7).
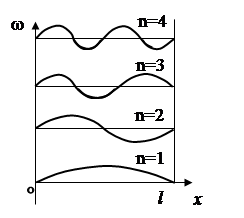
Рис. 1.7
Незбуреному стану частинки (n=1) відповідає енергія
 (1.3.30) (1.3.30)
Значення цієї енергії Е
l
0
свідчить про те, що частинка в потенціальному ящику ніколи не зупиняється і що невизначеність Рх
імпульсу частинки не може бути меншою за величину
 (1.3.31) (1.3.31)
В потенціальному ящику шириною l
положення частинки визнача-ється похибкою, яка сумірна з його шириною хl,
тому що перебуває у повній відповідності із співвідношенням невизначеностей імпульс - координата.
Покажемо, як залежить ширина енергетичного інтервалу Е
від розмірів потенціального ящика. У потенціальному ящику з розмірами l=10-9
м
власні значення енергії електрона утворюють послідовність енергетичних рівнів, енергетична відстань між якими дорівнює
E=En+1
-En
,
або
 Дж. Дж.
В електрон-вольтах ця енергія буде дорівнювати

Цей розрахунок показує, що коли ширина потенціального ящика сумірна з розмірами атома (10-10
м), енергетичний інтервал між сусідніми енергетичними рівнями досить значний, а спектр є дискретним.
У випадку, коли потенціальний ящик має макроскопічні розміри l10-2
м
, енергетичний інтервал між сусідніми рівнями буде дорівнювати
 Дж=0,34.
10-14
(2n+1) eB. Дж=0,34.
10-14
(2n+1) eB.
Для такого потенціального ящика квантуванням енергії можна знехтувати. Вона нічим не відрізняються від значень енергії, одержаних класичними методами.
Аналогічні результати можна одержати для великих квантових чисел n
. У цьому випадку проявляється принцип відносності, встановлений Бором у 1923 р.
При великих квантових числах висновки й результати квантової механіки збігаються з відповідними класичними результатами.
3. Гармонічний квантовий осцилятор
Просторово-обмеженим є також рух квантового осцилятора. З класичної точки зору осцилятором може бути будь-яка матеріальна точка, яка здійснює гармонічні коливання під дією квазіпружної сили
F
=-
kx
, де k
=
m
 . (1.3.33) . (1.3.33)
Потенціальна енергія класичного осцилятора знаходиться за формулою
 (1.3.34) (1.3.34)
де m
― маса частинки;  ― циклічна частота осцилятора. ― циклічна частота осцилятора.
Графічна залежність потенціальної енергії класичного осцилятора показана на рис. 1.8.

Рис. 1.8
З рисунка видно, що осцилятор може мати практично довільну енергію, навіть рівну нулю. В точках -а
і +а
кінетична енергія осцилятора дорівнює нулю, а потенціальна енергія досягає свого максимуму. За межі області (-а, +а)
класичний осцилятор вийти не може.
Квантовим осцилятором може бути лише елементарна частинка, яка поряд із корпускулярними властивостями проявляє і хвильові властивості. Прикладом квантового осцилятора може бути коливний рух атомів і молекул у вузлах кристалічної гратки. Потенціальна енергія квантового осцилятора має ту ж математичну залежність, що і класичний осцилятор (1.3.34).
Стаціонарне рівняння Шредінгера для лінійного гармонічного осцилятора має вигляд:
 (1.3.35) (1.3.35)
де m
―
маса квантової частинки;  ― власна циклічна частота; Е
― повна енергія частинки. ― власна циклічна частота; Е
― повна енергія частинки.
Знаходження хвильових функцій квантового осцилятора є досить складною математичною задачею. Тому, опускаючи такі розв’язки, наводимо енергетичний спектр квантового осцилятора. Він має вигляд
 (1.3.36) (1.3.36)
де n
= 0,1,2,3,
... ― будь-яке ціле число, починаючи з нуля;  ― власна циклічна частота осцилятора; ― власна циклічна частота осцилятора;  ― стала Дірака. ― стала Дірака.
Аналіз рівняння (1.3.36) показує, що енергетичний спектр квантового осцилятора є дискретним і що власні значення енергії дорівнюють:
 , ,  , , 
В енергетичному спектрі (1.3.36) проміжки між енергетичними рівнями не залежать від квантового числа n
, а є однаковими
 (1.3.37) (1.3.37)
Як показано на рис. 1.9, де енергетичний спектр квантового осцилятора суміщається з аналогічним спектром класичного осцилятора, квантовий осцилятор не має значень енергії рівних нулю.
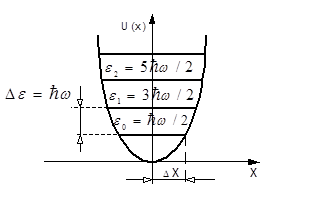
Рис.1.9
Найменше значення енергії квантового осцилятора дорівнює
 . (1.3.38) . (1.3.38)
Меншої енергії квантовий осцилятор не може мати навіть при абсолютному нулі температур.
Покажемо наближеним способом, що енергія квантового осцилятора квантується. З рис 1.10 видно, що на відрізкуl
=2х0
вкладається ціле число півхвиль де Бройля, тобто
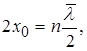 (1.3.39) (1.3.39)
де  ― середнє значення довжини хвилі де Бройля. ― середнє значення довжини хвилі де Бройля.
Звідки
 (1.3.40) (1.3.40)
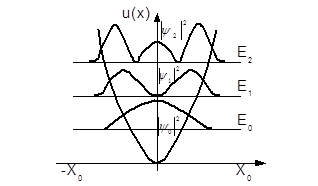
Рис. 1.10
Середнє значення імпульсу кванта хвилі де Бройля
 (1.3.41) (1.3.41)
Середня кінетична енергія такого осцилятора
 (1.3.42) (1.3.42)
Відомо, що повна енергія Е
перевищує середнє значення кінетичної енергії у два рази, тобто
 (1.3.43) (1.3.43)
З іншої точки зору повна енергія квантового осцилятора дорівнюватиме максимальній потенціальній енергії
 (1.3.44) (1.3.44)
Перемножимо рівності (1.3.43) і (1.3.44), одержимо
 (1.3.45) (1.3.45)
або
 (1.3.46) (1.3.46)
В межах точності наших міркувань  1, тому 1, тому
 (1.3.47) (1.3.47)
де n
=1,2,3
,... ― цілі числа.
Наближений розрахунок показує, що енергія квантового осцилятора набуває ряду дискретних значень, тобто квантується.
Точне значення енергії для не збудженого квантового осцилятора нульового рівня можна одержати з рівняння Шредінгера (1.3.35), якщо згідно з рис. 1.10 скористатись функцією Гаусса, яка дорівнює
 (1.3.48) (1.3.48)
де а
― стала величина, яку слід визначити.
Другу похідну від (1.3.48) підставимо в (1.3.35)

звідки
 . (1.3.49) . (1.3.49)
Тотожність (1.3.49) має місце у випадку рівності коефіцієнтів при х2
і вільних членів, тобто
  (1.3.50) (1.3.50)
Система рівнянь (1.3.50) дає можливість одержати значення енергії Е
і сталої величини а
  . (1.3.51) . (1.3.51)
Таким чином функція Гаусса є розв’язком рівняння Шредінгера (1.3.35) лише за умови коли  . .
В цьому випадку
 . (1.3.52) . (1.3.52)
Слід відмітити, що оскільки відстань між суміжними рівнями енергії квантового осцилятора дорівнює  то з урахуванням то з урахуванням  одержуємо енергетичний спектр квантового осцилятора у вигляді одержуємо енергетичний спектр квантового осцилятора у вигляді
 (1.3.53) (1.3.53)
де n
= 0,1,2,3,
...
4.
Проходження частинки крізь потенціальний бар’єр.Тунельний ефект
Класична частинка не може перебувати в тих місцях, де її потенціальна енергія U(x)
перевищувала б повну енергію частинки E
. Щодо квантової частинки, то вона має таку властивість через те, що існує відмінна від нуля імовірність проникнення її крізь потенціальний бар’єр, тобто в область, де U(x) E.
Проведемо оцінку цієї імовірності шляхом розв’язування такої задачі. Нехай квантова частинка з масою m
, рухаючись в напрямі осі х
, вдаряється в потенціальний бар’єр кінцевої висоти U
0
, тобто

причому енергія частинки Е
менша висоти бар’єра U
0
, (рис. 1.11).

Рис. 1.11
В області потенціального бар’єра рівняння Шредінгера для стаціонарних станів набуде вигляду
 (1.3.54) (1.3.54)
Якщо позначити вираз  через через  , то рівняння (1.3.54) перепишеться , то рівняння (1.3.54) перепишеться
 . (1.3.55) . (1.3.55)
Розв’язком рівняння (1.3.55) може бути функція
 , (1.3.56) , (1.3.56)
де А
і В ─
деякі константи.
Експонента з додатним знаком фізичного змісту не має й може бути відкинута, тому що не повинно бути зростання імовірності в області потенціального бар’єра. Тому в області потенціального бар’єра (х
), хвильова функція частинки
x
визначається рівністю
x
= А
e
-
 x
.
(1.3.57) x
.
(1.3.57)
Коефіцієнт А
у виразі (1.3.57) пов’язаний з інтенсивністю променя частинок, які рухаються у напрямі бар’єра, а тому задається довільно. Як правило для х
координати частинок розподіляються з густиною імовірності
 , (1.3.58) , (1.3.58)
де 0
дорівнює значенню
x
2
при х=0.
Рівняння (1.3.58) показує, що із збільшенням глибини проникнення в область потенціального бар’єра, густина імовірності х
зменшується експоненційно. Це зменшення буде тим швидше, чим більша різниця енергій U0
- E.
Знайдемо глибину проникнення елементарної частинки в область потенціального бар’єра при умові, що m
= 9,1 10-31
кг
(електрон), U0
- E =
10-4
eB
, а густина імовірності (х
на цій відстані зменшується в е
разів
 . .
Ця відстань перевищує на два порядки діаметр атома водню. Глибина проникнення зменшується на порядок, якщо різниця енергій U
0
-
E
зросте до 10-2
еВ
.
Здатність квантових частинок проникати в область потенціального бар’єра приводить до тунельного ефекту.
Його суть полягає в проникненні частинки з однієї області в іншу область, які поділені потенціальним бар’єром навіть в тих випадках, коли енергія частинки Е
менша висоти потенціального бар’єра U0
.
Таке проходження частинки виявляється можливим дякуючи існуванню під бар’єром хвильової функції, яка «прокладає» шлях частинці на будь-яку відстань. Тунельний ефект є головною причиною -розпаду радіоактивних ядер.
|