31. Определение предела числовой функции. Односторонние пределы. Свойства пределов.
Число А называется пределом функции y=f(x) в точке х0
, если для любой последовательности допустимых значений аргумента xn
, n€N (xn
≠x0
), сходящейся к х0
(т.е. 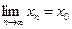 ), последовательность соответствующих значений функции f(xn
), n€N, сходится к числу А, т.е. ), последовательность соответствующих значений функции f(xn
), n€N, сходится к числу А, т.е. 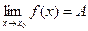 . Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х0
, соответствующие значения функции как угодно мало отличается от числа А. . Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х0
, соответствующие значения функции как угодно мало отличается от числа А.
Односторонние пределы.
Считается, что х стремится к х0
любым способом: оставаясь меньшим, чем х0
(слева от х0
), большим, чем х0
(справа от х0
), или колеблясь около точки х0
.
Число А1
называется пределом функции
y=f(x) слева
в точке х0
, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х€(x0
-σ;x0
), выполняется неравенство |f(x)-A1
|<ε 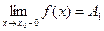
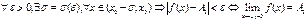
Пределом функции справа
называется

Свойства пределов.
1) если предел 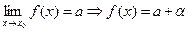 функция равна этому числу плюс б.м. функция равна этому числу плюс б.м.
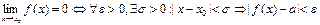
ε – сколь угодно малое число
|f(x)-a|=α; f(x)=a+ α
2) сумма конечного числа б.м. чисел есть б.м. число
3) предел произведения равен произведению пределов
4) константы можно выносить за знак предела
5) 
 32. Замечательные пределы. 32. Замечательные пределы.
1 замечательный предел.
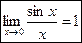
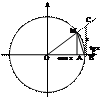
Возьмем круг радиуса 1, обозначим
радианную меру угла MOB через Х.
Пусть 0 < X < π/2. На рисунке |АМ| = sinx, дуга МВ численно равна центральному углу Х, |BC| = tgx. Тогда
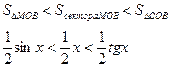
Разделим все на  и получим: и получим:
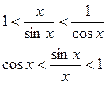
Т.к.  , то по признаку существования пределов следует , то по признаку существования пределов следует  . .
2 замечательный предел.

Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:

Если x→∞, то n→∞, тогда

По признаку о существовании пределов:
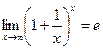
33. Непрерывные функции и их свойства. Точка разрыва функций и их классификация.
Пусть функция y=f(x) определена в точке х0
и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0
, если существует предел функции в этой точке и он равен значению функции в этой точке:
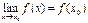
Это означает:
- функция определена в точке х0
и в ее окрестности;
- функция имеет предел при х→х0
- предел функции в точке х0
равен значению функции в этой точке, т.е. выполняется равенство.
Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х0
Точки разрыва функции
– это точки в которых нарушается непрерывность функции.
Точка разрыва х0
называется точкой разрыва 1 рода
функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)
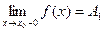 и и 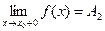
При этом, если:
- А1
=А2
то точка х0
называется точкой устранимого разрыва;
- А1
≠А2
то точка х0
называется точкой конечного разрыва.
|A1
– A2
| называется скачком функции.
Точка разрыва х0
называется точкой разрыва 2 рода
функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.
34. Производная от функции. Дифференцируемость функции. Дифференциал.
Производной функции y=f(x) в точке х0
называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.
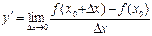
Производная функции f(x) есть некоторая функция
f ’(x), произведенная из данной функции.
Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой
в этом интервале.
Операция нахождения производной называется дифференцированием.
Дифференциал функции
y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).
Иначе.
Дифференциал функции
равен произведению производной этой функции на дифференциал независимой переменной.
35. Правила дифференцирования суммы, произведения, частного функции. Производные сложных функций.
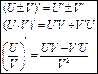
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Производная обратной функции равна обратной величине производной данной функции.
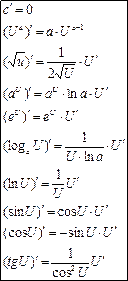 
36. Логарифмическое дифференцирование.
Логарифмическое дифференцирование -
в некоторых случаях целесообразнее функцию сначала прологарифмировать, а результат продифференцировать.

Однако производные степенных функций находят только логарифмическим дифференцированием.
Производная степенно-показательной функции равна сумме производно показательной функции, при условии
U
=
const
, и производной степенной функции, при условии
V
=
const
.
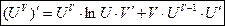
37. Теоремы о среднем. Правило Лопиталя.
Рассмотрим способ раскрытия неопределенностей 0 / 0 и ∞ / ∞
, который основан на применении производных.
Правило Лопиталя, при 0 / 0.
Пусть функции
f
(
x
) и φ(
x
) непрерывны и дифференцируемы в окрестности точки
x
0
и обращается в нуль в этой точке:  . .
Пусть φ ′(
x
) ≠ 0 в окрестности точки
x
0
Если существует предел
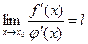 , то , то 
Применим к функциям f(x) и φ(x) теорему Коши для отрезка [x0
;x], лежащего в окрестности точки x0
, тогда
 , где с лежит между x0
и х. , где с лежит между x0
и х.
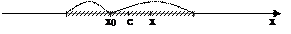
При x→x0
величина с также стремится к х0
; перейдем в предыдущем равенстве к пределу:

Так как 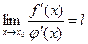 , то , то 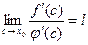 . .
Поэтому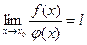
(предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует)
Правило Лопиталя, при ∞ / ∞.
Пусть функции
f
(
x
) и φ(
x
) непрерывны и дифференцируемы в окрестности точки
x
0
(кроме точки
x
0
), в этой окрестности
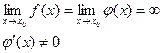
Если существует предел
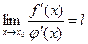 , то , то 
Неопределенности вида 0∙∞ ; ∞-∞ ; 1∞
; ∞0
; 00
сводятся к двум основным.
Например, 0∙∞
Пусть f(x)→0, φ(x)→∞ при х→х0
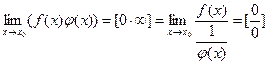
38. Дифференциалы высших порядков.
Пусть y=f(x) дифференцируема функция, а ее аргумент х – независимая переменная. Тогда дифференциал dy=f ′(x)dx есть также функция х, можно найти дифференциал этой функции. Дифференциал от дифференциала есть второй дифференциал.
Производную можно рассматривать, как отношение дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
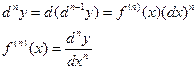 Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной. Дифференциал n-ого порядка, есть дифференциал от дифференциала (n-1)-ого порядка, т.е. производную функции можно рассматривать, как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
39. Исследование условий и построение графиков.
- найти область определения функции
- найти точки пересечения графика с осями координат
- найти интервалы знака постоянства
- исследовать на четность, нечетность
- найти асимптоты графика функции
- найти интервалы монотонности функции
- найти экстремумы функции
- найти интервалы выпуклости и точки перегиба
|