Министерствообразования и науки Украины
Днепропетровский Национальный Университет
Факультет электроники, телекоммуникаций и компьютерных систем
Кафедра АСОИ
Расчётная задача №3
«Исследование математических операций»
Выполнил:
Ст. группы РС-05
Проверил:
Доцент кафедры АСОИ
Саликов В.А.
г. Днепропетровск
2007г.
Условие задачи

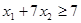
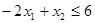
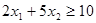

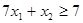
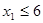
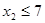
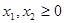
Решение задачи
r = R1
+R2
+…Ri
;
min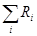 = min(r); = min(r);
Ri
=1,2,….
Полученное на 1 этапе оптимальное базисное решение используется в качестве начального решения исходной задачи.
Основные этапы реализации двухэтапного метода (как и других методов искусственного базиса) следующие:
1. Строится искусственный базис. Находится начальное недопустимое решение. Выполняется переход от начального недопустимого решения к некоторому допустимому решению. Этот переход реализуется путем минимизации (сведения к нулю) искусственной целевой функции, представляющей собой сумму искусственных переменных.
2. Выполняется переход от начального допустимого решения к оптимальному решению.
Все ограничения требуется преобразовать в равенства. Для этого в ограничения «больше или равно» (первое и второе) необходимо ввести избыточные переменные. В ограничение «меньше или равно» (четвертое) добавляется остаточная переменная. В ограничение «равно» не требуется вводить никаких дополнительных переменных. Кроме того, требуется перейти к целевой функции, подлежащей максимизации. Для этого целевая функция Е умножается на -1. Математическая модель задачи в стандартной форме имеет следующий вид:
Первый этап (поиск допустимого решения)
1. Во все ограничения, где нет базисных переменных, вводятся искусственные базисные переменные.
Примечание. Искусственная целевая функция всегда (в любой задаче) подлежит минимизации.
2 Искусственная целевая функция выражается через небазисные переменные. Для этого сначала требуется выразить искусственные переменные через небазисные:
3 Для приведения всей задачи к стандартной форме выполняется переход к искусственной целевой функции, подлежащей максимизации. Для этого она умножается на -1:
4.Определяется начальное решение. Все исходные, а также избыточные переменные задачи являются небазисными, т.е. принимаются равными нулю. Искусственные, а также остаточные переменные образуют начальный базис: они равны правым частям ограничений.
5 Составляется исходная симплекс-таблица. Она отличается от симплекс-таблицы, используемой для обычного симплекс-метода только тем, что в нее добавляется строка искусственной целевой функции. В этой строке указываются коэффициенты искусственной целевой функции (приведенной к стандартной форме, т.е. подлежащей максимизации) с обратными знаками, как и для обычной целевой функции.
6.Выполняется переход от начального недопустимого решения, содержащегося в исходной симплекс-таблице, к некоторому допустимому решению. Для этого с помощью обычных процедур симплекс-метода выполняется минимизация искусственной целевой функции. При этом переменные, включаемые в базис, выбираются по строке искусственной целевой функции. Все остальные действия выполняются точно так же, как в обычном симплекс-методе. В результате минимизации искусственная целевая функция - должна принять нулевое значение. Все искусственные переменные при этом также становятся равными нулю (исключаются из базиса), так как искусственная целевая функция представляет собой их сумму.
Двухэтапный метод
1 шаг
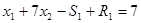

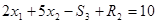
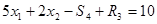

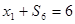
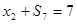
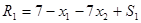


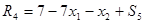
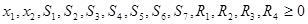
2 шаг
 , где , где 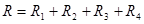
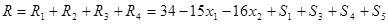
В ходе преобразований имеем:
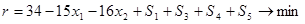
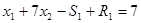

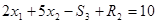
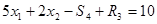

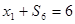
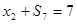
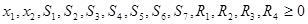
Строим симплекс таблицу:
Итерация 0
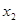 - ведущий столбец - ведущий столбец
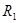 - ведущая строка - ведущая строка
Итерация 1
| Базис
|

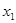
|
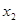 |
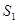 |
 |
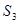 |
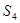 |
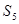 |
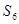 |
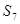 |
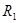 |
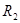 |
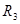 |
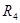 |
Решение
|
Оценка
|
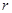 |
12,8571 |
0 |
1,1429 |
0 |
-1 |
-1 |
-1 |
0 |
0 |
-2,1429 |
0 |
0 |
0 |
19 |
 |
-2,1429 |
0 |
0,1429 |
1 |
0 |
0 |
0 |
0 |
0 |
-0,1429 |
0 |
0 |
0 |
5 |
- |
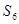 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
6 |
6 |
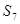 |
-0,1429 |
0 |
0,1429 |
0 |
0 |
0 |
0 |
0 |
1 |
-0,1429 |
0 |
0 |
0 |
6 |
- |
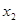 |
0,1429 |
1 |
-0,1429 |
0 |
0 |
0 |
0 |
0 |
0 |
0,1429 |
0 |
0 |
0 |
1 |
7 |
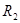 |
1,2857 |
0 |
0,7143 |
0 |
-1 |
0 |
0 |
0 |
0 |
-0,7143 |
1 |
0 |
0 |
5 |
3,8889 |
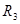 |
4,7143 |
0 |
0,2857 |
0 |
0 |
-1 |
0 |
0 |
0 |
-0,2857 |
0 |
1 |
0 |
8 |
1,697 |
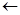 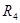 |
6,8571 |
0 |
0,1429 |
0 |
0 |
0 |
-1 |
0 |
0 |
-0,1429 |
0 |
0 |
1 |
6 |
0,875 |
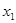 - ведущий столбец - ведущий столбец
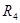 - ведущая строка - ведущая строка
Итерация 2
| Базис
|
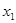 |
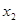 |

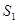
|
 |
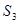 |
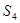 |
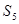 |
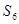 |
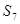 |
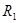 |
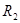 |
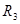 |
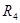 |
Решение
|
Оценка
|
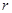 |
0 |
0 |
0,875 |
0 |
-1 |
-1 |
0,875 |
0 |
0 |
-1,875 |
0 |
0 |
-1,875 |
7,75 |
 |
0 |
0 |
0,1875 |
1 |
0 |
0 |
-0,3125 |
0 |
0 |
-0,1875 |
0 |
0 |
0,3125 |
6,875 |
36,6667 |
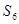 |
0 |
0 |
-0,0208 |
0 |
0 |
0 |
0,1458 |
1 |
0 |
0,0208 |
0 |
0 |
-0,1458 |
5,125 |
- |
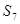 |
0 |
0 |
0,1458 |
0 |
0 |
0 |
-0,0208 |
0 |
1 |
-0,1458 |
0 |
0 |
0,0208 |
6,125 |
42 |
 |
0 |
1 |
-0,1458 |
0 |
0 |
0 |
0,0208 |
0 |
0 |
0,1458 |
0 |
0 |
-0,0208 |
0,875 |
- |
  |
0 |
0 |
0,6875 |
0 |
-1 |
0 |
0,1875 |
0 |
0 |
-0,6875 |
1 |
0 |
-0,1875 |
3,875 |
5,6364 |
 |
0 |
0 |
0,1875 |
0 |
0 |
-1 |
0,6875 |
0 |
0 |
-0,1875 |
0 |
1 |
-0,6875 |
3,875 |
20,6666 |
 |
1 |
0 |
0,0208 |
0 |
0 |
0 |
-0,1458 |
0 |
0 |
-0,0208 |
0 |
0 |
0,1458 |
0,875 |
42 |
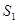 - ведущий столбец - ведущий столбец
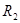 - ведущая строка - ведущая строка
Итерация 3
Базис
|
 |
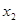 |
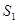 |
 |
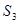 |
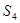 |

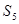
|
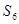 |
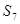 |
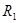 |
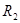 |
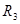 |
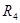 |
Решение
|
Оценка
|
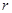 |
0 |
0 |
0 |
0 |
0,2727 |
-1 |
0,6364 |
0 |
0 |
-1 |
-1,2727 |
0 |
-1,6364 |
2,8182 |
 |
0 |
0 |
0 |
1 |
0,2727 |
0 |
-0,3636 |
0 |
0 |
0 |
-0,2727 |
0 |
0,3636 |
5,8182 |
- |
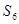 |
0 |
0 |
0 |
0 |
-0,0303 |
0 |
0,1515 |
1 |
0 |
0 |
0,0303 |
0 |
-0,1515 |
5,2422 |
34,6009 |
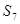 |
0 |
0 |
0 |
0 |
0,2121 |
0 |
-0,0606 |
0 |
1 |
0 |
-0,2121 |
0 |
0,0606 |
5,3033 |
- |
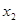 |
0 |
1 |
0 |
0 |
-0,2121 |
0 |
0,0606 |
0 |
0 |
0 |
0,2121 |
0 |
-0,0606 |
1,6967 |
27,9978 |
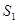 |
0 |
0 |
1 |
0 |
-1,4545 |
0 |
0,2727 |
0 |
0 |
-1 |
1,4545 |
0 |
-0,2727 |
5,6364 |
20,6670 |
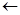 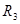 |
0 |
0 |
0 |
0 |
0,2727 |
-1 |
0,6364 |
0 |
0 |
0 |
-0,2727 |
1 |
-0,6364 |
2,8182 |
4,4285 |
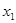 |
1 |
0 |
0 |
0 |
0,0303 |
0 |
-0,1515 |
0 |
0 |
0 |
-0,0303 |
0 |
0,1515 |
0,7578 |
- |
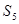 - ведущий столбец - ведущий столбец
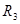 - ведущая строка - ведущая строка
Итерация 4
Базис
|
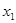 |
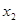 |
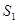 |
 |
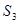 |
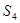 |
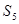 |
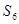 |
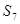 |
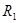 |
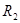 |
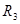 |
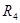 |
Решение
|
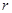 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
-1 |
-1 |
0 |
 |
0 |
0 |
0 |
1 |
0,4285 |
-0,5713 |
0 |
0 |
0 |
0 |
-0,4285 |
0,5713 |
0 |
7,4283 |
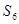 |
0 |
0 |
0 |
0 |
-0,0952 |
0,2381 |
0 |
1 |
0 |
0 |
0,0952 |
-0,2381 |
0 |
4,5714 |
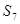 |
0 |
0 |
0 |
0 |
0,238 |
-0,0952 |
0 |
0 |
1 |
0 |
-0,238 |
0,0952 |
0 |
5,5716 |
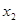 |
0 |
1 |
0 |
0 |
-0,238 |
0,0952 |
0 |
0 |
0 |
0 |
0,238 |
-0,0952 |
0 |
1,4284 |
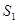 |
0 |
0 |
1 |
0 |
-1,5714 |
0,4285 |
0 |
0 |
0 |
-1 |
1,5714 |
-0,4285 |
0 |
4,4288 |
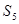 |
0 |
0 |
0 |
0 |
0,4285 |
-1,5713 |
1 |
0 |
0 |
0 |
-0,4285 |
1,5713 |
-1 |
4,4283 |
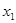 |
1 |
0 |
0 |
0 |
0,0952 |
-0,2381 |
0 |
0 |
0 |
0 |
-0,0952 |
0,2381 |
0 |
1,4286 |
Полученная симплекс-таблица удовлетворяет условиям оптимальности и допустимости.
Переходим на на 2 этап двухэтапного метода
Полученное на этапе I решение используется в качестве начального базиса на этапе II. Далее задача решается обычным симплекс-методом.
Базис
|
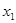 |
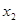 |
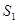 |
 |

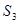
|
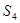 |
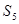 |
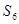 |
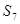 |
Решение
|
Оценка
|
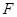 |
0 |
0 |
0 |
0 |
-0,238 |
1,0953 |
0 |
0 |
0 |
3,6508 |
 |
0 |
0 |
0 |
1 |
0,4285 |
-0,5713 |
0 |
0 |
0 |
7,4283 |
17,3356 |
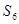 |
0 |
0 |
0 |
0 |
-0,0952 |
0,2381 |
0 |
1 |
0 |
4,5714 |
- |
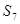 |
0 |
0 |
0 |
0 |
0,238 |
-0,0952 |
0 |
0 |
1 |
5,5716 |
23,4101 |
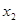 |
0 |
1 |
0 |
0 |
-0,238 |
0,0952 |
0 |
0 |
0 |
1,4284 |
- |
 |
0 |
0 |
1 |
0 |
-1,5714 |
0,4285 |
0 |
0 |
0 |
4,4288 |
- |
  |
0 |
0 |
0 |
0 |
0,4285 |
-1,5713 |
1 |
0 |
0 |
4,4283 |
10,3344 |
 |
1 |
0 |
0 |
0 |
0,0952 |
-0,2381 |
0 |
0 |
0 |
1,4286 |
15,0063 |
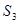 - ведущий столбец - ведущий столбец
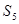 - ведущая строка - ведущая строка
Базис
|
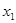 |
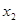 |
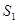 |
 |
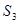 |
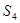 |
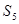 |
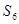 |
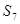 |
Решение
|
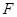 |
0 |
0 |
0 |
0 |
0 |
0,2226 |
0,5554 |
0 |
0 |
6,1110 |
 |
0 |
0 |
0 |
1 |
0 |
1 |
-1 |
0 |
0 |
3 |
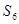 |
0 |
0 |
0 |
0 |
0 |
-0,111 |
0,2222 |
1 |
0 |
5,5552 |
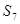 |
0 |
0 |
0 |
0 |
0 |
0,7775 |
-0,5554 |
0 |
1 |
3,112 |
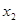 |
0 |
1 |
0 |
0 |
0 |
-0,7511 |
0,5386 |
0 |
0 |
3,8889 |
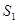 |
0 |
0 |
1 |
0 |
0 |
-5,3338 |
3,6672 |
0 |
0 |
20,6683 |
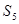 |
0 |
0 |
0 |
0 |
1 |
-3,667 |
2,3337 |
0 |
0 |
10,3344 |
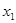 |
1 |
0 |
0 |
0 |
0 |
0,111 |
-0,2222 |
0 |
0 |
0,4445 |
Таким образом, оптимальное решение задачи имеет вид:
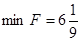 , Х = { , Х = { 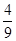 , , 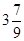 } }
|