Задание на курсовую работу
1. Построить вариационный ряд
2. Рассчитать числовые характеристики статистического ряда:
а) Размах варьирования.
б) Среднее арифметическое значение.
в) Оценки дисперсии.
г) Оценки среднеквадратического отклонения.
д) Мода.
е) Медиана.
ж) Коэффициент вариации.
3. Построить полигон и гистограмму относительных частот.
4. Построить эмпирическую функцию распределения.
5. Построить статистическую проверку гипотезы по нормальному распределению с помощью критерии Пирсона или Колмогорова.
6. Вычислить асимметрию и эксцесс.
7. Построить доверительные интервалы, для математического ожидания и среднеквадратического отклонения для надежности 95%.
8. Выводы.
Данные по выборке вариант 34
| -678 |
-752 |
-624 |
-727 |
-612 |
-632 |
-704 |
-697 |
-627 |
-727 |
| -561 |
-748 |
-686 |
-676 |
-676 |
-696 |
-717 |
-694 |
-700 |
-707 |
| -680 |
-681 |
-687 |
-656 |
-692 |
-644 |
-805 |
-758 |
-695 |
-722 |
| -706 |
-704 |
-681 |
-608 |
-647 |
-699 |
-658 |
-686 |
-689 |
-643 |
| -701 |
-716 |
-731 |
-623 |
-693 |
-703 |
-731 |
-700 |
-765 |
-697 |
| -662 |
-705 |
-667 |
-677 |
-701 |
-678 |
-667 |
-673 |
-697 |
-701 |
| -597 |
-716 |
-689 |
-694 |
-695 |
-729 |
-700 |
-717 |
-647 |
-673 |
| -690 |
-578 |
-703 |
-688 |
-666 |
-670 |
-671 |
-693 |
-688 |
-646 |
| -667 |
-689 |
-711 |
-731 |
-604 |
-691 |
-675 |
-686 |
-670 |
-703 |
| -696 |
-702 |
-660 |
-662 |
-681 |
-666 |
-677 |
-645 |
-746 |
-685 |
1. Построение вариационного ранжированного ряда
Сортируем экспериментальные данные по возрастанию. Получаем вариационный ряд.
Таблица 1
| -805 |
-727 |
-705 |
-700 |
-695 |
-689 |
-681 |
-673 |
-662 |
-632 |
| -765 |
-727 |
-704 |
-700 |
-694 |
-688 |
-680 |
-671 |
-660 |
-627 |
| -758 |
-722 |
-704 |
-700 |
-694 |
-688 |
-678 |
-670 |
-658 |
-624 |
| -752 |
-717 |
-703 |
-699 |
-693 |
-687 |
-678 |
-670 |
-656 |
-623 |
| -748 |
-717 |
-703 |
-697 |
-693 |
-686 |
-677 |
-667 |
-647 |
-612 |
| -746 |
-716 |
-703 |
-697 |
-692 |
-686 |
-677 |
-667 |
-647 |
-608 |
| -731 |
-716 |
-702 |
-697 |
-691 |
-686 |
-676 |
-667 |
-646 |
-604 |
| -731 |
-711 |
-701 |
-696 |
-690 |
-685 |
-676 |
-666 |
-645 |
-597 |
| -731 |
-707 |
-701 |
-696 |
-689 |
-681 |
-675 |
-666 |
-644 |
-578 |
| -729 |
-706 |
-701 |
-695 |
-689 |
-681 |
-673 |
-662 |
-643 |
-561 |
Вывод: Вариационный ряд послужит нам для облегчения дальнейших расчетов, и для определения относительных частот и разделения на интервалы и расчета ряда числовых характеристик.
2. Расчет числовых характеристик статистического ряда
2.1 Размах варьирования
Размах варьирования вычисляется по формуле:
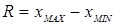 (2.1) (2.1)
где R
– размах варьирования;
x
max
– максимальный элемент вариационного ряда;
xmin
– минимальный элемент вариационного ряда;
x
max
=
– 561
xmin
= -805
R
= -561+805=244
2.2 Среднеарифметическое значение статистического ряда

 (2.2) (2.2)
где ni
– частота варианты xi
;
xi
– варианта выборки;
n = ∑ ni
– объем выборки;
Распределение выборки представлено в таблице 2.
Таблица 2
| Xi |
n |
Xi |
n |
Xi |
n |
Xi |
n |
Xi |
n |
Xi |
n |
Xi |
n |
| -805 |
1 |
-717 |
2 |
-700 |
3 |
-689 |
3 |
-675 |
1 |
-647 |
2 |
-608 |
1 |
| -765 |
1 |
-716 |
2 |
-699 |
1 |
-688 |
2 |
-673 |
2 |
-646 |
1 |
-604 |
1 |
| -758 |
1 |
-711 |
1 |
-697 |
3 |
-687 |
1 |
-671 |
1 |
-645 |
1 |
-597 |
1 |
| -752 |
1 |
-707 |
1 |
-696 |
2 |
-686 |
3 |
-670 |
2 |
-644 |
1 |
-578 |
1 |
| -748 |
1 |
-706 |
1 |
-695 |
2 |
-685 |
1 |
-667 |
3 |
-643 |
1 |
-561 |
1 |
| -746 |
1 |
-705 |
1 |
-694 |
2 |
-681 |
3 |
-666 |
2 |
-632 |
1 |
| -731 |
3 |
-704 |
2 |
-693 |
2 |
-680 |
1 |
-662 |
2 |
-627 |
1 |
| -729 |
1 |
-703 |
3 |
-692 |
1 |
-678 |
2 |
-660 |
1 |
-624 |
1 |
| -727 |
2 |
-702 |
1 |
-691 |
1 |
-677 |
2 |
-658 |
1 |
-623 |
1 |
| -722 |
1 |
-701 |
3 |
-690 |
1 |
-676 |
2 |
-656 |
1 |
-612 |
1 |

2.3 Оценка дисперсии
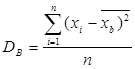
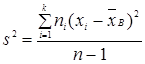 (2.3) (2.3)
где s2
– несмещенная оценка генеральной дисперсии;


2.4 Оценка среднего квадратического отклонения
 (2.4) (2.4)
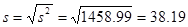
2.5 Определение моды
Модой называют варианту с наибольшей частотой повторений.
Из таблицы 2 находим, что наибольшую частоту n
=3имеют варианты x
= -731, x
= -703,x
= -701,x
= -700,x
= -697, x
= -689,x
= -686, x
= -681, x
= -667.
2.6 Определение медианы
Если количество вариант число четное, то медиана вычисляется по формуле:
МВ
=(
xk
+
xk
+1
)/2
(2.5.)
где xk
– пятидесятый член вариационного ряда;
x
k+1
– пятьдесят первый член вариационного ряда;
n
–
Количество вариант и n
=2*
k
МВ
=(
xk
+
xk
+1
)/2=(-689–689)/2= -689
2.7 Расчет коэффициента вариации
Расчет коэффициента вариации проведем по формуле:
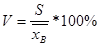 (2.6)
(2.6)

Вывод:
Размах варьирования является простейшей характеристикой рассеяния вариационного ряда.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводные характеристики – генеральную дисперсию и средним квадратическим отклонением.
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние, у которого коэффициент больше (эта величина безразмерная поэтому он пригоден для сравнения вариационных рядов, варианты которых имеют различную размерность.
В целом числовые характеристики служат для сравнения рассеяния вариационных рядов в сравнении с аналогичными числовыми характеристиками других вариационных рядов.
3. Построение полигона и гистограммы относительных частот
Для построения гистограммы и полигона относительных частот поделим вариационный ряд (табл. 1) на частичные интервалы. Результаты занесем в таблицу 3.
Таблица 3
Номер интервала
I
|
Частичный интервал xi
–xx
+1
|
Сумма относительных частот
wi
|
Плотность частот

|
| xi
|
xx
+1
|
| 1 |
-805 |
-780,6 |
0,01 |
0,00041 |
| 2 |
-780,6 |
-756,2 |
0,02 |
0,00082 |
| 3 |
-756,2 |
-731,8 |
0,03 |
0,00123 |
| 4 |
-731,8 |
-707,4 |
0,12 |
0,00492 |
| 5 |
-707,4 |
-683 |
0,4 |
0,01639 |
| 6 |
-683 |
-658,6 |
0,24 |
0,00984 |
| 7 |
-658,6 |
-634,2 |
0,08 |
0,00328 |
| 8 |
-634,2 |
-609,8 |
0,05 |
0,00205 |
| 9 |
-609,8 |
-585,4 |
0,03 |
0,00123 |
| 10 |
-585,4 |
-561 |
0,02 |
0,00082 |
По таб. 3 строим гистограмму относительных частот (рис. 1).
Полигон получаем соединением вершин столбцов гистограммы. (рис. 1) Полигон получаем соединением вершин столбцов гистограммы.
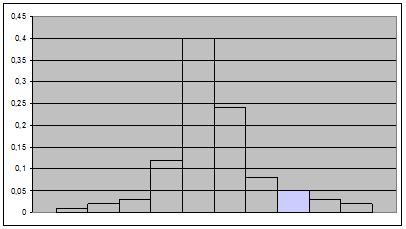
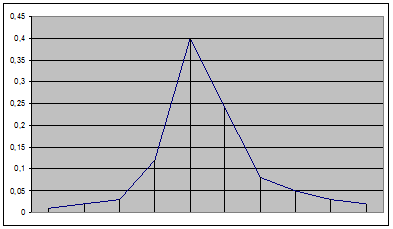
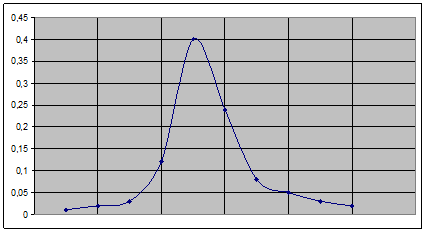
Рис 1.
Вывод: Полигон и гистограмму – графики статистического распределения строят для наглядности относительных частот в выборке.
4. Построение эмпирической функции распределения
Эмпирическая функция распределения выборки находится по формуле:
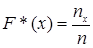 (4.1) (4.1)
где nx
– число вариант меньших х
;
n
–
объем выборки.
По формуле (4.1) построим эмпирическую функцию распределения.
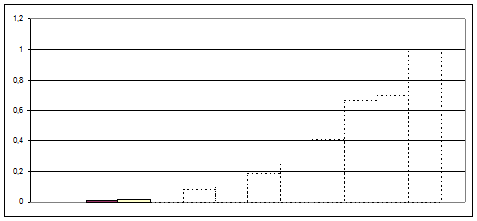
Для более точного и правильного построения возьмем середины интервалов:
| F(x) |
Интервал |
| 0 |
X< |
-792,8 |
| 0,01 |
-792,8 |
<x< |
-768,4 |
| 0,02 |
-768,4 |
<x< |
-744 |
| 0,03 |
-744 |
<x< |
-719,6 |
| 0,05 |
-719,6 |
<x< |
-695,2 |
| 0,08 |
-695,2 |
<x< |
-670,8 |
| 0,12 |
-670,8 |
<x< |
-646,4 |
| 0,19 |
-646,4 |
<x< |
-622 |
| 0,27 |
-622 |
<x< |
-597,6 |
| 0,41 |
-597,6 |
<x< |
-573,2 |
| 0,67 |
-573,2 |
<x< |
-548,8 |
| 1 |
x> |
-548,8 |
Вывод:
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности
5. Статистическая проверка гипотезы о нормальном распределении с помощью критерия Пирсона или Колмагорова
Проверку проводим с помощью критерия Пирсона.
В этом задании, с помощью критерии Пирсона проверим гипотезу о нормальном распределении генеральной совокупности, с этой целью будем сравнивать эмпирические и теоретические частоты.
 – Среднее арифметическое значение – Среднее арифметическое значение
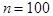 – Количество вариантов – Количество вариантов
 – Шаг интервалов – Шаг интервалов
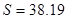 – Оценка среднеквадратического отклонения. – Оценка среднеквадратического отклонения.

Вычислим данные по таблице:
| I |
ni |
Xi |
X (i+1) |
Zi |
Z (I+1) |
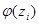 |

|
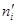 |
 |
 |
| 1 |
1 |
-805 |
-780,6 |
-2,7340 |
-0,5 |
-0,469 |
3,1 |
1,4226 |
0,3226 |
| 2 |
1 |
-780,6 |
-756,2 |
-2,7340 |
-2,1140 |
-0,469 |
-0,408 |
6,1 |
4,2639 |
0,1639 |
| 3 |
4 |
-756,2 |
-731,8 |
-2,1140 |
-1,4941 |
-0,408 |
-0,285 |
12,3 |
5,6008 |
1,3008 |
| 4 |
7 |
-731,8 |
-707,4 |
-1,4941 |
-0,8741 |
-0,285 |
-0,099 |
18,6 |
7,2344 |
2,6344 |
| 5 |
26 |
-707,4 |
-683 |
-0,8741 |
-0,2542 |
-0,099 |
0,1141 |
21,31 |
1,0322 |
31,7222 |
| 6 |
33 |
-683 |
-658,6 |
-0,2542 |
0,3658 |
0,1141 |
0,2939 |
17,98 |
12,5473 |
60,5673 |
| 7 |
14 |
-658,6 |
-634,2 |
0,3658 |
0,9857 |
0,2939 |
0,4131 |
11,92 |
0,3630 |
16,4430 |
| 8 |
8 |
-634,2 |
-609,8 |
0,9857 |
1,6057 |
0,4131 |
0,4713 |
5,82 |
0,8166 |
10,9966 |
| 9 |
3 |
-609,8 |
-585,4 |
1,6057 |
2,2256 |
0,4713 |
0,4927 |
2,14 |
0,3456 |
4,2056 |
| 10 |
3 |
-585,4 |
-561 |
2,2256 |
0,4927 |
0,5 |
0,73 |
7,0588 |
12,3288 |
| СУММА |
100 |
100 |
40,6851 |
140,6851 |
X2
набл
=40,685
Контроль: 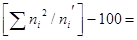 140,685–100=40,685 140,685–100=40,685
Исходя из требований, чтобы вероятность попадания критерия в критическую область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости 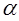 . .

Таким образом, правосторонняя критическая область определяется неравенством  , а область принятия нулевой гипотезы – неравенством , а область принятия нулевой гипотезы – неравенством . .
Уровень значимости 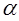 = 0,05; = 0,05;
По таблице критических точек распределения χ² (приложение 3), по уровню значимости α = 0,05 и числу степеней свободы K=10–3=7 находим критическую точку правосторонней критической области χ²кр (0,05; 7) = 14,1.
Вывод: Так как X2
набл
> X2
кр,
то нулевую гипотезу отвергают, значит гипотезу о нормальном распределении отвергают.
6. Расчет асимметрии и эксцесса
Асимметрия – отношение центрального момента 3-го порядка к кубу среднего квадратического отклонения.
 , где , где 
Эксцесс – характеристика «крутости» рассматриваемой случайной величины.
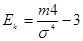 , где , где 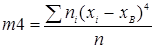
Значение ХВ,
s вычисляем по формулам:
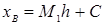 , ,
где С – Ложный нуль (варианта, которая имеет наибольшую частоту).
 , ,
где h – шаг (разность между двумя соседними вариантами);
 (условный момент второго порядка); (условный момент второго порядка);
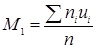 (условный момент первого порядка); (условный момент первого порядка);
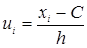 (условная варианта). (условная варианта).
Расчеты занесем в таблицу 7:
| Xi
|
Ni
|
Ui
|
XB
|
M1
|
M2
|
s |
m3 |
m4 |
AS
|
EK
|
| -805 |
1 |
-2,73 |
-684,67 |
0,30 |
1,06 |
23,97 |
3433,28 |
4193007,72 |
0,25 |
12,71 |
| -780,6 |
1 |
-2,11 |
| -756,2 |
4 |
-1,49 |
| -731,8 |
7 |
-0,87 |
| -707,4 |
26 |
-0,25 |
| -683 |
33 |
0,37 |
| -658,6 |
14 |
0,99 |
| -634,2 |
8 |
1,61 |
| -609,8 |
3 |
2,23 |
| -585,4 |
3 |
2,85 |
Вывод:
Т.к. асимметрия положительна то ‘длинная часть’ кривой распределения расположена справа от математического ожидания или мода.
Т.к. Эксцесс больше нуля, то кривая распределения имеет более высокую и ‘острую’ вершину, чем нормальная кривая.
7. Построение доверительного интервала для математического ожидания и среднего квадратического отклонения
Доверительный интервал для математического ожидания (с вероятностью g) находят как:
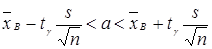 (7.1) (7.1)
где n
– объем выборки;
t
g
– случайная величина имеющее распределение Стьюдента находим по приложению 1.
s – исправленное среднее квадратическое отклонение;
 – выборочное среднее;
– выборочное среднее;
Найдем интервал:
по приложению 1 находим t
g
= 1.984
при g
=
0.95
и n
= 100
;
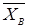 =-684,67;
s
=
38,19
; =-684,67;
s
=
38,19
;
Получаем
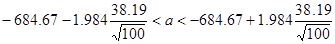
-692,25<a<-677.09
Доверительный интервал для среднего квадратического отклонения
(с надежностью g) находят как:
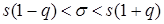 при q
<1 (7.2) при q
<1 (7.2)
 при q
>1 (7.3) при q
>1 (7.3)
где q находят по приложению 2, по заданным n
и g
;
Исходя из приложения 2, n = 100 и g
= 0.95 находим q
=0.143;
Поэтому интервал находим по формуле (7.2):
38.19(1-0.143)<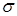 <38.19(1+0.143) 35,58(1+0.143) <38.19(1+0.143) 35,58(1+0.143) |
|
32.73 <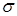 < 43.65 < 43.65
Вывод:
Итак, с надежностью 0,95 неизвестное математическое ожидание ‘а’ находится в доверительном интервале -692,25<a<-677.09, а неизвестное среднее квадратическое отклонение ‘
’ находиться в доверительном интервале 32.73 <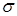 < 43.65. < 43.65.
Вывод
Для представления генеральной совокупности я исследовала выборку, которая имеет объём 100 элементов.
Я нашла:
размах варьирования R
=
244;
среднеарифметическое значение статистического ряда  =-684,67; =-684,67;
несмещенную оценку генеральной дисперсии s
2
=
1458,99;
среднее квадратическое отклонение s
=
38,19;
медиану МВ
=
-689 и коэффициент вариации V=
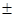 5,58%.
5,58%.
С надежностью 0.95 оценил математическое ожидание в интервале
-692,25<а
< -677,09
и среднее квадратическое отклонение в интервале
32,73 <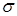 < 43,65 < 43,65
Выборка имеет варианты x
= -731, x
= -703,x
= -701,x
= -700,x
= -697, x
= -689,x
= -686, x
= -681, x
= -667, которые встречаются 3 раза.
На рис. 1 построила гистограмму и полигон относительных частот. По рис. 1 можно выдвинуть гипотезу о нормальном распределении генеральной совокупности.
После проверки гипотезы о нормальном распределении с помощью критерия Пирсона при a=0.05, я отвергла ее. Из этого следует, что расхождения между практическими и теоретическими частотами значимо.
Асимметрия as
=0,25. Из этого следует, что правое крыло функции более вытянуто относительно ее моды.
Эксцесс ek
=12,71. Из-за того, что у эксцесса положительный знак, эмпирическая функция распределения острее по сравнению с теоретическим распределением.
Список литературы
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2001.
2. Гмурман В.Е. Теория вероятностей и математическая статистика.
М.: Высшая школа, 2001.
|