 Распределение электрического поля и потенциала
Чтобы рассчитать распределение электрического потенциала в месте контакта, необходимо решитьуравнение Пуассона. Для одного измерения оно выглядит следующим образом:
 φ(х) – распределение потенциала,  - объёмная плотность электрического заряда, ε – диэлектрическая проницаемость. В самом общем случае  определяется суммой всех зарядов, которые существуют в материале, т.е.  . Разные знаки связаны с разным зарядом. При комнатной температуре примеси полностью ионизированы, и значения  и  (концентрации ионизированных примесей) равны  и  . С концентрацией носителей заряда оказывается сложнее поскольку она меняется на протяжении p-n перехода. В первом приближении можно считать, что в p-n переходе нет носителей заряда (обеднённый слой). Как показывают численные расчёты, это приближение оказывается достаточно точным, поскольку изменение концентрации электронов и дырок на протяжении p-n перехода изменяется как минимум на порядок. И только на границах p-n перехода приближение оказывается не точным, поскольку концентрация – плавная функция и не имеет разрывов. Однако размеры этих приграничных слоёв очень малы, намного меньше реальных размеров p-n перехода. Следовательно, в области p-n перехода объёмная плотность заряда определяется только распределением примеси  , которое в общем случае представляет собой произвольную кривую. Однако тогда невозможно решить аналитически уравнение Пуассона. Даже если взять экспоненциальную зависимость концентрации примеси (приближённое описание процесса диффузии), решение оказывается настолько сложным, что теряет всякий смысл. Поэтому резонно разложить кривую распределения примеси в ряд Тейлора и искать приближенное решение. Плавный p-n перехода Первое приближение даёт линейное распределение примеси (рис. 1). Такое приближение достаточно хорошо описывает некоторые диффузионные p-n переходы и переходы коллектор-база в биполярных приборах. P-n переход в этом случае называется плавным. Объёмный заряд линейно зависит от х и определяется   где a –градиент концентрации примеси, т.е. первая производная кривой распределения примеси в точке металлургического контакта. Тогда первое интегрирование даст следующий результат:  Здесь  - постоянная величина, которая появляется при интегрировании. Для определения этой величины следует ввести граничные условия. Известно, что напряжённость электрического поля определяется как Рис. 1  , следовательно, мы получили распределение напряжённости электрического поля вдоль оси x, взятое с обратным знаком. Если считать, что проводимость полупроводников в объёме намного больше проводимости слоя объёмного заряда, то всё электрическое поле сосредоточено в слое объёмного заряда, а в объёме полупроводников оно равно нулю. Следовательно, для  и   . Тогда  для  ,  для  и  ,  . Второе интегрирование позволяет получить распределение потенциала вдоль оси x:
 Обозначим  и  потенциалы n- и р- областей соответственно, тогда
 и
Как и для предыдущего решения, при x=0 значения функции и её производной должны быть одинаковыми для обеих формул, т.е.  и  (1) Отсюда следует, что в отличие от резкого, плавный р-n переход всегда симметричный и  , а разность потенциалов n- и р- областей равна:  И тогда толщина плавного р-n перехода:
 (2) Барьерная ёмкость. По определению, ёмкость – скорость изменения заряда при изменении приложенного напряжения, т.е.  . Изменение заряда в переходе связано с изменением толщины области обеднения, которая зависит от приложенного напряжения. Рассчитаем ёмкость для плавного р-n перехода. Задание 1 Ёмкость плавного р-n перехода. Исходя из рис. 1 и соотношения (1) получаем изменение заряда: 
а изменение напряжения – из (2)  И опять барьерная ёмкость определяется по формуле плоского конденсатора  Получившийся одинаковый результат не случайность, а следствие связи между зарядом и потенциалом через уравнение Пуассона, и полученную формулу для ёмкости вообще-то можно доказать для любого распределения примеси. Хотя следует отметить различие между плоским конденсатором и р-n переходом: изменение заряда в конденсаторе происходит за счёт изменения плотности заряда при неизменном расстоянии между обкладками, а в р-n переходе – за счёт изменения области, занимаемой зарядом при неизменной его плотности. Исходя из получившийся формулы для барьерной ёмкости следует, что последняя будет зависеть от приложенного напряжения, поскольку от него зависит толщина области объёмного заряда. При прямых напряжениях больших, чем  исчезает само понятие барьерной ёмкости, поскольку исчезает область объёмного заряда .
Задание 2 Рассчитать величину барьерной ёмкости плавного р-n перехода при 300 К и прямом напряжении  Дано:   
T = 300 K 
Т.к. примеси полностью истощены и собственная проводимость ещё очень мала, то можно предположить:  ;  Контактная разность потенциалов 
 (В)
Барьерная ёмкость 
 Распределение электрического поля и потенциала
Чтобы рассчитать распределение электрического потенциала в месте контакта, необходимо решитьуравнение Пуассона. Для одного измерения оно выглядит следующим образом:
 φ(х) – распределение потенциала,  - объёмная плотность электрического заряда, ε – диэлектрическая проницаемость. В самом общем случае  определяется суммой всех зарядов, которые существуют в материале, т.е.  . Разные знаки связаны с разным зарядом. При комнатной температуре примеси полностью ионизированы, и значения  и  (концентрации ионизированных примесей) равны  и  . С концентрацией носителей заряда оказывается сложнее поскольку она меняется на протяжении p-n перехода. В первом приближении можно считать, что в p-n переходе нет носителей заряда (обеднённый слой). Как показывают численные расчёты, это приближение оказывается достаточно точным, поскольку изменение концентрации электронов и дырок на протяжении p-n перехода изменяется как минимум на порядок. И только на границах p-n перехода приближение оказывается не точным, поскольку концентрация – плавная функция и не имеет разрывов. Однако размеры этих приграничных слоёв очень малы, намного меньше реальных размеров p-n перехода. Следовательно, в области p-n перехода объёмная плотность заряда определяется только распределением примеси  , которое в общем случае представляет собой произвольную кривую. Однако тогда невозможно решить аналитически уравнение Пуассона. Даже если взять экспоненциальную зависимость концентрации примеси (приближённое описание процесса диффузии), решение оказывается настолько сложным, что теряет всякий смысл. Поэтому резонно разложить кривую распределения примеси в рад Тейлора и искать приближенное решение. Плавный p-n перехода Первое приближение даёт линейное распределение примеси (рис. 1). Такое приближение достаточно хорошо описывает некоторые диффузионные p-n переходы и переходы коллектор-база в биполярных приборах. P-n переход в этом случае называется плавным. Объёмный заряд линейно зависит от х и определяется  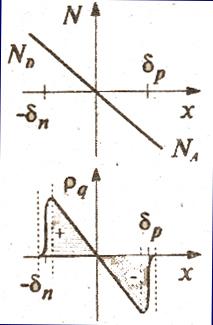 где a –градиент концентрации примеси, т.е. первая производная кривой распределения примеси в точке металлургического контакта. Тогда первое интегрирование даст следующий результат:  Здесь  - постоянная величина, которая появляется при интегрировании. Для определения этой величины следует ввести граничные условия. Известно, что напряжённость электрического поля определяется как Рис. 1  , следовательно, мы получили распределение напряжённости электрического поля вдоль оси x, взятое с обратным знаком. Если считать, что проводимость полупроводников в объёме намного больше проводимости слоя объёмного заряда, то всё электрическое поле сосредоточено в слое объёмного заряда, а в объёме полупроводников оно равно нулю. Следовательно, для  и   . Тогда  для  ,  для  и  ,  . Второе интегрирование позволяет получить распределение потенциала вдоль оси x:
 Обозначим  и  потенциалы n- и р- областей соответственно, тогда
 и
Как и для предыдущего решения, при x=0 значения функции и её производной должны быть одинаковыми для обеих формул, т.е.  и  Отсюда следует, что в отличие от резкого, плавный р-n переход всегда симметричный и  , а разность потенциалов n- и р- областей равна:  И тогда толщина плавного р-n перехода:
 Распределение электрического поля и потенциала
Чтобы рассчитать распределение электрического потенциала в месте контакта, необходимо решитьуравнение Пуассона. Для одного измерения оно выглядит следующим образом:
 φ(х) – распределение потенциала,  - объёмная плотность электрического заряда, ε – диэлектрическая проницаемость. В самом общем случае  определяется суммой всех зарядов, которые существуют в материале, т.е.  . Разные знаки связаны с разным зарядом. При комнатной температуре примеси полностью ионизированы, и значения  и  (концентрации ионизированных примесей) равны  и  . С концентрацией носителей заряда оказывается сложнее поскольку она меняется на протяжении p-n перехода. В первом приближении можно считать, что в p-n переходе нет носителей заряда (обеднённый слой). Как показывают численные расчёты, это приближение оказывается достаточно точным, поскольку изменение концентрации электронов и дырок на протяжении p-n перехода изменяется как минимум на порядок. И только на границах p-n перехода приближение оказывается не точным, поскольку концентрация – плавная функция и не имеет разрывов. Однако размеры этих приграничных слоёв очень малы, намного меньше реальных размеров p-n перехода. Следовательно, в области p-n перехода объёмная плотность заряда определяется только распределением примеси  , которое в общем случае представляет собой произвольную кривую. Однако тогда невозможно решить аналитически уравнение Пуассона. Даже если взять экспоненциальную зависимость концентрации примеси (приближённое описание процесса диффузии), решение оказывается настолько сложным, что теряет всякий смысл. Поэтому резонно разложить кривую распределения примеси в ряд Тейлора и искать приближенное решение. Плавный p-n перехода Первое приближение даёт линейное распределение примеси (рис. 1). Такое приближение достаточно хорошо описывает некоторые диффузионные p-n переходы и переходы коллектор-база в биполярных приборах. P-n переход в этом случае называется плавным. Объёмный заряд линейно зависит от х и определяется  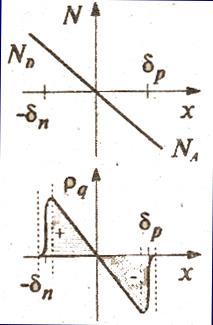 где a –градиент концентрации примеси, т.е. первая производная кривой распределения примеси в точке металлургического контакта. Тогда первое интегрирование даст следующий результат:  Здесь  - постоянная величина, которая появляется при интегрировании. Для определения этой величины следует ввести граничные условия. Известно, что напряжённость электрического поля определяется как Рис. 1  , следовательно, мы получили распределение напряжённости электрического поля вдоль оси x, взятое с обратным знаком. Если считать, что проводимость полупроводников в объёме намного больше проводимости слоя объёмного заряда, то всё электрическое поле сосредоточено в слое объёмного заряда, а в объёме полупроводников оно равно нулю. Следовательно, для  и   . Тогда  для  ,  для  и  ,  . Второе интегрирование позволяет получить распределение потенциала вдоль оси x:
 Обозначим  и  потенциалы n- и р- областей соответственно, тогда
 и
Как и для предыдущего решения, при x=0 значения функции и её производной должны быть одинаковыми для обеих формул, т.е.  и  (1) Отсюда следует, что в отличие от резкого, плавный р-n переход всегда симметричный и  , а разность потенциалов n- и р- областей равна:  И тогда толщина плавного р-n перехода:
 (2) Барьерная ёмкость. По определению, ёмкость – скорость изменения заряда при изменении приложенного напряжения, т.е.  . Изменение заряда в переходе связано с изменением толщины области обеднения, которая зависит от приложенного напряжения. Рассчитаем ёмкость для плавного р-n перехода. Задание №1 Ёмкость плавного р-n перехода. Исходя из рис. 1 и соотношения (1) получаем изменение заряда: 
а изменение напряжения – из (2)  И опять барьерная ёмкость определяется по формуле плоского конденсатора  Получившийся одинаковый результат не случайность, а следствие связи между зарядом и потенциалом через уравнение Пуассона, и полученную формулу для ёмкости вообще-то можно доказать для любого распределения примеси. Хотя следует отметить различие между плоским конденсатором и р-n переходом: изменение заряда в конденсаторе происходит за счёт изменения плотности заряда при неизменном расстоянии между обкладками, а в р-n переходе – за счёт изменения области, занимаемой зарядом при неизменной его плотности. Исходя из получившийся формулы для барьерной ёмкости следует, что последняя будет зависеть от приложенного напряжения, поскольку от него зависит толщина области объёмного заряда. При прямых напряжениях больших, чем  исчезает само понятие барьерной ёмкости, поскольку исчезает область объёмного заряда .
Задание №2 Рассчитать величину барьерной ёмкости плавного р-n перехода при 300 К и прямом напряжении  Дано:   
T = 300 K 
Т.к. примеси полностью истощены и собственная проводимость ещё очень мала, то можно предположить:  ;  Контактная разность потенциалов 
 (В)
Барьерная ёмкость 
Ответ: 167 пФ
Таким образом, при наложении на исследуемый р-n переход напряжения прямого смещения  . Его барьерная ёмкость равна 167 пФ.
Задание №3 Построить график зависимости барьерной ёмкости от температуры.
 ; 
 то  то 
 В
| T | n(T) | 
| 
| 
| | 70 | 
| 
| 
| 160.2 | | 100 | 
| 
| 
| 160.5 | | 150 | 
| 
| 
| 161.43 | | 200 | 
| 
| 
| 162.57 | | 250 | 
| 
| 
| 163.94 | | 300 | 
| 
| 
| 166.5 |
 
  Знак «+» берётся при приложенном обратном напряжении, Знак «-» берётся при приложенном прямого напряжения.  - контактная разность потенциалов.
Литература: С.П. Медведев. Физика полупроводниковых и микроэлектронных приборов (биполярные приборы), учебное пособие. Епифанов, Мома. Физические основы конструирования и технологии РЭА и ЭВА.
Кузнецкий институт информационных и управленческих технологий (филиал ПГУ) Кафедра Микроэлектроники
Курсовая работа По дисциплине: Физические основы микроэлектроники Тема: Ёмкость плавного р-nперехода
Проверил: Абрамов В.Г. Выполнил: студент гр. 02КР1 Кулиш С.В.
г. Кузнецк 2003 г. |
