| Цель работы
1. Изучить методику экспериментального определения кривых разгона объекта управления и определить кривые разгона по каналам регулирования и возмущения для напорного бака.
2. Оценить по кривым разгона важнейшие динамические характеристики объекта управления: чистое транспортное запаздывание, самовыравнивание, емкость, инерционность.
3. Провести математическое описание динамики объекта управления по двум каналам (по каналу возмущения и каналу регулирования поочерёдно) линейным дифференциальным уравнением первого порядка. Определить коэффициенты дифференциального уравнения первого порядка и соответствующей ему передаточной функции первого порядка, вывести уравнение для построения расчётной кривой разгона.
4. Провести математическое описание динамики объекта управления по каналам возмущения и регулирования дифференциальным уравнением второго порядка. Определить коэффициенты дифференциального уравнения второго порядка и соответствующей ему передаточной функции второго порядка, вывести уравнение для построения расчётной кривой разгона.
Изучение кривой разгона первого порядка по каналу регулирования
1. Изучаемый объект: Напорный бак с подогревом.
2. Раздел: Практика Хвоз
=20%, Хрег
=57%
3. Задаем ступенчатое изменение Хрег
=67% (+10%), ждем, когда объект стабилизируется (Хвых
(t)=const).
4. От момента задания возмущения до момента стабилизации по выходному каналу мы наблюдаем кривую разгона.
5. Останавливаем процесс нажатием клавиши “S”, далее “F7”. Задаем оси новой системы координат.
6. Далее на экране отображается выделенный участок, на котором необходимо выявить точку перегиба, обозначить ее и установить касательную.
7. В результате видим на экране расчётную модель кривой разгона первого порядка.
8. Снимаем показания. Соглашаемся с результатом расчетной модели, возвращаемся к окну процесса. Получаем величину k=1,9.
Кривая разгона с обозначениями параметров кривой
Описание объекта управления в динамике можно сделать с помощью дифференциального уравнения второго порядка с запаздыванием следующего вида:
 , при
 (1)
Где k - коэффициент усиления (передачи) рассматриваемого канала объекта
 - время чистого транспортного запаздывания, определение которого также уже было рассмотрено. Коэффициент усиления можно выразить:
 (2)
Рассмотрим точку перегиба. Как известно из математики, в точке перегиба вторая производная равна 0, т.е.
 (3)
 (4) –
это следует из того что тангенс угла найдётся из треугольника, как отношение противолежащего катета хвых уст
=В
к прилежащему, равному Т
Так же справедливо равенство уравнения разгона:
 (5)
или  (6)
Причём  . Тогда из этого уравнения нетрудно получить формулу для коэффициента a1
:
 (7)
Перейдём к определению коэффициента а2
. Для этого предварительно проинтегрируем исходное дифференциальное уравнение второго порядка (1), отбросив в нём на время уже определённое время чистого транспортного запаздывания. Получим:
 (8)
Перепишем это уравнения для точки перегиба с координатами (tп
, xвых
(tп
)):
 . (9)
В уравнении (9):
 (10)
а интеграл выражает площадь под кривой разгона до точки перегиба, поэтому обозначим его так:
 . (11)
С учётом выражений (10) и (11) уравнение (9) примет вид:
 (12)
Из этого уравнения и выведем формулу для определения последнего неизвестного коэффициента а2
, получим:
 . (13)
После определения всех коэффициентов дифференциального уравнения (1), перейдём к соответствующей ему передаточной функции, для чего уравнение (1) предварительно преобразуем по Лапласу, а затем найдём отношение изображения выходной величины объекта к входной (при нулевых начальных условиях), получим:
 . (14)
Помня, что  , а изображение входного ступенчатого сигнала  имеет вид  нетрудно получит изображение выходной величины:
 . (15)
Далее, пользуясь известными из математики методами (например, разлагая правую часть выражения (15) на простые дроби при временном отбрасывании запаздывания, а затем учёте его в полученном выражении путём формальной замены  ), получим уравнение расчётной кривой разгона апериодического объекта второго порядка с запаздыванием:
 , при
 . (16)
По уравнению (16) и проводится проверка точности совпадения расчётной кривой разгона с экспериментальной, т.е. проверка адекватности математической модели объекта. В уравнении (16) p1
и p2
– корни характеристического уравнения объекта по рассматриваемому каналу, получаемого приравниванием знаменателя передаточной функции (14) к нулю, т.е. корни уравнения вида:
 . (17)
Кривая разгона по регулированию
 = 18с, T=
83,61с,  =1,9,  =0,53.
Имея данные, полученные выше, можем изобразить передаточную функцию:
Подставив полученные данные в формулу  при  , получаем расчётное значение xвых
(t).
| t
|
Хвых(t)Практ
|
Хвых(t)Расчет
|
| 0
|
0
|
0
|
| 12
|
0
|
0
|
| 24
|
1,5
|
1,18
|
| 36
|
3,5
|
3,74
|
| 48
|
5,5
|
5,94
|
| 60
|
7,5
|
7,85
|
| 72
|
9
|
9,50
|
| 84
|
10,5
|
10,93
|
| 96
|
12
|
12,16
|
| 108
|
13
|
13,22
|
| 120
|
14
|
14,14
|
| 132
|
14,5
|
14,94
|
| 144
|
15,5
|
15,63
|
| 156
|
16
|
16,22
|
| 168
|
16,5
|
16,73
|
*Значение при t=0 рассчитать не удается т.к. не выполняется условие
Графическое отображение зависимости выходных характристик от времени
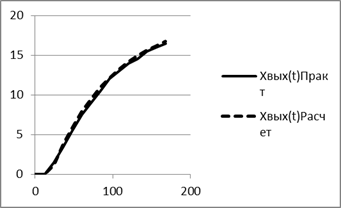
Кривая разгона по возмущению
Задаем ступенчатое возмущение Хаозм
=25% (-5%), ждем, когда объект стабилизируется (Хвых
(t)=const).
= 26,26с, Т=
95,92 с,  =4,4,  =0,23.
Имея данные, полученные выше, можем изобразить передаточную функцию:
Подставив полученные данные в формулу при , получаем расчётное значение xвых
(t).
| t
|
Хвых(t)Практ
|
Хвых(t)Расчет
|
| 0
|
0
|
| 30
|
2
|
1,49
|
| 60
|
6,5
|
6,81
|
| 90
|
11
|
10,76
|
| 120
|
14
|
13,68
|
| 150
|
16
|
15,84
|
| 180
|
17,5
|
17,44
|
| 210
|
19
|
18,62
|
| 240
|
20
|
19,50
|
| 270
|
20,5
|
20,15
|
| 300
|
21
|
20,63
|
| 330
|
21,5
|
20,98
|
| 360
|
21,5
|
21,25
|
| 390
|
22
|
21,44
|
| 420
|
22
|
21,59
|
*Значение при t=0 рассчитать не удается т.к. не выполняется условие 
Графическое отображение зависимости выходных характристик от времени:
Кривая разгона по регулированию второго порядка
Задаем ступенчатое регулирование Хрег
=67% (+10%), ждем, когда объект стабилизируется (Хвых
(t)=const).
Чистое запаздывание τ=21,15с, постоянная времени объекта Т=
100,94с,
 =1,9, =0,53.
Имея данные полученные выше можем изобразить передаточную функцию:
 
Подставим полученные данные в формулу
при условии что t≥τ. Где p1
и p2
корни уравнения 
| t
|
Хвых(t)Практ
|
Хвых(t)Расчет
|
| 0
|
0
|
0*
|
| 12
|
0
|
0*
|
| 24
|
1,5
|
1,32
|
| 36
|
3,5
|
3,94
|
| 48
|
5,5
|
6,11
|
| 60
|
7,5
|
7,97
|
| 72
|
9
|
9,59
|
| 84
|
10,5
|
10,98
|
| 96
|
12
|
12,19
|
| 108
|
13
|
13,24
|
| 120
|
14
|
14,15
|
| 132
|
14,5
|
14,93
|
| 144
|
15,5
|
15,61
|
| 156
|
16
|
16,20
|
| 168
|
16,5
|
16,71
|
*Значение при t=0 рассчитать не удается т.к. не выполняется условие 
Графическое отображение выходных характеристик:
Кривая разгона по возмущению второго порядка
Задаем ступенчатое возмущение Хаозм
=25% (-5%), ждем, когда объект стабилизируется (Хвых
(t)=const).
Чистое запаздывание τ=26,68с, постоянная времени объекта Т=
115,23с,
 =4,4,  =0,23.
Имея данные полученные выше можем изобразить передаточную функцию:
Подставим полученные данные в формулу
при условии что t≥τ. Где p1
и p2
корни уравнения 
| t
|
Хвых(t)Практ
|
Хвых(t)Расчет
|
| 0
|
0
|
0
|
| 30
|
2
|
2,08
|
| 60
|
6,5
|
7,29
|
| 90
|
11
|
11,11
|
| 120
|
14
|
13,93
|
| 150
|
16
|
16,02
|
| 180
|
17,5
|
17,57
|
| 210
|
19
|
18,72
|
| 240
|
20
|
19,57
|
| 270
|
20,5
|
20,20
|
| 300
|
21
|
20,67
|
| 330
|
21,5
|
21,01
|
| 360
|
21,5
|
21,27
|
| 390
|
22
|
21,46
|
| 420
|
22
|
21,60
|
*Значение при t=0 рассчитать не удается т.к. не выполняется условие
Графическое отображение выходных характеристик:
Вывод
В результате проделанной работы мы приобрели навыки определения и анализа (точка перегиба, касательная, площадь под кривой до точки перегиба) кривой разгона при задании ступенчатого сигнала по каналам возмущения и регулирования. Были изображены расчетные кривые разгона первого и второго порядков, выведены передаточные функции из дифференциальных уравнений первого и второго порядка, определены необходимые коэффициенты.
|
