|
Введение
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
-2-
1. Задача Коши для дифференциального уравнения первого порядка
Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0
), удовлетворяющего начальным условиям у(х0
) = у0
.
Теорема Коши
.
(теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную 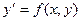 , то какова бы не была точка (х0
, у0
) в области D, существует единственное решение , то какова бы не была точка (х0
, у0
) в области D, существует единственное решение 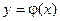 уравнения уравнения 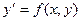 , определенное в некотором интервале, содержащем точку х0
, принимающее при х = х0
значение j(х0
) = у0
, т.е. существует единственное решение дифференциального уравнения. , определенное в некотором интервале, содержащем точку х0
, принимающее при х = х0
значение j(х0
) = у0
, т.е. существует единственное решение дифференциального уравнения.
1.1. Геометрический смысл
Геометрически речь идет о нахождении интегральной кривой, проходящей через заданную точку М (х ,у ).
Исключительно большое значение для теории дифференциальных уравнений и ее приложений имеет вопрос о существенности решения задачи Коши и о единственности этого решения. Будем говорить, что задача Коши
имеет единственное решение, если можно указать такую окрестность точки х
|х – x |<h (1.2)
что в ней определено решение (1.1) и не существует решения
у=у (х,х ,у ),
определенного в той же окрестности (1.2), значение которого не совпадает со значениями решения (1.1) хоть в одной точке окрестности (1.2), отличной от точки х . В противном случае говорят, что единственность решения задачи Коши нарушена.
Наличие свойства единственности зависит от дифференциального уравнения и от началиных данных х ,у .
1.2. Механический смысл
-3-
2. Общее и частное решение дифференциального уравнения первого порядка
Общим решением
дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
Свойства общего решения:
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0
, у(х0
) = у0
существует такое значение С = С0
, при котором решением дифференциального уравнения является функция у = j(х, С0
).
Решение у=у(х), в каждой точке которого сохраняется единственность решения задачи Коши, называется частным решением
дифференциального уравнения.
Пример.
Найти общее решение дифференциального уравнения 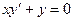 . .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
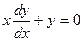
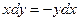
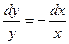
Теперь интегрируем: 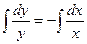
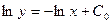
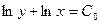
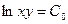

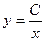 - это общее решение исходного дифференциального уравнения. - это общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0
= 1; y0
= 2, тогда имеем
-4-
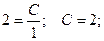
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
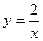
3. Особое решение и его связь с общим решением
Особым решением
дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример: Рассмотрим дифференциальное уравнение:
y = 3(y − sin x) + cos x . (1)
Непосредственной проверкой нетрудно убедиться, что при любом С функция
y = (x + C) + sin x (2)
есть решение этого уравнения. Здесь семейство интегральных кривыхзадается с помощью функции
Ф(x, y,C) = y − (x + C) − sin x .
Для нахождения уравнения огибающей имеем систему
Ф(x, y,C) = y − (x + C) − sin x = 0
Ф (x, y,C) = −3(x + C) = 0
.
Отсюда x + C = 0, и y = sin x. Надо еще проверить, что последнее равенство задает огибающую.
Легко видеь, что при х=х кривые y = sin x и y = (x − x0)3 + sin x имеют общую в точке с абциссой
x = x . Поэтому y = sin x – огибающая семейства кривых (2) и, следовательно,
особое решение уравнения (1).
4. Дифференциальные уравнения первого порядка, разрешенные относительно производных
Дифференциальным уравнением первого порядка
называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
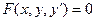
Если такое соотношение преобразовать к виду 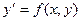 то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной. то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.
Преобразуем такое выражение далее:
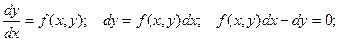
-5-
Функцию f(x,y) представим в виде: 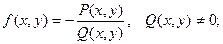 тогда при подстановке в полученное выше уравнение имеем: тогда при подстановке в полученное выше уравнение имеем:
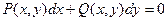
- это так называемая дифференциальная форма
уравнения первого порядка.
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
4.1. Уравнения с разделенными переменными
М(х)dx + N(у)dy=0
М(х)dx + N(у)dy=C – общее решение.
Прим.
4.2. Уравнения с разделяющимися переменными
Определение.
Дифференциальное уравнение 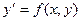 называется уравнением с разделяющимися переменными, если его можно записать в виде называется уравнением с разделяющимися переменными, если его можно записать в виде
 . .
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример.
Решить уравнение 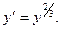


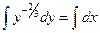
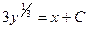
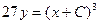 - общий интеграл - общий интеграл
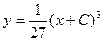 - общее решение - общее решение
4.3.Однородные уравнения.
Определение.
Дифференциальное уравнение вида 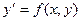 называется однородным
, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов. называется однородным
, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.
Любое уравнение вида 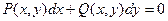 является однородным, если функции P(
x,
y)
и Q(
x,
y)
– однородные функции одинакового измерения. является однородным, если функции P(
x,
y)
и Q(
x,
y)
– однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим однородное уравнение 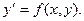
-6-
Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:
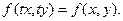
Т.к. параметр t вообще говоря произвольный, предположим, что 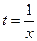 . Получаем: . Получаем:
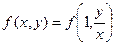
Правая часть полученного равенства зависит фактически только от одного аргумента 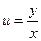 , т.е. , т.е.
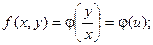
Исходное дифференциальное уравнение таким образом можно записать в виде:
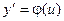
Далее заменяем y = ux
, 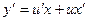 . .

таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
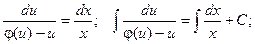
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Пример.
Решить уравнение
-7-
4.4
Уравнения, приводящиеся к однородным.
Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.
Это уравнения вида  . .
Если определитель 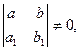 то переменные могут быть разделены подстановкой то переменные могут быть разделены подстановкой

где a и b - решения системы уравнений 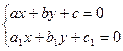
Пример
.
Решить уравнение
-8-
4.5.Линейные уравнения.
Дифференциальное уравнение называется линейным
относительно неизвестной функции и ее производной, если оно может быть записано в виде:
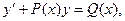
при этом, если правая часть Q(
x)
равна нулю, то такое уравнение называется линейным однородным
дифференциальным уравнением, если правая часть Q(
x)
не равна нулю, то такое уравнение называется линейным неоднородным
дифференциальным уравнением.
P(
x)
и Q(
x)-
функции непрерывные на некотором промежутке a < x < b.
4.6.
Уравнение Бернулли
у+Р(х)у=Q(х)у , m = 0, m = 1.
Решение ищем в виде: у=u v, где u=u(х)
v=v(х)
Пример
.
Решить уравнение
-9-
4.7.
Уравнения в полных дифференциалах
Дифференциальное уравнение первого порядка вида:
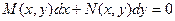 (1) (1)
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции 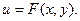
Уравнение (1) называется уравнением в полных дифференциалах, если левая часть уравнения есть полный дифференциал некоторой функции U(х,у), т.е dU=M(x,y)dx+N(x,y)dy, причем с другой стороны dU=
Теорема:
пусть функции M(x,y), N(x,y) и их частные производные
непрерывны для того чтобы уравнение (1) было уравнением в полных дифференциалах необходимо и достаточно выполнения условия:
Пример
.
Решить уравнение
-10-
5. Огибающая семейства интегральных кривых как особое решение
В каждой своей точке огибающая имеет общую касательную с некоторой интегральной кривой семейства Ф(х,у,С) и, следовательно, в каждой точке огибающей направление касательной совпадает с направлением поля в этой точке. Это и означает, что огибающая является интегральной кривой.
Теорема 1
(необходимое условие огибающей). Пусть кривая есть огибающая регулярного семейства Ф(х,у,С). Тогда, если при t=t из [ , ] она касается кривой Ф(х,у,С )=0 (С [С ,С ]) семейства Ф(х,у,С), то число х ,у ,С ,где х =х(t ), у =у(t ), удовлетворяет системе уравнений:
Теорема 2(
достаточный признак огибающей). Пусть семейство Ф(х,у,С) есть регулярное семейство и указана кривая у, заданная уравнениями и функция С=С(t) ( <t< ), причем величины x(t), y(t), C(t) при всех t из [ , ] тождественно
удовлетворяют системе:
Если при этом: 1. кривая у задана в гладкой параметризации;
2. функция С(t) имеет непрерывную производную, неравную тождественно нулю, ни на каком участке из [ , ];
3.
то кривая у есть огибающая семейства Ф(х,у,С).
6. Нахождение кривых, подозрительных на особое решение по
дифференциальному уравнению
Предположим, что правая часть уравнения у = (х,у), определена и непрерывна в некоторой области D и имеет в каждой точке этой области производную по у. Тогда, через каждую точку этой области проходит одна и только одна интегральная кривая уравнения и, следовательно, уравнение у = (х,у) не имеет особых решений. Поэтому, при сделанных предположениях, особое решения уравнения у = (х,у) нужно искать только среди тех кривых, вдоль которых не ограничена.
Будем называть кривые, вдоль которых не ограничена, кривыми, подозрительными на особое решение. Найдя кривую, подозрительными на особое решение, нужно, во-первых, проверить, что она вообще является интегральной кривой, и, во-вторых, убедиться, что в каждой точке ее нарушается единственность решения. Если и то идругое имеет место, то кривая, подозрительными на особое решение, действительно будет особым решением.
-11-
Заключение
-12-
Список литературы:
1. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. 1967г.
2. Матвеев Н.М. Дифференциальные уравнения. 1988г.
3. Матвеев Н.М. Обыкновенные дифференциальные уравнения. 1996г.
-13-
Оглавление
Введение. --------------------------------------------------------------------------------------------------- 2
1. Задача Коши для дифференциального уравнения первого порядка ------------------- 3
1.1. Геометрический смысл ---------------------------------------------------------------------- 3
1.2. Механический смысл ------------------------------------------------------------------------ 3
2. Общее и частное решение дифференциального уравнения первого порядка -------- 4
3. Особое решение и его связь с общим решением ---------------------------------------------- 5
4. Дифференциальные уравнения первого порядка, разрешенные относительно производных ----------------------------------------------------------------------------------------------- 5
5. Огибающая семейства интегральных кривых как особое решение ------------------- 11
6. Нахождение кривых, подозрительных на особое решение по
дифференциальному уравнению -------------------------------------------------------------------- 11
Заключение. ------------------------------------------------------------------------------------------- 12
Список литературы. -------------------------------------------------------------------------------- 13
-1-
ФГОУ ВПО «Чувашский государственный университет имени И.Н. Ульянова».
Кафедра высшей математики.
Курсовая работа:
«Особое решение дифференциальных уравнений
первого порядка».
Выполнил студент
группы ЭЭ-11-09
Зайцев Александр.
Принял преподаватель:
Быкова А.Н.
Чебоксары – 2010г.
|