|
Введение
Высокие темпы информатизации различных видов деятельности в настоящее время привели к тому, что появилась возможность компьютерного моделирования и проектирования сложных систем, изучения их свойств и управления ими в условиях дефицита времени, ограниченности ресурсов, неполноты информации. Однако для исследования характеристик любой системы математическими методами должна быть обязательно выполнена формализация, то есть построена математическая модель. Исследования с помощью математических моделей зачастую являются единственно возможным способом изучения сложных систем и решения важнейших практических задач управления.
Графы оказались хорошей математической моделью широкого класса объектов и процессов. Теория графов применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электроника, машиностроение, архитектура, исследование операций, генетика, психология, социология, экономика, антропология и лингвистика. При этом обычно на графе решаются задачи о достижимости, задачи сетевого планирования, потоковая задача.
Цель исследования, осуществляемого в данной работе, - совершенствование процесса оптимизации сложных задач экономического и сетевого планирования путем разработки технологий и программных средств, использующих графовое моделирование.
Сформулированная цель предопределила следующую совокупность решаемых задач:
1. исследовать эффективность стандартных алгоритмов решения задач оптимизации;
2. разработать и реализовать алгоритмы, позволяющие автоматизировать решение задач оптимизации;
3. реализовать разработанную процедуру в виде программного продукта, соответствующего современным требованиям;
4. провести исследование эффективности разработанной процедуры на представительном множестве тестовых задач;
5. установить параметры, существенно влияющие на эффективность разработанной процедуры, и выработать рекомендации по их настройке;
6. провести апробацию разработанного подхода на реальных практических задачах.
Объект исследования - графовые методы в теории информации.
Предмет исследования - модели структур и сложность решения задач оптимизации.
Использованные методы исследования: теоретический анализ математической литературы, учебников и учебных пособий; изучение и анализ состояния исследуемой проблемы в теоретических основах информатики и дискретной математике; при выполнении работы использовался аппарат системного анализа, теоретических основ информатики, дискретной математики, теории оптимизации, методика создания прикладных интеллектуальных систем.
В основу исследования положена гипотеза: если разработать концептуальные основы графового моделирования структур решений задач оптимизации и реализовать их в виде программных продуктов, то это даст возможность активизировать математическую деятельность изучающих теоретические основы информатики и дискретную математику, повысит качество и результативность решения прикладных задач в экономическом и сетевом планировании.
Научная новизна и теоретическая значимость исследования состоит в том, что в нем:
1. выявлены структурные элементы решения задачи;
2. выявлены отношения, связывающие эти структурные элементы;
3. построены семантические графы первого порядка сложности, моделирующие эти отношения;
4. дана количественная характеристика сложности решения задач;
5. выявлены и систематизированы структуры решений задач оптимизации по числовой характеристике - сложности решения;
6. разработана технология организации работы с программными средствами при решении задач с применением графовых моделей.
1. Элементы теории графов
Наука, занимающаяся графическими представлениями, - геометрия из-за своей наглядности получила широкое распространение уже в древности. Так, задолго до жившего вVI в. до. н. э. Пифагора была известна теорема, которая позже стала носить его имя. Наглядность геометрии широко используют в наше время, в том числе при анализе больших технических и организованных систем, в которых используют графов.
Граф-совокупность вершин и ребер универсальное средство наглядного представления достаточно разнообразных задач (рис.1).
Разнообразные сочетания различных ребер и вершин представляют многообразие возможных графов и их применения. Граф, в котором вершины – прямоугольники и направление ребер не заданы, описывает блок-схему (или структуру) технической системы (рис.2). рисунок 3 - граф-дерево (например описание метода ветвей и границ) - много-уровневая иерархическая система, в которой все вершины распределенные по нескольким уровням. Рисунок 4 – граф с дугами, изображающими связь между вершинами, - сеть.


Сетями представляют различные задачи, в которых исследуют перемещение или выполнение работ во времени. Сеть характеризуется структурой и параметрами дуг. Структура (топология) сети показывает, какие вершины связаны между собой, и направление связывающих их дуг.
Каждую вершину сети нумеруют порядковым номером. Начальную 1 вершину в описании движения потоков называют источником, конечную – стоком. 
Дугу (Рис.5) обозначают двойной индексацией 1-2; 3-4; и т.д. в общем случае дугу обозначают i-j, где i-номер вершины, из которой исходит дуга. Каждая дуга имеет свою характеристику: tij
-продолжительность движения по дуге i-j; cij
– стоимость перемещения; dij
– пропускная способность дуги и т.д.
Зная топологию сети и ее параметры, можно решать самые разнообразные, часто встречающиеся задачи оптимизации.
1.2. Задача коммивояжёра
Задача коммивояжёра (англ.Travelling salesman problem)(коммивояжёр — бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.
Существует несколько частных случаев общей постановки задачи, в частности геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.
Пример
. Пусть имеются 5 пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт (Рис.6).Известно время перевозки из пункта i в пункт j (табл.1). Требуется найти такой маршрут, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в пункте выезда, чтобы его продолжительность была наименьшей.
| Из пункта j
|
В пункт j
|
| 1
|
2
|
3
|
4
|
5
|
| 1
|
0
|
10
|
25
|
25
|
10
|
| 2
|
1
|
0
|
10
|
15
|
2
|
| 3
|
8
|
9
|
0
|
20
|
10
|
| 4
|
14
|
10
|
24
|
0
|
15
|
| 5
|
10
|
8
|
25
|
27
|
0
|
 Решение.
Для решения этой задачи необходимо составить математическую модель. введем обозначения: i и j – номера пунктов выезда и въезда; tij
– время переезда из пункта i в пункт j из таблицы 1 видно, что tij
в общем случае может бы не равно времени переезда в обратном направлении tij
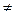 tji
(например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевы переменные: tji
(например, когда один пункт на вершине горы, а другой – у ее подножия). Введем булевы переменные:
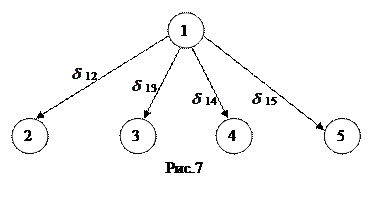 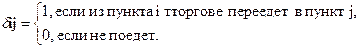
Составим модель (Рис.7). Из пункта 1 можно выехать в любой из пункта 2 или 5, или 3, или 4, или остаться в пункте 1. но при этом можно выехать только в одном единственном направлении. Это условие можно записать так:
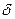 11
+ 11
+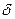 12
+ 12
+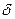 13
+ 13
+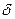 14
+ 14
+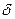 15
=1, или 15
=1, или 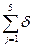 1
j
=1, или для производительного i-го пункта 1
j
=1, или для производительного i-го пункта  ij
=1(i=1,…,5). ij
=1(i=1,…,5).
Эти зависимости обеспечивают выполнение условия, что из каждого пункта выезда производится только один раз и только в одном направлении.
Условие въезда в пункт 1 аналогично условию въезда из пункта 1 (Рис.7). Требование минимальной продолжительности маршрута запишется в виде целевой функции:
min L= t11
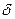 11
+ t12 11
+ t12
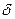 12
+ t13 12
+ t13
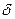 13
+ t14 13
+ t14
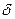 14
+ t15 14
+ t15
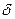 15
+ t21 15
+ t21
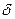 21
+ t22 21
+ t22
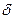 22
+…+ t55 22
+…+ t55
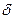 55
, 55
,
где tij
берутся из исходной таблица, а 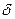 ij
- искомые переменные. ij
- искомые переменные.
Тогда всю задачу можно сформулировать:
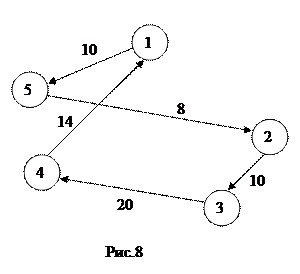
min L = 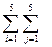 tij tij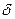 ij, ij,
(*)
В результате решения системы (*) получим (Рис.8) следующие значения 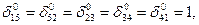 остальные остальные 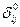 =0; =0;
min L = 10+8+10+20+14=62
переходя от частной к общей постановке, задачу коммивояжера можно сформулировать как:
 min L = min L = 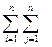 tij tij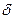 ij, ij,

1.3. Транспортная задача
Транспортная задача – это задача о выборе плана перевозок однородного продукта из пунктов производства в пункты потребления. Пусть имеется m продуктов отправления и n пунктов назначения. Запасы продукта в пунктах отправления обозначим через ai
, потребность в продукте в пункте потребления – bj
.
Расходы на доставку единицы продукта из i-го пункта отправления в j-й пункт назначения равняются Cij
.
Балансовое условие производства и потребления имеет вид
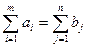
Требуется определить xij
– количество продукта, доставляемого от i-го пункта отправления к j-му пункту потребления. При этом обязательными условиями являются: необходимость удовлетворения всех потребителей, оптимальный план доставки продукта должен обеспечить минимум общей суммы затрат на доставку. Экономико-математическая модель задачи:
min L = 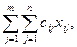

В рассмотренной ЭММ предполагается, что суммарные запасы равны суммарным потребностям. Такая модель называется закрытой. Если это условие не выполняется, то модель называется открытой. Для сведенья открытой модели к закрытой вводится или фиктивный пункт отправления, или фиктивный пункт назначения.
Транспортная задача может быть решена методами линейного программирования. Однако благодаря особенностям переменных задачи разработаны специальные методы ее решения. Наиболее применяемый из них метод потенциалов.
Согласно методу потенциалов, каждому i-му пункту отправления устанавливается потенциал Ui
, который можно интерпретировать как цену продукта в пункте отправления, а каждому j-му пункту назначения устанавливается потенциал Vj
, который можно условно принять как цену продукта в пункте назначения равна его цене в пункте отправления плюс транспортные расходы на его доставку, т.е. Vj
= Ui
+cij
.
Алгоритм решения транспортной задачи методом потенциалов включает следующие этапы:
1. определение начального плана перевозок с помощью метода северо-западного угла, наименьших стоимостей или аппроксимации Фогеля;
2. построение системы потенциалов на основе равенства Vj
= Ui
+cij
;
3. проверка начального плана на оптимальность, и в случае его на оптимальности реализация циклов перераспределения плана перевозок.
Третий этап повторяется до тех пор, пока план перевозок не станет оптимальным.
Пример
. Пусть имеется 3 поставщика и 4 потребителя. Запасы продукта у поставщиков, спрос потребителей и транспортные расходы на доставку единицы продукта от i-го поставщика к j-му потребителю заданы в таблице:
| Поставщик
|
Потребитель
|
Запас
|
| 1
|
2
|
3
|
4
|
| 1
|
3
|
5
|
6
|
2
|
170
|
| 2
|
6
|
4
|
7
|
5
|
250
|
| 3
|
5
|
4
|
6
|
5
|
180
|
| Спрос
|
180
|
230
|
160
|
60
|
600
|
Требуется составить такой план перевозки, чтобы обеспечить минимум общей суммы транспортных расходов.
Решение.
Обозначим xij
– количество продукта, доставляемого от i-го поставщика к j-му потребителю. Тогда модель:
min L = 3x11
+5x12
+6x13
+2x14
+6x21
+4x22
+7x23
+5x24
+5x31
+4x32
+6x33
+5x34

Определим начальный план перевозок с помощью метода северо-западного угла, по которому транспортная матрица заполняется слева на право и сверху вниз. Потребность первого потребителя удовлетворяется за счет первого поставщика. Если потребности оказались выше возможностей первого поставщика, то подключаем второго поставщика. Если запасы первого поставщика больше потребностей первого потребителя, то остаток первого поставщика передаем второму потребителю и т.д. (табл.2).
таблица 2
| Поставщики
|
Потребитель
|
Запас
|
| 1
|
2
|
3
|
4
|
| V1
=3
|
V2
=5
|
V3
=8
|
V4
=7
|
| 1
|
U1
=0
|
3
  150 150
|
5
20
|
6
 6 6
|
2
2
|
170
|
| 2
|
U2
=1
|
 6 6
7
|
 4 4
210
|
4
70
|
5
6
|
250
|
| 3
|
U3
=2
|
5
7
|
 4 4
6
|
6
120
|
5
60
|
180
|
| Спрос
|
150
|
230
|
160
|
60
|
600
|
Мы должны заполнить m+n-1 клеток. Если число заполненных клеток меньше m+n-1 (случай вырождения), то недостающие клетки выбираются произвольно и заполняются нулями. Это так называемые условные поставки.
Первоначальный план содержит шесть перевозок: от первого поставщика – 150 ед. к первому потребителю и 20 ед. ко второму; от второго поставщика – 210 ед. ко второму и 40 ед. к третьему; от третьего поставщика – 120 ед. к третьему потребителю и 60 ед. к четвертому.
Построим систему потенциалов на основе равенства:
Vj
= Ui
+cij
.
Присвоим первому поставщику потенциал U1
=0. От первого поставщика продукт направляют первому и второму потребителям, следовательно, V1
=U1
+c11
=0+3=3; V2
=0+5=5. Зная потенциал второго потребителя, найдем потенциал второго поставщика U2
=V2
.-c22
=5-4=1. потенциал третьего потребителя V3
=1+7=8. потенциал третьего поставщика U3
= 8-6=2. Потенциал четвертого потребителя V4
= 2+5=7. Вычислить потенциалы, помещаем в ( табл.3).
Проверим первоначальный план на оптимальность. План считывается оптимальным, если для всех свободных ячеек выполняется условие:
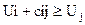
Осуществляем проверку:
U1+с13
=0+6=6<8 – не выполняется, т.е. если бы продукт отправлялся от первого поставщика к третьему потребителю, то его цена у первого поставщика была бы ниже, чем в первоначальном плане.

Рассчитанные значения заносятся в свободные ячейки (табл.3).
таблицы 3
Итерация 1. целевая функция=2590.
| Поставщики
|
Потребитель
|
Запас
|
| 1
|
2
|
3
|
4
|
| V1
=3
|
V2
=0
|
V3
=3
|
V4
=2
|
| 1
|
U1
=0
|
3
  150 150
|
5
5
|
6
6
|
2
 20 20
|
170
|
| 2
|
U2
=-4
|
 6 6
2
|
4
230
|
 4 4
20
|
5
1
|
250
|
| 3
|
U3
=-3
|
5
2
|
4
1
|
6
 140 140
|
5
40
|
180
|
| Спрос
|
150
|
230
|
160
|
60
|
600
|
Для улучшения плана (целевая функция = 2690) необходимо переместить перевозку в ячейку, где условие оптимальности нарушено больше всего, т.е. разность Vj
-(Ui
+cij
) максимальна (ячейка 1.4).
Перемещение производится та, чтобы по отношению к выбранной ячейки образоваться связку. Для этого необходимо провести замкнутую ломанную линию, состоящею из горизонтальных и вертикальных линий, в которой одной из вершин полученного многоугольника является свободная ячейка, а остальные вершины должны находиться в занятых ячейках.
Далее каждое ячейке в связке поочередно присваивается знаки плюс и минус, начиная со свободной. Из ячеек со знаком минус перемещаем перевозки в ячейки со знаком плюс. Чтобы не получить отрицательных перевозок, перемещаем наименьшее количество продукта, которое находится в ячейках связки со знаком минус.
Последовательное улучшение плана в таблицах 3-5.
таблицы 4
Итерация 2. целевая функция=2570.
| Поставщики
|
Потребитель
|
Запас
|
| 1
|
2
|
3
|
4
|
| V1
=3
|
V2
=1
|
V3
=3
|
V4
=2
|
| 1
|
U1
=0
|
3
  130 130
|
5
5
|
6
6
|
2
 40 40
|
170
|
| 2
|
U2
=-3
|
6
20
|
4
230
|
7
4
|
5
2
|
250
|
| 3
|
U3
=-3
|
 5 5
2
|
4
1
|
6
160
|
5
20
|
180
|
| Спрос
|
150
|
230
|
160
|
60
|
600
|
таблицы 5
Итерация 3. целевая функция=2550.
| Поставщики
|
Потребитель
|
Запас
|
| 1
|
2
|
3
|
4
|
| V1
=3
|
V2
=1
|
V3
=4
|
V4
=2
|
| 1
|
U1
=0
|
3
110
|
5
5
|
6
6
|
2
60
|
170
|
| 2
|
U2
=-3
|
6
20
|
4
230
|
7
4
|
5
2
|
250
|
| 3
|
U3
=-2
|
5
2
|
4
2
|
6
160
|
5
3
|
180
|
| Спрос
|
150
|
230
|
160
|
60
|
600
|
|