| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра КТРС
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ ПО ДИСЦИПЛИНЕ
«ОСНОВЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ»
ВАРИАНТ № 10
Выполнил:
Проверил:
Студент Иванов И.И.
Преподаватель Синельников А.В.
Группа: РКС10-32
Новосибирск 2009
Общее задание
Разработать систему кодирования/декодирования циклического кода для  -элементного первичного кода, который обнаруживает  и исправляет  ошибок. Оценить вероятность получения необнаруживаемой ошибки на выходе системы, если  в канале связи меняется от  до  .
Исходные данные
Необходимые для решения задачи исходные данные выбираются по таблице 1 в соответствии с полученным вариантом.
Таблица 1
Исходные данные для вариантов расчетно-графической работы.
| Вариант №
|
Количество элементов в коде
|
Количество исправляемых ошибок
|
Вариант №
|
Количество элементов в коде
|
Количество исправляемых ошибок
|
| 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
5
6
7
8
9
10
5
6
7
8
9
10
5
6
7
8
9
10
5
6
|
1
5
3
2
4
1
2
4
6
1
3
2
3
3
5
4
2
3
4
2
|
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
7
8
9
5
6
7
8
6
7
5
5
6
7
6
9
8
10
5
5
8
|
4
3
1
5
1
2
5
6
1
3
5
2
4
6
3
4
2
4
5
3
|
Этапы выполнения работы
1. Определение числа проверочных элементов избыточного кода.
2. Выбор образующего многочлена для построения кода, указанного в задании.
3. Расчёт матрицы синдромов для однократной ошибки.
4. Построение функциональной схемы устройств кодирования-декодирования полученного кода.
5. Построение графика появления необнаруживаемой ошибки при заданном изменении вероятности ошибки в канале связи.
ЗАДАНИЕ ВАРИАНТА
Разработать систему кодирования/декодирования для k = 8-элементного первичного кода, когда код обнаруживает и исправляет tИ
= 1-ошибку. Оценить вероятность обнаружения ошибки на выходе системы передачи, если вероятность ошибки в канале связи РОШ
меняется от  до  .
РЕШЕНИЕ
Определение количества поверочных элементов
r
.
Исходя из того, что k = 8 и tИ
= 1, решаем систему уравнений:
Откуда следует:
Составляем таблицу:
| 
|
|
| 1
2
3
4
|
1
2
5
12
|
Откуда определяем: r = 4, n = k + r = 8 + 4 = 12.
Выбор образующего полинома
После определения проверочных разрядов r, выбираем образующий полином G(x) (многочлен) степени, равной r.
Образующий полином G(x) должен обладать некоторыми свойствами:
1) Остатки от деления должны быть все разные, т.е. его нельзя составить из степеней низших порядков, он неприводимый.
2) Число остатков у этого полинома должно быть равно количеству ошибок в коде, т.е. такие полиномы примитивные.
С помощью таблицы образующих полиномов можно найти необходимый полином. В приводимой таблице указаны некоторые свойства этих многочленов и соотношения между ними. Приводятся примитивные многочлены с минимальным числом ненулевых коэффициентов. Многочлены даны в восьмеричном представлении.
Двойственный многочлен неприводимого многочлена также неприводим, а двойственный многочлен примитивного многочлена примитивен. Поэтому каждый раз в таблице приводится либо сам многочлен, либо двойственный многочлен. Каждая запись в таблице, оканчивающаяся некоторой буквой, соответствует некоторому неразложимому многочлену указанной степени. Для степеней от 2 до 16 этими многочленами, а также двойственными к ним исчерпываются все неразложимые многочлены этих степеней.
Буквы, которые приведены после восьмеричного представления многочлена, дают о нем следующую информацию:
A
,
B
, С,
D
Не примитивный
Е,
F
,
G
, Н
Примитивный
A
,
B
, Е,
F
Корни линейно зависимы
С,
D
,
G
, Н
Корни линейно независимы
A
,
C
, Е,
G
Корни двойственного многочлена линейно зависимы
B
,
D
,
F
, Н
Корни двойственного многочлена линейно независимы
Выписываем часть таблицы неприводимых полиномов:
Из таблицы выбираем полином (1 23F) и затем переводим из восьмеричного в двоичное представление:
Получили образующий полином:
G(x) = x4
+ x + 1.
Проверка образующего полинома
1. Определяем необходимое кодовое расстояние:
2. Вычисляем: f(x) = xk
-1
= x7
= 10000000
3. Находим: f(x)xr
= x11
= 100000000000
4. Поделим f(x)xr
на G(x):
x11
x4
+ x + 1
x11
+ x8
+ x7
x7
+ x4
+ x3
+ x
x8
+ x7
x8
+ x5
+ x4
x7
+ x5
+ x4
x7
+ x4
+ x3
x5
+ x3
x5
+ x2
+ x
x3
+ x2
+ x = r(x) = 1110
Полученный остаток от деления является комбинацией проверочных элементов:
r(x) = 1110
5. Записываем многочлен комбинации:
F(x) = f(z)xr
+ r(x) = 100000001110
Определяем вес многочлена (количество единиц в комбинации): V = 4.
6. Сравниваем V с d0
, поскольку выполняется условие: V ³ d0
, то выбранный полином подходит как образующий.
Построение матрицы синдромов для однократной ошибки
Для определения элементов матрицы синдромов будем вносить ошибку в кодовую комбинацию (F(x) = 100000001110) поочерёдно начиная со старшего разряда, затем делить на образующий полином, полученный остаток и будет одной из строк матрицы синдромов. Пусть ошибка произошла в самом старшем разряде, тогда она имеет вид 000000001110, т.е. деление такого числа на образующий полином и есть это число. Следовательно это синдром для ошибки в разряде а1. Определим синдромы для остальных разрядов.
для а2:
x10
x4
+ x + 1
x10
+ x7
+ x6
x6
+ x3
+ x2
+ 1
x7
+ x6
x7
+ x4
+ x3
x6
+ x4
+ x3
x6
+ x3
+ x2
x4
+ x2
x4
+ x + 1
x2
+ x + 1 = s(x) = 0111
для а3:
x9
x4
+ x + 1
x9
+ x6
+ x5
x5
+ x2
+ x
x6
+ x5
x6
+ x3
+ x2
x5
+ x3
+ x2
x5
+ x2
+ x
x3
+ x = s(x) = 1010
для а4:
x8
x4
+ x + 1
x8
+ x5
+ x4
x4
+ x + 1
x5
+ x4
x5
+ x2
+ x
x4
+ x2
+ x
x4
+ x + 1
x2
+ 1 = s(x) = 0101
для а5:
x7
x4
+ x + 1
x7
+ x4
+ x3
x3
+ 1
x4
+ x3
x4
+ x + 1
x3
+ x + 1 = s(x) = 1011
для а6:
x6
x4
+ x + 1
x6
+ x3
+ x2
x2
x3
+ x2
= s(x) = 1100
для а7:
x5
x4
+ x + 1
x5
+ x2
+ x x
x2
+ x = s(x) = 0110
для а8:
x4
x4
+ x + 1
x4
+ x + 1 1
x + 1 = s(x) = 0011
Таким образом, матрица синдромов имеет вид:
Полученная матрица синдромов используется для алгоритма построения дешифратора ошибок разрабатываемого далее декодера.
Схема кодера циклического кода (12, 8)
Образующий полином G(x) можно представить в виде:
G(x) = g4
x4
+ g3
x3
+ g2
x2
+ g1
x + g0
, где g4
= 1, g3
= 0, g2
= 0, g1
= 1, g0
= 1.
Тогда устройство кодирования имеет вид:
Рис.1. Схема устройства кодирования циклического кода (12, 8).
Принцип работы устройства:
В исходном состоянии ключ находится в положении 1, на вход устройства поступает первичная кодовая комбинация f(x) (начиная со старшего разряда). Через k-тактов вся первичная кодовая комбинация поступит на выход, а в результате деления (благодаря обратной связи) образуется остаток. Ключ переключается в положение 2. Таким образом, через n-тактов на выходе получим F(x).
Схема декодера циклического кода (12, 8).
Рис.2. Схема устройства декодирования циклического кода (12, 8).
Принцип работы устройства:
Исходная комбинация F(x) подается в буферный регистр и одновременно в декодирующий регистр. Если с приходом последнего символа, зафиксирован нулевой остаток (синдром 0000), то ошибок нет, если же не нулевой, то есть. Принятая комбинация подается через выходной сумматор, и искаженный сигнал исправляется.
Оценка вероятности обнаруживаемой ошибки на выходе системы передачи
Определим вероятность ошибочного приема кодовой комбинации в условиях биномиального распределения ошибок. При помехоустойчивом кодировании различают ошибки двух типов:
· Обнаруживаемые или исправляемые кодом.
· Необнаруживаемые ошибки.
Вероятности появления необнаруживаемых ошибок (в режиме исправления):
С помощью программы в среде МАТКАД производим расчеты и получаем графическую зависимость вероятности необнаруживаемых ошибок от вероятности ошибки элемента:
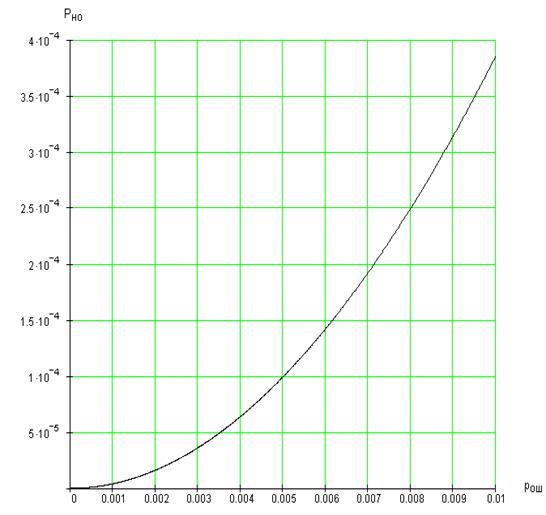
Рис.3. График зависимости вероятности не обнаруживаемой ошибки Рно
на выходе системы передачи от вероятности ошибки в канале связи Рош
.
Из графика видим, что с увеличением вероятности ошибки в канале вероятность обнаружения ошибки на выходе системы передачи также увеличивается.
ЛИТЕРАТУРА
1. Питерсон У., Уэлдон Э. Коды исправляющие ошибки. – М.: Мир, 1976г.
2. Мак-Вильямс Ф.Дж., Слоэн Н.Дж. Теория кодов, исправляющих ошибки. – М.: Радио и связь, 1979г.
3. Основы передачи дискретных сообщений: Учебник для вузов / Ю.П. Куликов, В.М. Пушкин, Г.И. Скворцов и др.: Под ред. В.М. Пушкина. – М.: Радио и связь, 1992.- 288 с., ил.
|
