|
I. Общая теория статистики.
Вариант №5
Задание1. Группировка статистических данных.
1.1 По одному группировочному признаку для заданного экономического показателя произвести простую группировку закрытым интервалом.
Величину интервала рассчитать по формуле:
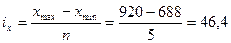
Число групп определяется по формуле:
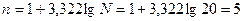
Таблца1
Группировка предприятий по показателю...закрытым интервалом
| Груп па
|
Интервал группы
|
Количество предприятий
|
Номер предприятия
|
| Ι
|
688-734,4
|
2
|
3,5
|
| ΙΙ
|
734,4-780,8
|
3
|
1,3,11
|
| ΙΙΙ
|
780,8-827,2
|
4
|
1,7,17,18
|
| ΙV
|
827,2-873,6
|
1
|
12
|
| V
|
873,6-920
|
2
|
6, 13
|
1.2 Произвести аналитическую группировку по двум признакам.
Таблица 2
Сложная аналитическая группировка предприятий по двум признакам
| № группы
|
Интервал группы по первому показателю Х
|
Количество предприятий
|
Средний интервал первого показателя Хi´
|
Второй показатель и его величина
У
|
Среднее значение второго показателя
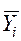
|
Изменение среднего значения второго показателя
 - - 
|
| Ι
|
688-734,4
|
2
|
711,2
|
5;9
|
7
|
-
|
| ΙΙ
|
734,4-780,8
|
3
|
757,6
|
6;10
|
8
|
1
|
| ΙΙΙ
|
780,8-827,2
|
4
|
804
|
6; 10;15;13
|
11
|
3
|
| ΙV
|
827,2-873,6
|
1
|
850,4
|
9
|
9
|
-2
|
| V
|
873,6-920
|
2
|
896,8
|
12;12
|
12
|
3
|
1.3 Рассчитать силу связи между признаками для всей совокупности попарно и сделать выводы о характере связей (прямая, обратная).
Сила связи для всей совокупности рассчитывается по формуле:
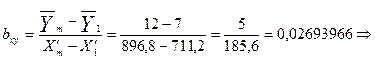 связь прямая связь прямая
Силу связи попарно рассчитывается по формуле:
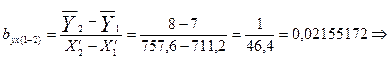 связь прямая связь прямая
Задание 2. Статистические таблицы и графики
2.1 Построить столбиковую диаграмму для первого показателя для десяти предприятий.
Данные первого показателя Столбиковая диаграмма по первому показателю
| №предприятия
|
Показатель
|
| 1
|
780
|
| 2
|
940
|
| 3
|
720
|
| 4
|
670
|
| 5
|
688
|
| 6
|
920
|
| 7
|
795
|
| 8
|
460
|
| 9
|
330
|
| 10
|
940
|

2.2 Построить секторную диаграмму для второго показателя для десяти предприятий.
Данные второго показателя Секторная диаграмма по второму показателю
| №предприятия
|
Показатель
|
Размер сектора в %соотношении
|
| 1
|
6
|
6.8%
|
| 2
|
7
|
8%
|
| 3
|
5
|
5.7%
|
| 4
|
10
|
11.4%
|
| 5
|
9
|
10.2%
|
| 6
|
12
|
13.6%
|
| 7
|
10
|
11.4%
|
| 8
|
8
|
9%
|
| 9
|
7
|
8%
|
| 10
|
14
|
15.9%
|
| |
Итого:88
|
Итого:100%
|

3.2 По двум показателям рассчитать относительные величины интенсивности. Результаты представить в таблице 4.
Таблица 4
Относительная величина интенсивности
| Предприятие
|
Первый показатель
|
Второй показатель
|
Относительная величина интенсивности
|
| 1
|
780
|
74
|
6
|
| 2
|
940
|
88
|
7
|
| 3
|
720
|
68
|
5
|
| 4
|
670
|
60
|
10
|
| 5
|
688
|
65
|
9
|
| 6
|
920
|
82
|
12
|
| 7
|
795
|
73
|
10
|
| 8
|
460
|
51
|
8
|
| 9
|
330
|
46
|
7
|
| 10
|
940
|
85
|
14
|
| 11
|
760
|
72
|
10
|
| 12
|
840
|
78
|
9
|
| 13
|
910
|
82
|
12
|
| 14
|
580
|
50
|
11
|
| 15
|
960
|
89
|
10
|
| 16
|
680
|
61
|
9
|
| 17
|
810
|
76
|
15
|
| 18
|
800
|
72
|
13
|
| 19
|
390
|
40
|
7
|
| 20
|
550
|
52
|
9
|
Задание 4. Средние величины.

4.1 Рассчитать простую среднюю арифметическую величину по одному показателю:

4.2 Рассчитать среднюю арифметическую взвешенную величину интервального ряда для показателя ,по которому проводилась группировка по формуле:

Таблица 5
Расчёт средней величины интервального ряда
| № группы
|
Интервал группы
|
Количество предприятий fi
|
Середина интервала Х´i
|
Произведение
Х´I fi
|
| Ι
|
688-734,4
|
2
|
711,2
|
1422,4
|
| ΙΙ
|
734,4-780,8
|
3
|
757,6
|
2272,8
|
| ΙΙΙ
|
780,8-827,2
|
4
|
804
|
3216
|
| ΙV
|
827,2-873,6
|
1
|
850,4
|
850,4
|
| V
|
873,6-920
|
2
|
896,8
|
1793,6
|
4.3 Рассчитать моду для одного показателя, по которому проводилась группировка.
Формула для расчета:
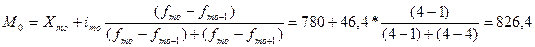
Таблица 6
Расчёт моды показателя
| № группы
|
Интервал группы
|
Количество предприятий fi
|
| Ι
|
688-734,4
|
2
|
| ΙΙ
|
734,4-780,8
|
3
|
| ΙΙΙ
|
780,8-827,2
|
4
|
| ΙV
|
827,2-873,6
|
1
|
| V
|
873,6-920
|
2
|
-Модальный интервал
4.4 Определить медиану для одного показателя, для чего упорядочить ряды, т.е. расположить их в порядке возрастания и убывания.
Таблица 7
Расчёт медианы
| № предприятия
|
Величина показателя
|
| 1
|
330
|
| 2
|
390
|
| 3
|
460
|
| 4
|
550
|
| 5
|
580
|
| 6
|
670
|
| 7
|
680
|
| 8
|
688
|
| 9
|
720
|
| 10
|
760
|
| 11
|
780
|
| 12
|
795
|
| 13
|
800
|
| 14
|
810
|
| 15
|
840
|
| 16
|
910
|
| 17
|
920
|
| 18
|
940
|
| 19
|
940
|
| 20
|
960
|
Мe=770т.
4.5 Определить медиану для интервального ряда по одному показателю, по которому проводилась группировка, по формуле:

Таблица 8
Расчет медианы вариационного интервального ряда
| № группы
|
Интервал группы х
|
Число предприятий f
|
Сумма накопленных частот ∑f
|
| Ι
|
330-456
|
2
|
2
|
| ΙΙ
|
456-582
|
3
|
5
|
| ΙΙΙ
|
582-708
|
3
|
8
|
| ΙV
|
708-834
|
6
|
14
|
| V
|
834-960
|
6
|
20
|
Задание 5. Статистическое изучение вариаций
5.1 Рассчитать показатели вариаций для вариационного ряда.
Таблица 9
| № группы
|
Интервал группы
(показатель х)
|
Число предприятий
f
|
Расчётные показатели
|
| 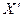
|

|
(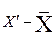 ) )
|

|
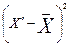
|
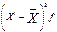
|
| Ι
|
688-734,4
|
2
|
711,2
|
1422,4
|
-321
|
642
|
103041
|
206082
|
| ΙΙ
|
734,4-780,8
|
3
|
757,6
|
2272,8
|
-195
|
582
|
38025
|
114075
|
| ΙΙΙ
|
780,8-827,2
|
4
|
804
|
3216
|
-69
|
207
|
4761
|
14283
|
| ΙV
|
827,2-873,6
|
1
|
850,4
|
850,4
|
57
|
342
|
3249
|
19494
|
| V
|
873,6-920
|
2
|
896,8
|
1793,6
|
183
|
1098
|
33489
|
200934
|
Формулы для расчёта
:
1. 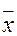 -средняя арифметическая взвешенная: -средняя арифметическая взвешенная:
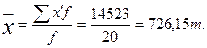
2.
R-размах вариации:
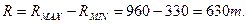
3.Среднее линейное отклонение:
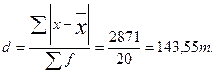
4.Дисперсия 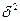 : :
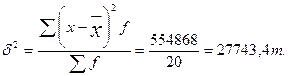
5.Среднее квадратичное отклонение:
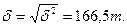
6.Коэфициент вариации:
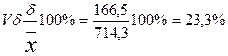
7.Коэффициент осцилляции:
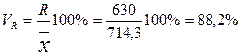
|