СОДЕРЖАНИЕ
| Задача 1 |
3 |
| Задача 2 |
6 |
| Задача 3 |
7 |
| Задача 4 |
9 |
| Задача 5 |
10 |
| Задача 6 |
14 |
| Задача 7 |
16 |
| Список использованных источников |
18 |
Задача 1.
За отчетный период работа предприятий торговли района характеризуется данными (таблица 1).
Таблица 1
| Предприятия |
Розничный товарооборот, тыс. руб. |
Издержки обращения, тыс. руб. |
| 1
|
2
|
3
|
| 1 |
511 |
30,0 |
| 2 |
560 |
34,0 |
| 3 |
800 |
46,0 |
| 4 |
465 |
30,9 |
| 5 |
228 |
15,9 |
| 6 |
392 |
25,2 |
| 7 |
640 |
42,0 |
| 8 |
404 |
27,0 |
| 9 |
200 |
16,4 |
| 10 |
425 |
34,8 |
| 11 |
570 |
37,0 |
| 12 |
472 |
28,6 |
| 13 |
250 |
18,7 |
| 14 |
665 |
39,0 |
| 15 |
650 |
36,0 |
| 16 |
620 |
36,0 |
| 17 |
383 |
25,0 |
| 18 |
550 |
38,5 |
| 19 |
750 |
44,0 |
| 20 |
660 |
37,0 |
| 21 |
452 |
27,0 |
| 22 |
563 |
35,0 |
1. Для изучения зависимости между объемом розничного товарооборота и издержками обращения проведите группировку предприятий торговли по объему товарооборота, образовав 5 групп с равными интервалами. Каждую группу предприятий и совокупность в целом охарактеризуйте – числом предприятий, объемом товарооборота, издержками обращения.
По каждой группе рассчитайте вышеперечисленные показатели в среднем на 1 предприятие, а также относительный уровень издержек обращения (издержки обращения / розничный товарооборот*100%). Сделайте выводы.
2.Постройте гистограмму ряда распределения по объему товарооборота. Сделайте выводы.
Решение:
1. Ширина равного интервала определяется по формуле (1):

Сформируем интервалы группировки – (200 – 320); (320 – 440); (440 – 560); (560 – 680); (680 – 800). Для построения самой группировки построим рабочую таблицу 2.
Таблица 2
| № группы с интервалом группировки |
Предприятия |
Розничный товарооборот, тыс. руб. |
Издержки обращения, тыс. руб. |
| 1 (200 – 320) |
5 |
228 |
15,9 |
| 9 |
200 |
16,4 |
| 13 |
250 |
18,7 |
| Итого
|
3
|
678
|
51
|
| 2 (320 – 440) |
6 |
392 |
25,2 |
| 8 |
404 |
27,0 |
| 10 |
425 |
34,8 |
| 17 |
383 |
25,0 |
| Итого
|
4
|
1604
|
112
|
| 3 (440 – 560) |
1 |
511 |
30,0 |
| 4 |
465 |
30,9 |
| 12 |
472 |
28,6 |
| 18 |
550 |
38,5 |
| 21 |
452 |
27 |
| Итого
|
5
|
2450
|
155
|
| 4 (560 – 680) |
2 |
560 |
34 |
| 7 |
640 |
42 |
| 11 |
570 |
37 |
| 14 |
665 |
39 |
| 15 |
650 |
36 |
| 16 |
620 |
36 |
| 20 |
660 |
37 |
| 22 |
563 |
35 |
| Итого
|
8
|
4928
|
296
|
| 5 (680 – 800) |
3 |
800 |
46 |
| 19 |
750 |
44 |
| Итого
|
2
|
1550
|
90
|
По итоговым данным из рабочей таблицы построим аналитическую группировку, рассчитав все показатели в среднем по группам, а также другие необходимые показатели. Результаты представлены в таблице 3.
Таблица 3
| № группы |
Число предприятий |
Розничный товарооборот, тыс. руб. |
Издержки обращения, тыс. руб. |
Относительный уровень издержек обращения, % |
| итого |
в среднем |
итого |
в среднем |
| 1 |
3 |
678 |
226 |
51 |
17 |
7,52 |
| 2 |
4 |
1604 |
410 |
112 |
28 |
6,83 |
| 3 |
5 |
2450 |
490 |
155 |
31 |
6,33 |
| 4 |
8 |
4928 |
616 |
296 |
37 |
6 |
| 5 |
2 |
1550 |
775 |
90 |
45 |
5,81 |
2. Вывод: Как видно из таблицы 3, с увеличением розничного товарооборота происходит в среднем по группам увеличение издержек обращения, следовательно, между этими показателями есть прямая связь. Но при увеличении этих показателей – относительный уровень издержек обращения уменьшается в среднем по группам, следовательно, здесь возникает обратная связь.
Гистограмма ряда распределения по объему товарооборота представлена на рисунке 1.
| Количество предприятий |
| 8 |
| 5 |
| 4 |
| 3 |
| 2 |
| 200-320 |
320-440 |
440-560 |
560-680 |
680-800 |
| Объем розничного товарооборота |
Рисунок 1 – Распределение объема товарооборота
Задача 2
.
Имеются данные о работе малых предприятий за текущий период (таблица 4).
Таблица 4
| Предприятия |
Фактический объем реализации, руб. |
Средний объем реализации на 1 работника, руб. |
Прибыль в % к объему реализации |
| 1 |
19000 |
3800 |
19 |
| 2 |
16000 |
4000 |
20 |
| 3 |
20000 |
5000 |
26 |
Рассчитайте по малым предприятиям в целом:
1. Средний объем реализации на 1 работника.
2. Среднюю рентабельность реализованной продукции (прибыль/объем реализованной продукции*100%).
Укажите, какой вид средней необходимо применять для вычисления и почему.
Решение:
| Предприя-тия |
Фактичес-кий объем реализации, руб. (
fi
,
Wi
)
|
Средний объем реализации на 1 работника, руб. (
yi
)
|
Прибыль в % к объему реализации (
xi
)
|
Количество работников, чел. (
Wi
/
yi
)
|
Прибыль, руб. (
xi
∙
fi
)
|
| 1 |
19000 |
3800 |
19 |
5 |
3610 |
| 2 |
16000 |
4000 |
20 |
4 |
3200 |
| 3 |
20000 |
5000 |
26 |
4 |
5200 |
| Итого
|
55000
|
13
|
12010
|
1. Составим логическую формулу среднего объема реализации на 1 работника:
Средний объем реализации на 1 работника = фактический объем реализации / количество работников.
Так как нам неизвестен числитель логической формулы, то мы применяем среднюю гармоническую взвешенную
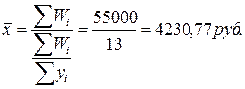
2. Рассчитаем среднюю рентабельность реализованной продукции = (прибыль / объем реализованной продукции)*100%.
Так как нам известен знаменатель этой логической формулы, но неизвестен числитель, то мы применяем среднюю арифметическую

Задача 3.
Имеются следующие данные 5% выборочного механического обследования студентов одного из вузов о затратах времени на дорогу до института (таблица 5).
Таблица 5
| Затраты на дорогу до института, час. |
До 0,5
|
0,5 – 1,0
|
1,0 – 1,5
|
1,5 – 2,0
|
Более 2,0
|
| Число студентов в % к итогу, (
fi
)
|
7
|
18
|
32
|
36
|
7
|
По этим данным определите:
1. Средние затраты времени на дорогу, дисперсию и среднеквадратическое отклонение затрат времени, коэффициент вариации. Сделайте выводы.
2. С вероятностью 0.997 определите для всех студентов вуза возможные пределы средних затрат времени на дорогу, а также возможные пределы доли студентов, затрачивающих на дорогу менее 1 часа.
Решение:
1. Для расчета построим расчетную рабочую таблицу 6.
Таблица 6
| Затраты на дорогу до института, час. |
Число студентов в % к итогу (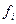 ) ) |
Середина,xi
|
 |
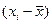
|
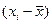 2
2
|
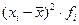
|
| До 0,5 |
7 |
0,25 |
1,75 |
-1,09 |
1,19 |
8,33 |
| 0,5 – 1,0 |
18 |
0,75 |
13,5 |
-0,59 |
0,35 |
6,3 |
| 1,0 – 1,5 |
32 |
1,25 |
40 |
-0,09 |
0,01 |
0,32 |
| 1,5 – 2,0 |
36 |
1,75 |
63 |
0,41 |
0,17 |
6,12 |
| Более 2,0 |
7 |
2,25 |
15,75 |
0,91 |
0,83 |
5,81 |
| Итого
|
100
|
-
|
134
|
-
|
-
|
26,88
|
Находим середину по формуле 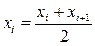 , результаты вносим в таблицу 6. , результаты вносим в таблицу 6.
Средние затраты времени на дорогу равны:
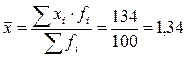 часа часа
 Дисперсия равна: Дисперсия равна:
Среднеквадратическое отклонение равно:
s
=
Ö
s
2
=
Ö0,27 = 0,52
Коэффициент вариации равен:Вывод: Средние затраты времени на дорогу составили 1,34 часа, средний разброс индивидуальных значений затрат времени вокруг средней составили 0,52 часа. Так как коэффициент вариации равен 38,8 %, т.е. > 33 %, то распределение расходов на рекламу является совокупностью неоднородной и колебания неустойчивые.
2. Определяем ошибки выборки. Так как вероятность Р=0,997, то коэффициент доверияt=3. Рассчитаем выборочную долю для признака – затраты на дорогу менее 1,1 часа. Так как данные затраты на дорогу имеют 1 и 2 группы студентов в выборке, то 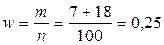 . .
Дисперсия выборочной доли:
s2
w
= w∙(1 – w) = 0,25∙(1-0,25)=0,188.
Определим предельную ошибку выборки для среднего по формуле:

Определим предельную ошибку выборки для доли по формуле:
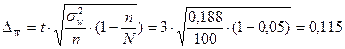
Построим доверительный интервал для среднего по формуле:
Построим доверительный интервал для генеральной выборочной доли по формуле:
Вывод: С вероятностью 0,997 можно утверждать, что средние затраты на дорогу до института находится в пределах от 1,19 до 1,49 часа, а доля всех затрат на дорогу, имеющих менее 1,1 часа, находится в пределах от 0,135 часа до 0,365 часа.
ЗАДАЧА 4.
Товарные запасы в торговой сети региона составили, млн. руб. – таблица 7.
Таблица 7
| 1 января |
1 февраля |
1 марта |
1 апреля |
1 мая |
1 июня |
1 июля |
| 22,4 |
23,5 |
20,8 |
22,2 |
24,6 |
25,0 |
26,2 |
Исчислите средние товарные запасы за 1 и 2 квартал и за полугодие, а также процент изменения средних запасов за 2 квартал по сравнению с 1 кварталом.
Решение:
Расчет средних товарных запасов по формулесредней хронологической простой при равноотстоящих уровнях ряда:Определяем средний товарный запас за 1 квартал:
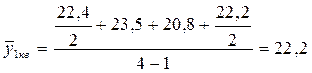 млн. руб. млн. руб.
Определяем средний товарный запас за 2 квартал:
 млн. руб. млн. руб.
Определяем средний запас за полугодие:
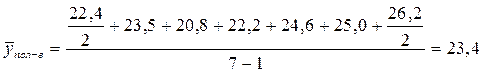 млн. руб. млн. руб.
Определяем процент изменения средних запасов за 2 квартал по сравнению с 1 кварталом:
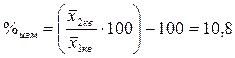 % %
ЗАДАЧА 5.
Динамика выпуска проката по г. Новокузнецку характеризуется следующими данными – таблица 8.
Таблица 8
| Вид продукции |
Год |
| 1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
| Прокат готовый, млн. т. |
6,2
|
5,3
|
5,1
|
4,2
|
6,1
|
7,2
|
7,3
|
На основе этих данных найдите:
1. Абсолютный прирост, темпы роста и прироста (цепные и базисные), а также абсолютное значение одного процента прироста. Результаты изложите в табличной форме.
2. Среднегодовой уровень ряда и среднегодовой темп роста и прироста. Динамику выпуска продукции изобразите на графике. Сделайте выводы.
3. Найдите уравнение основной тенденции (тренда) методом аналитического выравнивания. Тренд изобразите на том же графике.
Решение:
1. Для расчета построим рабочую таблицу 9.
Таблица 9
| Год |
Прокат готовый, млн.т. |
Абсолютный прирост, % |
Темп роста, % |
Темп прироста, % |
Абсолютное значение одного процента прироста |
| базисный |
цепной |
базисный |
цепной |
базисный |
цепной |
| 1995 |
6,2 |
- |
- |
- |
- |
- |
- |
- |
| 1996 |
5,3 |
-0,9 |
-0,9 |
85,48 |
85,48 |
-14,52 |
-14,52 |
0,062 |
| 1997 |
5,1 |
-1,1 |
-0,2 |
82,26 |
96,23 |
-17,74 |
-3,77 |
0,053 |
| 1998 |
4,2 |
-2 |
-0,9 |
67,74 |
82,35 |
-32,26 |
-17,65 |
0,051 |
| 1999 |
6,1 |
-0,1 |
1,9 |
98,39 |
145,24 |
-1,61 |
45,24 |
0,042 |
| 2000 |
7,2 |
1 |
1,1 |
116,13 |
118,03 |
16,13 |
18,03 |
0,061 |
| 2001 |
7,3 |
1,1 |
0,1 |
117,74 |
101,39 |
17,74 |
1,39 |
0,072 |
| Итого |
41,4 |
0,341 |
Все эти показатели определяются по формулам:
| Абсолютный прирост: |
| базисный – D
yб
= yi
– y0
;
|
| цепной – D
yц
= yi
– yi–-1
.
|
| Темп прироста: |
| базисный – Tпpб
= Tpб
– 100;
|
| цепной – Tпpц
= Tpц
– 100.
|
| Абсолютное значение 1% прироста: |
| А%
=
D
yц
/ Tпpц
= 0,01
∙
yi–-1.
|
| Темп роста: |
| базисный – Tpб
= yi
/ y0
∙
100;
|
| цепной – Tpц
= yi
/ yi–-1
∙
100.
|
Вывод: за весь период (1995-2001 гг.) выпуск проката увеличился на 1,1 млн. т. или на 17,74 %. При этом выпуск проката возрастал в 1999-2001 гг. на 3,1 млн. т. или на 64,66 % и снижался 1996-1998 гг. на 2 млн. т. или на 64,52 %.

Рисунок 2 – Динамика выпуска проката
2.Средний уровень ряда:
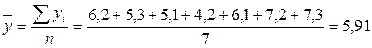 млн. т. млн. т.
Среднегодовые темпы роста и прироста:
 
Средний абсолютный прирост:
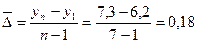
Среднее абсолютное значение 1% прироста:
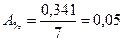 млн. т. млн. т.
Вывод: В среднем в год за весь период выпуск проката составил 5,91 млн. т., он увеличивался в среднем на 0,18 млн. т. или 2,06%, при этом на 1% в среднем приходилось 0,05 млн. т.
3. Для определения параметров модели построим расчетную таблицу 10.
Таблица 10
| Год |
Прокат готовый, млн.т. y
i y
i
|
t
|
t2
|
 y
i
∙
t y
i
∙
t
|
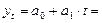  |
| 1995 |
6,2 |
-3 |
9 |
-18,6 |
5,03 |
| 1996 |
5,3 |
-2 |
4 |
-10,6 |
5,32 |
| 1997 |
5,1 |
-1 |
1 |
-5,1 |
5,61 |
| 1998 |
4,2 |
0 |
0 |
0 |
5,9 |
| 1999 |
6,1 |
1 |
1 |
6,1 |
6,19 |
| 2000 |
7,2 |
2 |
4 |
14,4 |
6,48 |
| 2001 |
7,3 |
3 |
9 |
21,9 |
6,77 |
| Итого |
41,4 |
0 |
28 |
8,1 |
41,3 |
Для определения типа модели тренда используем уравнение прямой:
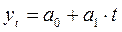 , ,
| где: t – время; |
| yt
– значение уровня ряда, полученное по модели; |
| a0
, a1
, – параметры модели, определяемые из системы нормальных уравнений. |
По данным таблицы 10 определим параметры линейной модели
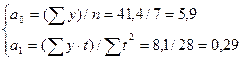
Таким образом, получаем следующий вид модели тренда  . По ней рассчитываем значение yt
. Строим график тренда рисунок 2а. . По ней рассчитываем значение yt
. Строим график тренда рисунок 2а.

Рисунок 2а – Динамика выпуска проката и модель тренда
Задача 6.
Имеются данные о реализации товара "С", тыс. т. таблица 11.
Таблица 11
| Месяц |
Год |
| 1994 |
1995 |
1996 |
| Январь |
50,2 |
56,8 |
65,5 |
| Февраль |
47,2 |
50,9 |
58,7 |
| Март |
55,9 |
61,0 |
64,5 |
| Апрель |
58,1 |
66,8 |
74,0 |
| Май |
57,4 |
62,7 |
76,3 |
| Июнь |
59,2 |
70,0 |
70,3 |
| Июль |
43,0 |
54,2 |
55,7 |
| Август |
37,8 |
46,6 |
50,8 |
| Сентябрь |
46,0 |
50,4 |
57,3 |
| Октябрь |
51,4 |
54,9 |
58,5 |
| Ноябрь |
55,1 |
60,5 |
62,3 |
| Декабрь |
51,6 |
62,0 |
62,8 |
По имеющимся данным определите сезонность реализации товара "С" методом простой средней. Постройте график сезонной волны и сделайте выводы.
Решение:
Поскольку объем реализации товара "С" от года к году существенно не меняется, индекс сезонности определяется по формуле:
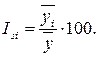
Расчет индексов осуществляется так:
1. Определяются по методу простой средней – средние уровни для каждого месяца:
для января – 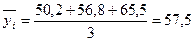 тыс.т. и т.д. Данные вносятся в таблицу 12. тыс.т. и т.д. Данные вносятся в таблицу 12.
Таблица 12.
| Месяц |
Год |
1994-1996 гг., тыс.т. (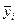 ) ) |
Индексы сезонности, % ( ) ) |
| 1994 |
1995 |
1996 |
| Январь |
50,2 |
56,8 |
65,5 |
57,50 |
100,2 |
| Февраль |
47,2 |
50,9 |
58,7 |
52,27 |
91,1 |
| Март |
55,9 |
61,0 |
64,5 |
60,47 |
105,3 |
| Апрель |
58,1 |
66,8 |
74,0 |
66,30 |
115,5 |
| Май |
57,4 |
62,7 |
76,3 |
65,47 |
114,1 |
| Июнь |
59,2 |
70,0 |
70,3 |
66,50 |
115,9 |
| Июль |
43,0 |
54,2 |
55,7 |
50,97 |
88,8 |
| Август |
37,8 |
46,6 |
50,8 |
45,07 |
78,5 |
| Сентябрь |
46,0 |
50,4 |
57,3 |
51,23 |
89,3 |
| Октябрь |
51,4 |
54,9 |
58,5 |
54,93 |
95,7 |
| Ноябрь |
55,1 |
60,5 |
62,3 |
59,30 |
103,3 |
| Декабрь |
51,6 |
62,0 |
62,8 |
58,80 |
102,4 |
| Итого |
612,9 |
696,8 |
756,7 |
688,80 |
1200,0 |
2. Определяем общую среднюю за 3 года или 36 месяцев:
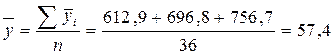 тыс.т. тыс.т.
3. Исчисляются индексы сезонности:
для января – 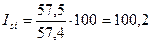 и т.д. и т.д.
Индексы сезонности показывают, что средний объем реализации товара в январе больше среднего объема реализации за весь период на 2 % (100,2-100).
По имеющимся данным построим график сезонной волны – рисунок 3.

Рисунок 3 – График сезонной волны
Задача 7.
По следующим данным, таблица 13, определите индексы себестоимости переменного состава, фиксированного состава и индекс структурных сдвигов. Проанализируйте результаты и сделайте выводы.
Таблица 13
| № предприятия |
Произведено продукции, тыс. шт. |
Себестоимость единицы продукции, тыс. руб. |
| базисный период |
отчетный период |
базисный период |
отчетный период |
| q0
|
q1
|
z0
|
z1
|
| 1 |
470 |
250 |
12,5 |
13,0 |
| 2 |
920 |
940 |
10,1 |
10,3 |
| 3 |
380 |
690 |
4,2 |
5,0 |
Решение:
Для расчета индексов переменного состава, фиксированного состава и структурных сдвигов построим расчетную таблицу 14.
Таблица 14
| № предприятия |
Себестоимость |
Структура |
| z0
|
z1
|
d0
|
d1
|

|
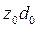
|

|
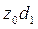
|
| 1 |
12,5 |
13 |
0,27 |
0,13 |
1,73 |
3,32 |
3,45 |
1,66 |
| 2 |
10,1 |
10,3 |
0,52 |
0,50 |
5,15 |
5,25 |
5,35 |
5,05 |
| 3 |
4,2 |
5 |
0,21 |
0,37 |
1,84 |
0,90 |
1,07 |
1,54 |
| Итого
|
1,00
|
1,00
|
8,71
|
9,47
|
9,88
|
8,25
|
Структуру находим по формулам:
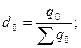  и вносим расчеты в таблицу 14 и вносим расчеты в таблицу 14
Индекс переменного состава равен:

Индекс фиксированного состава равен:Индекс структурных сдвигов находим по формуле:
Вывод: в отчетном периоде по сравнению с базисным себестоимость в среднем по трем предприятиям уменьшилась на 8 % под влиянием изменения самой себестоимости и ее структуры. Под влиянием только себестоимости по каждому предприятию средняя себестоимость увеличилась на 6 %, а под влиянием структуры уменьшилась на 13%.
Список использованных источников
1. Ефимова М.Р. Практикум по общей теории статистики [Текст]: Учебное пособие / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова – М.: Финансы и статистика, 2002. – 320 с.
2. Кречетова М.А. Статистика [Текст]: Учебное пособие / НФИ КемГУ; М.А. Кречетова. – Новокузнецк, 2003. – 91 с.
3. Кречетова М.А. Статистика [Текст]: Метод. Указ. / НФИ КемГУ; М.А. Кречетова. – Новокузнецк, 2004. – 63 с.
4. Практикум по теории статистики [Текст]: Учебное пособие / Под ред. Р.А. Шмойловой – М.: Финансы и статистика, 2001. – 416 с.
5. Рудакова Р.П., Букин Л.Л., Гаврилов В.И. Практикум по статистике [Текст]. – СПб.: Питер, 2007. – 288 с.: ил. – (Серия «Учебное пособие»)
|