контрольная работа
Задание 1
1. Составить уравнение линейной регрессии  , используя МНК, и найти числовые характеристики переменных. , используя МНК, и найти числовые характеристики переменных.
2. Составить уравнение линейной регрессии  , используя матричный метод. , используя матричный метод.
3. Вычислить коэффициент корреляции и оценить полученное уравнение регрессии.
4. Найти оценки параметров  . .
5. Найти параметры нормального распределения для статистик 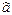 и и  . .
6. Найти доверительные интервалы для 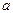 и и  на основании оценок на основании оценок 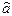 и и 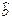 при уровне значимости α = 0,05. при уровне значимости α = 0,05.
7. Вычислить коэффициент детерминации и оценить качество выбранного уравнения регрессии.
Вариант 7
Имеются данные по предприятиям о производительности труда Х
(шт.) и коэффициенте механизации работ Y
(%):
| X
|
20 |
24 |
28 |
30 |
31 |
33 |
34 |
37 |
38 |
40 |
| Y
|
32 |
30 |
36 |
40 |
41 |
47 |
56 |
54 |
60 |
55 |
Задание 2
1. Составить уравнение множественной линейной регрессии y
= a
+ b
1
x
1
+ b
2
x
2
+ ε
в матричной форме, используя МНК, и найти числовые характеристики переменных.
2. Найти оценки параметров а
, b
1
, b
2
, б
².
3. Найти коэффициент детерминации и оценить уравнение регрессивной связи.
4. Оценить статистическую зависимость между переменными.
Вариант 7
Анализируются зависимость объёма продукции предприятия в среднем за год Y
(млн. руб.) от средней численности рабочих Х
1
(тыс. чел.) и Х
2
– средние затраты чугуна за год (млн. т):
| № п/п |
Y
|
Х
1
|
Х
2
|
| 1 |
2,1 |
1,0 |
0,5 |
| 2 |
2,4 |
1,1 |
0,8 |
| 3 |
1,8 |
1,3 |
0,7 |
| 4 |
3,0 |
1,5 |
0,6 |
| 5 |
2,2 |
1,2 |
0,4 |
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
Цель расчетов – не числа,
а понимание.
Г.В. Хемминг
Введение
Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет в науке, особенно в экономике, большую роль. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования тесноты, вида и формы причинных влияний широко применяется корреляционный и регрессионный анализ, позволяющий получить все необходимые оценки существующей статистической связи различных признаков. Однако методы этого анализа очень сложны, требуют для своего изучения высокого уровня математической подготовки, отчетливого понимания всего хода вычислительного процесса и интерпретации результатов. Не имея достаточной квалификации, опыта в применении методов корреляционного и регрессионного анализа, трудно получить достоверные и правильные с математической точки зрения результаты. Наиболее важным и самым первым этапом проведения анализа статистической связи специальными методами является теоретическое объяснение найденных причинно-следственных связей, их объективного, не случайного характера. На этом этапе хорошую помощь может оказать проведение аналитической группировки, показывающей общий характер связи между изучаемыми признаками.
Целью выполнения расчетно-графической работы (РГР) является первоначальное знакомство студентов с методами описания статистической совокупности, с методами изучения статистической связи и с интерпретацией результатов. В ходе выполнения РГР предполагается изучение метода средних величин как способа описания статистической совокупности из трех методов изучения статистической связи. Первый – метод группировок, позволяющий установить сам факт наличия статистической связи, второй –метод корреляционного анализа, устанавливающий степень тесноты связи, и третий – метод регрессионного анализа, показывающий форму связи между изучаемыми признаками в статистической совокупности. В связи с большим объемом вычислительной работы рекомендуется выполнение всех расчетов с использованием персонального компьютера и применением электронных таблиц, изученных студентами в курсе информатики. Возможно использование специализированных программных продуктов для статистической обработки данных, таких как SPSS, Statgraphics, Stadia и др.
Требования к оформлению РГР
Расчетно-графическая работа выполняется на листах бумаги формата А4 рукописным или машинописным способом с последующим обязательным сшиванием оформленной работы. Текст работы должен включать номер шифра задания, таблицы с исходными данными, основные расчетные формулы и результаты расчета по ним. Изложение материала сопровождается построением таблиц, отражающих результаты аналитической группировки и других расчетов, гистограммами и диаграммами рассеяния, другими материалами, позволяющими показать особенности статистической связи между изучаемыми признаками и сопоставить между собой все четыре набора исходных статистических данных. Выполнение работы завершается формулировкой выводов, опирающихся на результаты проведенных расчетов.
Исходные данные
В результате обследования в четырех цехах предприятия станков четырех разных типов, выполняющих одну и ту же операцию, были получены статистические данные о возрасте оборудования и об эксплуатационных расходах, связанных с работой этих станков. Возраст оборудования – целое число, для станка проработавшего менее одного года, – 1; от 1 года до 2 лет –2 и т.д. Эксплуатационные расходы фиксировались для каждого станка нарастающим итогом с начала года до момента проведения обследования. В результате выполняемой работы предполагалось определить, у какого типа станков наиболее низкие эксплуатационные расходы, как с возрастом станка меняется величина эксплуатационных расходов, с тем чтобы в последующем, при планируемой реорганизации и расширении станочного парка предприятия, произвести замену оборудования наиболее экономичным с точки зрения величины эксплуатационных расходов. Исходные данные для анализа представлены в табл. 2 – 5. Необходимо отметить, что статистические данные таблиц являются условными, значительно более удобными для выполнения учебных расчетов, чем данные реальных наблюдений, однако эти условные данные полностью отражают те процессы и статистические закономерности, которые наблюдаются на реальном промышленном предприятии.
Выбор исходных данных
Исходные данные выбираются из табл. 2–5. Студент приступая к выполнению РГР, выбирает из каждой таблицы только одну ее треть (один из выбранных вариантов), пользуясь четырехзначным шифром. Вариант и шифр выбирается по заглавной букве фамилии студента (табл. 1). Например, студент получил шифр 1231. Это значит, что из табл. 2 для анализа выбирается первая ее треть, из табл. 3 – вторая треть, из табл. 4 – третья треть и табл. 5 – первая треть.
Таблица 1
| Начальная буква фамилии |
Номер варианта |
Шифр |
| А |
1 |
1111 |
| Б |
2 |
1122 |
| В |
3 |
1133 |
| Г |
4 |
1222 |
| Д |
5 |
1333 |
| Е, ё |
6 |
1212 |
| Ж |
7 |
1313 |
| З |
8 |
1323 |
| И |
9 |
1232 |
| К |
10 |
1231 |
| Л |
11 |
1321 |
| М |
12 |
2222 |
| Н |
13 |
2112 |
| О |
14 |
2332 |
| П |
15 |
2133 |
| Р |
16 |
2311 |
| С |
17 |
2213 |
| Т |
18 |
2321 |
| У |
19 |
2312 |
| Ф |
20 |
2122 |
| Х |
21 |
3333 |
| Ц |
22 |
3113 |
| Ч |
23 |
3223 |
| Ш |
24 |
3311 |
| Щ |
25 |
3322 |
| Э |
26 |
3123 |
| Ю |
27 |
3213 |
| Я |
28 |
3211 |
Таблица 2
| Вариант 1 |
Вариант 2 |
Вариант 3 |
| № |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
| 1 |
10 |
22.0 |
36 |
5 |
18.4 |
71 |
18 |
28.4 |
| 2 |
12 |
24.1 |
37 |
5 |
17.6 |
72 |
18 |
29.6 |
| 3 |
7 |
20.8 |
38 |
5 |
18.0 |
73 |
18 |
29.8 |
| 4 |
13 |
24.5 |
39 |
11 |
20.1 |
74 |
7 |
20.4 |
| 5 |
15 |
26.6 |
40 |
16 |
28.5 |
75 |
19 |
29.6 |
| 6 |
6 |
19.4 |
41 |
16 |
27.4 |
76 |
4 |
18.0 |
| 7 |
10 |
22.5 |
42 |
9 |
20.6 |
77 |
20 |
29.4 |
| 8 |
6 |
19.6 |
43 |
17 |
29.6 |
78 |
14 |
26.2 |
| 9 |
4 |
19.9 |
44 |
3 |
16.4 |
79 |
19 |
29.0 |
| 10 |
4 |
19.0 |
45 |
3 |
16.0 |
80 |
16 |
27.2 |
| 11 |
8 |
21.0 |
46 |
15 |
26.3 |
81 |
1 |
15.1 |
| 12 |
8 |
21.1 |
47 |
6 |
20.0 |
82 |
12 |
25.9 |
| 13 |
8 |
21.5 |
48 |
10 |
27.9 |
83 |
12 |
26.6 |
| 14 |
13 |
25.0 |
49 |
10 |
24.4 |
84 |
5 |
19.1 |
| 15 |
7 |
20.9 |
50 |
10 |
23.1 |
85 |
5 |
19.2 |
| 16 |
14 |
24.0 |
51 |
11 |
24.0 |
86 |
6 |
18.8 |
| 17 |
14 |
24.4 |
52 |
2 |
17.0 |
87 |
6 |
18.9 |
| 18 |
9 |
22.7 |
53 |
1 |
16.1 |
88 |
17 |
27.0 |
| 19 |
14 |
27.0 |
54 |
17 |
28.2 |
89 |
17 |
28.0 |
| 20 |
12 |
25.0 |
55 |
2 |
16.5 |
90 |
10 |
23.3 |
| 21 |
12 |
25.0 |
56 |
7 |
22.5 |
91 |
6 |
17.5 |
| 22 |
15 |
26.7 |
57 |
7 |
21.5 |
92 |
9 |
21.9 |
| 23 |
10 |
22.6 |
58 |
17 |
28.8 |
93 |
5 |
18.2 |
| 24 |
3 |
17.3 |
59 |
13 |
27.0 |
94 |
13 |
26.8 |
| 25 |
3 |
18.0 |
60 |
5 |
18.9 |
95 |
4 |
17.5 |
| 26 |
9 |
22.5 |
61 |
15 |
25.5 |
96 |
14 |
25.7 |
| 27 |
2 |
16.0 |
62 |
8 |
20.4 |
97 |
7 |
20.5 |
| 28 |
9 |
23.6 |
63 |
12 |
25.4 |
98 |
6 |
18.5 |
| 29 |
7 |
19.5 |
64 |
14 |
25.8 |
99 |
10 |
23.5 |
| 30 |
7 |
19.4 |
65 |
9 |
20.8 |
100 |
8 |
22.2 |
| 31 |
1 |
15.5 |
66 |
15 |
28.4 |
101 |
8 |
24.9 |
| 32 |
13 |
25.2 |
67 |
11 |
23.3 |
102 |
12 |
23.7 |
| 33 |
13 |
26.3 |
68 |
11 |
23.7 |
103 |
11 |
24.4 |
| 34 |
16 |
29.4 |
69 |
16 |
27.0 |
104 |
9 |
21.7 |
| 35 |
8 |
19.9 |
70 |
7 |
20.0 |
105 |
7 |
22.0 |
Таблица 3
| Вариант 1 |
Вариант 2 |
Вариант 3 |
| № |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
| 1 |
8 |
24.1 |
36 |
10 |
24.6 |
71 |
11 |
25.4 |
| 2 |
4 |
22.1 |
37 |
20 |
29.7 |
72 |
16 |
27.9 |
| 3 |
13 |
26.8 |
38 |
12 |
26.5 |
73 |
13 |
27.4 |
| 4 |
6 |
23.0 |
39 |
15 |
28.3 |
74 |
16 |
28.3 |
| 5 |
14 |
27.3 |
40 |
16 |
27.6 |
75 |
13 |
27.8 |
| 6 |
15 |
28.0 |
41 |
3 |
21.3 |
76 |
19 |
29.5 |
| 7 |
10 |
25.4 |
42 |
7 |
23.2 |
77 |
17 |
29.9 |
| 8 |
16 |
28.5 |
43 |
18 |
28.2 |
78 |
16 |
28.1 |
| 9 |
19 |
29.2 |
44 |
15 |
27.0 |
79 |
6 |
23.3 |
| 10 |
7 |
26.0 |
45 |
12 |
26.6 |
80 |
13 |
26.3 |
| 11 |
5 |
21.7 |
46 |
4 |
21.7 |
81 |
2 |
22.2 |
| 12 |
7 |
25.2 |
47 |
11 |
28.0 |
82 |
6 |
23.7 |
| 13 |
3 |
23.6 |
48 |
15 |
26.3 |
83 |
6 |
23.6 |
| 14 |
20 |
30.0 |
49 |
8 |
24.5 |
84 |
2 |
21.3 |
| 15 |
12 |
25.8 |
50 |
3 |
20.8 |
85 |
10 |
25.7 |
| 16 |
14 |
28.8 |
51 |
17 |
29.2 |
86 |
19 |
28.6 |
| 17 |
12 |
25.1 |
52 |
17 |
27.8 |
87 |
18 |
28.8 |
| 18 |
18 |
29.1 |
53 |
19 |
30.0 |
88 |
6 |
21.6 |
| 19 |
11 |
26.1 |
54 |
18 |
29.9 |
89 |
6 |
20.6 |
| 20 |
9 |
24.5 |
55 |
9 |
25.7 |
90 |
17 |
28.7 |
| 21 |
16 |
29.1 |
56 |
9 |
23.4 |
91 |
8 |
24.7 |
| 22 |
2 |
20.8 |
57 |
4 |
20.7 |
92 |
1 |
21.1 |
| 23 |
8 |
21.2 |
58 |
12 |
27.3 |
93 |
8 |
24.8 |
| 24 |
14 |
26.3 |
59 |
12 |
27.1 |
94 |
13 |
27.2 |
| 25 |
16 |
26.1 |
60 |
9 |
25.3 |
95 |
3 |
21.2 |
| 26 |
5 |
22.4 |
61 |
14 |
27.0 |
96 |
6 |
22.2 |
| 27 |
18 |
29.6 |
62 |
4 |
20.2 |
97 |
14 |
27.5 |
| 28 |
1 |
20.0 |
63 |
11 |
27.6 |
98 |
14 |
27.6 |
| 29 |
10 |
25.9 |
64 |
8 |
23.2 |
99 |
4 |
22.7 |
| 30 |
9 |
27.0 |
65 |
2 |
21.2 |
100 |
11 |
24.8 |
| 31 |
20 |
29.3 |
66 |
10 |
26.8 |
101 |
10 |
25.0 |
| 32 |
12 |
24.2 |
67 |
7 |
23.8 |
102 |
7 |
22.7 |
| 33 |
15 |
29.9 |
68 |
18 |
27.1 |
103 |
9 |
24.8 |
| 34 |
15 |
29.2 |
69 |
5 |
22.9 |
104 |
5 |
24.7 |
| 35 |
11 |
24.3 |
70 |
17 |
28.5 |
105 |
13 |
24.7 |
Таблица 4
| Вариант 1 |
Вариант 2 |
Вариант 3 |
| № |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
| 1 |
9 |
26.5 |
36 |
14 |
31.0 |
71 |
18 |
31.8 |
| 2 |
12 |
29.2 |
37 |
9 |
27.6 |
72 |
10 |
28.0 |
| 3 |
8 |
26.0 |
38 |
7 |
26.1 |
73 |
2 |
20.5 |
| 4 |
6 |
28.0 |
39 |
1 |
20.7 |
74 |
7 |
24.2 |
| 5 |
16 |
31.0 |
40 |
10 |
28.9 |
75 |
16 |
34.6 |
| 6 |
20 |
35.0 |
41 |
10 |
28.7 |
76 |
14 |
28.7 |
| 7 |
15 |
30.9 |
42 |
6 |
24.8 |
77 |
3 |
20.1 |
| 8 |
15 |
32.3 |
43 |
6 |
24.5 |
78 |
13 |
28.8 |
| 9 |
17 |
32.5 |
44 |
8 |
24.5 |
79 |
13 |
30.1 |
| 10 |
19 |
34.2 |
45 |
17 |
34.0 |
80 |
13 |
29.8 |
| 11 |
13 |
33.1 |
46 |
3 |
22.8 |
81 |
6 |
24.3 |
| 12 |
19 |
34.9 |
47 |
7 |
26.3 |
82 |
9 |
27.8 |
| 13 |
9 |
27.3 |
48 |
3 |
23.3 |
83 |
6 |
25.2 |
| 14 |
6 |
27.1 |
49 |
11 |
29.1 |
84 |
12 |
28.2 |
| 15 |
10 |
27.0 |
50 |
11 |
29.3 |
85 |
10 |
27.5 |
| 16 |
14 |
30.4 |
51 |
12 |
30.0 |
86 |
9 |
24.9 |
| 17 |
5 |
24.0 |
52 |
14 |
31.3 |
87 |
7 |
23.6 |
| 18 |
17 |
33.0 |
53 |
5 |
22.3 |
88 |
8 |
23.8 |
| 19 |
7 |
29.6 |
54 |
5 |
22.2 |
89 |
8 |
26.5 |
| 20 |
7 |
25.0 |
55 |
5 |
23.1 |
90 |
11 |
27.8 |
| 21 |
17 |
25.2 |
56 |
18 |
33.3 |
91 |
14 |
29.9 |
| 22 |
11 |
33.4 |
57 |
11 |
27.6 |
92 |
5 |
23.7 |
| 23 |
11 |
28.5 |
58 |
8 |
24.1 |
93 |
15 |
32.1 |
| 24 |
3 |
31.0 |
59 |
6 |
23.8 |
94 |
1 |
20.5 |
| 25 |
17 |
22.2 |
60 |
2 |
22.0 |
95 |
4 |
22.5 |
| 26 |
16 |
33.8 |
61 |
4 |
23.4 |
96 |
7 |
22.8 |
| 27 |
10 |
29.5 |
62 |
4 |
23.7 |
97 |
12 |
28.6 |
| 28 |
8 |
27.3 |
63 |
4 |
24.7 |
98 |
8 |
26.8 |
| 29 |
8 |
26.2 |
64 |
15 |
32.0 |
99 |
14 |
30.2 |
| 30 |
15 |
26..3 |
65 |
16 |
32.6 |
100 |
13 |
29.5 |
| 31 |
13 |
31.7 |
66 |
16 |
34.7 |
101 |
9 |
26.3 |
| 32 |
13 |
31.7 |
67 |
18 |
33.9 |
102 |
16 |
31.8 |
| 33 |
2 |
21.1 |
68 |
18 |
34.9 |
103 |
20 |
34.5 |
| 34 |
5 |
24.4 |
69 |
19 |
34.9 |
104 |
12 |
29.0 |
| 35 |
5 |
23.0 |
70 |
20 |
34.0 |
105 |
13 |
30.5 |
Таблица 5
| Вариант 1 |
Вариант 2 |
Вариант 3 |
| № |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
№ |
Возраст |
Экспл. расходы, тыс.руб. |
| 1 |
8 |
19.1 |
36 |
8 |
18.3 |
71 |
7 |
12.1 |
| 2 |
10 |
21.0 |
37 |
2 |
11.0 |
72 |
7 |
18.3 |
| 3 |
11 |
25.0 |
38 |
14 |
32.1 |
73 |
7 |
18.4 |
| 4 |
4 |
12.1 |
39 |
10 |
18.2 |
74 |
11 |
24.0 |
| 5 |
5 |
15.0 |
40 |
18 |
29.0 |
75 |
11 |
21.9 |
| 6 |
8 |
19.1 |
41 |
18 |
29.5 |
76 |
12 |
23.5 |
| 7 |
6 |
16.9 |
42 |
4 |
14.2 |
77 |
13 |
22.1 |
| 8 |
7 |
18.1 |
43 |
6 |
16.0 |
78 |
8 |
17.7 |
| 9 |
9 |
20.0 |
44 |
18 |
29.1 |
79 |
11 |
21.5 |
| 10 |
11 |
20.5 |
45 |
10 |
19.2 |
80 |
12 |
24.0 |
| 11 |
12 |
20.2 |
46 |
5 |
14.1 |
81 |
9 |
19.1 |
| 12 |
8 |
17.9 |
47 |
12 |
21.9 |
82 |
19 |
26.0 |
| 13 |
4 |
13.5 |
48 |
12 |
23.0 |
83 |
14 |
20.2 |
| 14 |
10 |
20.7 |
49 |
12 |
28.0 |
84 |
13 |
25.0 |
| 15 |
14 |
25.0 |
50 |
3 |
11.9 |
85 |
2 |
11.5 |
| 16 |
14 |
25.1 |
51 |
7 |
16.2 |
86 |
11 |
21.0 |
| 17 |
6 |
16.4 |
52 |
4 |
14.3 |
87 |
2 |
11.5 |
| 18 |
15 |
26.0 |
53 |
3 |
12.5 |
88 |
5 |
13.9 |
| 19 |
15 |
25.4 |
54 |
3 |
15.9 |
89 |
13 |
25.5 |
| 20 |
7 |
18.2 |
55 |
13 |
23.9 |
90 |
7 |
17.1 |
| 21 |
15 |
23.1 |
56 |
13 |
24.1 |
91 |
15 |
24.3 |
| 22 |
9 |
19.8 |
57 |
5 |
16.0 |
92 |
16 |
28.0 |
| 23 |
9 |
19.8 |
58 |
8 |
16.1 |
93 |
9 |
21.2 |
| 24 |
9 |
17.9 |
59 |
3 |
10.0 |
94 |
16 |
26.8 |
| 25 |
16 |
26.0 |
60 |
1 |
10.0 |
95 |
2 |
12.3 |
| 26 |
6 |
15.1 |
61 |
1 |
10.1 |
96 |
1 |
11.2 |
| 27 |
17 |
28.1 |
62 |
7 |
17.6 |
97 |
5 |
16.4 |
| 28 |
10 |
20.1 |
63 |
19 |
29.9 |
98 |
4 |
13.2 |
| 29 |
5 |
15.5 |
64 |
6 |
16.1 |
99 |
13 |
23.0 |
| 30 |
7 |
16.1 |
65 |
20 |
29.1 |
100 |
14 |
24.4 |
| 31 |
17 |
29.0 |
66 |
9 |
18.6 |
101 |
20 |
29.8 |
| 32 |
14 |
24.0 |
67 |
20 |
30.0 |
102 |
17 |
27.6 |
| 33 |
11 |
22.9 |
68 |
10 |
24.5 |
103 |
18 |
27.4 |
| 34 |
17 |
27.0 |
69 |
12 |
22.3 |
104 |
10 |
19.8 |
| 35 |
3 |
12.0 |
70 |
11 |
26.0 |
105 |
6 |
15.4 |
Порядок выполнения работы
В соответствии со своим вариантом задания на расчетно-графическую работу студент должен выполнить следующую последовательность действий:
1. По каждому набору данных, содержащему значения двух взаимосвязанных статистических признаков (возраст оборудования и эксплуатационные расходы), определить средний возраст оборудования, средниеэксплуатационные расходы, среднее квадратическое отклонение для каждого статистического признака. Определить медиану возраста оборудования для каждого набора данных. Сравнить между собой средние значения для всех четырех наборов исходных данных, построив таблицу, позволяющую произвести такое сравнение. Сделать выводы о том, на каком объекте наблюдения старше оборудование и где наиболее высоки эксплуатационные расходы.
2. Произвести аналитическую группировку статистических данных, выбрав в качестве факторного признака возраст оборудования, результативного признака – эксплуатационные расходы. Для проведения такой группировки рекомендуется создать четыре группы станков по возрасту: от 1 года до 5, от 6 до 10, от 2 до 15, от 15 до 20 (станков старше 20 лет нет ни в одном цехе). В каждой образованной по возрасту группе найти средние по группе эксплуатационные расходы. Результаты группировки представить в табличном виде. Макеты необходимых таблиц приведены в приложении. Эти же данные представить в виде набора из четырех гистограмм, показывающих распределение оборудования по возрасту на каждом из объектов наблюдения. По результатам построения таблиц и гистограмм сделать выводы. Определить моду возраста оборудования для каждого набора данных расчетным путем и графически.
3. Для каждого набора данных определить коэффициент Фехнера, построить поле корреляции, рассчитать коэффициент корреляции и определить, для какого цеха наблюдается более тесная связь между возрастом оборудования и величиной эксплуатационных издержек. Для каждого объекта получить уравнение линии регрессии, показывающей характер связи между возрастом оборудования и эксплуатационными расходами (связь считать прямолинейной). По полученным уравнениям сделать выводы о том, на каком объекте наблюдения быстрее возрастают с возрастом эксплуатационные расходы.
Указания к выполнению РГР
Средние величины
Для описания статистических данных одним из наиболее простых и эффективных методов является метод средних величин. По отдельным значениям статистического признака х
i
, полученным в результате наблюдения, возможно получить среднюю величину, рассчитываемую по различным правилам и характеризующую одним лишь числом всю изучаемую совокупность данных. Для выполнения РГР используется среднее арифметическое, вычисляемое по правилу
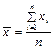 , ,
где х
i
– отдельные значения признака, полученные в результате наблюдения; n
– общее число наблюдений.
Для описания того, как далеко отдельные значения признака х
i
отстоят от полученного среднего арифметического 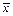 или, иными словами, для описания рассеяности изучаемой совокупности, используют величину, называемую средним квадратическим отклонением. Величина среднего квадратического отклонения рассчитывается по формуле или, иными словами, для описания рассеяности изучаемой совокупности, используют величину, называемую средним квадратическим отклонением. Величина среднего квадратического отклонения рассчитывается по формуле
 , ,
где х
i
– отдельные значения признака; 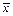 – среднее арифметическое; n
–общее число наблюдений. – среднее арифметическое; n
–общее число наблюдений.
В случае, когда необходимо сравнить между собой две статистические совокупности и сказать, какая из них рассеяна меньше и обладает соответственно большей однородностью наблюдений, используют характеристику рассеяния, называемую коэффициентом вариации. Пусть необходимо сравнить две статистические совокупности:
х
со значениями признака х
i
 ; ;
У
со значениями признака у
i
 . .
Для нахождения коэффициентов вариации предварительно определяются:
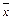 – среднее арифметическое для совокупности X
; – среднее арифметическое для совокупности X
;
 – среднее арифметическое для совокупности У
; – среднее арифметическое для совокупности У
;
Sx
– среднее квадратическое отклонение для совокупности X
;
Sy
– среднее квадратическое отклонение для совокупности У
.
Коэффициенты вариации находятся по формулам:
 – коэффициент вариации для совокупности х
; – коэффициент вариации для совокупности х
;
 – коэффициент вариации для совокупности У
. – коэффициент вариации для совокупности У
.
Коэффициент вариации позволяет сопоставить между собой статистические совокупности, у которых значения признака измеряются в разных единицах измерения. Так, например, можно сравнить, что на предприятии изменяется больше – величина заработной платы рабочих или производительность труда. Чем меньше коэффициент вариации, тем более однородной является изучаемая статистическая совокупность. Принято считать, что при коэффициенте вариации более 10 процентов изучаемая совокупность не является однородной и для ее достоверного описания необходимо по какому-либо признаку выделять группы, обладающие большей однородностью. Рассматривая, например, среднюю заработную плату рабочих цеха, рассчитывая коэффициент вариации заработной платы и получив его достаточно большим (много больше 10 процентов), можно попытаться выделить в изучаемой совокупности две группы рабочих: основные рабочие и вспомогательные. По каждой из этих групп определяется средняя заработная плата, вариация признаков в каждой группе меньше (меньше должны быть коэффициенты вариации), и полученные средние более достоверно будут характеризовать изучаемую совокупность статистических данных.
Еще одной из характеристик изучаемой совокупности является медиана Ме
– число, делящее упорядоченную по возрастанию совокупность значений признака на две равные части, у одной части значение признака меньше медианы, у другой части – больше.
Пример
: значения признака выражены числами 2, 2, 4, 5, 7, 9, 10. Медианой является число 5, три значения признака в этой совокупности меньше 5, три значения больше 5. В случае четного числа значений признака:
2, 2, 4, 5, 7, 9, 10, 11 медианой является число  , делящее рассматриваемую совокупность на 2 части. При этом четыре значения признака меньше 6, четыре значения – больше. , делящее рассматриваемую совокупность на 2 части. При этом четыре значения признака меньше 6, четыре значения – больше.
В РГР предлагается определить для каждого объекта наблюдения медиану возраста оборудования – возраст, который превысила уже половина станочного парка.
Метод группировок
Для выяснения закономерностей, существующих в изучаемой совокупности, и для установления возможной связи между различными признаками используют метод группировок. Группировка – процесс разделения статистической совокупности на группы, однородные в каком-либо отношении либо имеющие одинаковые или близкие значения группировочного признака. Так, например, всю совокупность станочного парка предприятия можно разбить на группы по признаку "возраст", образовав группы станков: от 1 до 5 лет, от 6 до 10, от 2 до 15 и от 16 до 20 лет. Здесь в качестве группировочного признака выбран возраст и созданы группы, имеющие близкое значение группировочного признака. Подсчитав число станков, попавших в каждую группу, можно сделать выводы о распределении станков по возрасту. По каждой выделенной группе далее можно рассчитать значения других признаков, характеризующих станки. Например – среднее по группе число часов простоев за год, средние по группе эксплуатационные расходы, общее число текущих ремонтов за период и др. Выполнив подобные расчеты, можно посмотреть, как с увеличением возраста станков от группы к группе меняется второй признак.
Группировки подобного рода, сопоставляющие два признака, называются аналитическими. Тот признак, который оказывает влияние на другой, называется факторным, а тот, на котором отражается воздействие факторного признака, называется результативным. Если при увеличении факторного признака результативный увеличивается, то говорят о наличии прямой связи между двумя изучаемыми признаками, если при увеличении факторного признака результативный уменьшается, то говорят об обратной связи. Однако проведение аналитической группировки позволяет лишь установить факт наличия связи, а степень тесноты связи, ее форму изучают более сложными методами, изложенными в следующем разделе.
Результаты выполнения группировки, показывающей структуру станочного парка по возрасту, удобно представить в следующем виде (табл. 6).
Таблица 6
Распределение станочного парка по возрасту
| Группы по возрасту, лет |
Число станков в группе, шт |
В процентах к итогу |
от 1 до 5
|
5
|
14.29
|
от 6 до 10
|
16
|
45.71
|
от 2 до 15
|
10
|
28.57
|
от 16 до 20
|
4
|
11.43
|
Графический способ представления этих же данных – гистограмма. Гистограмма строится в прямоугольной системе координат, где по оси абсцисс откладываются отрезки, изображающие, в каких пределах изменяются значения изучаемого признака, а по оси ординат на отложенных отрезках вплотную друг к другу строятся прямоугольники, показывающие, сколько значений признака при его группировке попадают на тот или иной интервал. При этом площади прямоугольников изображаются пропорционально количеству значений признака, попавшему на каждый из интервалов, отложенных по оси абсцисс. В случае равной величины интервалов, откладываемых по оси X
, высоты прямоугольников изображаются пропорционально количеству значений признака, попавших на каждый интервал.
Определение моды
Мода (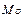 ) – наиболее часто встречающееся значение признака в совокупности. ) – наиболее часто встречающееся значение признака в совокупности.
 , ,
где: ХМО
– начало модального интервала; i
– величина интервала; fMO
–частота, соответствующая модальному интервалу; fMO
–1
– предмодальная частота; fMO
+1
– послемодальная частота.
Графически мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.
Пример построения гистограммы, основанный на данных из табл. 6, и моды представлен на рис.1.
Корреляция
Между двумя статистическими признаками могут наблюдаться два вида взаимосвязи. Первый вид – функциональная взаимосвязь, при которой значения результативного (зависимого) признака У
полностью определяются изменениями факторного (независимого) признака X
. В случае функциональной связи можно записать математическое выражение, показывающее характер, форму связи между двумя признаками. Так, например, можно записать уравнение функциональной связи, известное из курса физики, между скоростью падения тела, опущенного с некоторой высоты, и временем полета:

Рис. 1. Гистограмма
 , ,
где v –
скорость падения; t
– время падения; g
– ускорение свободного падения. По этому уравнению, зная время полета (факторный признак), всегда можно найти скорость падающего тела (результативный признак). Множество лабораторных экспериментов подтверждают записанное уравнение функциональной связи. Однако также хорошо известно, что лист дерева и камень падают с одной и той же высоты с разной скоростью. Парашютист приземляется на аэродроме всегда примерно с одинаковой скоростью, независимо от высоты, с которой произошел прыжок (значит, независимо и от продолжительности прыжка). В показанных примерах на падающее тело действует множество других факторов, главный из которых –сопротивление воздуха. В таких условиях, когда на связь между факторным и результативным признаком воздействует множество различных факторов, затруднительно установить функциональную связь между признаками. В подобных случаях изменение результативного признака У
обусловлено влиянием факторного признака х
лишь частично, однако это влияние вполне заметно. Это другой вид статистической связи – корреляционная связь.
Общая форма корреляционной связи представляется выражением:
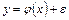 , ,
где φ
(х
) – функция, представляющая форму связи между факторным и результативным признаками; ε
– элемент, отражающий влияние всех неучтенных факторов.
При корреляционной связи между статистическими признаками одному и тому же значению факторного признака соответствуют различные значения результативного признака, однако есть и общая тенденция, показывающая, что в среднем при увеличении факторного признака происходит соответствующее увеличение или уменьшение, в среднем, результативного признака. Это среднее изменение и показывает функция φ
(х
).
Если рассматривать связь между возрастом оборудования и эксплуатационными расходами, связанными с этим оборудованием, то такую связь можно заметить, проведя аналитическую группировку (первая часть РГР): при увеличении возраста станков в среднем увеличиваются и эксплуатационные расходы. Однако по статистическим данным, представленным в табл. 2 – 5, видно, что в каждой таблице есть данные о станках с одинаковым возрастом, но со значительно различающимися эксплуатационными расходами, так как на величину этих расходов влияет не только возраст, но и ряд других факторов: частота и качество предыдущих технических обслуживаний, интенсивность эксплуатации станка, частота нарушений рекомендуемых режимов работы и др. Для одного типа станков определенному возрасту соответствует бόльшая вариация величины эксплуатационных расходов, другому типу станков – меньшая. Таким образом, для каждой из четырех групп станков, представленных таблицами, существует разная степень тесноты связи между возрастом и эксплуатационными расходами.
К простейшим показателям тесноты связи относят коэффициент корреляции знаков – коэффициент Фехнера. Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних.
Для его расчета вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязи пар признаков.
 , ,
где Кф
– коэффициент Фехнера; na
– число совпадений знаков отклонений индивидуальных величин от средней; nв
– число несовпадений знаков отклонений.
Коэффициент Фехнера может принимать различные значения в пределах от –1 до +1. Если коэффициент близок к +1, то можно предположить наличие прямой связи, если –1, то наличие обратной связи.
Степень тесноты связи в статистике измеряют с помощью специального показателя, называемого коэффициентом корреляции:
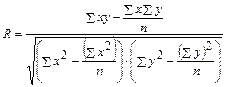 , ,
где х
– значения факторного признака; у
– значения результативного признака; n
– общее число наблюдений.
Предполагается что в формуле суммирование производится для всех значений признаков х
i
и у
i
,  . Эти обозначения опущены для упрощения записи. . Эти обозначения опущены для упрощения записи.
Представленный коэффициент корреляции предполагает, что между х
и у
существует связь, которая является прямолинейной. В случае, когда связь между признаками нелинейная, используются другие статистические показатели для описания тесноты связи, рассмотрение которых не входит в задачу настоящих методических указаний.
Значения коэффициента корреляции могут изменяться от –1 до 1. В случае R
=1 между признаками существует полная функциональная связь, причем связь прямая – при увеличении х
увеличивается и у
. При R
= –1 –связь функциональная и обратная (при увеличении х
у
уменьшается). В случае, когда R
=0, между изучаемыми признаками отсутствует какая-либо связь. Однако при изучении статистической связи очень редко появляются предельные значения коэффициента корреляции, поэтому полученным промежуточным значениям коэффициента корреляции дается качественная оценка: при R
> 0.7 – теснота связи между х
и у
считается высокой, при R
> 0.9 – очень высокой. Чем ближе коэффициент корреляции к 1 или –1, тем более тесной является связь между статистическими признаками. Получив в РГР коэффициенты корреляции для всех четырех групп станков, можно установить, для какой группы наблюдается более тесная связь между возрастом станков и величиной эксплуатационных расходов.
Вторым этапом изучения статистической связи вслед за определением степени тесноты связи с помощью коэффициента корреляции идет этап установления формы связи или вида функции φ
(х
), объясняющей основную закономерность влияния факторного признака х
на результативный признак у
.
Под формой статистической связи понимают ту тенденцию, которая проявляется в изменении изучаемого результативного признака в связи с изменением факторного признака. Форму связи можно попытаться установить, построив в прямоугольной системе координат все множество пар значений признаков (х
i
, у
i
),  . По оси абсцисс откладываются значения факторного признака х
, по оси ординат – значения признака у
. Такое графическое построение называется полем корреляции или диаграммой рассеяния, пример построения представлен на рис. 2. По характеру расположения точек на координатной плоскости можно судить о характере статистической связи. Если наблюдается тенденция равномерного возрастания или убывания значений признака, то связь называется прямолинейной. При тенденции неравномерного изменения значений зависимость носит название криволинейной. . По оси абсцисс откладываются значения факторного признака х
, по оси ординат – значения признака у
. Такое графическое построение называется полем корреляции или диаграммой рассеяния, пример построения представлен на рис. 2. По характеру расположения точек на координатной плоскости можно судить о характере статистической связи. Если наблюдается тенденция равномерного возрастания или убывания значений признака, то связь называется прямолинейной. При тенденции неравномерного изменения значений зависимость носит название криволинейной.
Линия на графике (см. рис. 2), изображающая тенденцию в изменении результативного признака при возрастании факторного, называется линией регрессии. В случае прямолинейной связи линия регрессии ищется в виде уравнения прямой линии:
 , ,
где у
– теоретические значения результативного признака, образующие прямую линию; а0
, а1
– параметры уравнения; х
– значения факторного признака.
При попытках установления криволинейной связи может использоваться достаточно широкий класс математических функций:
1) 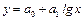 – полулогарифмическая; – полулогарифмическая;
2)  –
показательная; –
показательная;
3) 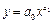 – степенная; – степенная;
4) 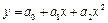 – параболическая; – параболическая;
5)  – гиперболическая и др. – гиперболическая и др.
Во всех случаях расчет параметров уравнения производится методом наименьших квадратов. В основу метода положено требование минимальности отклонения теоретических значений у’
i
от эмпирических (полученных в результате наблюдения) значений признака у
i
при одном и том же значении х
i
. Это требование в математических обозначениях записывается следующим образом:
 . .
Подставляя вместо теоретических значений 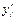 их запись через параметры а0
и а1
, получаем их запись через параметры а0
и а1
, получаем
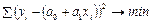 . .
В этом выражении известны все х
i
и у
i
, полученные в результате наблюдения, неизвесты лишь а0
и а1
. Полученная функция двух переменных а0
и а1
имеет минимум, когда частные производные  и и  одновременно равны 0. Произведя дифференцирование по а0
и а1
, получаем систему двух уравнений с двумя неизвестными, решив которую, получим выражение для нахождения коэффициентов а0
и а1
: одновременно равны 0. Произведя дифференцирование по а0
и а1
, получаем систему двух уравнений с двумя неизвестными, решив которую, получим выражение для нахождения коэффициентов а0
и а1
:
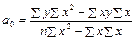 , ,
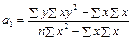 , ,
где n
– общее число наблюдений; х
, у
– значения признаков, полученные в результате наблюдения.

Рис. 2. Диаграмма рассеяния и линия регрессии
Рассмотрим значения коэффициентов, полученных при расчете. Параметр а1
в уравнении регрессии называется коэффициентом регрессии. Коэффициент регрессии показывает среднее изменение результативного признака у
при увеличении факторного признака х
на единицу. Например, получив уравнение прямолинейной связи
у = 20.5 + 1.3х,
можно утверждать, что с увеличением признака х
на единицу у
увеличивается в среднем на 1.3 единицы. По отношению к статистическим данным, представленным в задании на РГР, такое уравнение показывает, что при увеличении возраста станка на один год эксплуатационные расходы возрастают в среднем на 1.3 тысячи рублей. Большее значение коэффициента регрессии будет свидетельствовать и о более быстром нарастании величины эксплуатационных расходов с возрастом. В случае обратной связи коэффициент регрессии получается отрицательным.
Другой коэффициент а0
носит название свободного параметра и какого-либо особого смыслового значения не несет.
Установлением вида статистической связи в виде прямой линии завершается выполнение расчетно-графической работы.
Библиографический список
1. Дружинин Н.К. Основные математико-статистические методы в экономических исследованиях. – М.: Статистика,1968.
2. Общая теория статистики Под ред. А.Я. Боярского, Г.А. Громыко. – 2-е изд. – М.: Изд-во Моск. ун-та, 1985.
3. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник /А.М. Харламов, О.Э. Башина, В.Т. Бабурин и др.; Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 1994.
4. Статистика рынка товаров и услуг: Учебник / М.К. Беляевский, Г.Д. Кулагина, А.В. Коротков и др.; Под ред. М.К. Беляевского. – М.: Финансы и статистика,1995.
5. Статистический словарь / Гл. ред. М.А. Королев. – 2-е изд., перераб. и доп. – М.: Финансы и статистика,1989.
6. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа: Руководство для экономистов / Пер.с нем. и предисл. Б.М. Ивановой. – М.: Финансы и статистика, 1983.
Приложение
Макеты таблиц для представления результатов группировки
Группировка станков по возрасту
| № |
Возраст оборудования, лет |
Число станков в группе |
Средние по группе эксплуатационные расходы,
тыс. руб.
|
| 1 |
| 2 |
| 3 |
| 4 |
Средние эксплуатационные расходы, тыс. руб.
| Возраст оборудования, лет |
Таблица 1 |
Таблица 2 |
Таблица 3 |
Таблица 4 |
| 1–5 |
| 6–10 |
| 11–15 |
| 16–20 |
| В среднем по всему оборудованию |
1.4 Виды таможенных пошлин
1.4.1 Ввозная и вывозная таможенные пошлины
В зависимости от обложения таможенной пошлиной ввозимых либо вывозимых товаров существует два вида таможенных пошлин:
- ввозная (импортная) таможенная пошлина;
- вывозная (экспортная) таможенная пошлина.
Наибольший перечень товаров (по видам) подлежит обложению ввозными таможенными пошлинами.
Вывозными таможенными пошлинами облагаются в основном товары, отнесенные к категории сырьевых, например, древесина и изделия из нее, древесный уголь, нефть сырая, нефтепродукты, спирт этиловый неденатурированный.
Правовые основы применения в РФ таможенных пошлин закреплены в Законе РФ «О таможенном тарифе». Порядок уплаты таможенной пошлины устанавливается ТК РФ.
Повышая пошлины на импорт, государство создает предпосылки для роста цен на иностранные товары. Таким образом, снижается их конкурентоспособность.
Повышая пошлины на экспорт, государство сдерживает нежелательный вывоз из страны определенных товаров.
В зависимости от обложения таможенной пошлиной ввозимых либо вывозимых товаров она может быть поделена соответственно на два вида: ввозную и вывозную. Причем в отношении вывозной пошлины законодательство может быть подвержено довольно быстрым изменениям [Правовые основания таких изменений закреплены в п. 3 ст. 3 Закона РФ «О таможенном тарифе», где отмечается, что ставки вывозных таможенных пошлин и перечень товаров, в отношении которых они применяются, а также нетарифные меры внешнеэкономического регулирования устанавливаются Правительством Российской Федерации и являются исключительно мерами регулирования внешнеэкономической деятельности на территории Российской Федерации.], в зависимости от складывающейся экономической ситуации в стране.
Можно привести в подтверждение этих слов несколько примеров. Так, достаточно лаконичный историко-правовой анализ введения и отмены экспортной (вывозной) пошлины приводится Козыриным А.Н., в частности, отмечается, что «экспортные пошлины, взимаемые с товаров и транспортных средств при их вывозе за границу, также крайне редко используются в современной мировой торговой практике. В постановлении Верховного Совета РФ от 21 мая 1993 г. «О введении в действие Закона РФ «О таможенном тарифе»» (п. 3) предполагалось ограничить срок применения в Российской Федерации вывозных пошлин до 1 января 1996 г. Однако с наступлением этого срока экспортные пошлины продолжали взиматься. На них приходилось больше половины поступлений таможенных платежей. Принятым в конце 1995 г. Федеральным законом «О государственном регулировании внешнеторговой деятельности» экспортная пошлина была «восстановлена в правах» (ст. 14):
«В целях регулирования операций по импорту и экспорту, в том числе для защиты внутреннего рынка Российской Федерации… в соответствии с федеральными законами и международными договорами Российской Федерации устанавливаются импортные и экспортные пошлины». Но уже 1 апреля 1996 г. было принято постановление Правительства РФ №479 «Об отмене вывозных таможенных пошлин», в котором предусматривалась отмена с I апреля 1996 г. ввозных таможенных пошлин на все товары, за исключением нефти и газового конденсата, а с 1 июля 1996 г. предусматривалось производить экспорт нефти и газового конденсата также без взимания вывозной таможенной пошлины. Во исполнение постановления Правительства РФ был издан Приказ ГТК России от 30 апреля 1996 г. №261 «О ставках вывозных таможенных пошлин», в котором подтверждено прекращение взимания с 1 июля 1996 г. Экспортных пошлин в отношении всех товаров, ввозимых с таможенной территории Российской Федерации». [13]
Однако в настоящее время представленная «биография» экспортной пошлины требует своего продолжения, по причине принятия Правительством РФ постановления от 4 января 1999 г. №17 «Об утверждении ставок вывозных таможенных пошлин на товары, вывозимые с территории Российской Федерации» (где в п. 2 отмечается о признании утратившим силу постановления Правительства Российской Федерации от 1 апреля 1996 г. №479 «Об отмене вывозных таможенных пошлин…») и постановления от 11 января 1999 г. №45 «Об утверждении ставок вывозных таможенных пошлин на товары, вывозимые из Российской Федерации за пределы государств-участников СНГ».
Следует также отметить и некоторые особенности этого нововведения. Во-первых, это мера временная, так как экспортные пошлины вводятся на срок до 6 месяцев (с даты официального опубликования приведенных выше постановлений), а, во-вторых, распространяется на более узкий круг товаров (по сравнению с импортной пошлиной), к которым, например, относятся кокс, газ, смолы, ткани, лесоматериалы (главным образом, товары, относящиеся к категории сырьевых). [16].
1.4.2 Минимальные, преференциальные и максимальные таможенные пошлины
В зависимости от страны происхождения товаров таможенные пошлины могут быть минимальными, преференциальными и максимальными.
Минимальными ставками таможенных пошлин облагаются товары, происходящие из государств, которым при торговле в России предоставлен режим наибольшего благоприятствования. Ставки таможенных пошлин по позициям Товарной номенклатуры внешнеэкономической деятельности Российской Федерации, применяемые к товарам, происходящим из государств, которым Россия предоставляет режим наибольшего благоприятствования, являются базовыми (минимальными). В отношении товаров, происходящих из государств, которым Россия не предоставляет режим наибольшего благоприятствования, или страна происхождения которого не установлена, применяются базовые ставки, увеличенные вдвое (максимальные).
Преференциальные являются разновидностью льготных ставок, предоставляемых отдельным странам или группам стран. В основе определения размера таможенной пошлины заложена таможенная стоимость. Размером таможенной пошлины является сумма, которую необходимо уплатить плательщику по данному платежу. Таможенная стоимость товаров и (или) их количество является налоговой базой для целей исчисления таможенных пошлин. Таможенная стоимость товаров определяется декларантом согласно методам определения таможенной стоимости, установленным Законом РФ «О таможенном тарифе», и заявляется в таможенный орган при декларировании товаров.
Контроль таможенной стоимости осуществляется таможенными органами. Определение таможенной стоимости товаров, ввозимых на таможенную территорию Российской Федерации, производится путем применения следующих методов (статья 18 Закона РФ «О таможенном тарифе»):
* по цене сделки с ввозимыми товарами;
* по цене сделки с идентичными товарами;
* по цене сделки с однородными товарами;
* вычитания стоимости;
* сложения стоимости;
* резервного метода.
Основным методом определения таможенной стоимости является метод по цене сделки с ввозимыми товарами. В том случае, если основной метод не может быть использован, применяется последовательно каждый из перечисленных методов. При этом каждый последующий метод применяется, если таможенная стоимость не может быть определена путем использования предыдущего метода.
Методы вычитания и сложения стоимости могут применяться в любой последовательности.
Тарифные льготы (тарифные преференции) в отношении товаров устанавливаются и не могут носить индивидуального характера. Исключение составляют случаи, предусмотренные статьями 35, 36 и 37 Закона Российской Федерации «О таможенном тарифе». Тарифные льготы предоставляются исключительно по решению Правительства Российской Федерации.
Под тарифной льготой (тарифной преференцией) понимается предоставляемая на условиях взаимности или в одностороннем порядке при реализации торговой политики Российской Федерации льгота в отношении товара, перемещаемого через таможенную границу Российской Федерации в виде возврата ранее уплаченной пошлины, освобождения от оплаты пошлиной, снижения ставки пошлины, установления тарифных квот на преференциальный ввоз (вывоз) товара. [17]
1.4.3 Сезонные и особые пошлины
Следует уделить внимание пошлинам, которые по своей природе, безусловно, являются таможенными, поскольку взимаются таможенными органами при перемещении товаров через таможенную границу РФ, однако в буквальном смысле таковыми рассматриваться не могут.
К таким пошлинам в соответствии с разделом II Закона «О таможенном тарифе» относятся сезонные и особые пошлины. Дело в том, что согласно п. 5 ст. 5 Закона «О таможенном тарифе» пошлина - таможенная пошлина, а также иные виды пошлин, предусмотренные настоящим законом. Эти иные виды пошлин и называются сезонными и особыми пошлинами. Более того, при установлении, например, сезонных пошлин, ставки таможенных пошлин, предусмотренные таможенным тарифом, не применяются (ст. 6 Закона «О таможенном тарифе»). Максимальный срок действия сезонных пошлин составляет шесть месяцев. Как отмечает Козырин А.Н.: «Сезонные пошлины применяются в отношении сельскохозяйственных продуктов и других товаров. Они связаны с так называемыми сезонными ценами, под которыми понимаются закупочные и розничные цены на некоторую продукцию сельского хозяйства (овощи, фрукты, картофель), циклически меняющиеся по временам года.
[Приказ ГТК России от 30 апреля 1998 г. №1998 «О внесении дополнений и изменений в перечень товаров, помещение которых под таможенный режим таможенного склада не допускается».]
Эффективная защита интересов отечественных потребителей и товаропроизводителей от неблагоприятных воздействий мирового рынка предполагает немедленное реагирование таможенного законодательства на существенные сезонные колебания цен на сельскохозяйственные и иные товары». То есть в конечном итоге увеличение стоимости импортируемых сельхозпродукции и иных товаров посредством введения сезонных пошлин, что предполагает создание более благоприятных условий для реализации подобного рода отечественных товаров на внутреннем рынке России.
Особые виды пошлины вводятся в целях защиты экономических интересов Российской Федерации и подразделяются на:
- специальные пошлины;
- антидемпинговые пошлины;
- компенсационные пошлины.
Специальные пошлины могут вводиться как по причинам экономического характера, так и по политическим соображениям. В первом случае специальные пошлины используются как защитная мера, если товары ввозятся на территорию РФ в количествах и на условиях, наносящих или угрожающих нанести ущерб отечественным производителям конкурирующих товаров. Во втором случае специальная пошлина используется в качестве ответной меры на дискриминационные действия в отношении ввоза российских товаров в какую-либо страну. Назначение антидемпинговых пошлин раскрывается в ст. 9 Закона «О таможенном тарифе» и, как отмечается в литературе, связано с наличием трех обстоятельств:
1) фактом ввоза товаров на российскую таможенную территорию по цене более низкой, чем их нормальная цена, сложившаяся на момент ввоза товаров в стране экспорта;
2) наличием материального ущерба или угрозы его нанесения; Содержание и назначение компенсационных пошлин во многом схоже с антидемпинговыми. Разница заключается в том, что компенсационные пошлины применяются в случаях ввоза на территорию РФ товаров, при производстве или вывозе которых прямо или косвенно использовались субсидии (ст. 10 Закона «О таможенном тарифе»).
Как отмечается в ст. 11 Закона «О таможенном тарифе», применению особых видов пошлин (специальных, антидемпинговых, компенсационных) предшествует расследование (проводимое на правительственном уровне). Ставки особых видов пошлин устанавливаются также Правительством РФ по результатам проведенного расследования для каждого отдельного случая, и их размер должен быть соотносим с величиной установленного расследованием демпингового занижения цены, субсидий и выявленного ущерба.
Таким образом, специальная, антидемпинговая, компенсационная пошлины исходят соответственно из количеств и условий ввоза товара, цены ввозимого товара, использования субсидий (облегчающих ввоз товаров). Применяются данные виды пошлин сверх действующих ставок таможенных пошлин. [13]
.2 Понятие таможенной пошлины
Таможенная пошлина - обязательный взнос, взимаемый таможенными органами РФ при ввозе товара на таможенную территорию РФ или вывозе товара с этой территории и являющийся неотъемлемым условием такого ввоза или вывоза (п. 5 ст. 5 Закона РФ «О таможенном тарифе»).
Таможенная пошлина носит характер косвенного налога. Назначение таможенной пошлины двояко, во-первых, Таможенная пошлина может рассматриваться как источник пополнения государственного бюджета, поскольку в соответствии со ст. 19 Закона РФ «Об основах налоговой системы Российской Федерации» отнесена к федеральным налогам а, во-вторых, как способ регулирования ввоза товаров на таможенную территорию РФ и вывоза за ее пределы (с целью защиты российских производителей товаров и обеспечения внутреннего рынка необходимой продукцией). Как совершенно правильно отмечает проф. А.Н. Козырин, таможенно-тарифное регулирование выполняет две основные функции - фискальную и регулятивную.
Фискальная функция состоит во взимании таможенной пошлины и направлении собранных средств в доход федерального бюджета.
Проявления регулятивной функции могут быть самыми разнообразными. Это - рационализация товарной структуры ввоза товаров в Россию; поддержание рационального соотношения вывоза и ввоза товаров, валютных доходов и расходов; изменения в структуре производства и потребления товаров в Российской Федерации; защита экономики России от неблагоприятных воздействий иностранной конкуренции»..
[13]
Сергеев С.П выделяет следующие основные черты таможенной пошлины:
1. Таможенная пошлина - обязательный взнос в федеральный бюджет, который не нарушает при этом конституционной право на свободу предпринимательской деятельности;
2. Таможенная пошлина опосредована процессом перемещения грузов через таможенную границу РФ и является средством достижения данной цели;
3. Таможенная пошлина возмездная, т.е. является платой за предоставление таможенными органами возможности по перемещению грузов через таможенную границу;
4. Таможенная пошлина не обладает регулярностью, так как обязанность ее уплаты возникает лишь при необходимости для субъекта вступить в таможенное правоотношение;
5. Право уплаты таможенной пошлины может быть делегировано иным заинтересованным лицам;
6. Уплата таможенной пошлины обеспечивается принудительной силой государства. [14]
|