2. Структура оптимальных устройств обнаружения.
2.1. Весовой критерий; критерий Неймана-Пирсона.
На практике вместо совместных вероятностей 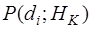 часто пользуются условными вероятностями часто пользуются условными вероятностями
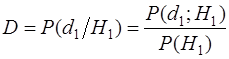 - вероятность правильного обнаружения; - вероятность правильного обнаружения;
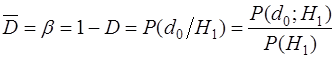 - вероятность пропуска сигнала; - вероятность пропуска сигнала;
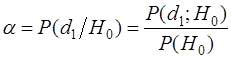 - вероятность ложной тревоги; - вероятность ложной тревоги;
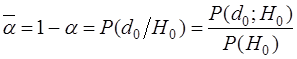 - вероятность правильного необнаружения. - вероятность правильного необнаружения.
Поскольку решения, соответствующие одному и тому же условию являются взаимоисключающими, справедливы равенства
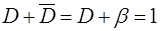 ; ;  . .
Таким образом, можно записать:
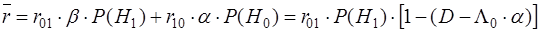
где  - весовой множитель; - весовой множитель;
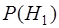 - вероятность наличия полезного сигнала; - вероятность наличия полезного сигнала;
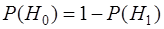 - вероятность его отсутствия. - вероятность его отсутствия.
Очевидно, что при любых 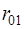 и и 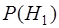 минимум минимум  соответствует максимуму разности соответствует максимуму разности 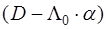 , поэтому критерий минимума среднего риска может быть заменен эквивалентным ему весовым критерием
: , поэтому критерий минимума среднего риска может быть заменен эквивалентным ему весовым критерием
: 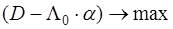 . Оптимизация по этому критерию означает, что при стремлении к максимизации . Оптимизация по этому критерию означает, что при стремлении к максимизации  и минимизации и минимизации  совокупный эффект следует оценивать с весовым множителем совокупный эффект следует оценивать с весовым множителем 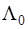 , зависящим от цен ошибок и априорных вероятностей наличия и отсутствия целей. , зависящим от цен ошибок и априорных вероятностей наличия и отсутствия целей.
При сравнении оптимального решающего правило с любым другим справедливо неравенство 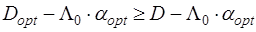 или или 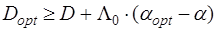 , откуда следует, что при , откуда следует, что при  ; ;  . Это означает, что среди всех правил, для которых вероятность ложной тревоги не больше заданной, оптимальной по весовому критерию обнаружитель обеспечивает максимальную вероятность правильного обнаружения. Существенно, что поскольку весовой коэффициент . Это означает, что среди всех правил, для которых вероятность ложной тревоги не больше заданной, оптимальной по весовому критерию обнаружитель обеспечивает максимальную вероятность правильного обнаружения. Существенно, что поскольку весовой коэффициент 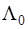 по определению положителен, вышеуказанное неравенство справедливо при любых значениях априорных вероятностей и стоимостей ошибок. по определению положителен, вышеуказанное неравенство справедливо при любых значениях априорных вероятностей и стоимостей ошибок.
Описанный весовой критерий, являющийся видоизменением байесовского, но не требующий знания априорных вероятностей наличия и отсутствия сигнала и стоимости ошибок, широко используется при анализе и синтезе систем обнаружения и носит название критерия Неймана-Пирсона. Решающее правило, оптимальное по этому критерию, соответственно именуют правилом Неймана-Пирсона.
Наряду с критерием Неймана-Пирсона находит применение ряд других критериев.
При неизвестных априорных вероятностях
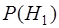 и
и
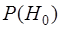 часто за оптимальное принимают решающее правило, обеспечивающее минимум из двух значений условного риска, соответствующих состояниям
часто за оптимальное принимают решающее правило, обеспечивающее минимум из двух значений условного риска, соответствующих состояниям
 и
и
 : :
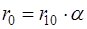 или
или
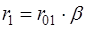 (минимаксный критерий).
(минимаксный критерий).
При известных
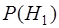 и
и
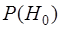 , но невозможности обосновать стоимости ошибочных решений пользуются критерием максимума апостериорной вероятности, т.е. отдают предпочтение гипотезе, апостериорная вероятность которой выше.
, но невозможности обосновать стоимости ошибочных решений пользуются критерием максимума апостериорной вероятности, т.е. отдают предпочтение гипотезе, апостериорная вероятность которой выше.
Если неизвестны и стоимости ошибок и априорные вероятности, применяют критерий максимального правдоподобия; в соответствии с этим критерием выбирается гипотеза, для которой больше условная вероятность функция правдоподобия наблюдавшейся выборки
 или
или
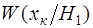 .
.
Важно подчеркнуть, что перечисленные критерии не противоречат, а дополняют друг друга, более того, во многих практически важных случаях оптимизация по любому из этих критериев приводит к одной и той же структуре решающего правила.
2.2. Структура оптимального решающего правила.
Рассмотрим структуру правила, оптимального по весовому критерию ( под структурой решающего правила понимается последовательность математических и логических операций , которые необходимо выполнить над выборочными значениями  , чтобы вынести требуемое решение). , чтобы вынести требуемое решение).
В соответствии с весовым критерием мы должны найти правило, обеспечивающее выполнение условия 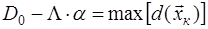 ,где ,где 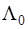 - весовой множитель. - весовой множитель.
Запишем вероятности  и и  в виде в виде
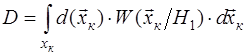 ; ; 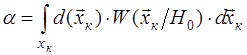 . .
Здесь 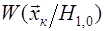 - многомерные плотности вероятности (функции правдоподобия) выборки - многомерные плотности вероятности (функции правдоподобия) выборки  при наличии и отсутствии сигнала (обратите внимание на различие в обозначениях дифференциала при наличии и отсутствии сигнала (обратите внимание на различие в обозначениях дифференциала 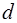 и решающего правила и решающего правила 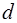 ). ).
Весовой критерий при этом может быть представлен в виде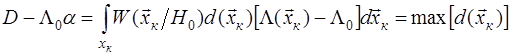 , где , где 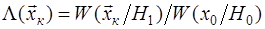 - отношение правдоподобия выборки - отношение правдоподобия выборки  .Чтобы выполнить условие максимума интеграла, достаточно за счет соответствующего выбора решающей функции .Чтобы выполнить условие максимума интеграла, достаточно за счет соответствующего выбора решающей функции 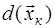 добиться для каждого из возможных значений добиться для каждого из возможных значений 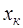 наибольшего значения подынтегральное выражения. Эта функция в нашем случае принимает только два значения: 0 и 1, так что подынтегральное выражение либо обращается в нуль, либо умножается на единицу. Следовательно, максимум интеграла достигается, если для положительных значений подынтегрального выражения принимать наибольшего значения подынтегральное выражения. Эта функция в нашем случае принимает только два значения: 0 и 1, так что подынтегральное выражение либо обращается в нуль, либо умножается на единицу. Следовательно, максимум интеграла достигается, если для положительных значений подынтегрального выражения принимать 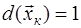 , а для отрицательных , а для отрицательных 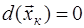 - т.е. - т.е.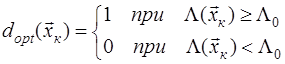
Таким образом, оптимальный в смысле весового критерия обнаружитель представляет устройство вычисления отношения правдоподобия наблюдаемой выборки и сравнения его с фиксированным порогом 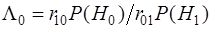 . .
Отношение правдоподобияя, т.е. отношение функций правдоподобия 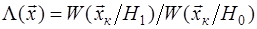 , показывающее, какую из двух взаимоисключающих гипотез (ситуаций) - , показывающее, какую из двух взаимоисключающих гипотез (ситуаций) -  или или  следует считать более вероятной, играет фундаментальную роль втеории различения статистических гипотез, поскольку представляет важнейший случай решающей статистики
. следует считать более вероятной, играет фундаментальную роль втеории различения статистических гипотез, поскольку представляет важнейший случай решающей статистики
.
Решающей статистикой (не путать со статистикой, как областью математической и экономической наук) называют функцию выборочных значений, размерность которой меньше, чем у исходной выборки. Очевидно, что чем меньше размерность решающей статистики, тем проще ее использовать для построения решающего правила. Наилучшей с этой точки зрения является одномерная статистика, например, выборочное среднее 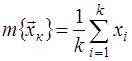 или выборочные моменты более высоких порядков. Однако сокращение размерности (редукция) выборочных данных не должно приводить к потере содержащейся в выборке полезной информации, на основании которой решается задача различения статистических гипотез. Статистика, обладающая таким свойством, называется достаточной
; среди достаточных статистик наибольший интерес представляет минимальная
достаточная статистика, т.е. статистика минимальной размерности, при которой свойство достаточности еще сохраняется. Доказано, что в том случае, когда элементы выборки или выборочные моменты более высоких порядков. Однако сокращение размерности (редукция) выборочных данных не должно приводить к потере содержащейся в выборке полезной информации, на основании которой решается задача различения статистических гипотез. Статистика, обладающая таким свойством, называется достаточной
; среди достаточных статистик наибольший интерес представляет минимальная
достаточная статистика, т.е. статистика минимальной размерности, при которой свойство достаточности еще сохраняется. Доказано, что в том случае, когда элементы выборки 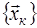 как при гипотезе, так и при альтернативе статически независимы, отношение правдоподобия является минимальной достаточной статистикой при различении простых гипотез. (Напомним, что необходимым и достаточным условием независимости выборочных значений является факторизация функций правдоподобия, т.е. возможность их представления в виде как при гипотезе, так и при альтернативе статически независимы, отношение правдоподобия является минимальной достаточной статистикой при различении простых гипотез. (Напомним, что необходимым и достаточным условием независимости выборочных значений является факторизация функций правдоподобия, т.е. возможность их представления в виде 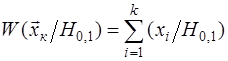 ). ).
В более общем случае это свойство отношения правдоподобия может нарушаться, однако и в этом случае квазиоптимальные алгоритмы часто используют статистику отношения правдоподобия.
Можно также показать, что в случае различения простых гипотез полученная структура обнаружителя – “вычислитель отношения правдоподобия + постоянный порог” - является оптимальной не только весового критерия, но и для других, рассмотренных нами: Неймана-Пирсона, максимума апостериорной вероятности, максимального правдоподобия, минимаксного. Различие этих критериев выражается только в величине порога . .
Очевидно, что для рассмотренной структуры решающего правила его оптимальность не нарушится, если отношение правдоподобия заменить любой монотонной однозначной функцией от него (при условии соответствующего пересчета значения решающего порога). Часто в качестве такой функции используют логарифм отношения правдоподобия 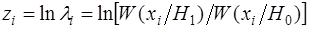 . Переход к этой статистике удобен при независимых
выборках, когда функции правдоподобия факторизуется. При этом . Переход к этой статистике удобен при независимых
выборках, когда функции правдоподобия факторизуется. При этом 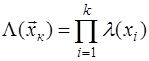 , соответственно , соответственно 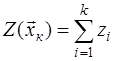 , т.е. при вычислении решающей статистики операция умножения заменяется существенно более простой операцией суммирования. , т.е. при вычислении решающей статистики операция умножения заменяется существенно более простой операцией суммирования.
Самостоятельную роль в теории принятия статистических решений играет математическое ожидание логарифма отношения правдоподобия 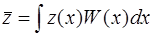 (информация Кульбака-Леблера
). Величина (информация Кульбака-Леблера
). Величина  может служить количественной мерой статистического “расстояния” между различаемыми распределениями. Смысл этой величины достаточно нагляден: чем больше площадь перекрытия одномерных функций правдоподобия может служить количественной мерой статистического “расстояния” между различаемыми распределениями. Смысл этой величины достаточно нагляден: чем больше площадь перекрытия одномерных функций правдоподобия 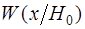 и и 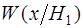 , тем ближе к нулю (в среднем) логарифм отношения правдоподобия и наоборот, чем меньше площадь перекрытия кривых , тем ближе к нулю (в среднем) логарифм отношения правдоподобия и наоборот, чем меньше площадь перекрытия кривых 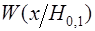 , тем большую модуль информация Кульбака-Леблера. Величина , тем большую модуль информация Кульбака-Леблера. Величина  может интерпретироваться как среднее приращение
статистики может интерпретироваться как среднее приращение
статистики  на один элемент выборки (шаг наблюдения) в процессе ее накопления, поэтому средний объем выборки, необходимый для вынесения решения с заданными вероятностями ошибок a
и b
, обратно пропорционален этой величине (подробнее см. следующие разделы). на один элемент выборки (шаг наблюдения) в процессе ее накопления, поэтому средний объем выборки, необходимый для вынесения решения с заданными вероятностями ошибок a
и b
, обратно пропорционален этой величине (подробнее см. следующие разделы).
Необходимо подчеркнуть. Что операция расчета логарифма отношения правдоподобия может реализовываться с помощью устройств согласованной фильтрации (известно, что выходной эффект фильтра, согласованного с наблюдаемой выборкой, пропорционален логарифму отношения правдоподобия этой выборки). На практике оптимальная обработка выборки обычно разделяется на два этапа: согласованную фильтрацию одиночного
сигнала
и расчет отношения правдоподобия для последовательности
отсчетов
, наблюдаемых на выходе согласованного фильтра. Поэтому мы под формированием решающей статистики будем понимать расчет отношения правдоподобия (или его логарифма) для выборки, наблюдаемой на
выходе
фильтра
(коррелятора) согласованного
с одиночным сигналом.
2.3. Расчет отношения правдоподобия для простых гипотез.
Проведем расчет отношения правдоподобия при простых гипотезах, когда соответствующие функции правдоподобия 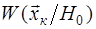 ; ; 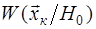 не содержат неизвестных параметров. Рассмотрим случай обнаружения сигнала с известной амплитудой не содержат неизвестных параметров. Рассмотрим случай обнаружения сигнала с известной амплитудой  и начальной фазой и начальной фазой  . (Для радиолокации этот случай является идеализированным, т.к. соответствует обнаружению цели с известной ЭПР, находящейся на известной дальности и обладающей известной радиальной скоростью. Однако такая модель сигнала наиболее наглядна, а также служит исходной для других, более сложных моделей, рассматриваемых ниже.) . (Для радиолокации этот случай является идеализированным, т.к. соответствует обнаружению цели с известной ЭПР, находящейся на известной дальности и обладающей известной радиальной скоростью. Однако такая модель сигнала наиболее наглядна, а также служит исходной для других, более сложных моделей, рассматриваемых ниже.)
В качестве помехи, присутствующей на выходе оптимального приемника будем рассматривать узкополосный гауссовский шум, среднеквадратическое отклонение которого s
также считается известным. Для удобства будем рассматривать амплитуды принятого и расчетного сигналов, нормированные относительно с.к.о. шума: 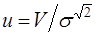 ; ; 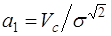 . .
Известно, что оптимальный фильтр такого сигнала представляет собой коррелятор, на опорный вход которого подается полная (с точностью до начальной фазы  ) копия ожидаемого сигнала. Напряжение на выходе коррелятора описывается совокупностью отсчетов его огибающей ) копия ожидаемого сигнала. Напряжение на выходе коррелятора описывается совокупностью отсчетов его огибающей и фазы и фазы  относительно опорного гармонического колебания, синфазного с сигналом. относительно опорного гармонического колебания, синфазного с сигналом.
Соответствующие гипотезам  и и  совместные плотности распределения отсчетов огибающей и фазы для выборки, содержащей совместные плотности распределения отсчетов огибающей и фазы для выборки, содержащей  пар отсчетов, можно записать в виде: пар отсчетов, можно записать в виде:
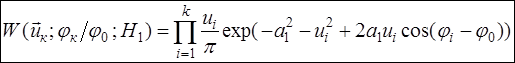 (2.1) (2.1)
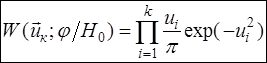 (2.2). (2.2).
Соответственно, отношение правдоподобия и его логарифм
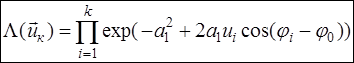 , , 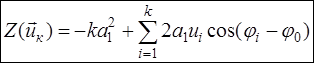 . .
Последнее выражение определяет функциональное преобразование, которому должны подвергаться отсчеты амплитуды и фазы на выходе согласованного фильтра при расчете логарифма отношения правдоподобия выборки ( ). ).
На практике для удобства в качестве выходного эффекта оптимального фильтра обычно рассматривают напряжение на выходе амплитудно-фазового
детектора
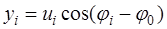 . .
Очевидно, что в этом случае 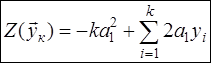 . (3.3) . (3.3)
Рассчитаем математическое ожидание статистики (2.3), т.е. ее среднее приращение (информацию Кульбака-Леблера), приходящееся на один отсчет  . .
Используя известную формулу плотности вероятности произведения двух случайных величин, нетрудно убедиться, что при наличии сигнала величина  имеет нормальное распределение: имеет нормальное распределение:
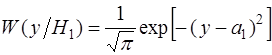 (2.4) (2.4)
мат. ожидание которого 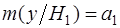 , а дисперсия , а дисперсия  . При нулевой гипотезе ( . При нулевой гипотезе (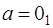 ) мат.ожидание ) мат.ожидание 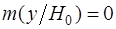 , дисперсия не меняется. Поскольку преобразование (2.3) линейно относительно , дисперсия не меняется. Поскольку преобразование (2.3) линейно относительно  можно утверждать, что распределение решающей статистики можно утверждать, что распределение решающей статистики 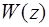 также нормально с параметрами: также нормально с параметрами:
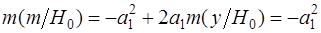 ; ; 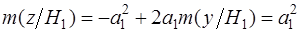 ; ; 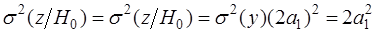 (2.5) (2.5)
Таким образом, для полностью известного сигнала абсолютная величина информации Кульбака-Леблера при гипотезе и альтернативе одинакова и равна квадрату эффективного значения  . .
|