| содержание
Задача 1. 4
Задача 2. 6
Задача 3. 8
Задача 4. 11
Список используемой литературы.. 15
x – количество тысяч деталей, выпускаемых цехами a, b, c i-го склада, где i – номер склада.
xa1 - количество тысяч деталей, выпускаемых цехом a c 1-го склада
xa2 - количество тысяч деталей, выпускаемых цехом a c 2-го склада
xa3 - количество тысяч деталей, выпускаемых цехом a c 3-го склада
xa4 - количество тысяч деталей, выпускаемых цехом a c 4-го склада
xb1 - количество тысяч деталей, выпускаемых цехом b c 1-го склада
xb2 - количество тысяч деталей, выпускаемых цехом b c 2-го склада
xb3 - количество тысяч деталей, выпускаемых цехом b c 3-го склада
xb4 - количество тысяч деталей, выпускаемых цехом b c 4-го склада
xc1 - количество тысяч деталей, выпускаемых цехом c c 1-го склада
xc2 - количество тысяч деталей, выпускаемых цехом c c 2-го склада
xc3 - количество тысяч деталей, выпускаемых цехом c c 3-го склада
xc4 - количество тысяч деталей, выпускаемых цехом c c 4-го склада
Так как производительность цехов в день известна, то можно записать следующее:

Зная пропускную способность складов за день, запишем:
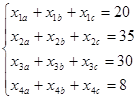
Запишем целевую функцию, при которой стоимость перевозок будет минимальна:
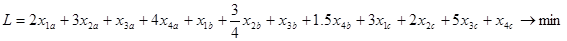
Имеем классическую транспортную задачу с числом базисных переменных, равным n+m–1 , где m–число пунктов отправления, а n – пунктов назначения. В решаемой задаче число базисных переменных равно 4+3-1=6
Число свободных переменных соответственно 12-6=6
Примем переменные x1a, x1b, x2a, x1с, x4с, x3b в качестве базисных, а переменные x2c, x3c, x2b, x3а, x4а, x4b в качестве свободных.
Далее в соответствии с алгоритмом Симплекс метода необходимо выразить базисные переменные через свободные:
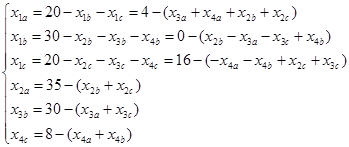
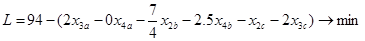
В задании требуется найти минимум функции L. Так как коэффициент при переменной x3a меньше нуля, значит найденное решение не является оптимальным.
Составим Симплекс таблицу:

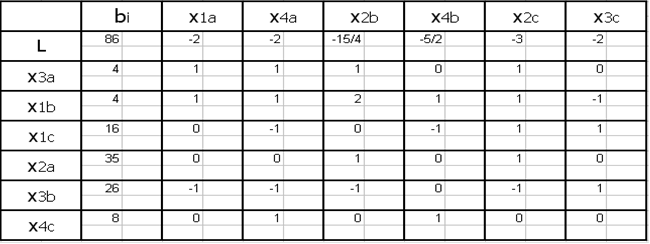
Ответ: при перевозке x3a=4, х1b=4, х1с=16, х2а=35, х3b=26, х4с=8, х1а=х4а=x2b=x4b=x2c=x3c=0 тыс/изд стоимость будет минимальна и составлять 86 тыс/руб.
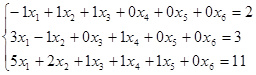
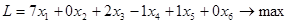
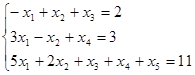
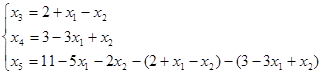


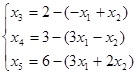
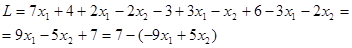

| |
|
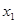
|
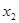
|
| 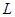
|
7
9
|
-9
3
|
5
-3
|
| 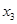
|
2
1
|
-1
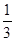
|
2
-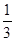
|
| 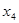
|
3
1
|
3
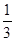
|
-1
-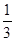
|
| 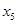
|
6
-3
|
3
-1
|
2
1
|
Так как все 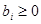 , то это опорное решение. , то это опорное решение.
Найдем оптимальное решение.
Данное решение является оптимальным, так как все коэффициенты при переменных в целевой функции положительные.
Ответ: 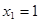 , , 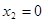 , , 
Заданная задача – транспортная задача с неправильным балансом (избыток заявок).
Необходимо ввести фиктивный пункт отправления Аф с запасом 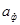 : :
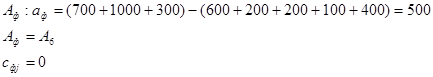
Для нахождения опорного плана используем метод «Северо-западного угла».
| |
В1
|
В2
|
В3
|
|
| А1
|
12
600
|
42
|
25
|
600
|
| А2
|
21
100
|
18
100
|
35
|
200
|
| А3
|
25
|
15
200
|
23
|
200
|
| А4
|
21
|
30
100
|
40
|
100
|
| А5
|
20
|
32
400
|
50
|
400
|
| АФ
|
0
|
0 200
|
0
300
|
500
|
| 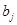
|
700
|
1000
|
300
|
2000
|

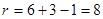

Решение является опорным.
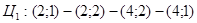

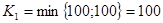
| |
В1
|
В2
|
В3
|
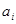
|
| А1
|
12
600
|
42
|
25
|
600
|
| А2
|
21
|
18
200
|
35
|
200
|
| А3
|
25
|
15
200
|
23
|
200
|
| А4
|
21
100
|
30
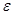
|
40
|
100+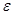
|
| А5
|
20
|
32
400-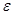
|
50
|
400-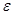
|
| АФ
|
0
|
0 200
|
0
300
|
500
|
| 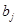
|
700
|
1000
|
300
|
2000
|
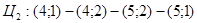
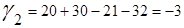
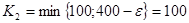
Решение является опорным, но вырожденным. Для того чтобы свести вырожденный случай к обычному решению, изменим запасы на малую положительную величину  так, чтобы общий баланс не нарушился. так, чтобы общий баланс не нарушился.
| |
В1
|
В2
|
В3
|
|
| А1
|
12
600
|
42
|
25
|
600
|
| А2
|
21
|
18
200
|
35
|
200
|
| А3
|
25
|
15
200
|
23
|
200
|
| А4
|
21
|
30
100+
|
40
|
100+
|
| А5
|
20
100
|
32
300-
|
50
|
400-
|
| АФ
|
0
|
0 200
|
0
300
|
500
|
| 
|
700
|
1000
|
300
|
2000
|
Получили оптимальное решение.
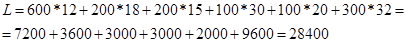
Проверим правильность решения задачи методом потенциалов.
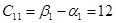 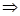 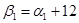
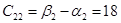 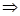 
 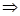 
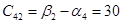 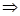 
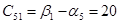 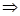 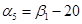
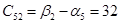 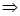 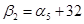
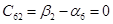 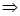 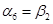
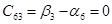 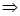 
Пусть 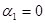 , тогда , тогда 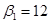
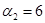
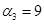

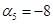
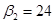
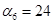
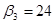
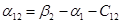  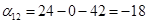  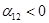
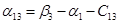  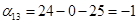  
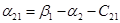    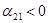
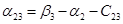  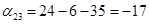  
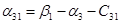  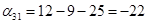  
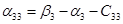    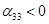
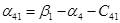  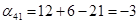  
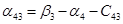  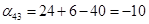  
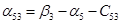  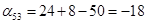  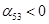
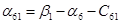  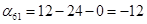  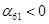
Так как среди найденных чисел 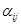 нет положительных, то найденный план является оптимальным. нет положительных, то найденный план является оптимальным.
Ответ: 28400
Найти 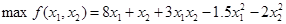
При ограничениях 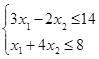  
1) Определение стационарной точки
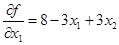

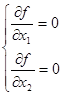  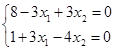  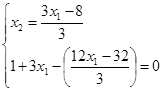 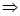  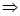   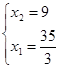
2) Проверка стационарной точки на относительный максимум или минимум
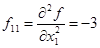 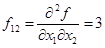
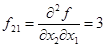 
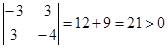 , , 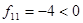 , следовательно, стационарная точка является точкой относительного максимума. , следовательно, стационарная точка является точкой относительного максимума.
3) Составление функции Лагранжа


Применяем к функции Лагранжа теорему Куна-Таккера.

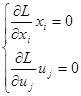
 I I
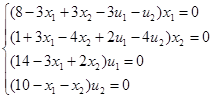 II II
4) Нахождение решение системы I. Оставим все свободные переменные в правой части.
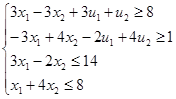
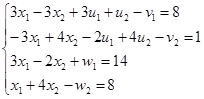 (1) (1)
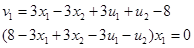
(из II)
Система уравнений II определяется условиями дополняющей нежесткости:
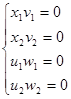
5) Введем искусственные переменные  , , 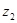 в первые два уравнения системы (1) со знаками, совпадающими со знаками соответствующих свободных членов: в первые два уравнения системы (1) со знаками, совпадающими со знаками соответствующих свободных членов:
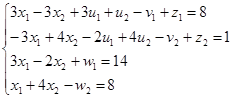
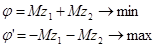
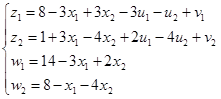

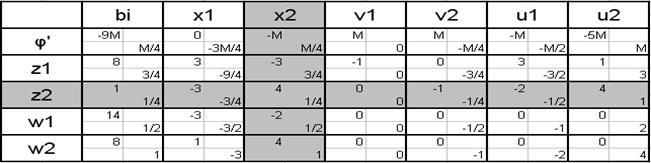 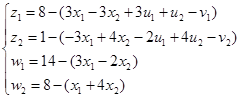
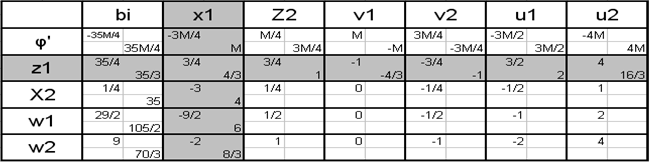 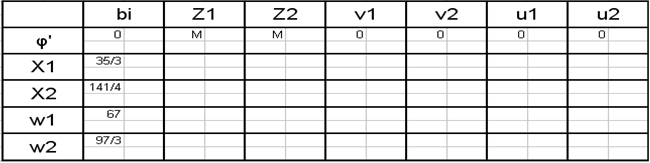
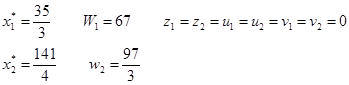
Проверяем условие выполнения дополняющей не жесткости:
 Все четыре условия выполняются Все четыре условия выполняются
Ответ: Решения 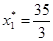 и и  являются оптимальным решением квадратичного программирования. являются оптимальным решением квадратичного программирования.
Тогда 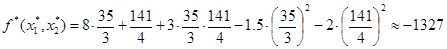
1. Волков И. К., Загоруйко Е. А. Исследование операций. – Москва: Издательство МГТУ имени Баумана Н. Э., 2000г. – 436с.
2. Кремер Н. Ш. Исследование операций в экономике. – Москва: Издательское объединение «ЮНИТИ», 1997г. – 407с.
3. Курс лекций Плотникова Н.В.
|