| Министерство образования Российской Федерации
Кубанский государственный технологический университет
Кафедра …
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по предмету
локальные системы автоматики
тема курсового проекта
:
«Разработка локальной системы управления
промышленным объектом».
Выполнил
: студент гр. ??–??–??
…
номер зачётной книжки ??–??–???
Руководитель
: доц. каф. ??
…
Краснодар
2001
Министерство образования Российской Федерации
Кубанский государственный технологический университет
ЗАДАНИЕ
На курсовой проект …
Студенту группы ??–??–??
По дисциплине Локальные системы автоматики
Тема курсового проекта Разработка локальной системы

управления промышленным объектом

Исходные данные Объект автоматизации – аппарат для
производства фотографической эмульсии. Общая емкость – 700 л,

длительность процесса – 1.2 ч. В ходе процесса необходимо

поддерживать постоянную температуру и избыток ионов Br-
.
1 Выполнить задания:
1.1 Анализ и моделирование объекта управления
 1.2 Обоснование структуры и расчет системы управления 1.2 Обоснование структуры и расчет системы управления
1.3 Выбор технических средств

2 Выполнить графические работы:
2.1 Выполнить лист результатов исследования объекта и системы
2.2 Выполнить схему автоматизации
3 Оформить расчётно-пояснительную записку
4 Основная литература
Основы технологии светочувствительных материалов. Под ред.

проф. Шеберстова. – М.: Химия, 1977. – 504 с.
Задание выдано 27.02.2001
Срок сдачи проекта 17.05.2001
Задание принял
Руководитель …
Проект защищен
С оценкой
ЧЛЕНЫ КОМИССИИ :
РЕФЕРАТ

ЛОКАЛЬНАЯ СИСТЕМА АВТОМАТИКИ, РЕГУЛИРУЕМАЯ ВЕЛИЧИНА, РЕГУЛИРУЮЩЕЕ ВОЗДЕЙСТВИЕ, РЕГУЛЯТОР, КАЧЕСТВО РЕГУЛИРОВАНИЯ, ОПТИМАЛЬНАЯ НАСТРОЙКА, НАДЕЖНОСТЬ СИСТЕМЫ.
Курсовой проект содержит 49 страниц, 28 рисунков, 4 источника.
В данном курсовом проекте рассмотрен вопрос синтеза локальной системы управления установкой для получения фотографической эмульсии. В работе произведен анализ объекта регулирования, построены передаточные функции объекта по каналам управления и возмущения, на основе чего были обоснованы структура и параметры системы управления. Число регулируемых величин у объекта – 2, число контролируемых – 4 (в их число входят и регулируемые величины). Элементы и устройства системы регулирования были выбраны из числа серийно выпускаемых отечественной промышленностью. В работе были также рассчитаны погрешность комплектов, применяемых для измерения регулируемых величин, а также надежность одного из комплектов.

СОДЕРЖАНИЕ
Введение ........................................................................5
1 Функциональный и технико-экономический анализ объекта управления .................................................................6
1.1 Сведения о строении фотопленок ...................................6
1.2 Краткие сведения об аппарате эмульсификации.................7
2 Моделирование объекта управления................................10
2.1 Получение модели по величине pBr
...............................10
2.2 Получение тепловой модели .........................................14
3 Выбор и обоснование регулируемых величин и регулирующих воздействий ...............................................................24
4 Формирование структуры системы управления.................25
5 Расчет элементов и параметров системы..........................28
5.1 Расчет и выбор регулирующего органа для расхода воды....28
5.2 Выбор регулирующего органа для расхода реагентов........30
5.3 Расчет и выбор измерительных преобразователей..............31
5.3.1 Выбор комплекта для измерения pBr
...........................31
5.3.2 Выбор комплекта для измерения температуры...............32
5.4 Выбор и обоснование регуляторов. Расчет настроек. .........34
5.4.1 Расчет регулятора для pBr
........................................35
5.4.2 Расчет регулятора для температуры ..........................39
6 Выбор технических средств ...........................................44
Заключение.....................................................................46
Список литературы ...........................................................47
Приложение А .................................................................48
 ВВЕДЕНИЕ ВВЕДЕНИЕ
В работе рассмотрена часть процесса промышленного производства фотографической эмульсии. Следует отметить, что полный технологический цикл этого производства состоит из большого количества стадий, и рассмотренный в данной работе процесс представляет собой только совмещенные друг с другом первые две стадии: эмульсификация и первое (физическое) созревание. Процессы студенения, измельчения и полива фотографической эмульсии в данной работе не рассматриваются из-за того, что для каждого из них необходима своя локальная система, а для координации работы необходимо использовать систему управления более высокого уровня в иерархии управления.
Установлено, что для получения качественного продукта необходимо поддерживать достаточно жесткий режим для многих технологических параметров процесса. Например, отклонение температурного режима на 20% от номинального может привести не только к значительному ухудшению качества, но и к необратимой порче продукта. Поэтому применение автоматической системы регулирования в данном случае становится просто необходимым.
1  ФУНКЦИОНАЛЬНЫЙ И ТЕХНИКО-ЭКОНОМИЧЕСКИЙ АНАЛИЗ ОБЪЕКТА УПРАВЛЕНИЯ ФУНКЦИОНАЛЬНЫЙ И ТЕХНИКО-ЭКОНОМИЧЕСКИЙ АНАЛИЗ ОБЪЕКТА УПРАВЛЕНИЯ
1.1 Сведения о строении фотопленок
Вначале кратко опишем схему строения фотографического галогеносеребряного светочувствительного материала (см. рисунок 1.1)
Рисунок 1.1 – Строение галогеносеребряной эмульсии
Цифрой 1 обозначен верхний защитный слой
из хорошо задубленной желатины. Фотографическая желатина – это основная коллоидная среда для эмульсий. Она представляет собой сложное вещество белковой природы, получаемое при гидролизе коллагена. Под защитным слоем находится наиболее важная составная часть фотографического материала – светочувствительный
или эмульсионный
слой 2; в нем протекают все процессы, приводящие в конечном результате к образованию фотографического изображения. Эмульсионный слой представляет собой пленку воздушно-сухой желатины, в которой во взвешенном состоянии находятся микрокристаллы галогенида серебра (чаще всего AgBr
с некоторой примесью AgI
или AgCl
), так называемые эмульсионные зерна (эмульсионные кристаллы
); толщина эмульсионного слоя для разных фотоматериалов различна и лежит в диапазоне от 4 до 25-30 мкм.
Эмульсионный слой скреплен с подложкой 5 при помощи подслоя
4 – желатинового слоя с добавками дубителя и веществ, способствующих склеиванию эмульсионного слоя и подложки; толщина подслоя ~ 1 мкм. Подложка
представляет собой гибкую пленку, бумагу или стекло; гибкая пленочная подложка называется обычно основой
. На основу со стороны, обратной эмульсионному слою, иногда бывает нанесен противослой
6, препятствующий скручиванию пленки.
Наиболее важной составной частью фотографического материала являются эмульсионные кристаллы: они поглощают свет, в них образуется скрытое изображение, они в процессе проявления превращаются в зерна серебра, создающие почернение слоя и, следовательно, в конечном результате видимое фотографическое изображение.

1.2 Краткие сведения об аппарате эмульсификации
В процессе получения фотографических галогеносеребряных эмульсий, проводимом в механизированной аппаратуре периодического действия, различают следующие стадии [1, с.61-64]:
1) подготовка и дозирование сырьевых материалов (желатины, нитрата серебра, хлорида натрия, бромида и йодида калия или аммония, водного аммиака, дистиллированной воды) и приготовление растворов этих веществ;
2) эмульсификация;
3) первое, или физическое созревание эмульсии;
4) стадия перехода от первого созревания ко второму;
5) второе, или химическое созревание;
6) завершающая стадия (студенение, измельчение, расфасовка);
7) хранение готовой эмульсии.
Рассмотрим более подробно вторую стадию процесса.
Эмульсификация состоит в образовании твердой фазы галогенидов серебра в результате реакции двойного обмена между нитратом серебра (или аммиакатом серебра при аммиачном способе) и галогенидами щелочных металлов или аммония в присутствии защитного коллоида – желатины:
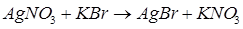
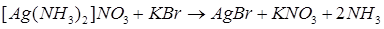
При эмульсификации образуется пересыщенный раствор галогенида серебра, выделяются центры кристаллизации и начинается процесс кристаллизации эмульсионных зерен (эмульсионных микрокристаллов). Условиями образования галогенида серебра определяются конечные свойства фотографической эмульсии.
Опишем наиболее современный из применяющихся на сегодняшний день аппаратов для эмульсификации, построенный по двухструйной схеме (см. рисунок 1.2).
Эмульсификация и первое созревание проводится при непрерывной циркуляции эмульсии из аппарата первого созревания через реакционную камеру смесителя с малой зоной перемешивания и эффективной мешалкой. Смеситель 3 выполняет одновременно роль эмульсификатора и насоса для циркуляции потока. В смеситель из сборников-термостатов 1 дозирующими насосами 2 непрерывно подают растворы нитрата серебра и галогенида щелочного металла. Предварительно в аппарате готовят раствор эмульсификационной
 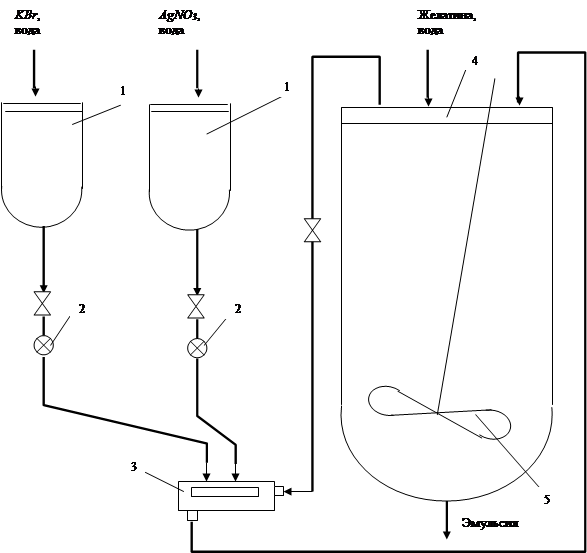
Рисунок 1.2 – Общая схема установки двухструйной эмульсификации
желатины, который с помощью водяной рубашки подогревают до температуры ~ 45 ºC. При включении мешалки смесителя раствор
желатины засасывается из аппарата 4 по трубопроводу и поступает в
смеситель, где смешивается с растворами реагентов; в результате в эмульсификационной среде возникают зародыши микрокристаллов галогенида серебра. В дальнейшем в аппарате 4 образуется фотографическая эмульсия, которая непрерывно циркулирует через зону смешения в смесителе 3 и обогащается новыми образованиями галогенида серебра, одновременно с течением кристаллизационного процесса в потоке, проходящем через накопитель 4 и смеситель 3. Процесс ведут при работающей мешалке 5.
Главными условиями получения качественной эмульсии являются:
– поддержание в реакционной среде избытка ионов галогена;
– поддержание постоянного температурного режима.
Опишем более подробно стадии процесса и приведем численные значения основных характеристик процесса.
1)  введение желатины 2%-раствора в течение 3-5 мин; введение желатины 2%-раствора в течение 3-5 мин;
2) включение циркуляционного насоса. Расход – 10 м3
/ч;
3) нагрев раствора до 45±1 ºC – термостатирование;
4) ввод:
– смачивателя;
– дубителя;
– этанола;
– этиленгликоля.
5) ввод KNO3
10%-раствора 1л за 10 мин до начала процесса;
6) ввод KBr
1N-раствора объемом 0.1 л. Суммарный объем смеси до начала процесса – 0.2 л.
7) ввод NH3
25%-раствора 0.01 л.
8) начало кристаллизации. Показатели процесса: T=45±1 ºC; pBr
=3.3±0.2. Данные параметры – температуру раствора и концентрацию ионов Br
-
– следует поддерживать постоянными в течение всего процесса.
9) Начало ввода растворов 1 и 2 одновременный. В дальнейшем под раствором 1 будем понимать сантинормальный раствор (то есть на 1л приходится 0.01 моль растворенного вещества) KBr
, а под раствором 2 – сантинормальный раствор AgNO3
.
10) ввод растворов вести со скоростью ~140 л/ч, всего нужно подать по 160 л.
11) сигналом окончания процесса служит достижение нижнего уровня в одной из емкостей с раствором 1 или 2.
Необходимо отметить, что оценивать качество получающегося продукта в “реальном времени” невозможно, т.к. довольно трудно представить датчик формы и дисперсности микрокристаллов AgBr
в растворе желатины. Поэтому единственным способом поддерживать должное качество фотографической эмульсии является слежение за основными параметрами процесса эмульсификации – температурой и показателем концентрации ионов галогена pBr
, и поддержание их значений на постоянном (в пределах точности) уровне. Отклонение температуры раствора на 10 ºC в обе стороны от номинала или отклонение величины pBr
на 1 единицу от номинала приводят к порче продукта.
Таким образом, необходимо с максимально возможной точностью поддерживать два заданных технологических параметра на номинальных значениях, не допускать выхода их значений за допустимые пределы и контролировать ряд вспомогательных технологических параметров – температуру воды в рубашке, величину pH исходного раствора.
2  МОДЕЛИРОВАНИЕ ОБЪЕКТА УПРАВЛЕНИЯ МОДЕЛИРОВАНИЕ ОБЪЕКТА УПРАВЛЕНИЯ
Конечной целью моделирования процессов в аппарате эмульсификации (далее просто аппарате) является получение линеаризованных динамических зависимостей между входными и выходными величинами процесса, на основании чего легко построить передаточные функции по соответствующим каналам. Однако надо учесть, что в будущем объект будет включен в схему автоматизации, а это значит, что на его вход будет воздействовать исполнительный механизм (в дальнейшем – ИМ) совместно с регулирующим органом (в дальнейшем – РО), а регулируемая величина будет преобразовываться с помощью датчика, поэтому суммарная передаточная функция будет равна произведению передаточных функций собственно объекта, РО и датчика.
Мы определили, что регулируемыми величинами объекта являются температура и показатель концентрации pBr
в аппарате. Рассмотрим отдельно факторы, влияющие на каждую из величин и построим модели, описывающие изменение выходной величины в зависимости от изменений выбранных входных величин.
2.1 Получение модели по величине pBr
При получении модели будем руководствоваться рисунком 1.2, представляющим собой упрощенную схему технологической установки – на нем не показаны тепловая рубашка и контур циркуляции воды из рубашки.
С учетом того, что KBr
является сильным электролитом, т.е. переходя в раствор, практически полностью распадается на ионы, то величина pBr
перед началом процесса полностью определяется концентрацией KBr
в исходной среде (c1
).
Кроме того, описанная в пункте 1.2 основная реакция:
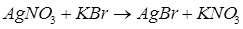
не является обратимой, т.е., идет до конца, поскольку основной конечный продукт AgBr
является чрезвычайно слабо растворимым веществом. Из этого можно сделать вывод, что общая концентрация ионов Br-
в растворе на протяжении всего процесса определяется количеством непрореагиро-
вавшего вещества KBr
.
В аппарате установлена мешалка и, кроме того, присутствует контур рециркуляции. Это дает основание отнести его к идеализированному классу аппаратов идального смешения. А именно, под аппаратом идеального смешения понимают такой аппарат, в котором концетрации интересующего нас вещества во всех точках его реакционного объема равны.
Для построения модели сделаем еще одно допущение – примем скорость реакции как величину, гораздо большую, чем скорость поступления реагентов. Это оправдано, поскольку растворы 1 и 2 поступают в достаточно малый реакционный объем смесителя, в котором создано достаточно сильное перемешивание. Поэтому считаем, что скорость изменения концентрации Br-
в аппарате полностью зависит от скоростей подачи реагентов.
 Пусть V·c
– общее количество вещества KBr
(а следовательно, и количество ионов Br-
) в аппарате в данный момент времени. Запишем уравнение динамики для изменения количества вещества: Пусть V·c
– общее количество вещества KBr
(а следовательно, и количество ионов Br-
) в аппарате в данный момент времени. Запишем уравнение динамики для изменения количества вещества:
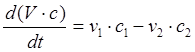 , (2.1) , (2.1)
где v1
, v2
– объемные скорости подачи раствора 1 и 2 соответственно, м3
/с
;
c1
, c2
– мольные концентрации растворов 1 и 2 соответственно, моль/м3
;
V
, c
– соответственно объем аппарата и концентрация ионов Br-
.
Учтем, что и объем, и концентрация являются величинами переменными, тогда:
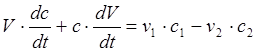 . (2.2) . (2.2)
Запишем уравнение, описывающее изменение объема смеси в аппарате:
 . (2.3) . (2.3)
Система уравнений (2.2) и (2.3) описывает динамику изменения концентрации c
ионов Br-
в аппарате. Поскольку выходной величиной является pBr
, то дополним эту систему уравнением для нахождения pBr
:
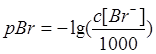 , (2.4) , (2.4)
где c
[Br-
] выражено в моль/м3
.
На основе полученной системы уравнений получим модель динамики аппарата. Следует отметить, что в общем случае она является нелинейной, т.к. коэффициент при 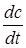 – объем смеси в аппарате – является величиной переменной, зависящей от расходов веществ 1 и 2. Кроме этого, зависимость pBr
от концентрации c
[Br-
] является нелинейной. Существует еще одно обстоятельство, которое не позволяет перейти от уравнений (2.2)–(2.4) к линейным уравнениям в приращениях по известной методике. Дело в том, что для получения уравнения в приращениях необходимо из уравнения динамики вычесть уравнение статики объекта. Под статикой подразумевается такой режим работы объекта, который характеризуется постоянством во времени всех величин, характеризующих его состояние. В нашем объекте при ненулевых расходах растворов 1 и 2 статический режим отсутствует, т.к. объем смеси в аппарате постояно растет. Поэтому если даже предположить, что общее количество ионов Br-
в аппарате постоянно, т.е. правая часть (2.1) равна нулю, концентрация c
[Br-
] будет падать, потому что объем раствора в аппарате будет расти. – объем смеси в аппарате – является величиной переменной, зависящей от расходов веществ 1 и 2. Кроме этого, зависимость pBr
от концентрации c
[Br-
] является нелинейной. Существует еще одно обстоятельство, которое не позволяет перейти от уравнений (2.2)–(2.4) к линейным уравнениям в приращениях по известной методике. Дело в том, что для получения уравнения в приращениях необходимо из уравнения динамики вычесть уравнение статики объекта. Под статикой подразумевается такой режим работы объекта, который характеризуется постоянством во времени всех величин, характеризующих его состояние. В нашем объекте при ненулевых расходах растворов 1 и 2 статический режим отсутствует, т.к. объем смеси в аппарате постояно растет. Поэтому если даже предположить, что общее количество ионов Br-
в аппарате постоянно, т.е. правая часть (2.1) равна нулю, концентрация c
[Br-
] будет падать, потому что объем раствора в аппарате будет расти.
 Все перечисленные соображения позволяют отнести наш аппарат к классу нестационарных химических реакторов. А именно, наш аппарат является реактором идеального смешения полунепрерывного действия [2, с. 54]. Все перечисленные соображения позволяют отнести наш аппарат к классу нестационарных химических реакторов. А именно, наш аппарат является реактором идеального смешения полунепрерывного действия [2, с. 54].
Для получения динамической характеристики аппарата используем пакет Simulink 2.2
, входящий в русифицированную версию Matlab 5.2.1
. На рисунке 2.1 показана схема модели.
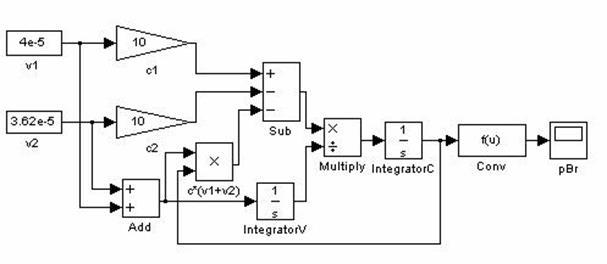
Рисунок 2.1 – Модель объекта по концентрации ионов Br-
В модели все величины для удобства указаны в системе СИ. Начальные условия по объему и концентрации установлены в соответствии с пунктом 1.2. При одинаковых концентрациях растворов 1 и 2, равных номинальным, и при указанных на рисунке расходах получаем следующую кривую pBr
:
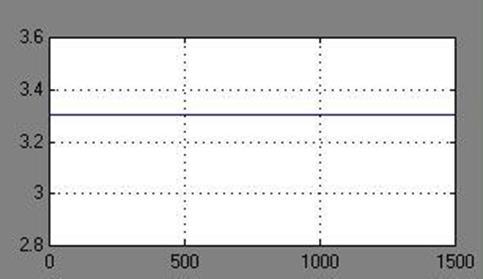
Рисунок 2.2 – Режим поддержания pBr
на постоянном уровне

Видим, что для поддержания постоянного значения pBr
необходимо раствор 1 подавать в избытке.
Регулирование скорости подачи реагентов осуществляется с помощью насоса, приводимого в движение двигателем постоянного тока независимого возбуждения, управляемого тиристорным электроприводом типа ЭТУ, поэтому регулирование скорости вращения вала двигателя и, следовательно, расхода реагентов возможно максимум на 50% меньше максимального значения, поэтому примем, что максимальное отклонение равно 50% от 3.62·10-5
.
Примем, что максимальное отклонение величины pBr
от номинала равно 0.2. Получим переходную характеристику:
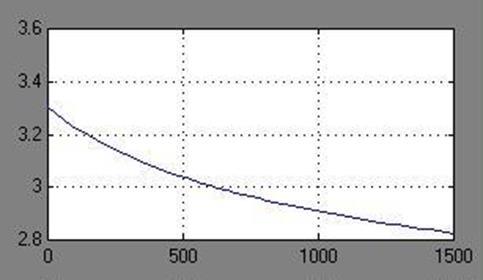
Рисунок 2.3 – Переходный процесс по pBr
Видим, что переходная характеристика не может быть рассмотрена как характеристика апериодического звена, т.к с течением времени она не приходит к установившемуся режиму. В этом случае остается принять линеаризованное описание данного звена как интегрирующего, т.к. интегрирующее – это единственное линейное нестационарное звено, применяющееся в инженерной практике. Наш выбор становится обоснованным еще и потому, что модель строится на весьма ограниченном участке изменения выходной переменной – это следует из ограничений технологии.
Поэтому окончательно принимаем интегрирующий характер объекта по каналу расход вещества 2 – величина pBr
. Выходная величина отклоняется от номинального значения на 0.2 за время 340 с. Поэтому постоянная времени интегрирования равна 340 с ≈ 5.6 мин. Передаточная функция:
 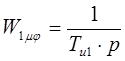 . (2.5) . (2.5)
Дадим возмущение по каналу концентрации одного из реагентов. Предположим, что концентрация раствора 1 выросла с 0.01-нормального до 0.015-нормального. В этом случае получаем переходный процесс, полностью аналогичный изображенному на рисунке 2.3. Однако смоделированное нами возмущение слишком велико, оно составляет 50% от номинального значения. В действительности максимальное отклонение может составлять не более 10%, т.е., в 5 раз меньше. Поэтому примем постоянную интегрирования для канала возмущения в 5 раз меньшую, чем для канала управляющего воздействия, т.е. максимальное отклонение от номинала достигается в 5 раз быстрее. Tи2
= 1.12 мин. Передаточная функция по каналу возмущение концентрации – величина pBr
:
 . (2.6) . (2.6)
2.2 Получение тепловой модели
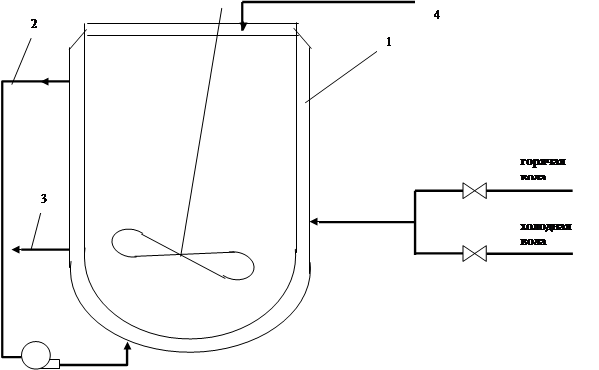 Для нормального протекания процесса эмульсификации необходимо поддерживать температуру раствора в аппарате постоянной. Это достигается использованием тепловой рубашки, внутри которой создается постоянное перемешивание теплоносителя. При необходимости нагрева или охлаждения смеси в аппарате в рубашку подается некоторое количество горячей или холодной воды из соответствующих трубопроводов. Описанная схема теплового взаимодействия показана на рисунке 2.4. Для нормального протекания процесса эмульсификации необходимо поддерживать температуру раствора в аппарате постоянной. Это достигается использованием тепловой рубашки, внутри которой создается постоянное перемешивание теплоносителя. При необходимости нагрева или охлаждения смеси в аппарате в рубашку подается некоторое количество горячей или холодной воды из соответствующих трубопроводов. Описанная схема теплового взаимодействия показана на рисунке 2.4.
Рисунок 2.4 – Тепловая схема процесса
 На рисунке 2.4 цифрами обозначены: 1 – тепловая рубашка (далее – просто рубашка), 2 – контур циркуляции, 3 – сбросная линия, 4 – линия поступления реагентов. На рисунке 2.4 цифрами обозначены: 1 – тепловая рубашка (далее – просто рубашка), 2 – контур циркуляции, 3 – сбросная линия, 4 – линия поступления реагентов.
Циркуляционная линия с насосом введена для того, чтобы избежать образования застойных зон в рубашке, т.к. при отсутствии подачи горячей или холодной воды их образование неминуемо.
При составлении уравнений теплового баланса для рубашки и для аппарата пренебрегаем потерями теплоты в окружающую среду. Кроме того, считаем, что температура во всем объеме рубашки и аппарата постоянна. Это правомерно, поскольку в обоих случаях присутствует интенсивное перемешивание. Таким образом, мы имеем систему двух емкостей – аппарата и рубашки, каждую из которых можно считать аппаратом идеального смешения относительно температуры.
Запишем уравнение динамики для аппарата:
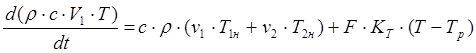 . (2.7) . (2.7)
В левой части уравнения записано изменение количества теплоты в реакторе. Первое слагаемое правой части соответствует приходу теплоты с потоком реагентов, второе слагаемое соответствует притоку теплоты за счет теплообмена с рубашкой.
В этом уравнении применены следующие обозначения:
ρ
– плотность среды в реакторе, кг/м3
;
c
– теплоемкость среды в реакторе, Дж/(кг·К)
;
V1
– объем реакционной смеси, м3
;
T
, T
н
1
, T
н
2
– соответственно текущая температура реакционной смеси и температуры поступающих реагентов, °С
;
v1
, v2
– объемные скорости подачи раствора 1 и 2 соответственно, м3
/с
;
F
– площадь соприкосновения раствора и стенки реактора, м2
;
KТ
– коэффициент теплопередачи от раствора в реакторе к воде в рубашке, Вт/(м2
·
K)
;
(T – T
р
) – разность температур в реакторе и в рубашке °С
.
Знак “+” перед вторым слагаемым мы поставили в предположении, что тепловой поток направлен от рубашки к реактор. В обратном случае этот знак изменится на противоположный.
Запишем уравнение динамики для рубашки:
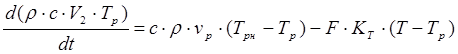 (2.8) (2.8)
В левой части уравнения записано изменение количества теплоты в рубашке. Первое слагаемое правой части соответствует изменению количества теплоты в рубашке за счет притока воды с температурой T
и оттока воды с температурой, равной температуре в рубашке; второе слагаемое соответствует оттоку теплоты за счет теплообмена с реактором.
 В этом уравнении применены следующие обозначения: В этом уравнении применены следующие обозначения:
ρ
– плотность воды в рубашке, кг/м3
;
c
– теплоемкость воды, Дж/(кг·К)
;
V2
– объем рубашки, м3
;
Tр
, T
рн
– соответственно текущая температура в рубашке и температура поступающей из сети воды, °С
;
vр
– объемная скорость подачи воды в рубашку, м3
/с
;
F
– площадь соприкосновения раствора и стенки реактора, м2
;
KТ
– коэффициент теплопередачи от воды в рубашке к раствору в реакторе, Вт/(м2
·
K)
;
(T – T
р
) – разность температур в реакторе и в рубашке °С
.
Дополним полученную систему уравнением для изменения объема реакционной смеси:
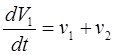 (2.9) (2.9)
Чтобы упростить моделирование, примем теплоемкость смеси в реакторе приблизительно равной теплоемкости воды. Строго говоря, теплоемкость в данном процессе зависит от концентрации желатины и исходных веществ в растворе и является величиной переменной. Однако концентрация исходного раствора желатины невелика, и в дальнейшем при добавлении новых порций реагентов она изменяется незначительно.
Преобразуем (2.7) и (2.8), учитывая, что объем смеси в реакторе является величиной переменной, а объем рубашки – величина постоянная: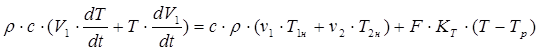 ,(2.10) ,(2.10)
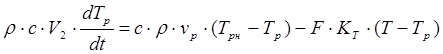 . (2.11) . (2.11)
Совокупность уравнений (2.9) – (2.11) представляет собой математическую модель динамики объекта, в которой выходной величиной служит температура в реакторе, а входными – температуры и расходы входящих потоков реагентов, температура и расход теплоносителя на входе в рубашку.
Следует отметить, что, как и в случае модели, описанной в пункте (2.1), данная модель не является линейной. В дифференциальном уравнении (2.10) многие коэффициенты перед переменными не являются величинами постоянными, а, в свою очередь, зависят от других параметров системы и от начальных условий.
Для получения переходных характеристик температурного режима и последующей линеаризации используем пакет Simulink
. На рисунке 2.5 показана схема модели.
 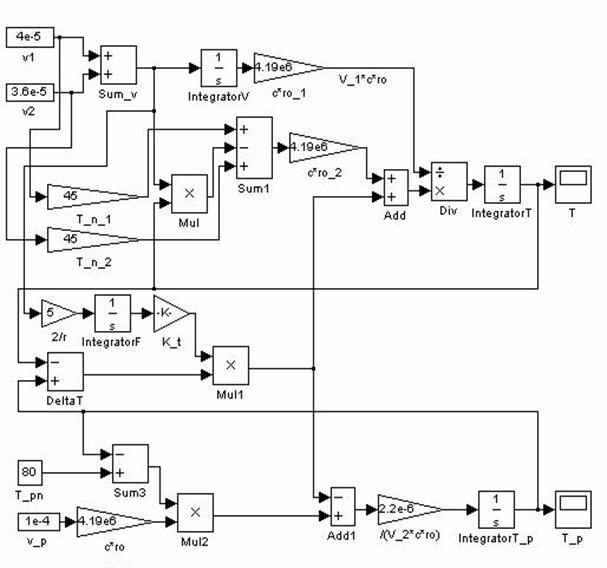
Рисунок 2.5 – Тепловая модель объекта
В модели все величины указаны в системе СИ. При моделировании было учтено, что площадь теплопередачи является величиной переменной и равна площади соприкосновения раствора со стенкой аппарата.
Для установления начальных условий для величин использовались данные из пункта 1.2. Начальный объем реакционной смеси принят 0.2 л. Номинальные расходы реагентов приняты соответствующими номинальному режиму для пункта 2.1. Температура воды на входе в рубашку принята 80 °С.
Для вычисления площади теплообмена были использованы следующие соображения. Дно аппарата представляет собой эллипсоид вращения, т.е эллипсоид с двумя равными полуосями (см. рисунок 2.6).

Рисунок 2.6 – Конструкция аппарата
Численные значения длин полуосей: a
= 0.15 м, b
= 0.4 м.
Известно, что в начальный момент объем смеси составлял 0.2 л. Этот объем можно представить условно как сумму двух объемов: в эллиптической части аппарата (до уровня h0
= a
) – Vэ
, и в цилиндрической части (hдоп
) – V
ц
. Для того, чтобы рассчитать начальное условие F0
, нужно, очевидно, знать hдоп
. Общий объем:
V0
= V
э
+ V
ц
Объем Vэ
найдем как следствие из формулы объема эллипсоида:
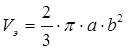 , ,
откуда Vэ
= 0.05 м3
. Тогда Vц
= 0.15 м3
. Учтем, что этот объем вычисляется по формуле:
 , ,
откуда легко найти, что hдоп
= 0.3 м.
В свою очередь, начальное условие для площади можно записать в аналогичном виде:
F0
= F
э
+ F
ц
.
Для вычисления F
э
воспользуемся уравнением эллипса. Площадь поверхности эллипсоида найдем как площадь фигуры, полученной путем вращения одной половины эллипса вокруг оси. Уравнение эллипса:
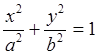 , (2.12) , (2.12)
формула для нахождения площади:
 . (2.13) . (2.13)
 Выразим из (2.12) y
и подставим в (2.13). Преобразуем полученное выражение, учтя, что a
< b
. В результате получаем: Выразим из (2.12) y
и подставим в (2.13). Преобразуем полученное выражение, учтя, что a
< b
. В результате получаем:
 . .
Данный интеграл берется с помощью тригонометрической подстановки
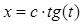 , , 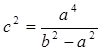 . .
Пропустив промежуточные выкладки, приведем конечный результат:
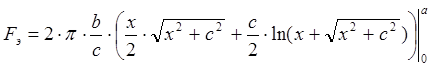 . (2.14) . (2.14)
Для вычисления Fц
воспользуемся формулой:
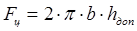 . (2.15) . (2.15)
Проведя вычисления по формулам (2.14) и (2.15), найдем начальное условие для площади теплообмена F0
= 1.381 м2
.
Чтобы вычислить площадь теплообмена как функцию времени, воспользуемся следующими соображениями. За некоторое малое время Δt
при подаче реагентов в реактор уровень в нем повысится на некоторую малую величину Δh
. При этом площадь теплообмена и объем тоже получат приращения:
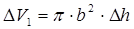 ; ;  . .
Выразив из второго выражения Δh
и подставив его в первое, получим:
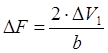 . .
Устремляя Δt
к нулю и интегрируя, получим:
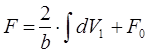 . (2.16) . (2.16)
Величина dV1
легко выражается из (2.9).
Для нахождения коэффициента теплопередачи воспользуемся формулой:
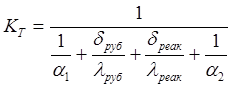 , (2.17) , (2.17)
в которой приняты следующие обозначения:
α1
– коэффициент теплоотдачи от воды в рубашке к стенке рубашки;
δруб
– толщина стенки рубашки;
λруб
– коэффициент теплопроводности стенки рубашки;
δреак
– толщина стенки реактора;
 λреак
– коэффициент теплопроводности стенки реактора; λреак
– коэффициент теплопроводности стенки реактора;
α2
– коэффициент теплоотдачи от стенки реактора к реакционной смеси.
Для вычисления α1
воспользуемся критерием Нуссельта, характеризующим конвективный теплообмен между жидкостью и поверхностью твердого тела:
 , (2.18) , (2.18)
где λ
– коэффициент теплопроводности теплоносителя;
d
– определяющий размер.
Здесь в качестве определяющего размера необходимо принять эквивалентный диаметр трубы, обладающей таким же сечением, что и пространство внутри рубашки. Внутренний диаметр реактора 0.8 м, наружный – 0.9 м, толщина стенок рубашки и реактора – 0.006 м. Вычислив площадь кольца, найдем диаметр эквивалентной трубы: d
=0.36 м. Коэффициент теплопроводности воды λ
= 65.9 Вт/(м2
·
K)
. Для нахождения критерия Nu
определим характер течения жидкости в рубашке. Это можно сделать, рассчитав критерий Рейнольдса по формуле:
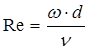 , (2.19) , (2.19)
где ω
– линейная скорость движения жидкости в трубе;
d
– определяющий размер;
ν
– кинематическая вязкость среды.
Приняв расход воды 1.5·
10-4
м3
/с, диаметр подводящей трубы 20 мм, рассчитаем линейную скорость воды в рубашке при максимальном напоре: ω
= 0.5 м/с. Кинематическую вязкость при температуре 80 °С примем равной 0.478·
10-6
м2
/с. Из (2.19) получаем Re
= 14000. Следовательно, режим течения – турбулентный. Поэтому критерий Нуссельта вычисляется по формуле [3, с.160]:
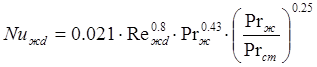 . (2.20) . (2.20)
Проведя вычисления по этой формуле, получаем Nuж
d
= 89.7. Подставив полученное значение в (2.18), получаем α1
= 16417 Вт/(м2
·
K)
.
Количественно определить характер движения жидкости в реакторе сложнее, т.к. присутствует мешалка. Можно предположить, что характер движения – турбулентный, обусловленный интенсивным перемешиванием. Среда в реакторе представляет собой сильно разбавленный водный раствор желатины и солей щелочных металлов, поэтому приближенно принимаем условия теплоотдачи от стенки реактора аналогичными условиям теплоотдачи в рубашке и считаем, что α2
= α1
= 16000 Вт/(м2
·
K)
.
Второе и третье слагаемые в знаменателе (2.17) равны, т.к. толщина стенок реактора равна толщине стенок рубашки – 6 мм. Стенки рубашки и реактора сделаны из стали 12Х18Н10Т, ее коэффициент теплопроводности λ
= 16.88 Вт/(м·
K)
.
 Подставив все полученные величины в (2.17), получим, что K
Т
= 1200 Вт/(м2
·
K)
. Подставив все полученные величины в (2.17), получим, что K
Т
= 1200 Вт/(м2
·
K)
.
После всех этих выкладок необходимо получить разгонные кривые объекта по каналам возмущения и управления. В качестве возмущения определим температуру поступающих в реактор исходных веществ, а в качестве управляющего воздействия – расход воды на входе в рубашку.
Для получения передаточной функции по возмущению считаем, что изменение температуры одного из входных растворов на 5 °С является максимальным, т.е соответствует единице в относительном масштабе, а изменение температуры в реакторе на 1 °С соответствует максимальному отклонению выходной величины.
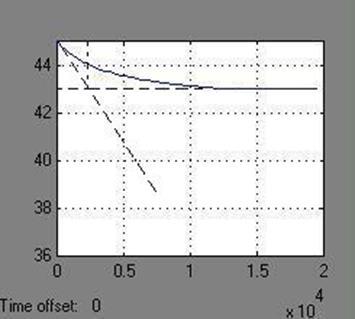
Рисунок 2.7 – Разгонная кривая по возмущению
Видно, что выходная температура изменилась на 2 °С. Следовательно, коэффициент усиления этого звена равен 2. По виду разгонной кривой можно предположить, что это звено можно удовлетворительно описать как инерционное звено 1 порядка. Определив постоянную времени графическим способом (см. рисунок 2.7), получаем, что T
≈ 0.2·
104
с ≈ 33 мин.
На основании этого запишем передаточную функцию объекта по второй регулируемой величине – температуре по каналу возмущения:
 (2.21) (2.21)
 Для получения передаточной функции по управлению считаем, что подача в рубашку воды из магистрали с расходом 1.5·
10-4
м3
/с является максимальной, т.е. соответствует единице в относительном масштабе, а изменение температуры в реакторе на 1 °С по-прежнему соответствует максимальному отклонению выходной величины. Для получения передаточной функции по управлению считаем, что подача в рубашку воды из магистрали с расходом 1.5·
10-4
м3
/с является максимальной, т.е. соответствует единице в относительном масштабе, а изменение температуры в реакторе на 1 °С по-прежнему соответствует максимальному отклонению выходной величины.
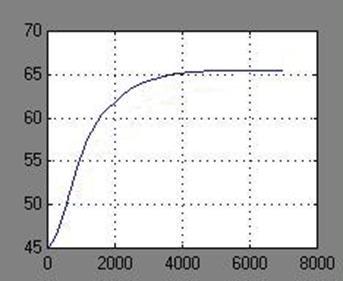
Рисунок 2.8 – Разгонная кривая по управлению
Видно, что выходная температура изменилась на 20 °С. Следовательно, коэффициент усиления этого звена равен 20. По виду разгонной кривой можно предположить, что это звено можно удовлетворительно описать как инерционное звено 2 порядка.
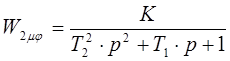 (2.21) (2.21)
Найдем постоянные времени этого звена аналитическим методом. Для этого воспользуемся тем, что полученная переходная функция удовлетворяет дифференциальному уравнению, описывающему наше звено:
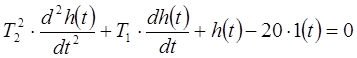 . (2.22) . (2.22)
Предположим, что для функции h(t)
известно аналитическое выражение. Тогда необходимо найти такие значения T1
и T2
, при которых равенство (2.22) выполнялось бы наиболее точно. Это можно сделать, если составить так называемую функцию невязки
, т.е. критерий, характеризующий отклонение левой части (2.22) от нуля. Если такая функция будет являться положительной и будет иметь единственный экстремум, являющийся одновременно ее минимумом, то, найдя его, можно будет считать задачу выполненной.
 В теории оптимизации доказывается, что в качестве описанного критерия может использоваться такая функция: В теории оптимизации доказывается, что в качестве описанного критерия может использоваться такая функция:
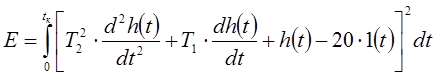 . (2.23) . (2.23)
Здесь в качестве верхнего предела интегрирования взято время окончания переходного процесса. Эта функция обладает рядом неплохих свойств, и одно из них – то, что необходимые условия минимума для этой функции являются и достаточными. Из этого следует, что, приравняв ее частные производные по T1
и T2
к нулю, мы достоверно получим искомую оптимальную точку. Кроме того, после нахождения частных производных мы получаем линейную систему уравнений относительно T1
и T2
2
.
Для нахождения аналитического выражения переходной функции можно воспользоваться любым из методов приближения функций, однако мы предпочтем метод наименьших квадратов. Составив по рисунку 2.8 таблицу значений неизвестной функции, аппроксимируем ее полиномом 4-й степени. Текст программы аппроксимации приведен в приложении А. Был получен следующий результат:

На основе (2.23) была получена система линейных уравнений следующего вида:

Ее коэффициенты вычисляются по следующим формулам:
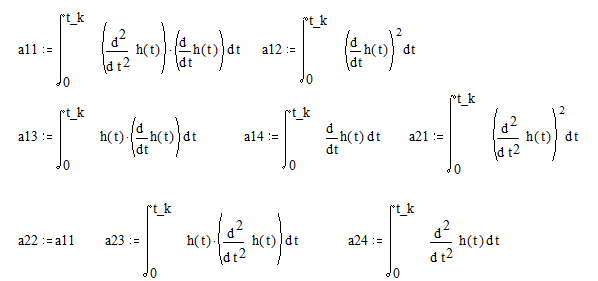
Решив (2.25), нашли, что T1
= 22.6 мин, T2
= 8.38 мин.

3 ВЫБОР И ОБОСНОВАНИЕ РЕГУЛИРУЕМЫХ ВЕЛИЧИН И РЕГУЛИРУЮЩИХ ВОЗДЕЙСТВИЙ
Исходя из технологического описания процесса (см. пункт 1.2), была выявлена цель автоматизации – поддержание на постоянном уровне с максимально возможной точностью двух основных технологических параметров процесса – температуры и pBr
в аппарате. В качестве регулируемых выбираем именно эти две величины.
На основе проведенного моделирования можно выявить как минимум по 2 внешних величины, влияющих на рассмотренные регулируемые величины.
На величину pBr
в аппарате влияют: концентрация и скорость подачи каждого из реагентов. Управлять концентрацией какого-либо из реагентов затруднительно, т.к. их растворы приготавливаются заранее в специальных сборниках-термостатах, откуда потом они подаются в аппарат. Поэтому мы условились принимать эти концентрации за неконтролируемые возмущения. Подача каждого из реагентов контролируется своим перистальтическим насосом, приводимым в движение двигателем постоянного тока независимого возбуждения. Благодаря этому возможно регулирование расхода в пределах 50% от максимального вниз от максимума. Кроме того, мы выяснили, что для поддержания нужного режима необходимо один из реагентов (KBr
) подавать в избытке. Тогда логично сделать регулируемой подачу второго реагента (AgNO3
). Изменяя его расход, можно будет эффективно управлять величиной pBr
в аппарате.
На величину температуры в аппарате влияют объемные расходы реагентов, а также температура и расход теплоносителя в рубашке. Расходы реагентов влияют на температуру в меньшей степени. Температуры реагентов на входе в аппарат полностью определяются температурами в сборниках-термостатах. Однако по пути в реактор они могут охладиться. Поэтому за неконтролируемое возмущение мы приняли температуру реагентов на входе в аппарат. Температуру воды в магистралях теплоносителей считаем постоянной, а именно, в магистрали горячей воды +80 °С, в магистрали холодной воды +20 °С. Поэтому логично управлять температурой в аппарате, изменяя подачу в рубашку горячего или холодного теплоносителя. Это можно делать с помощью регулирующих клапанов.
4  ФОРМИРОВАНИЕ СТРУКТУРЫ СИСТЕМЫ УПРАВЛЕНИЯ ФОРМИРОВАНИЕ СТРУКТУРЫ СИСТЕМЫ УПРАВЛЕНИЯ
В соответствии с моделированием, можно следующим образом представить структурную схему объекта управления:
Рисунок 4.1 – Структурная схема объекта
В объекте отсутствуют перекрестные связи между регулируемыми величинами, поэтому будущая САУ может быть представлена как совокупность двух независимых систем с одной регулируемой величиной. Использование многосвязанной САУ в данном случае представляется нецелесообразным.
Рассмотрим 4 возможных варианта организации САУ с одной регулируемой величиной. Все схемы изображены упрощенно, не показаны датчики, исполнительные механизмы и регулирующие органы.
1) 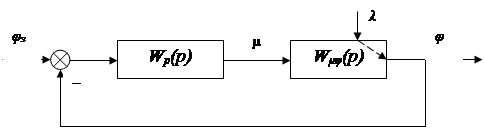 простая одноконтурная система простая одноконтурная система
Рисунок 4.2 – Упрощенная структура одноконтурной системы
2) 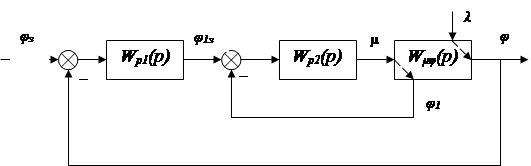 каскадная система управления каскадная система управления
Рисунок 4.3 – Структура каскадной системы

3) двухконтурная система с дополнительным сигналом
Рисунок 4.3 – Структура системы с дополнительным сигналом
4) система с компенсацией возмущений
Рисунок 4.4 – Структура системы с компенсацией возмущений
Каскадная система применяется в том случае, когда по основному каналу воздействия объект является сильно инерционным, однако есть некоторая вспомогательная величина объекта, которая откликается на возмущения и на регулирующее воздействие со значительно меньшей инерционностью. При этом часто может оказаться, что контроль этой вспомогательной регулируемой величины является вовсе не обязательным для того, чтобы поддерживать надлежащим образом режим объекта. Но введением в схему системы регулирования такого дополнительного воздействия, как правило, удается получить значительное улучшение качества регулирования. В нашем случае использование этой схемы могло бы принести пользу, однако в объекте отсутствуют такие промежуточные величины, по которым можно было бы построить каскадную систему.
Система, изображенная на рисунке 4.3, после структурных преобразований становится практически аналогичной каскадной схеме. Она далее не рассматривается по той же причине, что и каскадная.
Система, изображенная на рисунке 4.4, может быть применена в том случае, когда возмущения являются контролируемыми, т.е. их можно измерить и на этой основе построить контур компенсации. В нашем случае контролировать возмущения весьма затруднительно, поэтому и эта схема отвергается.
 На основе вышеизложенного в качестве наиболее подходящей принята структура САУ в виде двух простых одноконтурных систем. Общая схема одного контура такой системы подробно изображена на рисунке 4.5. На основе вышеизложенного в качестве наиболее подходящей принята структура САУ в виде двух простых одноконтурных систем. Общая схема одного контура такой системы подробно изображена на рисунке 4.5.
Рисунок 4.5 – Структура одноконтурной системы управления
5  РАСЧЕТ ЭЛЕМЕНТОВ И ПАРАМЕТРОВ СИСТЕМЫ РАСЧЕТ ЭЛЕМЕНТОВ И ПАРАМЕТРОВ СИСТЕМЫ
5.1 Расчет и выбор регулирующего органа для расхода воды
Рассчитаем и выберем РО для регулирования расхода воды из магистрали в рубашку аппарата. Схема трубопроводов для подвода воды изображена на рисунке 5.1.
Рисунок 5.1 – Схема трубопроводов для теплоносителя
На рисунке изображен ввод в магистраль (слева внизу), два поворота трубы под 90° радиусом R = 0.1 м, два отсечных и один регулирующий клапан, а также ввод в рубашку. Трубопровод состоит из трех участков с длинами 4, 5 и 1 м.
Приведем другие технологические данные, необходимые для расчета: максимальный объемный расход vmax
= 10-4
м3
/с
, внутренний диаметр трубы D
= 20 мм, шероховатость трубы по справочнику [4, c.272] принимаем n1
= 0.1 мм. Давление в магистрали p0
= 0.4 МПа, давление в рубашке pруб
= 0.15 МПа. Плотность воды ρ
= 1000 кг/м3
. Кинематическая вязкость воды при 80 °С ν
= 0.328·
10-6
м2
/с
.
Порядок расчета следующий [4, с. 269]:
1) гидростатический напор, соответствующий разности высот Δh
: 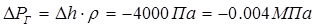
2) определяем потери давления в линии. Для этого найдем
перепад давлений в сети:
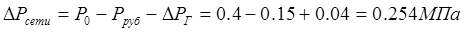 . .
Определяем число Рейнольдса при максимальном расходе:
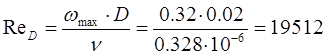
Определяем условие гидравлической гладкости трубопровода:
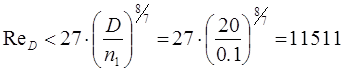 . .
 Трубопровод не является гидравлически гладким, поэтому коэффициент гидравлического сопротивления λ
определяется по рисунку 6.21 в [3, с.275]. λ
= 0.0326. Трубопровод не является гидравлически гладким, поэтому коэффициент гидравлического сопротивления λ
определяется по рисунку 6.21 в [3, с.275]. λ
= 0.0326.
Общая длина трубопровода L
= 10 м. Находим потерю давления на прямых участках трубопровода:
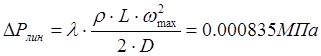 . .
Определим потери давления в местных гидравлических сопротивлениях трубопровода. По таблице 6.8 [2, с.271] определяем: ε
вх
= 0.5, ε
вых
= 1, ε90
= 0.6, ε
отсеч
= 8.0. Тогда суммарные потери равны:
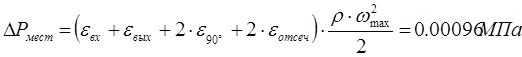 . .
Находим суммарные потери в линии:
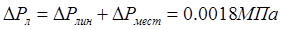
3) находим перепад давлений на регулирующем органе: 
4) определяем максимальную пропускную способность клапана: 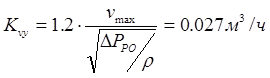 . .
5) в каталоге отсутствует РО со столь малым Kv
у
. Поэтому
выбираем односедельный РО: ПОУ-7, Dу
= 15 мм, Kv
у
= 0.1.
6) определяем значение критерия Рейнольдса для выбранного РО: 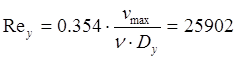 . .
Т.к. Reу
> 2000, то влияние вязкости на расход не учитываем и выбранный РО проверяем на возможность возникновения кавитации.
7) определяем коэффициент сопротивления РО: 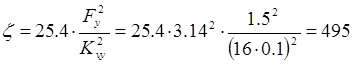
По кривой 3 на рисунке 6.23 [3, с. 277] определяем, что максимальный коэффициент кавитации Kкав
max
= 0.55
8) определим перепад давлений, при котором возникает
кавитация. При этом учтем, что абсолютное давление насыщенных паров воздуха при температуре 80 °С равно P
нщ
= 0.047 МПа, а давление перед РО приблизительно равно давлению в магистрали.
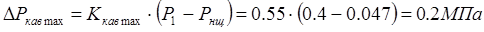
9) определяем максимальную пропускную способность: 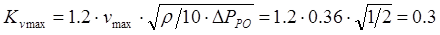
 Т.к. Kv max
> Kv
у
для выбранного РО, то он будет работать в режиме кавитации и не обеспечит заданного расхода жидкости. Поэтому выбираем из каталога РО ПОУ-7 с D
у
= 15 мм, Kv
у
= 0.5. Т.к. Kv max
> Kv
у
для выбранного РО, то он будет работать в режиме кавитации и не обеспечит заданного расхода жидкости. Поэтому выбираем из каталога РО ПОУ-7 с D
у
= 15 мм, Kv
у
= 0.5.
10) выберем вид расходной характеристики клапана. Согласно
модели, основными возмущениями в объекте являются внешние возмущения, которые не действуют по регулирующему каналу. Поэтому по условиям процесса желательна линейная характеристика. Рассчитаем отношение перепада давлений в линии к перепаду давлений на РО:
 . .
Поскольку n
< 1.5, то окончательно останавливаем свой выбор на клапане с линейной расходной характеристикой.
Для последующего анализа системы необходимо знать передаточные функции клапана и исполнительного механизма. В качестве исполнительного механизма можно использовать стандартный механизм типа МИМ-1 прямого действия совместно с позиционером. Его передаточную функцию можно описать как инерционное звено 1 порядка с единичным коэффициентом усиления. Его инерционность обусловлена емкостью соединительных трубопроводов и камеры переменного объема. Обычно эта инерционность лежит в пределах 5 – 20с, поэтому принимаем TИМ
= 0.1 мин.
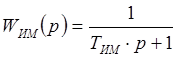 (5.1) (5.1)
Так как был выбран РО с условной пропускной способностью в 18 раз большей, чем РО, соответствующий выбранному нами единичному расходу, то РО будем считать усилительным звеном с коэффициентом усиления KРО
=18.
 (5.2) (5.2)
5.2 Выбор регулирующего органа для расхода реагентов
Как было указано в пункте 2.1, подача реагентов в аппарат осуществляется с помощью перистальтических насосов, приводимых в движение двигателями постоянного тока независимого возбуждения. Такой выбор обусловлен прежде всего жесткими ограничениями, накладываемыми на скорость и качество подачи реагентов. А именно, необходимо поддерживать беспульсационный режим течения. Кроме того, нежелательность использования клапанов вытекает из высоких требований к чистоте растворов. Для их подачи используются трубки из поливинилхлорида. Характерной особенностью перистальтического насоса является отсутствие соприкосновения жидкости с металлом. Этим и объясняется наш выбор.
 Для управления частотой вращения двигателя постоянного тока применяется электропривод типа ЭТУ, имеющий вход для унифицированного сигнала постоянного тока. Регулирование частоты вращения при этом возможно вниз по электромеханической характеристике на 50% от максимального значения. Для управления частотой вращения двигателя постоянного тока применяется электропривод типа ЭТУ, имеющий вход для унифицированного сигнала постоянного тока. Регулирование частоты вращения при этом возможно вниз по электромеханической характеристике на 50% от максимального значения.
В динамическом отношении двигатель является апериодическим звеном первого порядка. Электронное устройство управления является безынерционным звеном с единичным коэффициентом усиления. Постоянную времени электродвигателя принимаем 0.1 мин. T
ИМ
= 0.1.
5.3 Расчет и выбор измерительных преобразователей
Основой для выбора преобразователей является достижение требуемой точности измерений. В нашем случае есть два контура регулирования – pBr
и температуры, и для каждого применяется свой комплект датчиков и измерительных преобразователей.
5.3.1 Выбор комплекта для измерения pBr
Для измерения pBr
в реакторе выбираем комплект, состоящий из датчика погружного ДПг-4М-2-1600 и нормирующего преобразователя типа П-201. В качестве сравнительного электрода применяется непроточный хлорсеребряный электрод 5268, в качестве измерительного – аргентитовый электрод ЭА-2-220. Пределы измерений устанавливаются на приборе П-201 с помощью специальных перемычек. В нашем случае выбираем пределы 1 – 7 единиц pBr
. Рабочая температура в пределах +5…+70 °С. Время установления сигнала преобразователя < 10 с. Поэтому принимаем передаточную функцию датчика и нормирующего преобразователя в виде апериодического звена первого порядка.
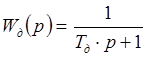 , ,
где Tд
= 0.05 мин.
Для регистрации pBr
используется автоматический самопишущий мост типа КСУ-1М. Рассчитаем пределы погрешности измерительного комплекта для регистрации pBr
. Схема комплекта приведена на рисунке 5.2.
Рисунок 5.2 – Схема комплекта для измерения pBr
Значение pBr
, регистрируемое мостом, будет равно: (pBr
д
±
ΔpBr
), где pBrд
– действительное значение pBr
, ΔpBr
– абсолютная погрешность измерения. Эта погрешность вычисляется по формуле:
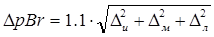 , (5.3) , (5.3)
 где Δи
– инструментальная погрешность; где Δи
– инструментальная погрешность;
Δм
– методическая погрешность;
Δл
– личная погрешность.
Личную составляющую погрешности определим как половину цены деления шкалы вторичного прибора Δл
= 0.1 pBr.
Инструментальная погрешность: Δи
= δи
·
ΔN1
. В свою очередь, относительная погрешность вычисляется по формуле:
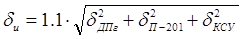 , (5.4) , (5.4)
относительные погрешности отдельных элементов комплекта вычисляются по формулам:
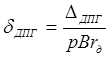 , (5.5) , (5.5)
где ΔДПГ
– абсолютная погрешность датчика, ±0.1 pBr;
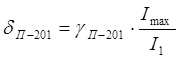 , (5.6) , (5.6)
где γП-201
– приведенная погрешность вторичного преобразователя, 0.01;
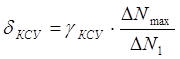 , (5.7) , (5.7)
где γКСУ
– приведенная погрешность моста, 0.005.
Проведя вычисления по этим формулам, получаем: δДПГ
= 0.045, δП-201
= 0.018, δКСУ
= 0.009. Подставив полученные значения в (5.4), получаем δи
= 0.054. Абсолютная погрешность Δи
= 0.12 pBr.
Методическую погрешность принимаем равной нулю, т.к. статические характеристики датчика и вторичного прибора являются линейными.
Подставляя полученные результаты в (5.3), получаем значение абсолютной погрешности измерения pBr
: ΔpBr
= 0.15 pBr.
Полученное значение меньше, чем диапазон требуемой точности поддержания величины pBr
в аппарате. Поэтому выбранный нами комплект удовлетворяет требованиям процесса с метрологической точки зрения.
5.3.2 Выбор комплекта для измерения температуры
Для измерения температуры в реакторе и в рубашке выбираем термопреобразователь сопротивления типа ТСП-0879-01 со статической характеристикой 50П. Пределы измерения: –50…+250 °С. Рабочее давление – не выше 0.4 МПа. Инерционность – 30…40 с. На основании этого принимаем постоянную времени датчика 0.2 мин.
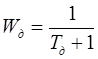
 В будущем планируется использовать регулятор типа Р17.2, имеющий входы для двух сигналов от термопреобразователей сопротивления. Поэтому в использовании нормирующих преобразователей надобности нет. Для регистрации температуры используется автоматический самопишущий мост типа КСМ-4, имеющий вход для сигнала от термопреобразователя сопротивления. В будущем планируется использовать регулятор типа Р17.2, имеющий входы для двух сигналов от термопреобразователей сопротивления. Поэтому в использовании нормирующих преобразователей надобности нет. Для регистрации температуры используется автоматический самопишущий мост типа КСМ-4, имеющий вход для сигнала от термопреобразователя сопротивления.
Рассчитаем пределы погрешности измерительного комплекта для регистрации температуры. Схема комплекта приведена на рисунке 5.3.
Рисунок 5.3 – Схема комплекта для измерения температуры
Значение температуры, регистрируемое мостом, будет равно (t
д
±
Δt
), где tд
– действительное значение температуры, Δt
– абсолютная погрешность измерения.
Эта погрешность вычисляется по формуле:
 , (5.8) , (5.8)
где Δи
– инструментальная погрешность;
Δм
– методическая погрешность;
Δл
– личная погрешность.
Личную составляющую погрешности определим как половину цены деления шкалы вторичного прибора Δл
= 0.5 °С.
Инструментальная погрешность: Δи
= δи
·
ΔN1
. В свою очередь, относительная погрешность вычисляется по формуле:
 , (5.9) , (5.9)
относительные погрешности отдельных элементов комплекта вычисляются по формулам:
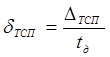 , (5.10) , (5.10)
где ΔТСП
– абсолютная погрешность датчика, ±1 °С;
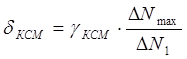 , (5.12) , (5.12)
где γКСУ
– приведенная погрешность моста, 0.005.
Проведя вычисления по этим формулам, получаем: δТСП
= 0.022, δКСМ
= 0.011. Подставив полученные значения в (5.4), получаем δи
= 0.027. Абсолютная погрешность Δи
= 1.2 °С.
Методическая составляющая погрешности возникает по причине незначительной нелинейности статической характеристики термопреобразователя и вычисляется как отклонение измеренного значения температуры от истинного:
 Δм
= N1
- t
д
. (5.13) Δм
= N1
- t
д
. (5.13)
Пусть измеренное значение равно N1
= 45 °С. Пределы измерения температуры мостом равны 0…100 °С. Тогда чувствительность моста равна
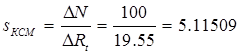 °С/Ом. °С/Ом.
Тогда
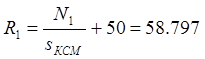 Ом. Ом.
Действительное значение температуры найдем из статической характеристики датчика ТСП, имеющей вид:
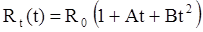 , ,
где 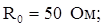
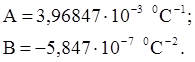
Из статической характеристики получаем, что t
= 44.628 °С. Тогда по формуле (5.13) получаем, что Δм
= 0.372 °С.
Подставляя полученные результаты в (5.8), получаем значение абсолютной погрешности измерения температуры: Δt
= 1.5 °С.
Полученное значение больше, чем диапазон требуемой точности поддержания температуры в аппарате. Однако выбранный комплект используется только для регистрации температуры, в измерительной цепи регулятора используется только один термопреобразователь сопротивления.
5.4 Выбор и обоснование регуляторов. Расчет настроек.
Получив ранее передаточные функции всех звеньев САУ и выяснив структуру системы, необходимо подобрать вид передаточной функции и параметры настройки регулятора так, чтобы обеспечить наилучшие статические и динамические характеристики всей системы в целом. Сформулируем основные требования к качеству переходных процессов для нашей системы:
– отсутствие статической ошибки;
– минимальная колебательность, желательно апериодичность;
– минимальное время регулирования.
Надо отметить, что перечисленные требования довольно трудно формализовать в виде одного критерия, поэтому выбираем наиболее “близкий” по смыслу критерий – а именно, квадратичный интегральный критерий вида:
 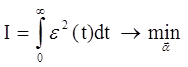 , (5.14) , (5.14)
где a = (a1
,a2
,...) – вектор настраиваемых параметров САУ. Поскольку ошибка имеет две составляющие – по управлению и по возмущению – то на основе (5.14) получаем две формулы для вычисления критерия:
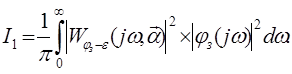 , (5.15) , (5.15)
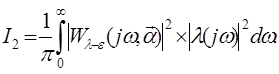 . (5.16) . (5.16)
В приведеных формулах верхний предел интегрирования можно заменить на время переходного процесса в системе.
Надо отметить, что применение данного критерия часто может привести к получению таких настроек, при которых система окажется неустойчивой. Однако квадратичная ошибка при этом будет действительно минимальной. Избежать этого можно, если ввести ограничения на варьируемые при оптимизации переменные. В качестве основы для ограничений удобно принять критерий Гурвица. Он дает систему алгебраических ограничений на коэффициенты характеристического уравнения, что дает возможность использовать полученные ограничения при оптимизации. При этом количество ограничений будет зависеть от степени характеристического уравнения, оно будет равно n-1, где n – его степень.
Для оптимизации по приведенным критериям будем использовать функцию Minimize
из пакета Mathcad 2000
.
5.4.1 Расчет регулятора для pBr
В качестве базового будем рассматривать аналоговый регулятор типа Р17, входящий в систему “Каскад-2”. Он обеспечивает суммирование, гальваническое разделение, масштабирование до четырех унифицированных сигналов постоянного тока, а также введение сигнала задания от внутреннего или внешнего потенциометрического задатчика, двухстороннее регулируемое ограничение и демпфирование выходного сигнала. Выходной сигнал – непрерывный 0…5 мА. Передаточная функция регулятора имеет вид:
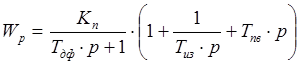 , (5.17) , (5.17)
где Kп
– коэффициент передачи;
Tиз
– время изодрома;
Tпв
– время предварения;
Tдф
– время демпфирования.
 При желании можно реализовывать П-ПИ-ПД-ПИД законы с демпфированием и без. При желании можно реализовывать П-ПИ-ПД-ПИД законы с демпфированием и без.
Передаточная функция по каналу φз
– φ
:
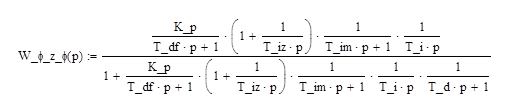 ; ;
передаточная функция по каналу λ – φ
:
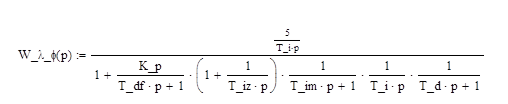 . .
Следует отметить, что в рассматриваемом контуре нельзя использовать П-регулятор. Несмотря на то, что объект является астатическим по управлению, и, следовательно, при использовании даже П-регулятора не будет возникать статической ошибки по управлению, переходный процесс по возмущению не будет приходить в ноль. То есть, система не будет отрабатывать возмущения. Действительно, найдя изображение выходной величины по каналу λ – φ
, получим:
 . .
Поэтому пробуем вариант с ПИ-регулятором. Выяснив, что наиболее “опасным” каналом является возмущение, оптимизацию будем производить по критерию (5.16) с ограничениями на устойчивость системы. Результаты оптимизации: Kп
= 40, T
из
= 10 мин. Значение критерия I2
равно 0.081. Переходный процесс по возмущению при заданных настройках приведен на рисунке 5.4 (здесь и в дальнейшем числа по оси x
– в минутах).
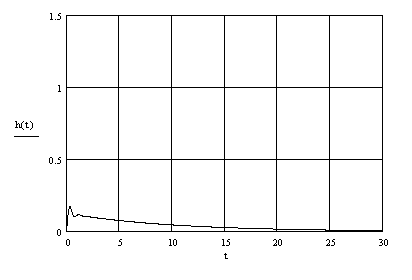
Рисунок 5.4 – Переходный процесс по λ
в контуре pBr
с ПИ- регулятором

Поскольку регулятор обладает более широкими возможностями настройки, проверим систему с другими видами передаточных функций.
Рассмотрим систему с ПИ- регулятором с демпфированием. Его передаточная функция равна:
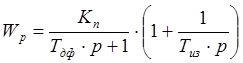
Записав передаточную функцию по каналу λ
– ε
, выполним оптимизацию критерия (5.16). Результаты оптимизации: K
п
= 35, T
из
= 15 мин, Tдф
= 0.1 мин. Значение критерия I2
равно 0.163. Переходный процесс по возмущению при заданных настройках приведен на рисунке 5.5.
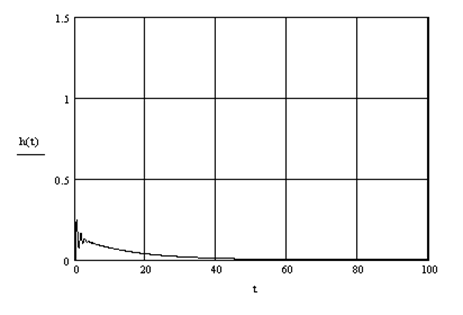
Рисунок 5.5 – Переходный процесс по λ
в контуре pBr
с ПИ- регулятором с демпфированием
Видим, что длительность переходного процесса несколько увеличилась, и увеличилась колебательность, что отразилось на ухудшении квадратичного критерия. Для улучшения динамических характеристик можно ввести дифференциальную составляющую в закон регулирования. Поэтому рассмотрим систему, использующую все возможности регулятора, который при этом имеет передаточную функцию (5.17). Записав передаточную функцию по каналу λ
– ε
, выполним оптимизацию критерия (5.16). Результаты оптимизации: K
п
= 3.5, T
из
= 0.7 мин, Tпв
= 0.26 мин, Tдф
= 0.196 мин. Значение критерия I2
равно 1.342. Переходный процесс по возмущению при заданных настройках приведен на рисунке 5.6.
 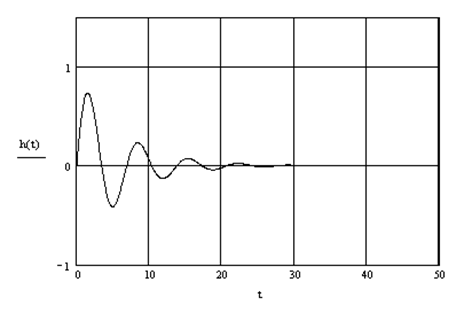
Рисунок 5.6 – Переходный процесс по λ
в контуре pBr
с ПИД- регулятором с демпфированием
Видим, что динамические показатели и критерий сильно ухудшились. Поэтому для реализации окончательно принимаем ПИ- регулятор с настройками, найденными ранее. Для проверки корректности работы системы построим переходный процесс по управлению. Значение критерия I1
при найденных настройках равно 0.356. Переходный процесс в такой системе по каналу задание – выходная величина изображен на рисунке 5.7.

Рисунок 5.7 – Переходный процесс по μ
в контуре pBr
с ПИ- регулятором
5.4.2  Расчет регулятора для температуры Расчет регулятора для температуры
В качестве базового будем рассматривать регулятор Р17.2, являющийся модификацией регулятора, описанного в предыдущем пункте. Наш выбор обусловлен тем, что у этой модификации присутствуют 2 входа для сигналов с термопреобразователей сопротивления, благодаря чему отпадает надобность в промежуточных преобразователях. В остальном эти два регулятора полностью совпадают.
В данном контуре объект представляет собой статическое звено, поэтому наша задача – достичь требуемого качества переходного процесса при отсутствии статической ошибки регулирования.
Передаточная функция по каналу φз
– φ
:
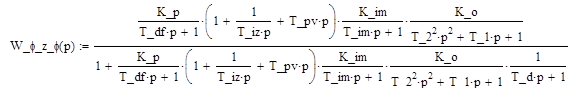 , ,
передаточная функция по каналу λ – φ
:
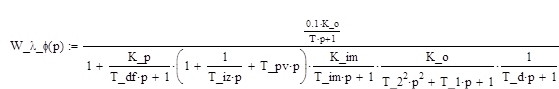
Рассмотрим П- регулятор. При реализации такой системы неизбежна статическая ошибка, поскольку и регулятор, и объект являются статическими звеньями. Действительно, найдя изображение ошибки по каналу управления, получим:
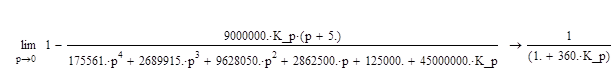 Построим переходный процесс по μ
в полученной системе. Переходный процесс изображен на рисунке 5.8. Настройка регулятора Kп
= 0.03. Построим переходный процесс по μ
в полученной системе. Переходный процесс изображен на рисунке 5.8. Настройка регулятора Kп
= 0.03.
 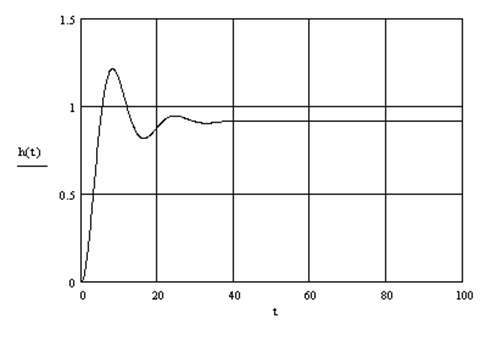
Рисунок 5.8 – Переходный процесс по μ
в контуре t
с П- регулятором
Из-за наличия статической ошибки П- регулятор далее не рассматривается.
Рассмотрим систему с ПИ- регулятором. Оптимизацию будем проводить по критерию (5.15) с ограничениями на устойчивость системы. Результаты оптимизации: K
п
= 0.003, T
из
= 18 мин. Численное значение критерия I1
равно 1.283. Переходный процесс по μ изображен на рисунке 5.9.
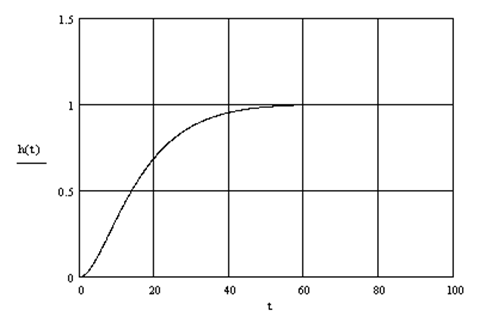
Рисунок 5.9 – Переходный процесс по μ
в контуре t
с ПИ- регулятором
Видим, что использование интегральной составляющей позволило добиться отсутствия колебаний, но увеличило время регулирования. Для устранения этого недостатка в закон регулирования часто вводят дифференциальную составляющую. Поэтому рассмотрим систему с ПИД- регулятором. Его передаточная функция описывается уравнением (5.17) при Tдф
=0. Оптимизируем настройки по критерию (5.15) с ограничениями на устойчивость системы. Были получены результаты: Kп
= 0.004, T
из
= 18 мин, Tпв
= 0.5 мин. Численное значение критерия I1
равно 1.077. Переходный процесс по μ изображен на рисунке 5.10.
 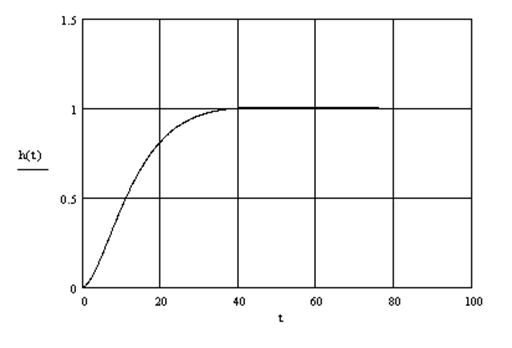
Рисунок 5.10 – Переходный процесс по μ
в контуре t
с ПИД- регулятором
Видим, что немного уменьшилось время регулирования и интегральная ошибка. Следовательно, применение дифференциальной составляющей в данном случае оправдано.
Исследуем систему, реализующую все возможности регулятора, который при этом имеет передаточную функцию (5.17). Записав передаточную функцию по каналу φз
– ε
, выполним оптимизацию критерия (5.15). Результаты оптимизации: K
п
= 0.004, T
из
= 17 мин, Tпв
= 0.5 мин, Tдф
= 0.5 мин. Значение критерия I1
равно 1.120. Переходный процесс по управлению при заданных настройках приведен на рисунке 5.11.
 
Рисунок 5.11 – Переходный процесс по μ
в контуре t
с ПИД- регулятором и с демпфированием
Видим, что удалось еще более уменьшить время переходного процесса, но появилось небольшое перерегулирование. Однако величина динамического заброса очень мала, что дает основания предпочесть данную настройку полученным ранее. Для проверки корректности настройки построим переходный процесс по возмущению и оценим показатель качества. Переходный процесс по λ изображен на рисунке 5.12.
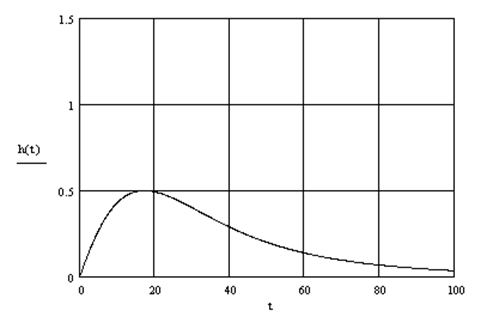
Рисунок 5.12 – Переходный процесс по λ
в контуре t
с ПИД- регулятором и с демпфированием
Видим, что по данному каналу система обладает значительно меньшим быстродействием, чем по каналу управления. Это закономерно, поскольку из передаточной функции объекта следует, что по этому каналу он является более инерционным. Численное значение критерия (5.16) равно I2
= 7.549.
 Итак, окончательно останавливаем свой выбор на ПИД- законе регулирования с демпфированием выходного сигнала регулятора и с настройками, определенными ранее. Итак, окончательно останавливаем свой выбор на ПИД- законе регулирования с демпфированием выходного сигнала регулятора и с настройками, определенными ранее.
6  ВЫБОР ТЕХНИЧЕСКИХ СРЕДСТВ ВЫБОР ТЕХНИЧЕСКИХ СРЕДСТВ
Большинство из технических средств, применяемых в нашей системе в контурах регулирования, уже описаны в предыдущих разделах. Систематизируем эти сведения и опишем средства, используемые для контроля и регистрации двух регулируемых и двух контролируемых величин.
Для измерения и регистрации величины pBr
в аппарате используются: датчик погружной типа ДПг-4М, нормирующий преобразователь типа П-201 и автоматический самопишущий мост типа КСУ-1М. Для регулирования величины pBr
используется электрический аналоговый регулятор Р17, реализующий ПИ- закон регулирования с демпфированием выходного сигнала.
Для измерения и регистрации температуры в аппарате используются: термопреобразователь сопротивления типа ТСП-0879-01 со статической характеристикой 50П и автоматический самопишущий мост типа КСМ-4. Для регулирования температуры в аппарате используется аналоговый регулятор Р17.2, реализующий ПИД- закон регулирования с демпфированием выходного сигнала.
Для измерения и регистрации величины pH
в аппарате используются: датчик ДПг-4М с электродной системой, настроенной на измерение pH
, вторичный прибор П-201 и автоматический самопишущий мост типа КСУ-1М.
Для измерения и контроля температуры в тепловой рубашке аппарата используются: термопреобразователь сопротивления типа ТСП-0879-01 со статической характеристикой 50П и автоматический самопишущий мост типа КСМ-4.
Рассчитаем надежность контура регулирования величины pBr
в аппарате. Под надежностью будем понимать вероятность безотказной работы всех звеньев контура в течение 1000 часов. В качестве характеристики надежности для каждого звена примем интенсивность отказов λ
. Данные для расчета: λ
ДПг
= 73·
10-6
1/ч; λП-201
= 35·
10-6
1/ч; λР17
= 54·
10-6
1/ч. Вероятность безотказной работы в течение t
часов контура, состоящего из n
элементов, вычисляется по формуле:
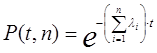 . (6.1) . (6.1)
Выполнив вычисления по этой формуле, получим P
(1000,3) = 0.85.
Найдем среднее время безотказной работы комплекта. Среднее время безотказной работы вычисляется по формуле:
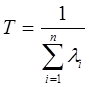 . (6.2) . (6.2)
 Выполнив вычисления по этой формуле, получим T
= 6172 ч. Выполнив вычисления по этой формуле, получим T
= 6172 ч.
Поскольку по требованиям стандартов вероятность безотказной работы допускается в пределах 0.85…0.99, то наш комплект удовлетворяет требованиям к надежности средств измерений.

ЗАКЛЮЧЕНИЕ
В данном курсовом проекте был исследован промышленный процесс получения фотографической эмульсии по двухструйной технологии. Была подробно исследована и смоделирована первая стадия этого процесса – приготовление и первое созревание эмульсии. На основе этого была разработана система автоматического управления процессом. Были обоснованы структура и параметры системы, а также оценено качество регулирования. В состав системы входят типовые элементы промышленной автоматики, выпускаемые отечественной промышленностью.
Следует отметить, что полученные результаты не являются абсолютно точными и адекватными. В ходе моделирования было сделано достаточно много упрощающих предположений, в особенности, на этапе линеаризации разгонных кривых. Строго говоря, объект является нелинейным (это показано в соответствующих разделах) и, как следствие, динамические процессы в нем зависят от предшествующего состояния системы. Проверка адекватности принятых нами упрощений может являться темой отдельной работы. Поэтому полученные нами результаты касательно настроек системы могут носить лишь рекомендательный характер.
С точки зрения структуры и состава входящих в нее средств автоматизации наша схема имеет промышленные аналоги (подобная система была применена в начале 90-х годов на Шосткинском ПО “Свема”). Система хорошо зарекомендовала себя и может считаться удачной.
 СПИСОК ЛИТЕРАТУРЫ СПИСОК ЛИТЕРАТУРЫ
1 Основы технологии светочувствительных материалов. Под ред. проф. Шеберстова. – М.: Химия, 1977. – 504 с.
2 Крамерс Х., Вестертерп К. Химические реакторы. – М.: Химия, 1967. – 264 с.
3 Теплотехника: Учебник / И.Т. Швец, В.И. Толубинский и др. – Киев: Вища школа, 1976. – 520 с.
4 Наладка автоматических систем и устройств управления технологическими процессами: Справочное пособие / А.С. Клюев и др. – М.: Энергоатомиздат, 1983. – 376 с.
ПРИЛОЖЕНИЕ А
Текст программы аппроксимации
Program approximation;
uses crt;const n=5;l=15; {n=числу полиномиальных коэффициентов}
{l=числу исходных точек неизвестной функции y}
type tarr1=array[1..n] of real;
tarr2=array[1..n,1..n] of real;
tarrl=array[1..l] of real;
tarr=array[0..n-1] of real;
var a:tarr2;
b:tarr1;
p:tarr;
f,x,y:tarrl;
i,j,k,d:integer;
v:tarr1;
xv,z:real;
h:string[1];
fil:text;
function g(t:tarr;x1:real):real;
var i2:integer;
w1:real;
begin
w1:=0;
for i2:=0 to n-1 do begin
w1:=w1+t[i2]*exp(i2*ln(x1));
end;
g:=w1;
end;
function max(t1:tarrl):real;
var i3:integer;
w:real;
begin
w:=t1[1];
for i3:=2 to l do
if t1[i3] > w then w:=t1[i3];
max:=w;
end;
procedure writing(c1:tarr2;c2:tarr1);
var i4,j4:integer;
begin
for i4:=1 to n do begin
for j4:=1 to n do
write(' ',c1[i4,j4]:10:3,' ');
write(' | ',c2[i4]:4:4);
writeln;
end;
end;
{=======Основной блок=========}
Begin
{абсциссы точек}
x[1]:=0.1;x[2]:=1;x[3]:=3;x[4]:=5;x[5]:=10;x[6]:=15;x[7]:=20;x[8]:=25;
x[9]:=30;x[10]:=35;x[11]:=40;x[12]:=50;x[13]:=60;x[14]:=80;x[15]:=100;
{ординаты - табличные значения}
y[1]:=0;y[2]:=0.2;y[3]:=1;y[4]:=2;y[5]:=5.5;y[6]:=9;y[7]:=12;y[8]:=14.3;
y[9]:=16;y[10]:=17.2;y[11]:=18.1;y[12]:=19;y[13]:=19.5;y[14]:=19.8;y[15]:=20;
z:=0;
{заполняем матрицы коэффициентов для системы}
for i:=1 to n do begin
for j:=1 to n do begin
for d:=1 to l do
z:=z+exp((i+j-2)*ln(x[d]));
a[i,j]:=z;z:=0;
end;
for d:=1 to l do
z:=z+y[d]*exp((i-1)*ln(x[d]));
b[i]:=z;z:=0;
end;
clrscr;
writeln('расширенная матрица системы :');
writing(a,b);
i:=1;
{решаем систему методом Гаусса. v - вектор неизвестных}
repeat
b[i]:=b[i]/a[i,i];
for j:=n downto i do
a[i,j]:=a[i,j]/a[i,i];
for k:=i+1 to n do begin
b[k]:=b[k]-b[i]*a[k,i];
for j:=n downto i do
a[k,j]:=a[k,j]-(a[i,j]*a[k,i]);
end;
i:=i+1;
until i=n+1;
v[n]:=b[n];
for i:=n-1 downto 1 do begin
v[i]:=b[i];
for j:=i+1 to n do
v[i]:=v[i]-(v[j]*a[i,j]);
end;
for i:=1 to n do p[i-1]:=v[i];
writeln;
writeln('эквивалентная ступенчатая матрица системы:');
writing(a,b);
writeln(' РЕШЕНИЕ : ');
for d:=0 to n-1 do writeln(p[d]:12:10);
writeln('значения аппроксимирующего полинома в узловых точках равны: ');
for d:=1 to l do begin
f[d]:=abs((g(p,x[d])-y[d])/{y[d]}6);
write(' ',g(p,x[d]):4:2,' ');
end;
writeln;
writeln('приведенная ошибка аппроксимации в % равна:');
writeln(max(f)*100:4:0,'%');
{=====запись в файл=====}
assign(fil,'result.txt');
rewrite(fil);
for d:=0 to n-1 do
writeln (fil,p[d]);
End.
|