Курсовая работа: Структурный синтез перестраиваемых arc-схем.

Содержание

1. Обобщенная структура перестраиваемых ARC-схем

2. Динамический диапазон перестраиваемых ARC-схем

3. Частотные свойства перестраиваемых ARC-схем

4. Процедура синтеза интеграторных структур

Библиографический список

1. Обобщенная структура перестраиваемых ARC-схем

Для снижения влияния электронных ключей на характеристики и параметры устройства целесообразно в качестве базисных структур использовать интеграторы (S_i (p)), что в общем случае с переменной постоянной времени (t_i ), и усилители (K_j (p)) с управляемым коэффициентом передачи (K_j ). Эти блоки объединяются в структуры посредством коммутирующей части схемы (КЧС), которая также связывает их с источником сигнала x₀ и входным узлом схем y₀ (рис. 1).

Рассматриваемая модель перестраиваемого устройства описывается следующей матрично-векторной системой уравнений:

(1)

Смысл векторов X_S , X_K , Y_S , Y_K , поясняется векторным сигнальным графом, изображенным на рис. 1. Структура матриц B_SS , B_SK , B_KS , B_KK и векторов T_K , T_S , A_K , A_S , относящихся к КЧС, приведена в табл. 1, где знак Т означает транспонирование.

Из векторного графа следует, что данная модель состоит из трех основных частей. Первая часть (компоненты векторов A_K и A_S ) является расщепителем, который посредством разветвления преобразует скалярную величину входного сигнала x ₀ в векторную, воздействующую на соответствующие входы базисных структур. Вторая и наиболее важная часть системы (компоненты всех матриц, входящих в (2)) осуществляет основную операцию над векторными сигналами X_S и X_K , преобразуя их в Y_s , Y_K . Здесь сосредоточены физически осуществимые принципы формирования коэффициентов полинома знаменателя передаточной функции и заложены основы конструирования коэффициентов полинома числителя. Третья часть (компоненты векторов T_S , T_K и скаляр t₀ ) реализует сумматор, обеспечивающий связь с выходами базисных структур.

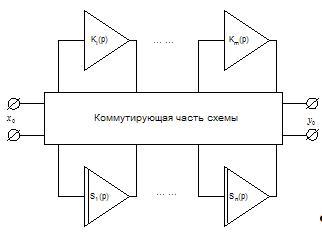
Рис. 1. Обобщенная структура перестраиваемого ARC-устройства

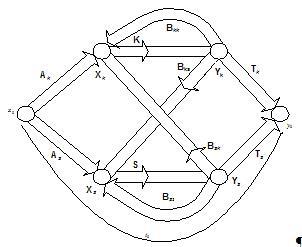
Рис. 2. Векторный сигнальный граф обобщенной структуры

Таблица 1

Компоненты коммутирующей части схемы

Для обеспечения пассивности КЧС необходимо выполнить условия

(2)

(3)

(4)

гарантирующие возможность ее построения на базе резисторов, причем для любого h-го усилителя с фиксированным коэффициентом передачи возможна реализация отрицательных передач путем использования неинвертирующего входа операционного усилителя (ОУ). В этом случае в неравенстве (2) учитываются модули соответствующих величин. Базисные структуры описываются диагональными матрицами

(5)

компоненты которых являются передаточными функциями реальных интеграторов и усилителей, поэтому

(6)

(7)

где – площадь и статический коэффициент усиления ОУ, положенного в основу i-го интегратора (j-го усилителя); – коэффициент передачи на холостом ходу i-го (j-го) резисторного управителя.

Передаточная функция обобщенной структуры следует из системы векторно-матричных уравнений (1) и при переходе к блочным (клеточным) матрицам и векторам имеет вид:

. (8)

Для идеальных ОУ блочная матрица основной части системы может быть представлена следующим образом:

. (9)

При решении конкретных задач качественного характера удобным оказывается представление

(10)

при этом векторы , компоненты которых являются передаточными функциями на выходах интегрирующих и масштабных усилителей, определятся после обращения матрицы L_и по формулам Фробениуса [1] из следующих соотношений:

(11)

где .

Воспользовавшись методом В.Н. Фаддеевой [6] для вычисления резольвенты матрицы , функцию (10) можно привести к дробно-рациональному виду

(12)

где коэффициенты числителя и знаменателя определяются алгоритмом:

(13)

Здесь 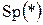– след (сумма диагональных элементов) соответствую-щей матрицы.

Приведенный алгоритм позволяет на последнем шаге q = n осуществить контроль результата, т.к. . Однако он довольно чувствителен к ошибкам округления, поэтому при численных методах решения задачи необходимо предусмотреть перевод компонент матриц в числа с удвоенной точностью.

2. Динамический диапазон перестраиваемых ARC-схем

Верхняя граница динамического диапазона определяется не только максимальным выходным напряжением ОУ при заданном коэффициенте нелинейных искажений, но и свойствами схемы. В общем случае на выходах ОУ в рабочем диапазоне частот W напряжения могут превышать выходное напряжение схемы, определяемое входным сигналом и максимальным коэффициентом передачи . Поэтому их уровень должен определяться соотношением

(14)

где

Собственный шум схемы, состоящей из интеграторов и масштабных усилителей, и, следовательно, нижняя граница ее динамического диапазона определяются шумами активных элементов и резисторов. Как правило, шум резисторов можно уменьшить на этапе расчета или параметрической оптимизации схемы соответствующим выбором не только их типов, но и номиналов, поэтому на этапе синтеза можно учитывать только влияние шумов ОУ. В этом случае

(15)

, (16)

где , – комплексный коэффициент передачи с выхода i-го (j-го) ОУ к нагрузке; , – эквивалентная спектральная плотность мощности источников шумовой модели i-го (j-го) ОУ; – границы диапазона рабочих частот W.

Таким образом, мерой динамического диапазона схемы для идентичных ОУ является произведение

(17)

которое в процессе синтеза необходимо минимизировать в диапазоне частот W или, если это возможно (например, для узкополосных устройств и звеньев второго порядка), в некоторой особой точке .

Учет влияния параметров активных элементов на обобщенную структуру производится через матрицу

(18)

вытекающую из системы (1).

Воспользовавшись методом пополнения [87] при обращении этой матрицы, можно установить, что чувствительность

динамический диапазон частотный интеграторный

(19)

определяет влияние i-го (j-го) ОУ на верхний и нижний уровни динамического диапазона схемы, причем следуют из соотношений (8) при

(20)

(21)

и являются передаточными функциями системы при подаче сигнала на неинвертирующие входы ингеграторов и масштабных усилителей.

Передаточные функции на выходе i-го интегратора F_st (р) и j-го масштабного усилителя F_kj (р) являются компонентами векторов F_s и F_k и, следовательно, определяются из (8), когда

(22)

или

. (23)

Для вычисления полиноминальных коэффициентов H_i (p), H_j (p), F_si (p), F_kj (p) можно воспользоваться алгоритмом (13) с учетом приведенных выше соотношений.

Таким образом, как это следует из (19), (17) и (14), уменьшение влияния i-го (j-го) ОУ на нижний уровень динамического диапазона без изменения его верхней границы возможно либо уменьшением модуля чувствительности передаточной функции при условии, что максимальное входное напряжение на его входе не меньше максимального напряжения в других узлах схемы, т.е. когда

(24)

либо увеличением этого отношения до уровня при неизменной чувствительности.

3. Частотные свойства перестраиваемых ARC -схем

Площади усиления ОУ, входящих в состав интеграторов и масштабных усилителей, не только изменяют коэффициенты передаточной функции, но и повышают ее порядок, что в свою очередь искажает ожидаемые характеристики устройства. Для учета этого эффекта воспользуемся (m+n) раз методом пополнения для обращения матрицы (18). В этом случае

(25)

не содержит составляющих, обратно пропорциональных произведениям площадей усиления ОУ, влияние которых на частотные характеристики, как правило, мало.

Тогда

(26)

(27)

где L_i (р), L_j (p) являются передаточными функциями системы на выходе i-го, j-ro ОУ при передаче сигнала на выход i-го интегратора или j-ro масштабного усилителя через компоненты векторов (20) и (21). Вычисление этих функций производится по соотношениям (8) – (11) и алгоритму (13) при

(28)

(29)

Таким образом, для получения поправочных полиномов числителя и знаменателя достаточно знать набор локальных передач L_i (p), L_j (p), H_i (p), F_si (p), F_kj (p) устройства, которые являются необходимыми для полного анализа схемы.

4. Процедура синтеза интеграторных структур

Аналогично поиску структур ARC-cxeм с фиксированными параметрами построение интеграторных схем базируется на соотношениях (2) – (4) и сводится к выбору компонент матриц В _ss , В _ks , B _sk , В _kk , векторов T _s , T _k , A _s , A _k . В п. 1 отмечалось, что матрицы B _ks , B _sk , B _kk отображают функциональные связи, характерные для сумматоров и устройств масштабирования. Если предположить возможность реализации этих устройств в виде идеализированных блоков с произвольным численным значением локальных передач, то, как это видно из (1)

С => B _ss ; р{} = sI _n ; А _k = 0; Т _k = 0, (30)

что приводит к описанию структуры по методу пространства состояний [2], в рамках которого применима процедура непосредственного интегрирования. Настоящий предельный переход позволяет существенно упростить процедуру синтеза идеализированных структур как с фиксированными, так и переменными параметрами. Продемонстрируем простейший алгоритм построения идеализированной принципиальной схемы.

На рис. 3 показана структура звена второго порядка, следующая из метода непосредственного интегрирования.

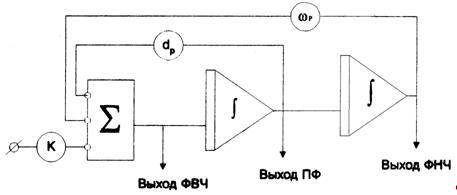
Рис. 3. Исходная структура звена второго порядка

На первом этапе сумматоры заменяются их реализациями на операционных усилителях с произвольными локальными коэффициентами передачи, а на втором осуществляется замена интегрирующих блоков на интеграторы либо с фиксированными, либо с управляемыми параметрами. В этом случае компоненты матрицы С могут принимать любые наперед заданные значения. Из принципиальных схем базисных структур видно, что полученная в результате таких преобразований схема будет иметь большее число степеней свободы и, следовательно, позволит без дополнительных активных элементов образовать в рамках предложенного принципа собственной компенсации контуры обратных связей. Принципиальная схема такого звена показана на рис. 4.

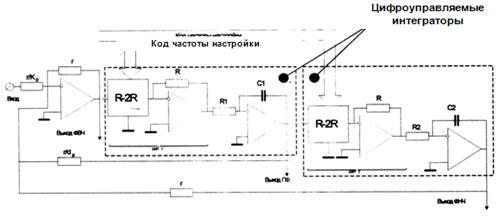
Рис. 4. Универсальное звено второго порядка

с масштабной перестройкой

Поясним процедуру поиска этих контуров на конкретном примере. В схемотехнике перестраиваемых ARC-устройств частотной селекции осо-бое место занимают звенья второго порядка, являющиеся основой не только каскадных, но и многопетлевых реализаций [2]. Если для звеньев второго порядка характеристический полином

(31)

под действием площади усиления получит абсолютное приращение

(32)

то относительные изменения частоты и затухания полюса будут иметь вид

(33)

Тогда для компенсации влияния коэффициентов на параметры схемы необходимо, чтобы контуры вводимых обратных связей характеризовались возвратными отношениями

(34)

или

(35)

где n и m – количество интеграторов и масштабных усилителей в схеме, – коэффициенты, принимающие в процессе проектирования различные значения.

Для вычисления коэффициентов, входящих в (34) и (35), осуществляется их сопоставление с , после чего в каждом конкретном случае может быть определен необходимый вид передаточной функции, реализуемой на выходах интеграторов и масштабных усилителей со специально созданных входов схемы. Вытекающие из (34) и (35) функ-циональные признаки и правила построения схем приведены в табл. 2. Приведенные во второй части табл. 3 варианты компенсации относительного изменения затухания полюса за счет изменения коэффициента не противоречат принципу расширения динамического диапазона. Для любого i-го (j-го) ОУ

(36)

При одновременной компенсации изменений и d_p в качестве функционального признака используется одна из возможных сумм передаточных функций. Если существует свобода выбора, то целесообразно использовать выходы тех ОУ, чувствительность к площади усиления которых больше, и, следовательно, в этом случае ( является особой точкой) чувствительность

(37)

уменьшается, что и снижает уровень собственного шума.

Здесь являются слагаемыми , обусловленными действием площади усиления i-го (j-го) ОУ.

Приведенные результаты показывают, что снижение чувствительности для каждого i-го (j-го) ОУ зависит от возможности реализации на его выходе нужной передаточной функции, которая после замыкания компенсирующего контура обратной связи, образованного соединением входа ОУ со специально созданным входом схемы, обеспечивает собственную компенсацию влияния частотных свойств активных элементов. В этом случае

(38)

и коэффициенты результирующего поправочного полинома могут принимать достаточно малые значения. Как видно из соотношения (38), благодаря чередованию знаков в слагаемых, определяющих , возможна минимизация их численных значений. Это обеспечивает их взаимную компенсацию и способствует расширению диапазона рабочих частот без увеличения эквивалентной спектральной плотности шума схемы.

Таблица 2

Топологические правила построения схем

Таблица 3

Основные этапы проектирования

Для замыкания компенсирующих контуров обратных связей может оказаться необходимым применение активных сумматоров, реализованных на N ОУ. Их влияние на характеристический полином (31) находится из соотношения

(39)

Следовательно, возникающие дополнительные изменения частоты и затухания полюса

(40)

достаточно малы и определяются реализуемым d_p . Здесь является глубиной отрицательной обратной связи в l-м ОУ.

Полученные соотношения, топологические правила и выводы совместно с ранее рассмотренным алгоритмом позволяют существенно формализовать процедуру поиска малошумящих звеньев с активной компенсацией.

Рассмотрим построение на основе изложенного материала универсального звена второго порядка с расширенным частотным и динамическим диапазонами. Будем считать, что на втором этапе получена схема, приведенная на рис. 5 (ветвь , показанная пунктиром и связывающая инвертирующий вход ОУ1 с неинвертирующим входом ОУ2, отсутствует, а узел q заземлен). Эта схема следует из рис. 4. Указанные в схеме соотношения элементов не влияют на результаты и приняты для упрощения вида промежуточных соотношений. Результаты различных этапов синтеза приведены в табл. 3.

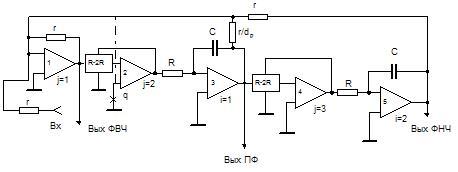
Рис. 5. Универсальное звено с масштабной перестройкой

На первом этапе по информации, приведенной в табл. 3, составлены матрицы и векторы схемы, причем входная цепь первого масштабного усилителя (j=l) заменена резистивной звездой, образующей пассивный сумматор, коэффициент передачи которого при d_p < l равен 0,5. Коэффициенты передаточной функции идеализированной схемы определены по алгоритму (13).

На втором этапе найдены коэффициенты поправочного полинома (32) и относительные изменения параметров, учитывающие влияние частотных свойств ОУ на передаточную функцию и характеристики для максимальной частоты полюса (). При этих же условиях вычислены модули комплексных коэффициентов передачи со входа каждого ОУ на выход ФНЧ схемы , определяющие максимальную спектральную плотность шума

(41)

где – спектральная плотность шума ОУ.

Так как в рассматриваемой схеме всплесков коэффициентов передачи во внутренних узлах не наблюдается (), то в данном случае для всех ОУ чувствительность (37) определяет качественные показатели устройства. Анализируя полученные результаты, можно выделить ОУ1, наиболее сильно влияющий на частотный и динамический диапазоны схемы.

На третьем этапе в соответствии с алгоритмом синтеза реализована собственная компенсация влияния ОУ1. Согласно правилам, приведенным в табл. 2, и соотношению (38), для решения этой задачи необходимо определить такой узел схемы q, для которого на выходе ОУ1 реализуется функция ФВЧ или ФНЧ. В общем случае это определяется через алгоритм (13), так как составляющие резольвенты основной матрицы вычислены на предыдущих этапах. Так, при подаче сигнала на неинвертирующий вход ОУ2 является функцией ФНЧ, поэтому замыканием инвертирующего входа ОУ1 и неинвертирующего входа ОУ2 (связь , показанная на рис. 5 пунктиром) обеспечивается снижение модуля соответствующей чувствительности и расширение не только частотного, но и динамического диапазона. Численные значения параметров, подтверждающие результат, приведены в последней части табл. 3.

В полученной схеме идеализированные параметры исходного варианта не изменяются, так как при идеальных ОУ сигнал на инвертирующем входе ОУ1 отсутствует, и компенсирующая связь не действует.

Для реальных ОУ в области достаточно высоких частот участок цепи от неинвертирующего входа ОУ2 до инвертирующего входа ОУ1 за счет напряжения рассогласования на входе ОУ1 вырабатывает такой сигнал обратной связи, который уменьшает изменения параметров устройства. Аналогично введенный контур действует и на собственный шум схемы, возникающий за счет ОУ1. Это объясняется тем, что коэффициенты передачи энергии шума от входа ОУ2 на выход ФНЧ имеют разные значения.

Четырехкратное применение настоящей процедуры позволяет получить принципиальную схему универсального звена (рис. 6) с масштабной перестройкой. При идеальных ОУ основные параметры звена определяются следующими соотношениями:

(42)

где – эквивалентные постоянные времени цифроуправляемых интеграторов; – коэффициент передачи ЦАП; – коэффициент сдвига частоты полюса.

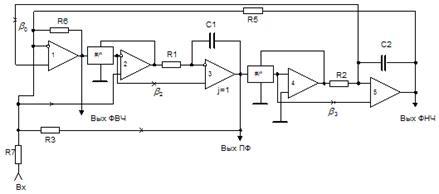
Рис. Упрощенная принципиальная схема универсального звена

с расширенным частотным и динамическим диапазонами

Влияние площади усиления ОУ на частоту и затухание полюса описывается относительными изменениями

(43)

(44)

где .

Логические переменные устанавливают связи между инвертирующими и неинвертирующими входами ОУ и демонстрируют эффективность действия каждого из компенсирующих контуров.

Библиографический список

1. Блажкевич, Б.И. Топологический метод поиска минимальных структур RLC-цепей [Текст] / Б.И. Блажкевич, Е.Д. Михайлова // Теоретическая электротехника. – 2009. – Вып. 14. – С. 14–19.

2. Блажкевич, Б.И. Физические основы алгоритмов анализа электронных цепей [Текст] / Б.И. Блажкевич. – Киев : Наукова думка, 2009. – 240 с.

3. Богатырев, В.Н. Проектирование и разработка ОУ на основе КМОП КНИ технологии [Текст] / В.Н. Богатырев [и др.] // Проблемы разработки перспективных микроэлектронных систем : материалы Всерос. науч.-техн. конф. – Подмосковье, 2009. – С. 290–297.

4. Бунза, Дж. Основные направления развития автоматизации проектирования в 1990-х годах [Текст] / Дж. Бунза, Г. Хоффман, Эд. Томсон // Электроника. – 2010. – № 2. – С. 39–47.

5. Виляев, Л.Ю. Аналого-цифровой БМК «Рапира» и библиотека функциональных элементов на его основе [Текст] / Л.Ю. Виляев, Ю.Н. Владимиров, В.В. Полевиков, И.Н. Шагурин // Актуальные проблемы микроэлектроники и твердотельной электроники : труды IV Всерос. НТК с междунар. участием. – 2007. – С. 123–124.

6. Гадахабадзе, Н.Г. Оптимальное проектирование электронных схем методом -преобразований [Текст] / Н.Г. Гадахабадзе, Н.К. Джибладзе, В.К. Чичинадзе // Автоматика и телемеханика. – 2007. – № 4. – С. 86–94.

7. Гантмахер, Ф.Р. Теория матриц [Текст] / Ф.Р. Гантмахер. – М. : Наука, 2006. – 576 с.

8. Гехер, К. Теория чувствительности и допусков электронных цепей [Текст] / К. Гехер. – М. : Сов. радио, 2010. – 315 с.

9. Гудинаф, Ф. Интегральные программируемые фильтры, программируемые напряжением [Текст] / Ф. Гудинаф // Электроника. – 2010. – № 5. – С. 14–17.

10. Гудинаф, Ф. Новая технология производства высокочастотных линейных ИС [Текст] / Ф. Гудинаф // Электроника. – 2008. – № 7–8.

11. Гудинаф, Ф. Новое поколение низковольтных аналоговых ИС – у порога рынка [Текст] / Ф. Гудинаф // Электроника. – 2009. – № 5. – С. 8–18.

12. Гутников, В.С. Интегральная электроника в измерительных устройствах [Текст] / В.С. Гутников. – Л. : Энергия, 2010. – 248 с.

13. Зааль, Р. Справочник по расчету фильтров [Текст] / Р. Зааль ; пер. с нем. под ред. Н. Слепова. – М. : Сов. радио, 2007. – 752 с.

14. Знаменский, А.Е. Активные RC-фильтры [Текст] / А.Е. Знаменский, И.Н. Теплюк. – М. : Связь, 2008. – 279 с.

15. Иванов, Ю.И. Увеличение гарантированного затухания в полосе задерживания RC-фильтров второго порядка [Текст] / Ю.И. Иванов // Проблемы современной аналоговой микросхемотехники : сборник трудов МНПС. – Шахты, 2009. – С. 95–101.

16. Ильин, В.Н. Интеллектуализация САПР [Текст] / В.Н. Ильин // Известия вузов. Радиоэлектроника.– 2007. – Т. 30, № 6. – С. 5–13.

17. Капустян, В.И. Оптимизация структур активных фильтров высокого порядка [Текст] / В.И. Капустян, С.А. Букашкин, В.С. Денисов // Радиотехника. – 2008. – № 8. – С. 51–53.

18. Капустян, В.И. Проектирование активных фильтров высокого порядка [Текст] / В.И. Капустян. – М. : Радио и связь, 2006. – 160 с.

19. Каталог разработок Российско-Белорусского центра аналоговой микросхемотехники [Текст] / под ред. С.Г. Крутчинского. – Шахты : Изд-во ЮРГУЭС, 2006. – С. 96.

20. Квакернаак, Х. Линейные оптимальные системы управления [Текст] : пер. с англ. / Х. Квакернаак, Р. Сиван. – М. : Мир, 2007. – 650 с.

21. Коротков, А.С. Микроэлектронные аналоговые фильтры на преобразователях импеданса [Текст] / А.С. Коротков. – СПб. : Наука, 2009.