Содержание
1. Модель войны или сражения. 2
2. Модель Мальтуса. 4
3. Система хищник-жертва. 8
4. Построение фракталов. 11
4.1. Треугольник Серпинского. 11
4.2. Построение множества «Папоротник». 12
1. Модель войны или сражения
Противостояние двух противников, например двух армий, может быть описано с помощью модели Ланкастера. В ней состояние системы описывается точкой (x,y)
положительного квадранта плоскости. Координаты этой точки, x
и y
— это численности противостоящих армий. Модель описывается с помощью системы уравнений:
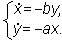
Здесь a
— мощность оружия армии x,
а b
— армии y
. Здесь предполагается, что каждый солдат армии x
убивает за единицу времени a
солдат армии y
и каждый солдат армии y
убивает b
солдат армии x
. Точка над буквой здесь и далее означает производную по времени t
, то есть скорость изменения обозначенной буквой величины.
Это жесткая модель, которая допускает точное решение
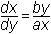
 , где с
– некоторая константа.
Последнее уравнение имеет несколько вариаций. Для исследования предложенной модели будем использовать запись  , варьируя мощности оружия армий xи y с помощью параметра с
.
Для исследования модели будем использовать возможности системы компьютерной математики Maxima.
В системе Maxima есть встроенная функция для построения графиков
функций, заданных неявно. Ее синтаксис:
implicit_plot (expr, x_range, y_range)
implicit_plot ([expr_1, ..., expr_n], x_range, y_range)
где expr – уравнение, задающее неявную функцию, x_range и y_range – промежутки изменения переменных x и y.
Для того, чтобы можно было использовать функцию implicit_plot, необходимо подключить пакет, содержащий эту функцию, с помощью команды load(implicit_plot).
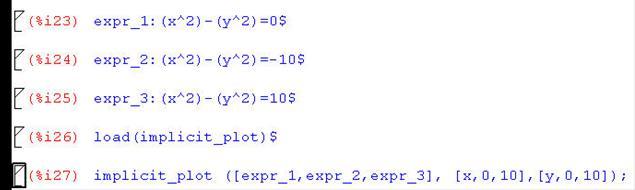
Листинг 1
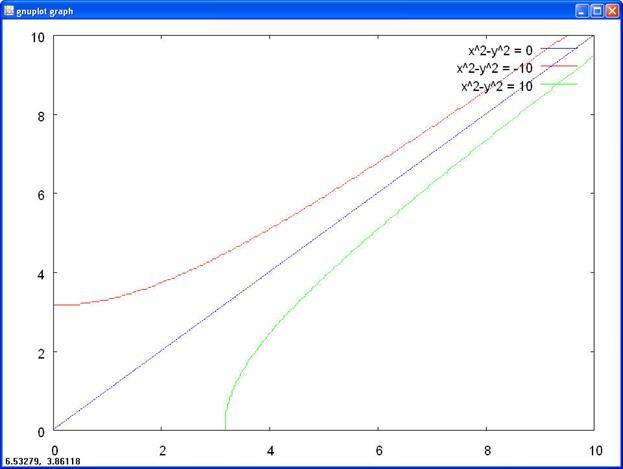
Рисунок 1 Модель войны (сражения)
Эволюция численностей армий x
и y
происходит вдоль гиперболы, заданной этим уравнением (рис. 1). По какой именно гиперболе пойдет война, зависит от начальной точки.
Эти гиперболы разделены прямой, которой соответствует значения параметра с =0.
Если начальная точка лежит выше этой прямой (случай с < 0
на рис. 1), то гипербола выходит на ось y
. Это значит, что в ходе войны численность армии x
уменьшается до нуля (за конечное время). Армия y
выигрывает, противник уничтожен.
Если начальная точка лежит ниже (случай с > 0
), то выигрывает армия x
. В разделяющем эти случаи состоянии (на прямой) война заканчивается ко всеобщему удовлетворению истреблением обеих армий. Но на это требуется бесконечно большое время: конфликт продолжает тлеть, когда оба противника уже обессилены.
Вывод
:
для борьбы с вдвое более многочисленным противником нужно в четыре раза более мощное оружие, с втрое более многочисленным — в девять раз и т. д. (на это указывают квадратные корни в уравнении прямой).
На самом деле простейшая модель дает даже полезное количественное предсказание: наклон разделяющей нейтральной прямой в нуле определяется формулой 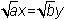 , где a
и b
— значения коэффициентов в нуле, соответствует случаю с = 0.
То есть принцип «если противников вдвое больше, то надо иметь в четыре раза более мощное оружие» справедлив на конечном этапе взаимного истребления, в то время как на начальном этапе войны число 4 нужно откорректировать (учитывая вид коэффициентов a
и b
).
2. Модель Мальтуса
Скорость роста пропорциональна текущему размеру популяции. Она описывается дифференциальным уравнением
 ,
где k
— некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решением этого уравнения является экспоненциальная функция  . Если рождаемость превосходит смертность (k
> 0), размер популяции неограниченно и очень быстро возрастает. Понятно, что в действительности этого не может происходить из-за ограниченности ресурсов. При достижении некоторого критического объёма популяции модель перестает быть адекватной, поскольку не учитывает ограниченность ресурсов.
Для исследования модели будем использовать возможности системы компьютерной математики Maxima. Меняем значение параметра k
, строим графики:
1) к=0.2;
Листинг 2
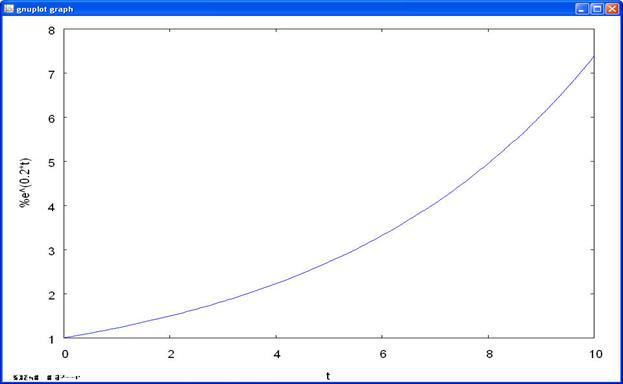
Рисунок 2 Модель Мальтуса (к=0.2)
2) к=2;
Листинг 3
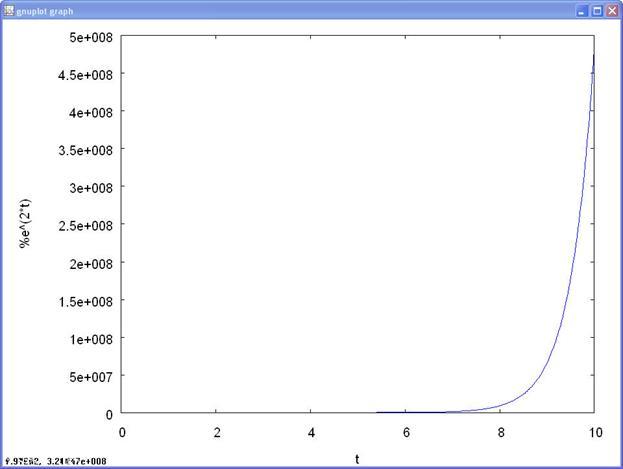
Рисунок 2 Модель Мальтуса (к=2)
3) к=15;
Листинг 4
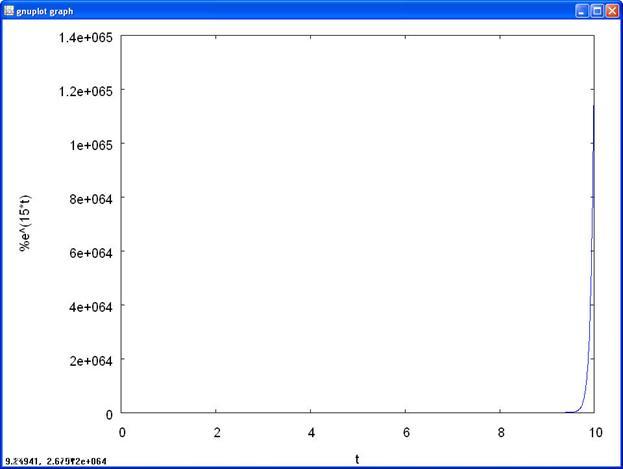
Рисунок 4 Модель Мальтуса (к=15)
Вывод: если рождаемость превосходит смертность (k
> 0), размер популяции неограниченно и очень быстро возрастает.
3. Система хищник-жертва
Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов x
, число лис y
. Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Вольтерра — Лотки:
где x– число жертв, у – число хищников,  – прирост жертв
a>0, b>0,
где a
– скорость размножения жертв в отсутствие хищников, -
by
– потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи (x=0)
относительная скорость изменения популяции хищников равна  , c >
0, наличие пищи компенсирует убывание.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки.
Для исследования модели будем использовать возможности системы компьютерной математики Maxima. Рассмотрены два случай:
1. Первоначальное соотношение лисы/кролики 3/7;
2. Первоначальное соотношение лисы/кролики 7/3;
Построены фазовые портреты системы, в трехмерном и двумерном пространстве координат, при a
= 4,
b
= 2.5,
c
=2,
d
= 1.
Листинг 5
Рисунок 5 Система хищник-жертва, фазовый портрет 3d
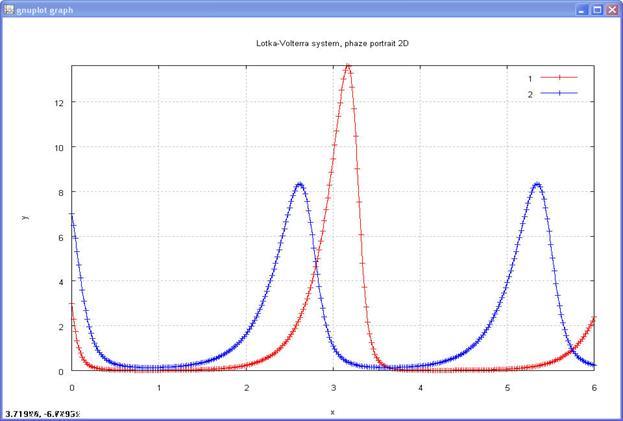
Рисунок 6 Система хищник-жертва, фазовый портрет 2d
Вывод: рассмотренный процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов, обе популяции сначала растут. Когда число хищников достигает определенной величины, популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает предельной величины, число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Происходит сокращение популяций. С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и процесс повторяется снова и снова. На графике четко виден периодический характер процесса. Периодичность процесса явственно видна на фазовой плоскости — фазовая кривая — замкнутая линия. Самая левая точка, этой кривой, — это точка, в которой число жертв достигает наименьшего значения. Самая правая точка — точка пика популяции жертв. Между этими точками количество хищников сначала убывает, до нижней точки фазовой кривой, где достигает наименьшего значения, а затем растет до верхней точки фазовой кривой.
|
