Зміст
Вступ
Питання 1. Теорія активного комплексу (перехідного стану)
Питання 2. Реакції, що протікають в адсорбційній області
Задача 3
Задача 4
Задача 5
Задача 6
Висновок
Список літератури
Контрольна робота з дисципліни "Кінетика і каталіз у ТНР".
Хімічна кінетика, що є розділом фізичної хімії, містить у собі, як окремий випадок, каталіз. Усі проблеми каталізу (включаючи і питання вибору каталізаторів) зводяться до основних проблем хімічної кінетики, тобто до встановлення елементарних хімічних процесів, з яких складається весь процес у цілому, і встановлення закону, по якому протікає процес у часі. Через велику практичну важливість каталітичних процесів, стало прийнятим виділяти цей розділ з хімічної кінетики.
Знання механізму процесу дозволяє описати швидкість хімічної реакції відповідним математичним рівнянням, на основі якого можна зробити кореляцію дослідних даних і їхню екстраполяцію за межі експериментально вивченого інтервалу робочих умов.
Теорія активного комплексу або теорія перехідного стану розроблена Е. Вінгером, М. Поляні, Г. Ейрінгом і М. Евансом у 30-х роках 20-го століття. Ця теорія дозволяє розрахувати швидкість, не застосовуючі експериментальні дані визначення стеричного множника Р. Вона встановлює зв'язок між швидкістю хімічної реакції і структурою реагуючих речовин. Відповідно до неї швидкість реакції визначається не тільки зіткненням, а і наступним за ним процесом перегрупування атомів у молекулах. Цей стан характеризується ослабленими старими зв'язками і з'явившимися новими, ще не “зміцнілими" зв'язками. Він називається перехідним станом або активним комплексом.
Наприклад, для реакції H
2
+I
2
= 2HI
утворення перехідного комплексу можна схематично зобразити у вигляді:
 H I H…I* H – I H I H…I* H – I
   + +
H I H…I H – I (1)
Час "життя" активованого комплексу визначається значенням:
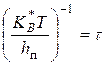 , (2) , (2)
де КВ
- постійна Больцмана;
h
п
- постійна Планка;
Т
- абсолютна температура.
Чисельне значення часу "життя" складає приблизно 10-13
секунд
. Незважаючи на це, активований комплекс вважають молекулою і тому в даній теорії зроблене допущення, що активний комплекс знаходиться в рівновазі з вихідними речовинами, що трохи суперечливо, але проте результати дає достовірні.
Відповідно до цієї теорії швидкість реакції розраховують по формулі:
 , (3) , (3)
де  - константа швидкості стадії активування, наприклад, - константа швидкості стадії активування, наприклад,
 
   H I H…I (4) H I H…I (4)
  + +
H I H…I
Е
= ΔН* -
зміна тепломісткості при утворенні активного комплексу. Вона збігається за змістом з енергією активації.
ΔS*
- зміна ентропії в тім же процесі (ентропія активації)
С
1
і С
2
-
концентрації вихідних речовин.
По суті справи:
 (5) (5)
де К
* - константа рівноваги активного комплексу.
Порівняння рівнянь для розрахунку швидкостей по теорії активних зіткнень і по теорії перехідного стану дає:
 (6) (6)
де Р
- стеричний множник;
Звідси стає ясним зміст Р
: при  і P
>1,
а при і P
>1,
а при  P
<1. При утворенні активного комплексу з двох молекул невпорядкованість повинна зменшуватися і тем сильніше, ніж складніший комплекс. У цьому випадку P
<1. При утворенні активного комплексу з двох молекул невпорядкованість повинна зменшуватися і тем сильніше, ніж складніший комплекс. У цьому випадку  .
Іншими словами процеси “творення”, для яких .
Іншими словами процеси “творення”, для яких  , протікають повільніше (P
<1), чим процеси руйнування, для яких , протікають повільніше (P
<1), чим процеси руйнування, для яких  . .
Однією з перших теорій, що відносяться до каталізу поверхнями твердих речовин, є теорія, запропонована в 1825 р. Фарадеєм; деякі її положення справедливі і в даний час. Відповідно до цієї теорії перша стадія являє собою адсорбцію реагентів; реакція протікає в адсорбційному шарі. Вважалося, що конденсація приводить до зближення молекул і більшому числу взаємних зіткнень і, отже, до більш високої швидкості реакції.
Однак є багато даних, що спростовують ці найпростіші представлення. Так, наприклад, найефективніші адсорбенти не завжди є і найбільш ефективними каталізаторами. Крім того, каталітична дія досить специфічна, тобто визначені реакції каталізуються тільки відповідними каталізаторами. Очевидно потрібно не тільки зближення реагуючих молекул. Згідно даним сучасної науки, адсорбція розглядається як умова, необхідна, але не достатня для протікання реакції на поверхні твердих каталізаторів.
Адсорбція обумовлена притяганням між молекулами поверхні твердого тіла (адсорбенту) і молекулами рідини або газу (адсорбата). Експериментально виявлені два типи адсорбції, у яких інтенсивність притягання відрізняється приблизно на порядок. У деяких випадках притягання порівняно невелике і має ту ж природу, що і притягання між будь-якими двома молекулами, тобто відбувається фізична адсорбція.
В інших випадках сили притягання близькі силам, що виявляються при утворенні хімічних зв'язків; такай процес називають хімічною адсорбцією,
або хемосорбцією.
Теплові ефекти.
Адсорбція є екзотермічним процесом. При фізичній адсорбції газів теплові ефекти мають приблизно той же порядок, що і теплоти конденсації, тобто декілька сот калорій на 1 моль.
При хемосорбції теплові ефекти по величині наближаються до теплових ефектів хімічних реакцій і складають 41 900 - 419 000 кдж /кмоль.
Так, наприклад, теплота адсорбції кисню на вуглеці дорівнює 335200 кдж/кмоль
(близько 80 ккал/моль),
а теплота згоряння вуглецю складає 393860 кдж/моль
(94 ккал/моль).
У цьому випадку дійсно утвориться стабільне з'єднання і при спробах видалити адсорбат з поверхні шляхом вакуумування разом з киснем виділяється деяка кількість окису вуглецю.
Вплив температури.
Важливо розрізняти кількість адсорбованої речовини і швидкість адсорбції. Оскільки і фізична і хімічна адсорбція - процеси екзотермічні, рівноважний зміст адсорбованої речовини завжди знижується при зростанні температури.
Фізична адсорбція протікає досить легко, тому рівноважний стан установлюється швидко навіть при низьких температурах. Хемосорбція зв'язана з енергією активації і швидкість процесу незначна, але істотно зростає з підвищенням температури; рівноважний стан також установлюється повільно.
Вплив тиску.
При фізичній адсорбції тиск впливає на рівновагу. При зниженні тиску система повертається у вихідний стан: процес цілком оборотний. З іншого боку, рівновага при хемосорбції майже не залежить від тиску. Мономолекулярний адсорбційний шар, що характерний для хемосорбції, утворюється навіть при дуже низьких тисках. Однак швидкість обох типів адсорбції зростає зі збільшенням тиску.
Вплив поверхні.
Для фізичної адсорбції має значення лише величина поверхні, але хімічна адсорбція - досить специфічний процес. Так, наприклад, водень хемосорбується не окисом алюмінію, а нікелем, і кисень не окисом магнію, а вуглецем. Таке поводження погоджується з припущенням, що хемосорбція подібна в загальному з хімічною реакцією. На хемосорбцію впливають фізичний стан поверхні і її хімічний склад. Неоднорідність поверхні каталізаторів доводиться, наприклад, тим, що теплота процесу поступово знижується в міру протікання хемосорбції. Поверхня складається з атомів різного ступеня насиченості. Атоми з країв кристалів, тріщин і виступів, імовірно, менш насичені і, отже, більш активні.
В даний час існує кілька теорій поверхневої активності. Відповідно до однієї з останніх теорій, активність поверхні обумовлена визначеними типами дефектів кристалічних ґрат. Збільшення активності каталізаторів під впливом невеликих кількостей добавок, які називаються промоторами, у деяких випадках задовільно пояснюється тим, що атоми промотору проникають у кристалічні ґрати каталізатора і викликають деформації і внутрішні напруження ґрат.
Зараз точно встановлено, що поверхня твердого тіла неоднорідна, а також, що хемосорбція і хімічна реакція протікають лише на визначених ділянках поверхні. Ці ділянки звичайно називають активними ділянками, активними центрами або активними точками.
Слід зазначити, що хемосорбція обмежена утворенням мономолекулярного шару і, таким чином, є однією зі стадій реакції на поверхні, оскільки валентні сили швидко убувають зі збільшенням відстані. Фізична адсорбція ніколи не обмежується мономолекулярним шаром.
Взагалі основні фактори, що визначають кінетику реакцій, можна сформулювати в такий спосіб:
- Адсорбція являє собою необхідну проміжну стадію каталітичних гетерогенних реакцій.
- Хемосорбція є тим типом адсорбції, що завжди супроводжує хімічні реакції на поверхні. Хемосорбція - характерна ознака гетерогенних каталітичних реакцій.
- Каталітичні поверхні неоднорідні і хемосорбція протікає переважно на активних ділянках поверхні.
Реакція 1-го порядку протікає на 30% при температурі 250
С
за 30 хвилин
, а при температурі 400
С
за 20 хвилин
. Визначити енергію активації.
Рішення:
Для реакції першого порядку використовують рівняння:
 (7) (7)
де х
- ступінь перетворення;
τ - час;
k
- константа швидкості реакції
 1/хв. 1/хв.
 1/хв. 1/хв.
Енергію активації знаходимо з рівняння Ареніуса:
 (8) (8)
де R
- універсальна газова постійна (8,31) 

Відповідь:
Енергія активації дорівнює 34,6 кдж/ моль
Дослідження активності радіоактивного препарату показало, що за 10 днів активність його зменшилася на 8,5%. Визначити константу швидкості реакції і час, протягом якого він розкладеться на 75%., якщо реакція розкладання має перший порядок.
Рішення:
Припускаючи, що розкладання йде по мономолекулярному закону
 дня
-1 дня
-1
Час, протягом якого препарат розкладеться на 75%, визначаємо з рівняння константи швидкості реакції, у якому С
х
=75
 дня дня
Відповідь:
Константа швидкості реакції дорівнює3,7∙ 104
година
-1
; 75% препарату розкладеться протягом 259 днів.
В скільки разів збільшиться швидкість розчинення заліза в соляній кислоті при підвищенні температури з 25 до 350
С, якщо температурний коефіцієнт швидкості розчинення  дорівнює 2,8. дорівнює 2,8.
Рішення:
 (9) (9)
 рази рази
На підставі експериментальних даних побудувати кінетичні криві, розрахувати енергію активації і підібрати рівняння для топохімічної реакції, що характеризує кінетику перетворення, використовуючи моделі рівнянь, запропоновані Гістлінгом.
хімічна адсорбція кінетика реакція
Таблиця 1.
Експериментальні дані
| Час, τ
мін. |
Ступінь перетворення, частки одиниці, Т=3000
С
|
Ступінь перетворення, частки одиниці, Т=3500
С
|
| 0 |
0 |
0 |
| 1 |
0,215 |
0, 196 |
| 2 |
0,489 |
0,461 |
| 3 |
0,672 |
0,705 |
| 4 |
0,85 |
0,949 |
| 5 |
0,946 |
0,985 |
| 6 |
0,97 |
0,992 |
| 7 |
0,983 |
0,996 |
| 8 |
0,991 |
0,998 |
| 9 |
0,992 |
0,999 |
| 10 |
0,995 |
1 |
Для рішення задачі скористаємося рівняннями Гінстлінга, що характеризують кінетику перетворень у сумішах твердих речовин і які дозволяють одержувати результати, у достатній мірі наближені до реальних. Ці рівняння виведені для наступних спрощених умов:
1) анізотропія компонентів реакційної суміші не впливає на кінетику процесу;
2) зерна реагентів практично рівновеликі, а форма їх близька до правильної (кульової або кубічної);
3) швидкість процесу не лімітується теплообміном між реагуючими речовинами і навколишнім середовищем і не залежить від швидкості плавлення або кристалізації;
4) масопередача здійснюється в результаті руху часток лише одного компонента (унаслідок великого розходження в рухливості часток реагентів);
5) шар твердого продукту реакції відділений від реагуючого компонента різкою границею;
6) процес квазістаціонарний, саморегулюючий - швидкість усіх його стадій залежить від швидкості самої повільної з них.
Рівняння різні для кінетичної області (тобто в умовах, коли лімітуючою стадією процесу є власне хімічна реакція), для області сублімації (випару), дифузійної і проміжної областей.
Механізм 1 застосуємо, якщо в міру плину реакції зменшується обсяг зерен, а концентрація реагентів на поверхні контакту залишається постійною:
Інтегральна форма рівняння має вигляд:
 (10) (10)
де ά
- ступінь перетворення;
к'
- константа швидкості реакції;
τ
- час.
Механізм 2 застосуємо, коли взаємодія в порошкоподібній суміші яка проходить в кінетичній області, супроводжується не тільки зменшенням поверхні контакту, але і зміною концентрації одного з реагентів і має перший порядок
 (11) (11)
Механізм 3 застосуємо, якщо процес лімітується сублімацією або випаром, тобто протікає в дифузійній області:
 (12) (12)
Механізм 4 застосуємо, коли один з реагентів дифундує через шар твердого продукту реакції:
 (13) (13)
Рішення:
За даними таблиці 1 будуємо кінетичні криві для заданих температур 300 і 3500
С
відповідно (мал.1).
На підставі графічних залежностей ступеня перетворення вихідної речовини від часу τ
(мал.1) визначаємо швидкість процесу:
 (14) (14)
де W
- відносна швидкість реакції, 1/сек.
При температурі 3000
С
:

При температурі 3500
С
:


Рис.1. Графічна залежність  від часу за механізмом 1 від часу за механізмом 1
Для визначення енергії активації будуємо графічну залежність ln Wвід 1/Т
(рис.2).
Т
, 0
С
Т
, К
1/T
300 573 1,7∙10-3
350 623 1,6∙10-3
ln W
300
= ln
0,16 = - 1,83ln W
350
= ln
0,25 = - 1,38

Рис.2. Графічна залежність  від часу за механізмом 1 при температурі 3000
С від часу за механізмом 1 при температурі 3000
С
 (15) (15)

Для визначення механізму реакції будуємо графічні залежності по кожному з рівнянь (101-104) у координатах  від часу τ
. від часу τ
.
Розрахункові значення по механізму 1 представлені в таблиці 2.
Таблиця 2.
Розрахункові значення 
| Час, τ хв
. |
Ступінь перетворення, частки одиниці, Т=3000
С
|

Т
=3000
С
|
Ступінь перетворення, частки одиниці, Т=3500
С
|

Т
=3500
С
|
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0,215 |
0,070 |
0, 196 |
0,070 |
| 2 |
0,489 |
0,186 |
0,461 |
0,186 |
| 3 |
0,672 |
0,334 |
0,705 |
0,334 |
| 4 |
0,850 |
0,629 |
0,949 |
0,629 |
| 5 |
0,946 |
0,753 |
0,985 |
0,753 |
| 6 |
0,970 |
0,800 |
0,992 |
0,800 |
| 7 |
0,983 |
0,841 |
0,996 |
0,841 |
| 8 |
0,991 |
0,874 |
0,998 |
0,874 |
| 9 |
0,992 |
0,900 |
0,999 |
0,900 |
| 10 |
0,995 |
1 |
1 |
1 |

Рис.3. Графічна залежність  від часу за механізмом 1 від часу за механізмом 1

Рис.4. Графічна залежність  від часу за механізмом 1 від часу за механізмом 1
Розрахункові значення по механізму 2 представлені в таблиці 3.
Таблиця 3.
Розрахункові значення 
| Час, τ хв
. |
Ступінь перетворення, частки одиниці, Т=3000
С
|

Т
=3000
С
|
Ступінь перетворення, частки одиниці, Т=3500
С
|

Т
=3500
С
|
| 0 |
0 |
1 |
0 |
1 |
| 1 |
0,215 |
1,175 |
0, 196 |
1,156 |
| 2 |
0,489 |
1,564 |
0,461 |
1,509 |
| 3 |
0,672 |
2,102 |
0,705 |
2,256 |
| 4 |
0,850 |
3,542 |
0,949 |
7,271 |
| 5 |
0,946 |
6,999 |
0,985 |
16,441 |
| 6 |
0,970 |
10,357 |
0,992 |
25,000 |
| 7 |
0,983 |
15,125 |
0,996 |
39,685 |
| 8 |
0,991 |
23,112 |
0,998 |
62,996 |
| 9 |
0,992 |
25 |
0,999 |
100 |
| 10 |
0,995 |
34, 199 |
1 |

Рис.5. Графічна залежність  від часу за механізмом 2 від часу за механізмом 2

Рис.6. Графічна залежність  від часу за механізмом 2 від часу за механізмом 2
Розрахункові значення по механізму 3 представлені в таблиці 4.
Таблиця 4.
Розрахункові значення 
| Час, τ хв
. |
Ступінь перетворення, частки одиниці, Т=3000
С
|

Т
=3000
С
|
Ступінь перетворення, частки одиниці, Т
=3500
С
|

Т
=3500
С
|
| 0 |
0 |
0 |
0 |
| 1 |
0,215 |
0,149 |
0, 196 |
0 |
| 2 |
0,489 |
0,360 |
0,461 |
0,135 |
| 3 |
0,672 |
0,524 |
0,705 |
0,337 |
| 4 |
0,850 |
0,717 |
0,949 |
0,556 |
| 5 |
0,946 |
0,857 |
0,985 |
0,862 |
| 6 |
0,970 |
0,903 |
0,992 |
0,939 |
| 7 |
0,983 |
0,933 |
0,996 |
0,960 |
| 8 |
0,991 |
0,956 |
0,998 |
0,974 |
| 9 |
0,992 |
0,960 |
0,999 |
0,984 |
| 10 |
0,995 |
0,970 |
1 |
0,990 |

Рис.7. Графічна залежність  від часу за механізмом 3 від часу за механізмом 3

Рис.8. Графічна залежність  від часу за механізмом 3 від часу за механізмом 3
Розрахункові значення по механізму 4 представлені в таблиці 5.
Таблиця 5. Розрахункові значення 
| ас, τ хв
. |
Ступінь перетворення, частки одиниці, Т=3000
С
|

Т
=3000
С
|
Ступінь перетворення, частки одиниці, Т=3500
С
|

Т
=3500
С
|
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0,215 |
0,005 |
0, 196 |
0,004 |
| 2 |
0,489 |
0,034 |
0,461 |
0,030 |
| 3 |
0,672 |
0,076 |
0,705 |
0,086 |
| 4 |
0,850 |
0,151 |
0,949 |
0,229 |
| 5 |
0,946 |
0,226 |
0,985 |
0,282 |
| 6 |
0,970 |
0,256 |
0,992 |
0,298 |
| 7 |
0,983 |
0,278 |
0,996 |
0,310 |
| 8 |
0,991 |
0,296 |
0,998 |
0,318 |
| 9 |
0,992 |
0,298 |
0,999 |
0,324 |
| 10 |
0,995 |
1 |

Рис.9. Графічна залежність  від часу за механізмом 4 від часу за механізмом 4

Рис.10. Графічна залежність  від часу за механізмом 4 від часу за механізмом 4
З аналізу графічних залежностей ступеня перетворення речовини в залежності від часу τ
(рис.10), можна зробити висновок, що для даного процесу рівняння швидкості має вигляд:
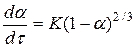 (16) (16)
а залежність між ступенем перетворення (у частках одиниці) вихідної речовини в продукт і часом τ
визначається вираженням (10)
Даний механізм застосовується для процесів які проходять у кінетичній області, якщо протягом реакції змінюється (зменшується) лише поверхня реагуючих зерен, а концентрації взаємодіючих речовин на поверхні їхнього контакту залишаються постійними (наприклад, у випадку газифікації твердого компонента). Це підтверджується і чисельним значенням енергії активації Е
а
= 37,4 кдж/моль
, що вказує на перебіг процесу в області близької до кінетичної.
1. Панченков Г.М., Лебедев В.П. Химическая кинетика и катализ: Учеб. пособие для вузов. Изд.3-е перераб. и дополн. - М.: Химия, 1985. - 592 с.
2. Боре П. Кинетика гетерогенных процессов/ Пер. с француз. - М.: Мир. 1976. - 390 с.
3. Еремин Е.Н. Основы химической кинетики. - М.: Высш. шк., 1976. - 375 с.
4. Позин М.Е., Зинюк Р.Ю. Физико-химическое основы неорганической технологии: Учеб. пособие для вузов. - Л.: Химия. 1985. - 384 с.
5. Царева З.М., Орлова Е.И. Теоретические основы химической технологии. - К.: Вища шк., 1986. - 271 с.
6. Зайцев О.С. Общая химия. Состояние веществ и химические реакции. - М.: Химия. 1990. - 352 с.
|