| ТЕЗ ЕСЕПТЕУ ӘДІСТЕРІ.
Өзектілігі:
тез есептеу әдістерін үйрене отырып , болашақта математикалық білімді жетілдіре отырып, адамның ойлау қабілетін дамыту.
Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамда сапалы және терең білімнің іскерліктің болуын қамтиды. Жастардың белсенді шығармашылық пен жұмыс істеуін және кеңінен ойлауға қабілетті болуын талап етеді. Әрбір адам өз бойындағы туғаннан пайда болған интуициясын әрі қарай дамытуға, табиғи қасиеттерін , математикалық білім деңгейін тереңдету үшін өз бетінше білім алуға қадам басып ұмтылу керек. Менің мақсатым тез есептеу әдістеріне шолу жасай отырып математикалық білімімді арттыру.
Соңғы кезде мектептерде микрокалькуляторлар қолданыла бастады, бірақ олар есептеудің қажеттілігін алып тастай алмайды. Себебі есептеу адамның логикалық ойлауын дамытады, математикаға қызушылығын арттырады.
Осытез есептеу есептеу әдістеріне бірнеше мысал келтірейік.
№1
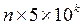 түріндегі көбейтуді ( түріндегі көбейтуді ( - кез келген бүтін сан) ауызша есептеуге мысал келтірейік. Мысалы, 246 - кез келген бүтін сан) ауызша есептеуге мысал келтірейік. Мысалы, 246 5, ол үшін бірінші көбейгішті 2-ге бөліп, екіншісін 2- ге көбейтейік, сонда: 5, ол үшін бірінші көбейгішті 2-ге бөліп, екіншісін 2- ге көбейтейік, сонда:
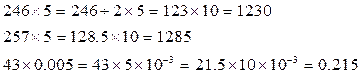
№2
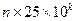 түріндегі көбейтуді ( түріндегі көбейтуді (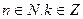 ) орындау. Ол үшін бірінші көбейткішті 100- ге көбейтіп, нәтижесін 4-ке бөлеміз. ) орындау. Ол үшін бірінші көбейткішті 100- ге көбейтіп, нәтижесін 4-ке бөлеміз.
Мысалы:
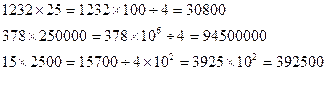
№3
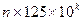 түріндегі көбейтуді ( түріндегі көбейтуді (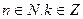 ) орындау. Ол үшін бірінші көбейгішті 1000-ға көбейтіп, нәтижесін 8- ге бөлсе болғаны. ) орындау. Ол үшін бірінші көбейгішті 1000-ға көбейтіп, нәтижесін 8- ге бөлсе болғаны.
Мысалы:
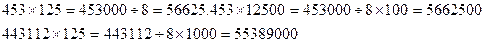
№4
Берілген санды  ; ;  ; ; 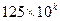 ( (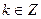 ) түріндегі санға бөлу. Сәйкесінше, бөлінгішті 2-ге, 4-ке, 8 –ге көбейтіп, нәтижесін 10-ға, 100-ге 1000-ға бөлеміз, мысалы: ) түріндегі санға бөлу. Сәйкесінше, бөлінгішті 2-ге, 4-ке, 8 –ге көбейтіп, нәтижесін 10-ға, 100-ге 1000-ға бөлеміз, мысалы:
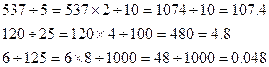
Санды 25- ке бөлудің орнына 100-ге бөлу оңай, ал жүздің ішінде 25 4 рет бар демек, ол 100-ден 4- есе аз, сондықтан нәтижесін 4-ке көбейту керек.:

№5
25- пен аяқталатын сандарды квадрат дәрежеге шығару. Санның квадраттап, оған осы жүздіктің жартысын қосып, қосындыны 10-ға көбейтіп, көбейтіндінің соңына 625-ті тіркеп жазса болғаны, мысалы 325-тің квадратын есептейік:

№6
Екі орынды санды 11-ге көбейту. Ол үшін санның ондығы мен бірлігін қосып, осы қосындыны берілген санның цифрларының арасына жазамыз:
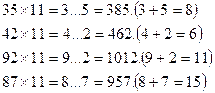
№7
Оңдық цифрлары бірдей, бірліктерінің қосындысы 10-ға тең болатын үш орынды екі санды көбейту тәсілдері. Мысалы:
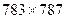 көбейту үшін : көбейту үшін :  , , 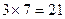 , нәтиже 616221 болады. , нәтиже 616221 болады.
Бұл мынандай түрлендіруге негізделеді:
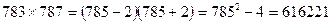
№8
10,11,12,13,14 сандардың өзіндік ерекшліктері.
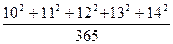 мына есепті ауызша шығару керек. Есеп шыңмен де оңай емес. Есепті шығару үшін сандардың қасиеттерін асқан шеберлікпен пайдаланып, 10,11,12,13,14 сандарының қызығарлықтай ерекшеліктерін көрсете білді. мына есепті ауызша шығару керек. Есеп шыңмен де оңай емес. Есепті шығару үшін сандардың қасиеттерін асқан шеберлікпен пайдаланып, 10,11,12,13,14 сандарының қызығарлықтай ерекшеліктерін көрсете білді.  яғни топтап алдық. Сонда теңдіктің екі жағында да 365-ке тең болды. Яғни яғни топтап алдық. Сонда теңдіктің екі жағында да 365-ке тең болды. Яғни 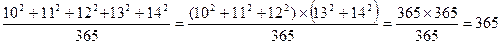 есеп шықты. есеп шықты.
№9 Түбір табуда тез есептеу әдісі . Куб түбір табу.
Куб түбірін тапқанда шығатын санның бірінші цифрын таьу үшін: айтылған санның соңғы 3 цифрын алып тастаймыз да, қалған сан кестеде қандай сандардың кубтарының арасында тұрғанын қараймыз.Осылардың кішісі сол бірінші санды береді. Мысалы, 389017 санынан куб түбір табу керек болсын. Бұл санның соңғы цифры 7, демек , 10-7=3 , бұл іздейтін санның соңғы цифры. Берілген санның соңғы үш цифрын алып тастап, 389 санын аламыз, бұл 7 мен 8-дің кубтарының арасында тұр, мұның кішісі 7. Ендеше, іздеген санымыздың бірінші цифры 7 болды. Сондықтан: 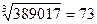 . .
Сондай- ақ бесінші дәрежелі түбір табу. Мысалы 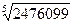 түбірін табу керек. Іздейтін санның соңғы цифры 9. Соңғы 5 цифрын алып тастасақ, 24 шығады, бұл 1 мен 2-нің 5- дәрежелерінің арасында, демек, бірінші цифр 1 болады. Сондықтан түбірін табу керек. Іздейтін санның соңғы цифры 9. Соңғы 5 цифрын алып тастасақ, 24 шығады, бұл 1 мен 2-нің 5- дәрежелерінің арасында, демек, бірінші цифр 1 болады. Сондықтан 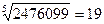
Жетінші дәрежелі түбір табуны қарастырайын. 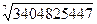 түбірін табу керек. Мұның соңғы цифры 7, 10-7=3 – ізделетін санның соңғы цифры. Түбірдің бірінші цифрын табайық: берілген санның соңғы 7 цифрын алып тастасақ, 340 қалды. Бұл дәреже кестесінде 2 мен 3-тің арасында тұр. Ьұлардың кішісі 2 ендеше түбірден шығатын санның бірінші цифры 2. Сондықтан түбірін табу керек. Мұның соңғы цифры 7, 10-7=3 – ізделетін санның соңғы цифры. Түбірдің бірінші цифрын табайық: берілген санның соңғы 7 цифрын алып тастасақ, 340 қалды. Бұл дәреже кестесінде 2 мен 3-тің арасында тұр. Ьұлардың кішісі 2 ендеше түбірден шығатын санның бірінші цифры 2. Сондықтан 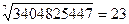 дәлелденді. дәлелденді.
Сан жағынан ұзақ цифрлардан да түбір табуға болады. Сондықтан да тоғызыншы дәрежелі түбір табуды қарастырамын. Мысалы үшін  түбірін табайық. Ізделетін соңғы сан цифры 3. Сонынан 9 цифр алып тастағанда 46411 саны қалды, бұл 9- дәрежелі сандар кестесінде 3 пен 4-тің арасында жатыр. Ендеше түбірін табайық. Ізделетін соңғы сан цифры 3. Сонынан 9 цифр алып тастағанда 46411 саны қалды, бұл 9- дәрежелі сандар кестесінде 3 пен 4-тің арасында жатыр. Ендеше 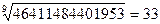 -ке тең болып шықты. -ке тең болып шықты.
№10
11-ге бөлінгіштік белгісі.
Берілген сан 11-ге бөліну үшін ол санның жұп орындағы цифрларының қосындысы мен тақ орындағы цифрларының қосындысының айырмасы не нөл немесе 11-ге бөлінетін сан болуы керек.
Мысалы үшін 92637294 санын 11- ге бөлінгіштік белгісін дәлелдейік.
92637294 санын тез есептеу әдісін қолданайық. Ол үшін бірінші
2+1+2+4=9
9+6+7+9=31
31-9=22
22 11=2 11=2
Яғни бұл сан 11-ге қалдықсыз бөлінетінің дәлелдедім.
№11
13-ке бөлінгіштік белгісі.
Берілген санды солдан оңға қарай сызықшамен үш орынды сандарға бөлеміз. Бірінші, үшінші, бесінші орындағы бөліктердің қосындысын тауып, сол қосындылардың айырмасы 13- ке бөлінсе, онда берілген сан 13-ке бөлінеді.
Мысалы, 91182091 санын тексерейік: 911/820/91, бұдан 911+91=1002 , 1002-820=182 , 182 13-ке бөлінеді, ендеше 91182091 саны да 13-ке бөлінеді.
№12
101- ге бөлінгіштік белгісі
Егер берілген санның, оңнан солға қарай есептегенде, екі- екіден бөлінген цифрларының тақ орындағыларының қосындысы мен жұп орындағыларының қосындысы бірінен бірін азайтқанда айырма не
-ге , не 101- ге тең болса, онда бұл сан 101- ге бөлінеді.
Мысаы 2’, 68’. 45’. 63’, 83 санында 83+45+2=130,63+68=130, 130-130=0 , демек, 268456383 саны 101-ге бөлінеді.
№13.
999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінгіштік белгілері.
Берілген сан 999-ға, 333-ке, 111-ге 37-ге, 27-ге бөлінуі үшін оңнан солға қарай үш- үштен санағанда алғашқы үш бөліктің қосындысы, одан кейінгі үш юөліктің қосындысына тең болса және олар 999,333,111,37, 27-ге бөлінетін болса, ол осы сандарға бөлінеді.
Мысалы 776223-ті тексеріп көрейік: 223+776=999; 999=3 = 9 = 9 111= 111=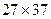 демек, берілген сан 999-ға да, 333-ке де, 11-ге де, 27-ге де бөлінеді. демек, берілген сан 999-ға да, 333-ке де, 11-ге де, 27-ге де бөлінеді.
№14
1001 санын үш орынды кез-келген санға көбейтсек, сол үш орынды санды екі рет қайталап жазғандығыдай нәтиже береді.
Мысалы:
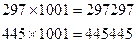
Бұл қарапайым былай есептеледі.
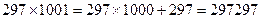
№14
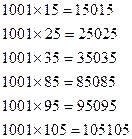 
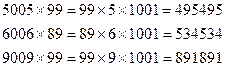
№15
10101 санын екі орынды кез- келген санға көбейтсек, сол екі орынды санды үш рет қайталап жазғандағы нәтижені береді.

№16
1- ден 10-ға дейінгі кез- келген санды 9-ға көбейтіп, шыққан нәтижені 12345679 санына көбейтсек, нәтижесінде алғашқы алынған бір орынды санның 9 рет қайталанып жазылғанын көреміз.
Мысалы, 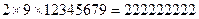
 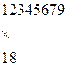
 98765432 98765432
 + 12345679 + 12345679
222222222
№ 17
Екі орынды 5 пен аяқталатын сандардың екінші дәрежесін есептеу үшін 25- ті соңына жазып, ондықты өзінен кейінгі санға көбейтіп шыққан нәтижені жазамыз.
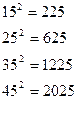 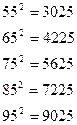
Қорытынды
Қазіргі ғылым мен техникада, күнделікті ісімізге компьютерді, калькуляторды пайдаланып жүрген кезде осы тез есептеу әдістерін қолдану қажеті бар ма деген заңды сұрақ тууы да мүмкін.
Дегенмен де жұмысты жеңілдетуді мақсат етіп, ойлау қабілетімізге тежеу қойып отырғанымызды ойладық па ?
Тез есептеулер әдісі адамның қоғам өміріндегі мәні орасан зор.Санай білмей, сандарды қосуды, азайтуды, көбейтуді, бөлуді дұрыс орындай білмей тұрып, сондай- ақ сандардың қасиеттерін және де тез есептеу әдістерін пайдалана алмайтын адамның ақыл- ойы мен адам қоғамының дамуы мүмкін деп ойлауға болмайды. Егер қолыңызда есептеуіш техника, кесте болмай қалса осындай есептеу тәсілдері сізге көмекке келетіні сөзсіз. Сондықтан да бүгінгі осы жобамда келтірген тез есептеу әдістері адам өміріне қажетті және маңызды деп санаймын.
Пайдаланылған әдебиеттер.
1. К.Ш.Шаяхметова «Математикалық мозаика»
2. «Математика для школьников» научно- практический журнал №2 2008 жылы.
3. «Математика Қазақстан мектебінде» №1 2009 жылы
4. «Математика» республикалық ғылыми әдістемелік журнал.
5. Бабинская И. Л.И. «Математикалық олимпиада есептері »
6. Цыпкин П.А,. «Орта оқу мекемелеріне арналған математикалық анықтама »
|