| 
|
|
| 1.5
|
0.97
|
0.03
|
| 1.4
|
1.3
|
0.95
|
0.05
|
| 1.2
|
1.2
|
0.96
|
0.04
|
| 1.1
|
1
|
0.93
|
0.07
|
| 1.1
|
0.98
|
0.92
|
0.08
|
| 1
|
0.95
|
0.91
|
0.09
|
| 1.1
|
0.93
|
0.9
|
0.1
|
| 1
|
0.9
|
0.9
|
0.11
|
| 1
|
0.93
|
0.89
|
0.11
|
| 1.1
|
0.9
|
0.88
|
0.12
|
| 1
|
0.9
|
0.87
|
0.13
|
| 1.1
|
0.88
|
0.86
|
0.14
|
| 1
|
0.9
|
0.85
|
0.15
|
| 1.1
|
0.88
|
0.84
|
0.16
|
| 1.1
|
0.88
|
0.83
|
0.17
|
| 1.1
|
0.88
|
0.83
|
0.17
|
| 1.1
|
0.9
|
0.82
|
0.18
|
| 1.1
|
0.85
|
0.81
|
0.19
|
| 1.1
|
0.85
|
0.8
|
0.2
|
| 1.1
|
0.85
|
0.8
|
0.2
|
| 1.1
|
0.88
|
0.78
|
0.22
|
| 1.1
|
0.85
|
0.78
|
0.23
|
| 1.2
|
0.88
|
0.77
|
0.23
|
| 1.2
|
0.9
|
0.76
|
0.24
|
| 1.3
|
0.95
|
0.75
|
0.25
|
| 1.4
|
1.05
|
0.74
|
0.26
|
| 1.6
|
1.17
|
0.73
|
0.27
|
| 1.8
|
1.3
|
0.71
|
0.29
|
| 2.2
|
1.55
|
0.7
|
0.3
|
|

|
 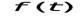 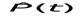 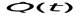
Вариант 21
Задача 1
На испытании находится 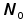 =4000 образцов неремонтируемой аппаратуры. Число отказов =4000 образцов неремонтируемой аппаратуры. Число отказов 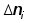 фиксировалось через интервал фиксировалось через интервал 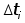
| 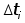 , ч , ч
|
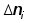
|
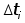 , ч , ч
|
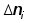
|
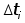 , ч , ч
|
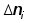
|
| 0..100
|
71
|
1000..1100
|
36
|
2000..2100
|
33
|
| 100..200
|
61
|
1100..1200
|
35
|
2100..2200
|
34
|
| 200..300
|
53
|
1200..1300
|
35
|
2200..2300
|
33
|
| 300..400
|
46
|
1300..1400
|
34
|
2300..2400
|
34
|
| 400..500
|
41
|
1400..1500
|
35
|
2400..2500
|
35
|
| 500..600
|
38
|
1500..1600
|
34
|
2500..2600
|
37
|
| 600..700
|
37
|
1600..1700
|
34
|
2600..2700
|
41
|
| 700..800
|
37
|
1700..1800
|
34
|
2700..2800
|
46
|
| 800..900
|
36
|
1800..1900
|
35
|
2800..2900
|
51
|
| 900..1000
|
35
|
1900..2000
|
33
|
2900..3000
|
61
|
Требуется вычислить значения и построить графики статистических оценок интенсивности отказов 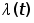 , частоты отказов , частоты отказов 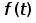 , вероятности безотказной работы P(t) и вероятности отказов Q(t). , вероятности безотказной работы P(t) и вероятности отказов Q(t).
Расчетные формулы

Где 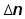 - число отказов в интервале - число отказов в интервале  , ,
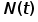 - число объектов , работоспособных к началу интервала - число объектов , работоспособных к началу интервала  . .
 , ,
Где 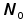 - число объектов, работоспособных в начальный момент времени. - число объектов, работоспособных в начальный момент времени.

Где n - число объектов, отказавших к концу заданного интервала времени за наработку
N - число объектов, работоспособных к началу заданного промежутка времени.

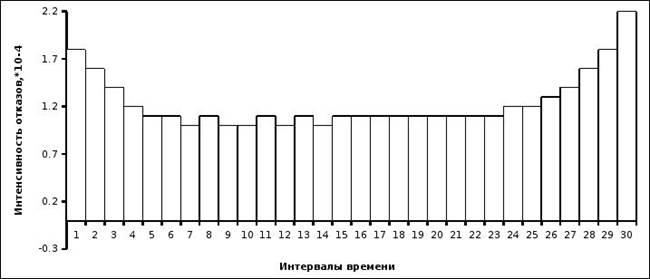
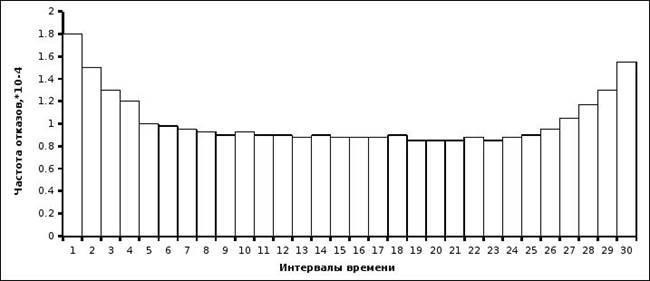
Полученные результаты :
| 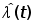
|
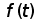
|

|
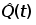
|
| 1
|
1.8
|
1.8
|
0.9823
|
0.0177
|
| 2
|
1.6
|
1.5
|
0.967
|
0.033
|
| 3
|
1.4
|
1.3
|
0.9538
|
0.0462
|
| 4
|
1.2
|
1.1
|
0.9623
|
0.0377
|
| 5
|
1.1
|
1
|
0.932
|
0.068
|
| 6
|
1
|
0.95
|
0.9225
|
0.0775
|
| 7
|
1
|
0.93
|
0.9133
|
0.0867
|
| 8
|
1
|
0.93
|
0.904
|
0.096
|
| 9
|
1
|
0.9
|
0.895
|
0.105
|
| 10
|
0.99
|
0.88
|
0.8863
|
0.1137
|
| 11
|
1
|
0.9
|
0.8773
|
0.1227
|
| 12
|
1
|
0.88
|
0.8685
|
0.1315
|
| 13
|
1
|
0.88
|
0.8598
|
0.1402
|
| 14
|
1
|
0.85
|
0.8513
|
0.1487
|
| 15
|
1
|
0.88
|
0.8425
|
0.1575
|
| 16
|
1
|
0.85
|
0.834
|
0.166
|
| 17
|
1
|
0.85
|
0.8255
|
0.1745
|
| 18
|
1
|
0.85
|
0.817
|
0.183
|
| 19
|
1.1
|
0.88
|
0.8083
|
0.1917
|
| 20
|
1
|
0.83
|
0.8
|
0.2
|
| 21
|
1
|
0.83
|
0.8
|
0.2
|
| 22
|
1.1
|
0.85
|
0.7833
|
0.2167
|
| 23
|
1.1
|
0.83
|
0.775
|
0.225
|
| 24
|
1.1
|
0.85
|
0.7665
|
0.2335
|
| 25
|
1.2
|
0.88
|
0.7573
|
0.2427
|
| 26
|
1.2
|
0.93
|
0.7485
|
0.2515
|
| 27
|
1.4
|
1.02
|
0.7383
|
0.2617
|
| 28
|
1.6
|
1.15
|
0.7268
|
0.2732
|
| 29
|
1.8
|
1.27
|
0.714
|
0.286
|
| 30
|
2.2
|
1.52
|
0.6988
|
0.3012
|
Графики функций приведены ниже.



Задача 2: Для условия задачи 1 вычислить значения средней наработки до отказа в предположении, что :
а) На испытании находились только те образцы, которые отказали.
б) На испытании находилось 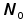 =4000 образцов. =4000 образцов.
Закон распределения наработки до отказа принять показательный.
А) 
где n - число отказавших объектов.
Б)  , ,
Где No - число испытуемых объектов,
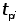 - наработка до отказа i-го объекта. - наработка до отказа i-го объекта.
А) 
Б) 
Задача 3: Используя функцию надежности, полученную в результате рачета в задаче 1, оценить, какова вероятность того, что РТУ, работавшие безотказно в интервале (0,200ч), не откажет в течении следующего интервала (200,400).

Где  - вероятность безотказной работы в течении наработки от - вероятность безотказной работы в течении наработки от 

Задача 4: По результатам эксплуатации 30 комплектов радиоприемных устройств получены данные об отказах, приведенные в таблице.
| 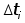 , ч , ч
|
0..100
|
100..200
|
200..300
|
300..400
|
400..500
|
| 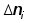
|
30
|
33
|
28
|
26
|
27
|
| 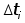 , ч , ч
|
500..600
|
600..700
|
700..800
|
800..900
|
900..1000
|
| 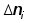
|
28
|
26
|
26
|
28
|
27
|
Требуется :
1 Вычислить значения и построить график статистических оценок параметра потока отказов 
2 Определить вероятность безотказной работы аппаратуры для интервала времени 0.5ч, 2ч, 8ч, 24ч, если наработка аппаратуры с начала эксплуатации
 =1000 ч. =1000 ч.

Где 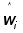 - параметр потока отказов - параметр потока отказов
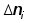 - число отказов N
восстанавливаемых объектов на интервале наработки - число отказов N
восстанавливаемых объектов на интервале наработки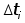
| I
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| w(t) ,
|
0.01
|
0.011
|
0.0093
|
0.0086
|
0.009
|
0.0093
|
0.0086
|
0.0086
|
0.0093
|
0.009
|
Считая поток простейшим приравниваем  . Так как наработка аппаратуры с начала эксплуатации 1000 ч. то в качестве значения . Так как наработка аппаратуры с начала эксплуатации 1000 ч. то в качестве значения 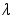 берём численное значение берём численное значение 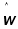 на интервале времени 900-1000 ч. на интервале времени 900-1000 ч.





Задача 5 На основании анализа записей в журнале учета технического состояния и эксплуатации установлено, что за год эксплуатации радиостанции возникло 10 отказов. Время восстановления работоспособности радиостанции после отказа приведено в таблице.
| I
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| t , мин
|
79
|
43
|
33
|
51
|
67
|
39
|
45
|
31
|
46
|
76
|
Требуется определить :
1. Среднее время восстановления ,
2. Интенсивность восстановления 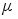 , если время восстановления распределено по показательному закону; , если время восстановления распределено по показательному закону;
3. Вероятность восстановления работоспособности радиостанции за время  ч; ч;  ч; ч;  ч ч

где 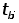 - время восстановления работоспособности после i-го отказа; - время восстановления работоспособности после i-го отказа;
n - количество отказов за рассматриваемый срок эксплуатации








Задача 6 : Используя результаты расчетов, полученные в задаче 5 определить, какое время необходимо оператору для устранения неисправности, чтобы вероятность восстановления за заданное время была не менее а) 0.95 б)0.9.




а) 
б) 
Задача 7 : Радиопередающее устройство состоит из пяти блоков, отказ любого из которых приводит к отказу радиопередающего устройства. Потоки отказов блоков являются простейшими с параметрами :
w1=0.0021 ч-1 w2=0.0042 ч-1 w3=0.0084 ч-1
w4=0.0126 ч-1 w5=0.0147 ч-1
Определить вероятность того, что за один час работы в радиопередающем устройстве :
А) не появится ни одного отказа;
Б) появится хотя бы один отказ;
В) появится один отказ.
Так как , поток простейший 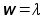 . .
Вероятность безотказной работы






А) 

Б) 
В) 

Задание 8
Рассчитать вероятность безотказной работы в течении наработки  РТУ. РТУ.
Структурная схема расчета надёжности РТУ приведена на рисунке
 ; ;  ; ;  ; ;  ; ; 








|