| Содержание
1. Задача №1……………………………………………………….……………..3
2. Задача №2………………………………………………………………...……6
3. Задача №3………………………………………………………………...……7
4. Задача №4…………………………………………………………………….10
5. Задача №5………………………………………………………………….…14
6. Задача №6…………………………………………………………………….16
7. Задача №7…………………………………………………………………….19
8. Задача №8…………………………………………………………………….21
9. Список литературы……………………………………………….…………23
Задача № 1
Имеются данные о размере активов коммерческих банков и величине балансовой прибыли на 01.10.01:
| № п/п
|
Активы на 01.10.01, млн. руб.
|
Балансовая прибыль, млн. руб.
|
| 1
|
1510
|
28
|
| 2
|
1315
|
3
|
| 3
|
1522
|
17
|
| 4
|
1520
|
8
|
| 5
|
1487
|
17
|
| 6
|
1517
|
9
|
| 7
|
1517
|
18
|
| 8
|
1427
|
3
|
| 9
|
1496
|
43
|
| 10
|
1488
|
3
|
| 11
|
1354
|
0
|
| 12
|
1477
|
3
|
| 13
|
1476
|
4
|
| 14
|
1525
|
40
|
| 15
|
1468
|
15
|
| 16
|
1442
|
10
|
| 17
|
1345
|
1
|
| 18
|
1426
|
29
|
| 19
|
1426
|
3
|
| 20
|
1414
|
33
|
| 21
|
1408
|
1
|
| 22
|
1407
|
42
|
| 23
|
1394
|
6
|
| 24
|
1368
|
7
|
| 25
|
1367
|
47
|
Для изучения зависимости между размером активов коммерческих банков и величиной балансовой прибыли произведите группировку банков по размеру активов, выделив пять групп с равными интервалами. По каждой группе и в целом по совокупности подсчитайте:
1) число банков;
2) средний размер активов – всего и на один банк;
3) среднюю величину балансовой прибыли – всего и на один банк.
Результаты группировки необходимо представить в аналитической таблице, сделать выводы.
Решение:
Прежде всего определим величину интервала:
i
=  = = 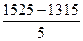 = 42 (млн. руб.) = 42 (млн. руб.)
Производим группировку предприятий по активам с интервалом в 42 млн. руб., для чего строим рабочую таблицу.
Распределение предприятий по активам
| № п/п
|
Группы предприятий по активам, млн. руб.
|
№ предприятия
|
Активы на 01.10.01, млн. руб.
|
Балансовая прибыль, млн. руб.
|
| А
|
1
|
2
|
3
|
|
| |
|
2
|
1315
|
3
|
| I
|
1315-1357
|
17
|
1345
|
1
|
| |
|
11
|
1354
|
0
|
| Итого по группе I
|
|
3
7
|
4014
|
4
|
| |
|
25
|
1367
|
47
|
| II
|
1358-1399
|
24
|
1368
|
7
|
| |
|
23
|
1394
|
6
|
| Итого по группе II
|
|
3
|
4129
|
60
|
| |
|
22
|
1407
|
42
|
| |
|
21
|
1408
|
1
|
| |
|
20
|
1414
|
33
|
| III
|
1400-1441
|
18
|
1426
|
29
|
| |
|
19
|
1426
|
3
|
| |
|
8
|
1427
|
3
|
| Итого по группе III
|
|
6
|
8508
|
111
|
| |
|
16
|
1442
|
10
|
| |
|
15
|
1468
|
15
|
| IV
|
1441-1483
|
13
|
1476
|
4
|
| |
|
12
|
1477
|
3
|
| Итого по группе IV
|
|
4
|
5863
|
32
|
| V
|
|
5
|
1487
|
17
|
| |
10
|
1488
|
3
|
| |
9
|
1496
|
43
|
| 1484-1525
|
1
|
1510
|
28
|
| |
6
|
1517
|
9
|
| |
7
|
1517
|
18
|
| |
4
|
1520
|
8
|
| А
|
|
1
|
2
|
3
|
| |
|
3
|
1522
|
17
|
| |
14
|
1525
|
40
|
| Итого по группе V
|
|
9
|
13582
|
183
|
| ВСЕГО
|
25
|
36096
|
390
|
Для установления наличия и характера связи между суммами активов и балансовой прибылью по данным рабочей таблицы строим итоговую аналитическую таблицу.
Зависимость балансовой прибыли от суммы активов
| № п/п
|
Группы предприятий по сумме активов, млн. руб.
|
Число предприятий
|
Сумма активов, млн. руб.
|
Балансовая прибыль, млн. руб.
|
| всего
|
в среднем на одно предприятие
|
всего
|
в среднем на одно предприятие
|
| А
|
Б
|
1
|
2
|
3
|
4
|
5
|
| 1.
|
1315-1357
|
3
|
4014
|
1338
|
4
|
1,33
|
| 2.
|
1358-1399
|
3
|
4129
|
1376,33
|
60
|
20
|
| 3.
|
1400-1441
|
6
|
8508
|
1418
|
111
|
18,5
|
| 4.
|
1441-1483
|
4
|
5863
|
1465,75
|
32
|
8
|
| 5.
|
1484-1525
|
9
|
13582
|
1509,11
|
183
|
20,33
|
| |
Итого
|
25
|
36096
|
1443,84
|
390
|
15,6
|
Данные таблицы показывают, что между размером активов коммерческих банков и величиной балансовой прибыли нет устойчивой зависимости.
Задача № 2
Имеются следующие данные по озимым зерновым культурам, выращенным на территории РФ всеми видами хозяйств:
| Культура (озимая)
|
1999г.
|
2000г.
|
| Урожайность, ц/га
|
Посевная площадь, тыс. га
|
Урожайность, ц/га
|
Посевная площадь, тыс. га
|
| Пшеница
|
16,1
|
8246
|
21,3
|
7609
|
| Рожь
|
8,6
|
3762
|
14,1
|
3385
|
| Ячмень
|
24,7
|
345
|
34,5
|
419
|
Вычислите среднюю урожайность зерновых культур:
1) за 1999 год;
2) за 2000 год.
Укажите, какой вид средней необходимо применить для вычисления этих показателей.
Решение:
Для решения задачи воспользуемся формулой средней арифметической взвешенной:
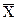 = = 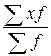
Рассчитаем среднюю урожайность зерновых культур за 1999 год:
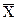 = =  = =  = 14,06 ц/га = 14,06 ц/га
Рассчитаем среднюю урожайность зерновых культур за 2000 год:
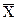 = =  = = 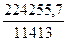 = 19,65 ц/га = 19,65 ц/га
Итак, в 1999 году средняя урожайность зерновых культур составляла 14,06 ц/га, а в 2000 увеличилась и составила 19,65 ц/га.
Задача № 3
Для изучения возрастной проблемы безработицы в одном из поселков городского типа Челябинской области было проведено 5%-ное выборочное обследование 100 безработных, отобранных в случайном порядке, в результате которого получены следующие данные:
| Возраст безработного
|
Всего человек
|
| До 20 лет
|
7
|
| 20-24
|
13
|
| 24-28
|
15
|
| 28-32
|
18
|
| 32-36
|
16
|
| 36-40
|
12
|
| 40-44
|
10
|
| Свыше 44 лет
|
9
|
| Итого
|
100
|
На основе этих данных вычислите:
1. Средний возраст безработных способом моментов.
2. Средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0,997 предельную ошибку выборочной средней и возможные границы среднего возраста безработного в поселке.
5. С вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса количества безработных в возрасте от 24 до 40 лет.
Напишите краткие выводы.
Решение:
Суть способа «моментов» заключается в том, что:
1) из всех вариант вычитается постоянное число «А» (значение серединной варианты или варианты, имеющей наибольшую величину);
2) все варианты делятся на постоянное число, а именно: на величину интервала (i
).
Получаем новую среднюю, которая называется моментом первого порядка (m1
):
m1
= , ,
тогда средняя арифметическая будет равна 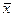 = = 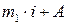
Для расчета среднего квадратического отклонения находим момент второго порядка (m2
):
m2
= 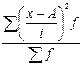 , ,
и среднее квадратическое отклонение будет равно:
σ = i
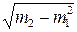
Для расчета среднего возраста безработных и среднего квадратического отклонения строим расчетную таблицу.
Расчет среднего квадратического отклонения
способом «моментов»
| Группы по возрасту
|
Число человек
|
x
|
x-А
|
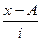
|
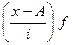
|

|
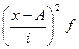
|
| А
|
Б
|
1
|
2
|
3
|
4
|
5
|
6
|
| До 20 лет
|
7
|
18
|
-12
|
-3
|
-21
|
9
|
63
|
| 20-24
|
13
|
22
|
-8
|
-2
|
-26
|
4
|
52
|
| 24-28
|
15
|
26
|
-4
|
-1
|
-15
|
1
|
15
|
| 28-32
|
18
|
30
|
0
|
0
|
0
|
0
|
0
|
| 32-36
|
16
|
34
|
4
|
1
|
16
|
1
|
16
|
| 36-40
|
12
|
38
|
8
|
2
|
24
|
4
|
48
|
| 40-44
|
10
|
42
|
12
|
3
|
30
|
9
|
90
|
| Свыше 44 лет
|
9
|
46
|
16
|
4
|
36
|
16
|
144
|
| Итого:
|
100
|
–
|
–
|
–
|
44
|
–
|
428
|
А
= 30 по наибольшей частоте
i
= 4
m1
= 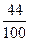 = 0,44; = 0,44;
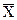 = = 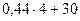 = 31,76 года = 31,76 года
Средний возраст безработных составил 31,76 года
m2
=  = 4,28 = 4,28
σ = 4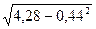 = 4 = 4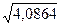 = 8,09 года = 8,09 года
Тогда, средний квадрат отклонений 8,092
=65,45
3. Относительный показатель вариации – коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
V = 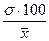 . .
По величине коэффициента вариации можно судить о степени вариации признаков, а, следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу:
V =  = 25,5%. = 25,5%.
Небольшая колеблемость признака, то есть средний возраст безработных 31,76 года, – реальная величина и может представлять данную группу.
4. Ошибка выборочного наблюдения определяется по формуле:
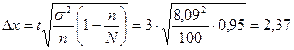 года; года;

С вероятностью 0,997 можно утверждать, что средний возраст безработных находится в пределах от 29,39 до 34,13 года.
1. Определим долю безработных такого возраста в выборочной совокупности:
w = 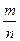 = = 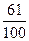 = 0,61 или 61%. = 0,61 или 61%.
Из 100 безработных 61% в возрасте от 24 до 40 лет.
Определим предельную ошибку выборочного наблюдения:
Δw
= t 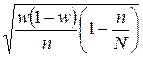
или Δw
= 3 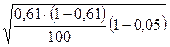 = 0,143 или14,3%. = 0,143 или14,3%.
Доверительные интервалы для доли будут равны:
p = w Δw Δw
p = 61%  14,3%, тогда 61% – 14,3% 14,3%, тогда 61% – 14,3% 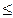 p p 61% + 14,3%. 61% + 14,3%.
Доля безработных в возрасте от 24 до 40 лет будет находиться в пределах от 46,7 до 75,3% при вероятности 0,997.
Выводы: Средний возраст безработных составил 31,76 года. Значение коэффициента вариации свидетельствует об однородности выборочной совокупности, т.е. средняя величина надежная, типичная для данной совокупности. Рассчитанные пределы средней совпадают с данными таблицы. От 46,7 до 75,3% безработных в изучаемой выборочной совокупности имеют возраст от 24 до 40 лет.
Задача № 4
Денежные доходы населения (в деноминированных рублях) в РФ характеризуются следующими данными, млрд. руб.:
| Годы
|
Денежные доходы, млрд. руб.
|
| 1997
|
7,1
|
| 2002
|
364,8
|
| 2003
|
910,7
|
| 2004
|
1350,2
|
| 2005
|
1641,6
|
| 2006
|
1751,4
|
| 2007
|
2748
|
Для анализа динамики денежных доходов населения в Российской Федерации за 2002-2007 гг. вычислите:
1. Абсолютные приросты, темпы роста и темпы прироста (цепные и базисные), абсолютное содержание одного процента прироста.
Полученные показатели представьте в виде таблицы.
2. Среднегодовой доход населения.
3. Среднегодовой темп роста и прироста доходов населения за 1997-2002 гг. и за 2002-2007 гг.
4. Постройте график динамики доходов населения в РФ за 1997-2007 гг.
Напишите краткие выводы.
Решение:
1) Определим абсолютные приросты:
цепные базисные
 yц
= уi
–
yi
-
1 yц
= уi
–
yi
-
1
 yб
= уi
–
yо yб
= уi
–
yо
 y2003
=910,7–364,8=545,9 млрд. руб. y2003
=910,7–364,8=545,9 млрд. руб.  y2003
=910,7–364,8=545,9млрд. руб. y2003
=910,7–364,8=545,9млрд. руб.
 y2004
=1350,2-910,7=439,5 млрд. руб. y2004
=1350,2-910,7=439,5 млрд. руб.  y2004
=1350,2–364,8=985,4млрд.руб. y2004
=1350,2–364,8=985,4млрд.руб.
 y2005
=1641,6-1350,2=291,4млрд. руб. y2005
=1641,6-1350,2=291,4млрд. руб.  y2005
=1641,6–364,8=1276,8млрд.руб. y2005
=1641,6–364,8=1276,8млрд.руб.
 y2006
=1751,4-1641,6=109,8 млрд. руб. y2006
=1751,4-1641,6=109,8 млрд. руб.  y2006
=1751,4–364,8=1386,6 млрд. руб. y2006
=1751,4–364,8=1386,6 млрд. руб.
 y2007
=2748-1751,4=996,6 млрд. руб. y2007
=2748-1751,4=996,6 млрд. руб.  y2007
=2748–364,8=2383,2 млрд. руб. y2007
=2748–364,8=2383,2 млрд. руб.
Определим темпы роста:
цепные базисные
k = 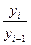 k = k = 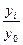
k2003
=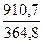 =2,496 k2003
= =2,496 k2003
=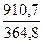 =2,496 =2,496
k2004
=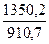 =1,483 k2004
= =1,483 k2004
= =3,701 =3,701
k2005
= =1,216 k2005
= =1,216 k2005
=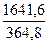 =4,5 =4,5
k2006
=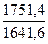 =1,067 k2006
= =1,067 k2006
= =4,801 =4,801
k2007
= =1,569 k2007
= =1,569 k2007
= =7,533 =7,533
Определим темпы прироста:
цепные базисные
Δkц
= kц
% – 100 Δkб
= k % – 100
Δk2003
=249,6–100=149,6 % Δk2003
=249,6–100=149,6 %
Δk2004
=148,3–100=48,3 % Δk2004
=370,1–100=270,1 %
Δk2005
=121,6–100=21,6 % Δk2005
=450–100=350 %
Δk2006
=106,7–100=6,7 % Δk2006
=480,1–100=380,1 %
Δk2007
=156,9–100=56,9 % Δk2007
=753,3–100=653,3 %
Определим абсолютное значение одного процента прироста:
А
%
=  или А
%
= 0,01 у
i
-
1 или А
%
= 0,01 у
i
-
1
А
%
2003
=3,648 млрд. руб.
А
%
2004
=9,107 млрд. руб.
А
%
2005
=13,502 млрд. руб.
А
%
2006
=16,416 млрд. руб.
А
%
2007
=17,514 млрд. руб.
Все перечисленные показатели динамики оформляем в итоговую таблицу.
Показатели динамики денежных доходов населения в Российской Федерации за 2002-2007 гг.
| Год
|
Денежные доходы, млрд. руб.
|
Абсолютные приросты,
млрд. руб
|
Темпы роста, %
|
Темпы прироста, %
|
Абсолют. значение 1% прироста, млрд. руб
|
| цепные (ежегод.)
|
базисные (к 2002г.)
|
цепные (ежегод.)
|
базисные (к 2002г.)
|
цепные (ежегод.)
|
базисные
(к 2002г.)
|
| А
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| 2002
2003
2004
2005
2006
2007
|
364,8
910,7
1350,2
1641,6
1751,4
2748
|
–
545,9
439,5
291,4
109,8
996,6
|
–
545,9
985,4
1276,8
1386,6
2383,2
|
–
249,6
148,3
121,6
106,7
156,9
|
–
249,6
370,1
450,0
480,1
753,3
|
–
149,6
48,3
21,6
6,7
56,9
|
–
149,6
270,1
350,0
380,1
653,3
|
–
3,648
9,107
13,502
16,416
17,514
|
2) Среднегодовой доход населения
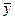 = =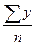 = =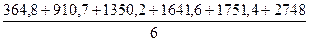 =1461,12 млрд. руб. =1461,12 млрд. руб.
3) Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
= = =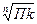 , ,
где n
– число цепных темпов роста;
П
– знак произведения;
=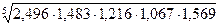 = =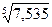 =1,498 или 149,8 %. =1,498 или 149,8 %.
Среднегодовой темп роста за 2002-2007гг. равен 149,8 %.
Среднегодовой темп прироста исчисляется следующим образом:
Δ = % – 100%=149,8–100=49,8%.
Таким образом, доход населения за период 2002-2007гг увеличивался за год в среднем на 49,8%.
За 1997-2002 гг.среднегодовой темп роста равен 270 %
Среднегодовой темп прироста:
Δ = % – 100%=270–100= 170%.
Построим график доходов населения за 1997-2007 гг
 Рис. 1. График доходов населения за 1997-2007гг
Итак, доход населения за период 2002-2007гг увеличивался за год в среднем на 49,8%. По сравнению с 2002 годом это увеличение составило 2383,2 млрд.руб. или на 653,3 %.
Динамика доходов населения за исследуемый период положительная.
Задача № 5
Имеются следующие данные об остатках вкладов населения в банках г.г. Челябинска и Екатеринбурга:
| Город
|
Остаток вклада, млн. руб.
|
| 01.01
|
01.02
|
01.03
|
01.04
|
01.05
|
01.06
|
01.07
|
| Челябинск
|
15
|
16
|
17
|
16,5
|
16,7
|
16
|
17,4
|
| Екатеринбург
|
20
|
21
|
23
|
21,5
|
21,8
|
21,1
|
23,5
|
| Итого
|
35
|
37
|
40
|
38
|
38,5
|
37,1
|
40,9
|
Вычислите среднюю величину остатка вкладов по каждому городу и по двум городам вместе:
а) за каждый квартал;
б) за полугодие.
Решение:
Применяем формулу средней хронологической:

Средняя величина остатка вкладов за первый квартал по банкам Челябинска:

Средняя величина остатка вкладов за первый квартал по банкам Екатеринбурга:
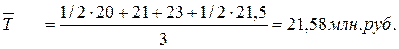
Средняя величина остатка вкладов за первый квартал по банкам двух городов вместе:

Средняя величина остатка вкладов за второй квартал по банкам Челябинска:
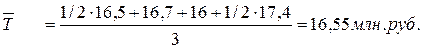
Средняя величина остатка вкладов за второй квартал по банкам Екатеринбурга:
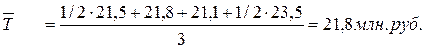
Средняя величина остатка вкладов за второй квартал по банкам двух городов вместе:
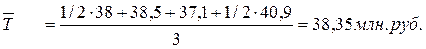
Средняя величина остатка вкладов за полугодие по банкам Челябинска:

Средняя величина остатка вкладов за полугодие по банкам Екатеринбурга:
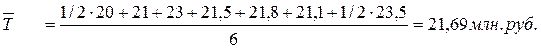
Средняя величина остатка вкладов за полугодие по банкам двух городов вместе:
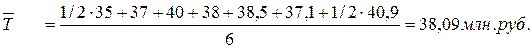
Задача № 6
Динамика средних цен и объема продажи сельхозпродукции фермерскими хозяйствами и сельхозпредприятиями РФ характеризуется следующими данными:
| Наименование продукции
|
Продано товара за период, тыс. т
|
Средняя цена за период, руб. т
|
| базисный
|
отчетный
|
базисный
|
отчетный
|
| Сельхозпредприятия:
Картофель
Мясо
|
800
2000
|
700
1700
|
1225
6296
|
3714
14950
|
| Фермерские хозяйства:
Картофель
|
303
|
316
|
1190
|
3600
|
На основании имеющихся данных вычислите:
1. Для сельхозпредприятий (по всем видам продукции):
а) общий индекс товарооборота;
б) общий индекс цен;
в) общий индекс физического объема товарооборота.
Определите в отчетном периоде прирост товарооборота и разложите его по факторам (за счет изменения цен и объема реализации).
Покажите взаимосвязь между исчисленными индексами.
2. Для сельхозпредприятий и фермерских хозяйств вместе (по картофелю) определить:
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры объема продаж выбранного вида продукции на динамику средней цены.
Напишите краткие выводы.
Решение:
1. Общий индекс товарооборота в фактических ценах:
Ipq
= 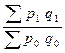 = = 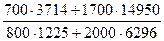 = = 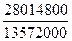 = 2,064 или 206,4%. = 2,064 или 206,4%.
Товарооборот сельхозпредприятий в фактических ценах увеличился в отчетном году по сравнению с базисным на 106,4%.
Формула агрегатного индекса цен будет выглядеть следующим образом:
Ip
= 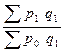 = = 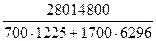 = = 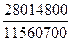 = 2,423 или 242,3%. = 2,423 или 242,3%.
В целом цены на товары в отчетном году по сравнению с базисным по сельхозпредприятиям выросли на 142,3%.
Индекс физического объема товарооборота:
I
q
= 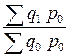 = = 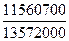 = 0,852 или 85,2%, = 0,852 или 85,2%,
то есть объем продаж сельхозпродукции сельхозпредприятиями в отчетном году по сравнению с базисным уменьшился в целом на 14,8%.
Разность между числителем и знаменателем индекса товарооборота в фактических ценах дает прирост (или снижение) товарооборота в абсолютной сумме:
Δpq
= 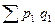 – –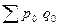 = 28014800-13572000 = 14442800 (тыс. руб.). = 28014800-13572000 = 14442800 (тыс. руб.).
Разность между числителем и знаменателем индекса цен дает прирост (снижение) товарооборота за счет изменения цен:
Δpq(p)
=  – –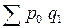 = 28014800-11560700 = 16454100 (тыс. руб.). = 28014800-11560700 = 16454100 (тыс. руб.).
Прирост товарооборота в абсолютной сумме в отчетном году по сельхозпредприятиям составил 16454100 тыс. рублей за счет увеличения цен на 142,3%.
Разность между числителем и знаменателем индекса физического объема товарооборота дает прирост (или снижение) товарооборота в неизменных ценах:
Δpq(q)
= 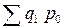 – – = 11560700-13572000 = -2011300 (тыс. руб.). = 11560700-13572000 = -2011300 (тыс. руб.).
Уменьшение товарооборота в абсолютной сумме в отчетном году по сельхозпредприятиям за счет уменьшения количества проданной продукции на 14,8% составило 2011300 тыс. руб.
Связь между изменениями объема товарооборота, количеством продажи товаров и уровнем их цен выражается в системе взаимосвязанных индексов:
 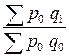 = =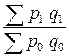
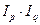 = I
pq
, = I
pq
,
тогда в нашей задаче:
2,423·0,852=2,064
2. Индекс цен переменного состава:
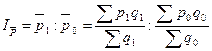 . .
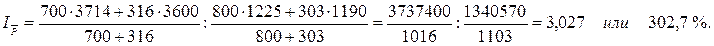
Индекс цен постоянного состава:

Следующий расчет - индекс структурных сдвигов
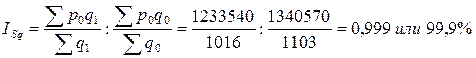
Следовательно, средняя цена на картофель возросла на 202,7 %,
в том числе за счет динамики цен по рынкам - на 303 %,
а структурные изменения в количестве товара по рынкам привели к уменьшению средней цены на 0,1 %.
Задача № 7
Имеются следующие данные по затратам на производство тканей за 1998-1999 гг.:
| Вид ткани
|
Затраты на производство продукции, млн. руб.
|
Изменение количества произведенной продукции, %
|
| 1999г.
|
2000г.
|
| Хлопчатобумажные
|
32400
|
53046
|
+16,9
|
| Шерстяные
|
2358
|
4588,8
|
+21,6
|
| Шелковые
|
9990
|
21312
|
+33,3
|
| Льняные
|
4788
|
10745,7
|
+32,0
|
Вычислите:
1. Общий индекс затрат на производство тканей в фактических ценах.
2. Общий индекс физического объема по производству продукции.
3. Общий индекс себестоимости, используя взаимосвязь исчисленных индексов.
Напишите краткие выводы.
Решение:
Индексная система затрат на производство продукции.
 , ,
где Izq
- индекс общих з
атрат на производство,
z
0
;
z
1
- себестоимость единицы п
родукции в базисном и отчетном периодах;
q0
; q1
- количество продукции в базисном и отчетном периодах;
z
0
q
0
;
z
1
q
1
- затраты на производство продукции в базисном и отчетном периодах;
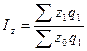 - общий индекс себестоимости; - общий индекс себестоимости;
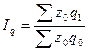 - общий индекс физического объема продукции. - общий индекс физического объема продукции.
Общий индекс затрат на производство тканей в фактических ценах:
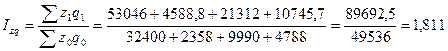
Общий индекс физического объема производства тканей:
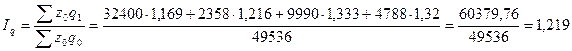
Общий индекс себестоимости производства тканей

Итак, в 2000 году по сравнению с 1999 годом затраты на производство тканей в фактических ценах возросли на 81,1%. При этом себестоимость возросла на 48,6%, а объем производства увеличился на 21,9%.
Задача № 8
Для изучения тесноты связи между балансовой прибылью (результативный признак – У) и его активами (факторный признак – Х) по данным задачи № 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значение.
Решение:
Для расчета межгрупповой дисперсии строим расчетную таблицу.
| Группы предприятий по сумме активов, млн. руб.
|
Число предприятий
|
Балансовая прибыль, млн. руб.на 1 предприятие
|
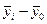
|
(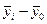 )2 )2
|
( )2
n )2
n
|
| 1315-1357
|
3
|
1,33
|
-14,27
|
203,6329
|
610,8987
|
| 1358-1399
|
3
|
20
|
4,4
|
19,36
|
58,08
|
| 1400-1441
|
6
|
18,5
|
2,9
|
8,41
|
50,46
|
| 1441-1483
|
4
|
8
|
-7,6
|
57,76
|
231,04
|
| 1484-1525
|
9
|
20,33
|
4,73
|
22,3729
|
201,3561
|
| Итого
|
25
|
15,6
|
–
|
–
|
1151,84
|
Рассчитаем межгрупповую дисперсию по формуле
 = =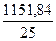 =46,07 =46,07
Для расчета общей дисперсии возведем все значения «у
» в квадрат.
| у
|
у2
|
у
|
у2
|
у
|
у2
|
у
|
у2
|
у
|
у2
|
| 28
|
784
|
9
|
81
|
0
|
0
|
10
|
100
|
1
|
1
|
| 3
|
9
|
18
|
324
|
3
|
9
|
1
|
1
|
42
|
1764
|
| 17
|
289
|
3
|
9
|
4
|
16
|
29
|
841
|
6
|
36
|
| 8
|
64
|
43
|
1849
|
40
|
1600
|
3
|
9
|
7
|
49
|
| 17
|
289
|
3
|
9
|
15
|
225
|
33
|
1089
|
47
|
2209
|
| |
|
|
|
|
|
|
|
|
11656
|
Рассчитаем общую дисперсию по формуле.
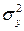 = =  –15,62
= 222,88. –15,62
= 222,88.
Тогда коэффициент детерминации будет:
η2
=  = 0,207 = 0,207
Он означает, что вариация суммы балансовой прибыли на 20,7% объясняется вариацией суммы активов и на79,3% – прочими факторами.
Эмпирическое корреляционное отношение будет равно:
η = 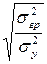 = = 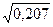 = 0,455 = 0,455
Оно показывает, что связь между балансовой прибылью и суммой активов умеренная.
Литература:
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – М.: Финансы и статистика, 1999.
2. Едонова М.Р., Рябцев В.М. Общая теория статистики. – М.: Юрист, 2001.
3. Практикум по статистике: учебное пособие / под ред. Симчера В.М., М.: Финанстатистинформ, 1999.
4. Батырева Л.В. Общая теория статистики: Учебно-практическое пособие / УрСЭИ АТиСО. – Челябинск, 2003.
|