| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
математический факультет
Кафедра алгебры и геометрии
Курсовая работа
Инвариантные подгруппы бипримарных групп
Исполнитель:
студентка группы H.01.01.01 М-41 Таратын В.В.
Научный руководитель:
доктор физико-математических наук,
профессор кафедры Алгебры и геометрии Монахов В.С.
Гомель 2006
Содержание
Введение
1. Основные обозначения
2. Инвариантные подгруппы бипримарных групп
3. О порядках силовских подгрупп общей линейной группы
Заключение
Список литературы
В настоящей курсовой работе излагается материал на тему: "Инвариантные подгруппы бипримарных групп". Цель этой курсовой работы состоит в том, чтобы исследовать существование примарных нормальных подгрупп в бипримарных группах.
Моя курсовая работа состоит из трех пунктов. В первом пункте изложены основные обозначения, которые используются в данной работе, что значительно упрощает дальнейшую работу и проверку курсовой.
Во втором пункте было рассказано про инвариантные подгруппы бипримарных групп.
В третьем пункте изложен материал о порядках силовских подгрупп общей линейной группы.
Также в этом пункте изучены и доказаны следующие основные теоремы:
Теорема.
Пусть  - конечная разрешимая группа, порядка - конечная разрешимая группа, порядка  , ,  - простое число и - простое число и  не делит не делит  . Если . Если  , то либо , то либо  обладает характеристической обладает характеристической  -подгруппой порядка -подгруппой порядка  , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1)  , ,  и и  делит порядок делит порядок  ; ;
2)  , ,  делит порядок делит порядок  , где , где  - простое число, причем - простое число, причем  , если , если  , и , и  , если , если  ; ;
3)  , ,  1 и 1 и 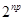 делит порядок делит порядок  . .
Теорема.
Пусть  - группа порядка - группа порядка  , ,  и и  - простые числа. Если - простые числа. Если  , то либо , то либо  обладает характеристической обладает характеристической  -подгруппой порядка -подгруппой порядка  , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1)  , ,  , ,  и и  ; ;
2)  , ,  , ,  , причем , причем  , если , если  , и , и  , если , если  ; ;
3)  , ,  , ,  и и  . .
Теорема.
Группа порядка  , ,  , не имеющая неединичных инвариантных , не имеющая неединичных инвариантных  -подгрупп, существует для каждого из следующих трех случаев: -подгрупп, существует для каждого из следующих трех случаев:
1)  , ,  , ,  и и  ; ;
2)  , ,  , ,  и и  , если , если  , ,  , если , если  ; ;
3)  , ,  , ,  и и  . .
Теорема.
Пусть  и и  - различные простые числа и - различные простые числа и  - порядок силовской - порядок силовской  -подгруппы из группы -подгруппы из группы  . Тогда и только . Тогда и только  , когда выполняется одно из условий: , когда выполняется одно из условий:
1)  , ,  , ,  - любое натуральное число за исключением - любое натуральное число за исключением  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , , 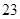 , ,  ; ;
2)  , ,  , ,  - любое натуральное число - любое натуральное число  ; ;
3)  , ,  , ,  - любое натуральное число - любое натуральное число  за исключением за исключением  , где , где  ; ;  , где , где  - любое целое число, удовлетворяющее неравенству - любое целое число, удовлетворяющее неравенству  . Для . Для  дополнительно исключаются числа дополнительно исключаются числа 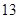 , ,  , , 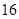 и и  ; для ; для  дополнительно исключаются дополнительно исключаются  и и  . .
Завершает мою курсовую работу список используемой литературы, который состоит из девяти источников.
| 
|
группа
|
| 
|
порядок группы 
|
| 
|
класс всех разрешимых групп
|
| 
|
класс всех нильпотентных групп
|
| 
|
 является подгруппой группы является подгруппой группы 
|
| 
|
 является нормальной подгруппой группы является нормальной подгруппой группы 
|
| 
|
прямое произведение подгрупп  и и 
|
| 
|
подгруппа Фраттини группы 
|
| 
|
фактор-группа группы  по по 
|
| 
|
множество всех простых делителей натурального числа 
|
| 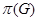
|
множество всех простых делителей порядка группы 
|
| 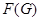
|
подгруппа Фиттинга группы 
|
| 
|
наибольшая инвариантная  -подгруппа группы -подгруппа группы 
|
| 
|
индекс подгруппы  в группе в группе 
|
 1. Введение.
Две работы (1) и (2), написанные Бернсайдом в 1904 г., посвящены конечным бипримарным группам - группам порядка 1. Введение.
Две работы (1) и (2), написанные Бернсайдом в 1904 г., посвящены конечным бипримарным группам - группам порядка 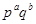 , ,  и и  - различные простые числа. В первой работе доказана разрешимость таких групп. Во второй - устанавливался следующий факт: в группе порядка - различные простые числа. В первой работе доказана разрешимость таких групп. Во второй - устанавливался следующий факт: в группе порядка 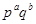 при при  существует характеристическая существует характеристическая  -подгруппа порядка -подгруппа порядка  , за исключением двух случаев , за исключением двух случаев  , ,  и и  , ,  . .
Однако группа  , являющаяся расширением элементарной абелевой группы , являющаяся расширением элементарной абелевой группы  порядка порядка  с помощью силовской с помощью силовской  -подгруппы из группы автоморфизмов группы -подгруппы из группы автоморфизмов группы  , имеет порядок , имеет порядок  , ,  и в и в  нет неединичных инвариантных нет неединичных инвариантных  -подгрупп. Этот пример указывает на то, что в работе имеется пробел. -подгрупп. Этот пример указывает на то, что в работе имеется пробел.
В настоящей работе рассматривается более общая ситуация, чем в . А именно, изучаются разрешимые группы порядка  , где , где  . Основным результатом является . Основным результатом является
Теорема
Пусть  - конечная разрешимая группа, порядка - конечная разрешимая группа, порядка  , ,  - простое число и - простое число и  не делит не делит  . Если . Если  , то либо , то либо  обладает характеристической обладает характеристической  -подгруппой порядка -подгруппой порядка  , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1)  , ,  и и  делит порядок делит порядок  ; ;
2)  , ,  делит порядок делит порядок  , где , где  - простое число, причем - простое число, причем  , если , если  , и , и  , если , если  ; ;
3)  , ,  1 и 1 и 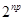 делит порядок делит порядок  . .
Если  и и  - различные простые числа, - различные простые числа,  и и  - целые положительные числа, то либо - целые положительные числа, то либо  , либо , либо  . Поэтому теорема распространяется па все бипримарные группы. . Поэтому теорема распространяется па все бипримарные группы.
Теорема
Пусть  - группа порядка - группа порядка 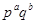 , ,  и и  - простые числа. Если - простые числа. Если  , то либо , то либо  обладает характеристической обладает характеристической  -подгруппой порядка -подгруппой порядка  , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1)  , ,  , ,  и и 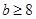 ; ;
2)  , ,  , , 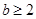 , причем , причем  , если , если  , и , и  , если , если  ; ;
3)  , ,  , ,  и и 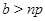 . .
Следствие
Если  и и 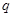 - нечетные простые числа и - нечетные простые числа и  , то любая группа порядка , то любая группа порядка 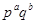 обладает характеристической обладает характеристической  -подгруппой порядка -подгруппой порядка  . .
Следующая теорема показывает, что границы, установленные для чисел 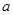 и и  , являются точными и что инвариантной , являются точными и что инвариантной  -подгруппы в исключительных случаях теорем (4) и (1) может и не быть. -подгруппы в исключительных случаях теорем (4) и (1) может и не быть.
Теорема
Группа порядка 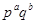 , ,  , не имеющая неединичных инвариантных , не имеющая неединичных инвариантных  -подгрупп, существует для каждого из следующих трех случаев: -подгрупп, существует для каждого из следующих трех случаев:
1)  , ,  , ,  и и  ; ;
2)  , ,  , ,  и и  , если , если  , , 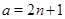 , если , если  ; ;
3)  , , 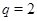 , , 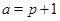 и и  . .
 2. Порядки силовских подгрупп полных линейных групп.
На множестве натуральных чисел введем следующую функцию: 2. Порядки силовских подгрупп полных линейных групп.
На множестве натуральных чисел введем следующую функцию:
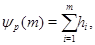
где  и и  взаимно просто с взаимно просто с  . Из определения вытекает, что . Из определения вытекает, что  есть показатель, с которым есть показатель, с которым  входит в произведение входит в произведение  . Поэтому . Поэтому

где 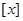 - целая часть числа - целая часть числа 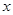 (см. ) и (см. ) и 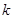 - наибольшее число, при котором - наибольшее число, при котором  . .
Тогда

Лемма
 . .
Лемма
Пусть 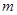 - показатель, которому - показатель, которому 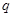 принадлежит по модулю принадлежит по модулю  , и пусть , и пусть  , ,  не делит не делит  . Тогда и только тогда . Тогда и только тогда  делит делит 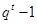 , когда , когда  кратно кратно 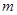 . Если . Если 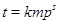 , ,  не делит не делит  , то, за исключением случая , то, за исключением случая  , число , число  есть наивысшая степень есть наивысшая степень  , которая делит , которая делит  . .
Доказательство. Первое утверждение вытекает из свойств показателей (см. (5)). Вычислим 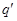 , используя бином Ньютона: , используя бином Ньютона:

Заметим, что

есть целое число. Действительно, 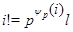 и число и число  делит произведение делит произведение  . Учитывая, что . Учитывая, что  , из леммы получаем, что , из леммы получаем, что 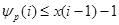 и и 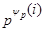 делит делит 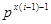 . Теперь . Теперь
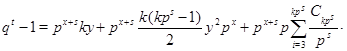

где  - целое число. Так как - целое число. Так как  не делит не делит 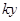 , то выражение в скобках не делится на , то выражение в скобках не делится на  , за исключением случая , за исключением случая  . Лемма доказана. . Лемма доказана.
Исключение  , в лемме существенно; легко заметить, что при , в лемме существенно; легко заметить, что при 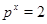 , ,  лемма неверна. Случай лемма неверна. Случай  был как раз и пропущен в рассуждениях работы (5). был как раз и пропущен в рассуждениях работы (5).
Лемма
Пусть  , ,  - нечетное число и - нечетное число и 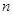 - наименьшее целое число, при котором - наименьшее целое число, при котором  . Пусть . Пусть 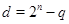 . Определим число . Определим число  так: если, так: если,  , то , то  . если . если  , тo , тo 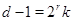  - нечетное число. Тогда - нечетное число. Тогда
1) если  - нечетное число, то - нечетное число, то  ; ;  ; ;
2) если  - четное число и - четное число и 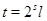 , ,  - нечетное число, то - нечетное число, то  , , 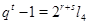 , где , где  , ,  , ,  и и  - нечетные числа. - нечетные числа.
Доказательство. Воспользуемся биномом Ньютона:

Если  - нечетное число, то - нечетное число, то

 - нечетное число. Если - нечетное число. Если  - четное число, то - четное число, то

 - нечетное число. - нечетное число.
Пусть теперь  - нечетное число - нечетное число  . Тогда . Тогда
 где где

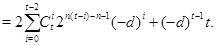
Ho 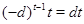 - нечетное число, поэтому - нечетное число, поэтому 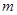 - нечетное число. Так как - нечетное число. Так как  , если , если  , и , и  , если , если  , то , то  , где , где  - нечетное число. - нечетное число.
И наконец, если 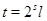 , , 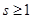 . .  - нечетное число, то - нечетное число, то
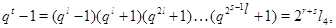
 - нечетное число. Лемма доказана. - нечетное число. Лемма доказана.
Лемма
Пусть  и и 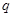 - различные простые числа, - различные простые числа, 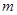 - показатель числа - показатель числа  по модулю по модулю  и и 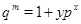 , ,  не делит не делит  . Пусть . Пусть  , ,  или или  и и  - порядок силовской - порядок силовской  -подгруппы группы -подгруппы группы 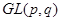 . Если . Если  , то , то  , где , где  - целое число, удовлетворяющее неравенству - целое число, удовлетворяющее неравенству 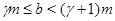 . Если . Если 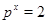 , то , то 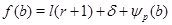 . Здесь число . Здесь число  определяется как и в лемме3. определяется как и в лемме3.
Доказательство. Порядок группы 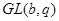 известен (см.2): известен (см.2):
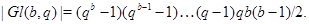
Ясно, что 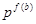 - наивысшая степень - наивысшая степень  , которая делит произведение , которая делит произведение 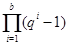 . .
Рассмотрим, вначале случай, когда  . Применяя лемму (3), заключаем, что в произведении . Применяя лемму (3), заключаем, что в произведении 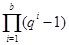 лишь следующие сомножители кратны лишь следующие сомножители кратны 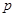 : :
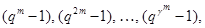
где 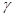 определяется неравенством определяется неравенством 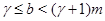 . Так как . Так как 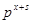 есть наивысшая степень есть наивысшая степень  , которая делит , которая делит  , где , где 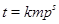 , ,  не делит не делит  , то наивысшая степень , то наивысшая степень  , которая делит , которая делит  , есть , есть 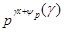 . .
Следовательно,
 . .
Пусть теперь  . Тогда . Тогда 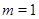 и и  . Заметим, что . Заметим, что

Применим индукцию по 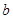 . Если . Если  , то , то 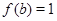 , а так как , а так как 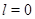 , ,  и и  , то утверждение для , то утверждение для 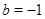 справедливо. справедливо.
Предположим, что равенство выполняется для 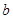 , и докажем его для , и докажем его для  . Пусть вначале . Пусть вначале  есть нечетное число, т.е. есть нечетное число, т.е. 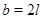 , ,  и и  . По лемме (4) . По лемме (4)  , , 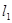 - нечетное число. Поэтому - нечетное число. Поэтому 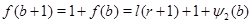 . Так как . Так как  , а , а  , то утверждение для , то утверждение для  справедливо. справедливо.
Пусть теперь  - четное число. Тогда - четное число. Тогда 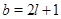 и и 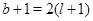 . Кроме того, если . Кроме того, если 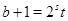 , , 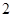 не делит не делит 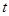 , то по лемме , то по лемме 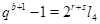 , ,  - нечетное число. Значит, - нечетное число. Значит,
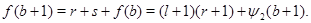
Лемма доказана полностью.
Лемма
Пусть  и и 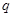 - различные простые числа и - различные простые числа и 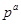 - порядок некоторой - порядок некоторой  -подгруппы группы -подгруппы группы 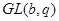 . Тогда либо . Тогда либо  , либо справедливо одно из следующих утверждении: , либо справедливо одно из следующих утверждении:
1)  , ,  , , 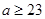 и и 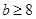 ; ;
2)  , ,  , , 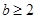 и и  , если , если  , , 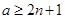 , если , если  ; ;
3)  , , 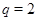 , ,  , и , и 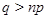 . .
Доказательство. Пусть  - показатель числа - показатель числа 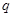 по модулю по модулю  и и 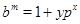 , ,  не делит не делит 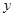 . Так как . Так как  - порядок силовской - порядок силовской  -подгруппы группы -подгруппы группы 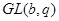 , то , то  . Если . Если  , то лемма справедлива. Поэтому пусть в дальнейшем , то лемма справедлива. Поэтому пусть в дальнейшем 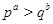 . Рассмотрим вначале случай, когда . Рассмотрим вначале случай, когда 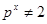 . По лемме в этом случае . По лемме в этом случае 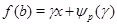 , где , где  определяется неравенством определяется неравенством 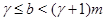 . Допустим, что . Допустим, что  . Так как . Так как 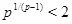 , то , то  и и 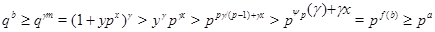 - противоречие. Значит, - противоречие. Значит,  , поэтому либо , поэтому либо  , либо , либо 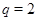 . .
Пусть  . Тогда . Тогда 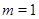 , а так как , а так как 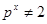 , то , то  и и 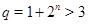 . Если . Если  , то , то  и и  - противоречие. Если - противоречие. Если 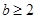 , то , то  . Кроме того, . Кроме того,  . Поэтому из условия . Поэтому из условия  следует, что следует, что 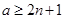 . Получили утверждение для . Получили утверждение для  из пункта 2. из пункта 2.
Теперь пусть 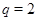 . Тогда . Тогда 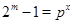 . Легко показать, что . Легко показать, что  , поэтому , поэтому 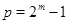 . Если . Если 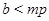 , то , то 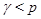 и и 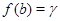 . Отсюда следует, что . Отсюда следует, что
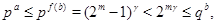
получили противоречие. Значит,  , т.е. , т.е.  и и  . Поэтому . Поэтому  . Воспользуемся неравенством . Воспользуемся неравенством 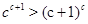 , которое справедливо при , которое справедливо при  . Тогда . Тогда
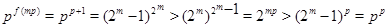
и из  следует, что следует, что  и и  . Получили утверждение из пункта 3. Случай . Получили утверждение из пункта 3. Случай 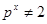 разобран полностью. разобран полностью.
Рассмотрим теперь случай 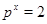 . Тогда . Тогда  . Пусть . Пусть  - наименьшее целое число, при котором - наименьшее целое число, при котором  , и пусть , и пусть  . Предположим, что . Предположим, что  . Тогда . Тогда  . Но . Но 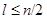 и и 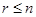 , поэтому , поэтому 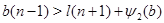 и и 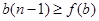 . Если . Если 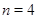 , то , то 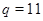 , ,  и и  . Кроме того, . Кроме того,  . Отсюда . Отсюда 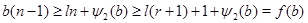 . Следовательно, при . Следовательно, при 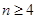 справедливо неравенство справедливо неравенство 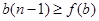 . Так как . Так как 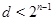 , то , то  и и 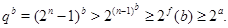
Таким образом, при 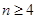 всегда всегда  . Значит, надо рассмотреть лишь два случая: . Значит, надо рассмотреть лишь два случая:  и и  . .
Пусть  , тогда , тогда  . Непосредственно проверяется, что . Непосредственно проверяется, что 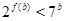 при при 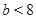 . При . При 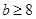 имеем имеем 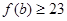 , причем , причем  . Поэтому . Поэтому 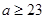 . Получили утверждение из пункта 1. . Получили утверждение из пункта 1.
Осталось рассмотреть  . Теперь . Теперь 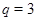 . В . В  силовская силовская  -подгруппа имеет порядок -подгруппа имеет порядок  . Так как . Так как 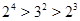 , то , то 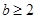 и и  . Но . Но  , ,  . Поэтому этот случай записан в пункте 2. Лемма доказана полностью. . Поэтому этот случай записан в пункте 2. Лемма доказана полностью.
Доказательство теоремы . Пусть  , , 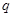 - упорядоченная пара простых чисел, - упорядоченная пара простых чисел, 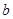 - натуральное число и - натуральное число и  , , 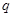 , , 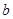 удовлетворяют одному из трех требований теоремы. Через удовлетворяют одному из трех требований теоремы. Через  обозначим элементарную абелеву группу порядка обозначим элементарную абелеву группу порядка  , через , через  - силовскую - силовскую  -подгруппу группы -подгруппу группы 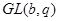 . Так как . Так как 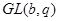 есть группа автоморфизмов группы есть группа автоморфизмов группы 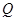 , то группа , то группа  , являющаяся расширением группы , являющаяся расширением группы  с помощью группы с помощью группы  , не имеет инвариантных , не имеет инвариантных  -подгрупп -подгрупп  . Покажем, что . Покажем, что  - искомая группа. Вычислим порядок группы - искомая группа. Вычислим порядок группы  . Из леммы следует, что . Из леммы следует, что  причем: причем:
1)  , если , если 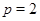 и и 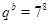 ; ;
2)  , если , если 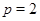 , ,  и и 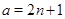 , если , если 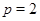 , ,  , ,  ; ;
3) 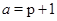 , если , если  , , 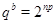 . .
В первых двух случаях непосредственно проверяется, что  . Используя неравенство . Используя неравенство  , которое справедливо при , которое справедливо при 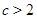 , в третьем случае получаем , в третьем случае получаем 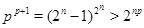 . Таким образом, . Таким образом,  и в каждом из трех случаев и в каждом из трех случаев  . Теорема доказана. . Теорема доказана.
 3. Доказательство теоремы
.
Допустим, что теорема неверна и группа 3. Доказательство теоремы
.
Допустим, что теорема неверна и группа  - контрпример минимального порядка. Пусть - контрпример минимального порядка. Пусть  - силовская - силовская  -подгруппа, -подгруппа,  - силовское - силовское  -дополнение в -дополнение в 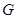 . .
Обозначим через 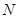 наибольшую инвариантную наибольшую инвариантную  -подгруппу из -подгруппу из  . Подгруппа . Подгруппа 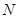 характеристическая и характеристическая и 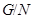 не имеет неединичных инвариантных не имеет неединичных инвариантных  -подгрупп. Предположим, что -подгрупп. Предположим, что 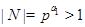 . Факторгруппа . Факторгруппа 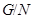 имеет порядок имеет порядок 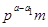 . Если . Если  , то , то  - противоречие. Поэтому - противоречие. Поэтому  и для и для  выполняется одно из утверждений пунктов 1 - 3 заключения теоремы. Но тогда это утверждение выполняется и для выполняется одно из утверждений пунктов 1 - 3 заключения теоремы. Но тогда это утверждение выполняется и для 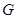 - противоречие. Следовательно, в - противоречие. Следовательно, в  нет неединичных инвариантных нет неединичных инвариантных  -подгрупп. -подгрупп.
Пусть  - подгруппа Фиттинга группы - подгруппа Фиттинга группы 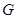 . Так как . Так как  разрешима, то разрешима, то 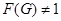 . Ясно, что . Ясно, что 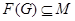 . Если . Если 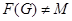 , то , то 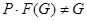 и группа и группа 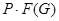 удовлетворяет условию теоремы. Но для удовлетворяет условию теоремы. Но для 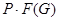 не выполняется ни одно из утверждений пунктов 1 - 3 заключения теоремы, иначе оно выполнялось бы и для не выполняется ни одно из утверждений пунктов 1 - 3 заключения теоремы, иначе оно выполнялось бы и для  . Поэтому группа . Поэтому группа  обладает неединичной инвариантной обладает неединичной инвариантной  -подгруппой -подгруппой  . Теперь . Теперь  централизует централизует 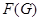 , а это противоречит теореме о том, что в разрешимых группах подгруппа Фиттинга содержит свой централизатор (см. ). Таким образом, , а это противоречит теореме о том, что в разрешимых группах подгруппа Фиттинга содержит свой централизатор (см. ). Таким образом, 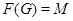 . .
Допустим, что подгруппа Фраттини 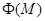 группы группы  неединична. Тогда факторгруппа неединична. Тогда факторгруппа  удовлетворяет условию теоремы. Если в удовлетворяет условию теоремы. Если в 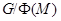 имеется неединичная инвариантная имеется неединичная инвариантная  -подгруппа -подгруппа  , то по теореме Гашюца группа , то по теореме Гашюца группа  нильпотентна и нильпотентна и 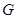 обладает инвариантной обладает инвариантной  -подгруппой -подгруппой 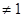 - противоречие. Но для - противоречие. Но для  не выполняется ни одно из утверждений пунктов 1 - 3. Следовательно, не выполняется ни одно из утверждений пунктов 1 - 3. Следовательно, 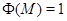 и все силовские в и все силовские в 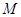 подгруппы элементарные абелевы. подгруппы элементарные абелевы.
Пусть  , ,  - силовская подгруппа группы - силовская подгруппа группы  . Тогда группа автоморфизмов . Тогда группа автоморфизмов 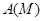 группы группы 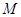 является прямым произведением групп является прямым произведением групп 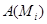 (см. ). Так как (см. ). Так как 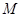 совпадает со своим централизатором в совпадает со своим централизатором в 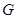 , то , то  изоморфна некоторой изоморфна некоторой  -подгруппе из -подгруппе из 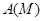 . Но силовская . Но силовская  -подгруппа из -подгруппа из 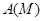 имеет вид имеет вид  , где , где 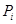 - некоторая силовская - некоторая силовская  -подгруппа из -подгруппа из 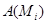 (см. ). Поэтому (см. ). Поэтому  изоморфна некоторой подгруппе из изоморфна некоторой подгруппе из 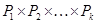 . По условию теоремы . По условию теоремы 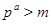 , поэтому существует номер , поэтому существует номер 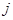 такой, что такой, что  . .
Если  , то , то 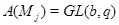 и и  , есть силовская , есть силовская  -подгруппа группы -подгруппа группы  . Применяя лемму , заключаем, что . Применяя лемму , заключаем, что 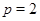 , ,  и и 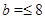 или или 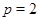 , ,  и и 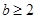 , или , или  , , 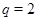 и и 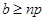 . Используя условие . Используя условие 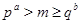 , нетрудно получить соответствующие оценки для числа , нетрудно получить соответствующие оценки для числа  . Теорема доказана. . Теорема доказана.
 4. Пример.
В 1969 г.Г.Я. Мордкович на Гомельском алгебраическом семинаре С.А. Чунихина высказал предположение: в группе порядка 4. Пример.
В 1969 г.Г.Я. Мордкович на Гомельском алгебраическом семинаре С.А. Чунихина высказал предположение: в группе порядка 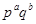 при при 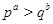 либо силовская либо силовская  -подгруппа инвариантна, либо существует неединичная инвариантная -подгруппа инвариантна, либо существует неединичная инвариантная  -подгруппа. Мы построим пример, опровергающий это предположение. -подгруппа. Мы построим пример, опровергающий это предположение.
Напомним, что 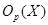 означает наибольшую инвариантную означает наибольшую инвариантную  -подгруппу группы -подгруппу группы  . Группа . Группа  называется называется  -замкнутой, если в ней силовская -замкнутой, если в ней силовская  -подгруппа инвариантна. -подгруппа инвариантна.
Лемма
Пусть 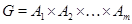 , где , где 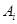 - подгруппа группы - подгруппа группы  , , 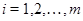 . Если . Если  для всех для всех  , то , то  . .
Доказательство проведем индукцией по  . Для . Для 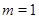 лемма справедлива. Пусть утверждение верно для лемма справедлива. Пусть утверждение верно для 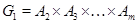 и и 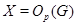 . Так как . Так как  и и 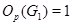 , то , то 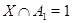 и и 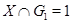 . Теперь . Теперь  . Отсюда следует, что . Отсюда следует, что 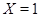 . Лемма доказана. . Лемма доказана.
Нам потребуется следующая конструкция Л.А. Шеметкова (см. ).
Лемма Л.А. Шеметков
Для любой упорядоченной пары  , , 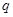 различных простых чисел существует группа различных простых чисел существует группа 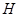 порядка порядка 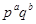 со следующими свойствами: со следующими свойствами:
1)  , , 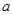 - показатель, которому принадлежит - показатель, которому принадлежит  по модулю по модулю 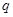 ; ;
2) 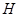 не не 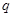 -замкнута, силовская -замкнута, силовская 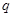 -подгруппа из -подгруппа из 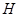 максимальна в максимальна в 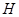 и и  . .
Предположение
Для каждого из следующих трех случаев
1) 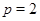 , , 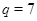 ; ;
2) 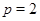 , ,  ; ;
3) 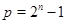 , , 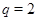 существует не существует не 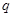 -замкнутая группа -замкнутая группа  порядка порядка 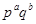 , причем , причем  и и 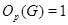 . .
Доказательство. Пусть  , , 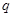 - упорядоченная пара простых чисел, удовлетворяющая одному из требований предложения . Пусть - упорядоченная пара простых чисел, удовлетворяющая одному из требований предложения . Пусть 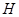 - -  -группа из леммы с максимальной силовской -группа из леммы с максимальной силовской 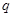 -подгруппой, -подгруппой,  - -  -группа, построенная в теореме , с инвариантной силовской -группа, построенная в теореме , с инвариантной силовской 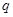 -подгруппой и -подгруппой и 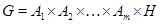 , где , где 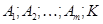 . Так как . Так как 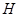 не не 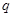 -замкнута, то и -замкнута, то и 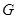 не не 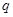 -замкнута. Кроме того, -замкнута. Кроме того,  и и  , ,  . Поэтому, . Поэтому,  по лемме . Осталось показать, что в каждом из трех случаев натуральное число по лемме . Осталось показать, что в каждом из трех случаев натуральное число 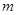 можно задать так, что группа можно задать так, что группа 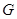 будет иметь порядок будет иметь порядок 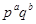 , причем , причем  . .
Пусть 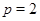 , , 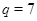 . Тогда . Тогда 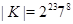 , а , а 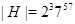 . Если . Если 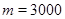 , то , то 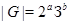 , где , где 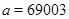 , , 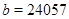 . Нетрудно проверить, что . Нетрудно проверить, что  . .
Пусть теперь 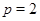 , ,  . Предположим, что . Предположим, что  . Тогда . Тогда  , ,  и и  , где , где  , a , a  . Если в качестве . Если в качестве  выбрать натуральное число, удовлетворяющее неравенству: выбрать натуральное число, удовлетворяющее неравенству: 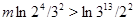 , то , то  . Допустим теперь, что . Допустим теперь, что 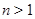 . Тогда . Тогда 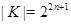 , ,  и и  , где , где 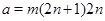 , , 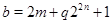 . Так как . Так как 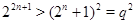 , то существует натуральное число , то существует натуральное число 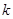 , удовлетворяющее неравенству , удовлетворяющее неравенству 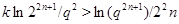 . Если положить . Если положить  , то , то  . .
Наконец, пусть  , , 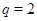 . Тогда . Тогда 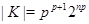 , , 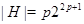 и и 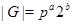 , где , где  , , 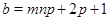 . Теперь в качестве . Теперь в качестве  надо выбрать натуральное число, удовлетворяющее неравенству надо выбрать натуральное число, удовлетворяющее неравенству  . Тогда . Тогда  . Предположение доказано. . Предположение доказано.
В заметке (1) исправлена ошибка, допущенная Бернсайдом в работе (2). А именно в (3) доказано, что группа 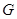 порядка порядка 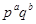 , где , где  и и 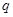 - различные простые числа и - различные простые числа и 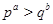 , либо обладает характеристической , либо обладает характеристической  -подгруппой порядка -подгруппой порядка  , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1) 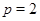 , ,  , , 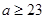 и и 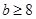 ; ;
2) 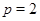 , ,  , , 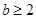 и и 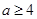 , если , если  , , 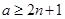 , если , если 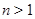 ; ;
3)  , , 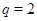 , ,  и и 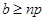 . .
Доказательство этого результата сводится к случаю, когда силовская 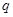 -подгруппа из -подгруппа из 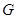 является минимальной инвариантной подгруппой, совпадающей со своим централизатором. В этом случае силовская является минимальной инвариантной подгруппой, совпадающей со своим централизатором. В этом случае силовская 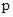 - подгруппа из - подгруппа из 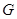 изоморфно вкладывается в общую линейную группу изоморфно вкладывается в общую линейную группу 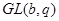 и возникает необходимость сравнить порядок силовской и возникает необходимость сравнить порядок силовской  -подгруппы из -подгруппы из 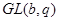 с числом с числом 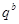 . В лемме 2.5 из указывались значения . В лемме 2.5 из указывались значения  , , 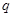 и нижняя граница для числа и нижняя граница для числа  , при которых порядок силовской , при которых порядок силовской 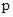 - подгруппы из - подгруппы из 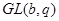 больше больше  . .
Цель настоящей заметки - указать все значения чисел  , , 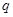 и и  , при которых силовская , при которых силовская 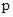 -подгруппа из -подгруппа из  имеет порядок больший, чем имеет порядок больший, чем 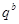 . .
Теорема
Пусть  и и 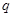 - различные простые числа и - различные простые числа и  - порядок силовской - порядок силовской  -подгруппы из группы -подгруппы из группы 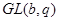 . Тогда и только тогда . Тогда и только тогда 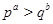 , когда выполняется одно из условий: , когда выполняется одно из условий:
1)  , , 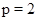 , ,  - любое натуральное число за исключением - любое натуральное число за исключением 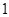 , ,  , , 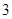 , ,  , ,  , , 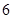 , ,  , , 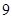 , , 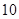 , , 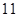 , , 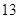 , , 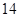 , ,  , , 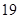 , , 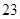 , ,  ; ;
2)  , , 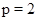 , ,  - любое натуральное число - любое натуральное число 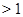 ; ;
3) 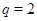 , ,  , ,  - любое натуральное число - любое натуральное число  за исключением за исключением 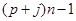 , где , где 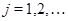 ; ;  , где , где 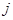 - любое целое число, удовлетворяющее неравенству - любое целое число, удовлетворяющее неравенству  . Для . Для 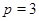 дополнительно исключаются числа дополнительно исключаются числа 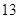 , ,  , ,  и и 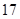 ; для ; для  дополнительно исключаются дополнительно исключаются 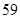 и и  . .
Доказательство теоремы основывается на формуле для вычисления порядка силовской 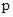 -подгруппы общей линейной группы -подгруппы общей линейной группы 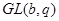 , полученной в . , полученной в .
Пусть  и и 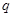 - различные простые числа, - различные простые числа,  - показатель числа - показатель числа 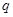 по модулю по модулю  и и 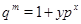 , , 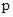 не делит не делит 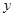 . Через . Через 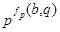 обозначим порядок силовской обозначим порядок силовской 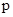 -подгруппы группы -подгруппы группы 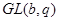 , а через , а через 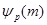 - показатель, с которым - показатель, с которым  входит в произведение входит в произведение  . В доказана следующая . В доказана следующая
Лемма
Если 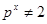 , то , то 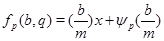 . Если . Если 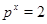 , то , то 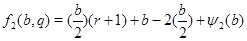 и число и число 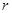 определяется так: пусть определяется так: пусть  - наименьшее целое, при котором - наименьшее целое, при котором 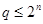 и и  ; если ; если 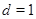 , то , то  ; если ; если 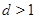 , то , то 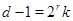 , , 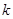 - нечетное число. - нечетное число.
Напомним, что 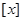 - целая часть числа - целая часть числа 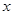 , т.е. наибольшее целое число, не превосходящее , т.е. наибольшее целое число, не превосходящее 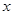 (см. ). (см. ).
Лемма
Если  - натуральное число, то - натуральное число, то
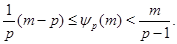
Доказательство. Пусть 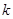 - наибольшее целое число, при котором - наибольшее целое число, при котором  . Так как . Так как 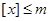 , то , то
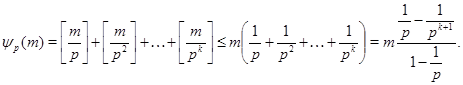
С другой стороны,
 и и 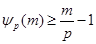 . .
Лемма
Если  - натуральное число - натуральное число 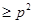 , то , то  . .
Доказательство проводим индукцией по  . Если . Если 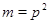 , то , то
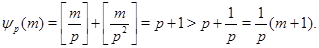
Пусть утверждение верно для  . Докажем его для . Докажем его для  . .
Если  кратно кратно 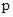 , то , то
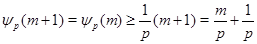 . Но . Но 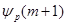 - целое число, а - целое число, а  - -
дробное. Поэтому

Если  кратно кратно 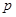 , то , то 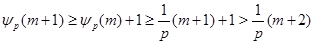 . .
Пусть, наконец, оба числа 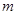 и и  не кратны не кратны 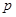 , тогда , тогда 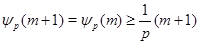 , причем , причем 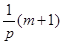 не целое число. Так как число не целое число. Так как число 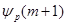 целое, то целое, то  , откуда , откуда 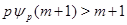 . Лемма доказана. . Лемма доказана.
Лемма
Если  - натуральное число, а - натуральное число, а 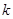 - наибольшее целое число, при котором - наибольшее целое число, при котором 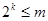 , то , то 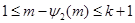 . .
Доказательство. По лемме , 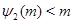 , поэтому , поэтому  . Неравенство . Неравенство 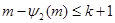 докажем индукцией по докажем индукцией по  . Для . Для 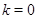 и и 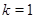 справедливость неравенства проверяется непосредственно. справедливость неравенства проверяется непосредственно.
Пусть 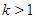 и пусть это неравенство верно для всех и пусть это неравенство верно для всех  . Докажем его для . Докажем его для  . Разность . Разность  обозначим через обозначим через  . Так как . Так как  , то , то  . Поэтому если . Поэтому если 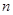 - наибольшее целое число, при котором, - наибольшее целое число, при котором,  , то , то  и по индукции имеем и по индукции имеем 
Вычислим  . Так как . Так как
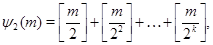
то

Лемма доказана.
Замечание. Границы, указанные в лемме , точные. Левая граница достигается при 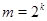 , правая - при , правая - при  . .
Лемма
Если натуральное число  , то , то 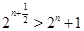 и и 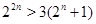 . .
Доказательство обоих неравенств легко получить индукцией по 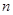 . .
Доказательство теоремы 3. Сохраним все обозначения леммы . Рассмотрим вначале случай, когда 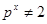 . По лемме (5), в этом случае . По лемме (5), в этом случае 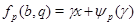 , где , где 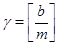 . Допустим, что . Допустим, что 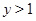 . Так как . Так как 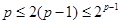 , то , то 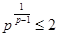 и и 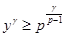 . Поэтому . Поэтому 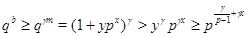 , и, применяя лемму , получаем , и, применяя лемму , получаем 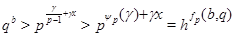 , что противоречит условию теоремы. , что противоречит условию теоремы.
Значит, 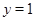 , поэтому либо , поэтому либо 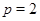 , либо , либо 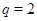 . .
Пусть  . Тогда . Тогда 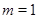 , а так как , а так как 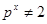 , то , то 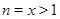 и и 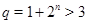 . .
Пусть 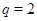 . Тогда . Тогда 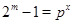 . Если . Если 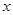 четное, то четное, то 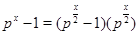 , т.е.4 делит , т.е.4 делит 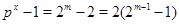 . Противоречие. Значит, . Противоречие. Значит, 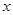 нечетное. Поэтому нечетное. Поэтому  , и так как число , и так как число  нечетное, то нечетное, то 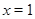 . Таким образом, если . Таким образом, если 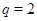 , то , то  . .
Итак, если 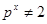 , то либо , то либо  и и  , либо , либо 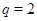 и и 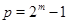 . .
Пусть  . Тогда из леммы следует, что . Тогда из леммы следует, что
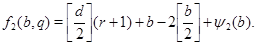
Предположим, что 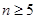 . Тогда . Тогда 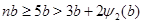 (см. лемму ), а так как при (см. лемму ), а так как при 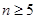 справедливо неравенство справедливо неравенство 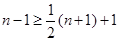 , то , то 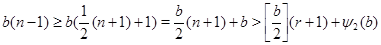 . Учитывая, что . Учитывая, что  или или 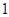 , получаем , получаем  . .
Если 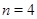 , то , то 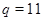 и и 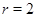 . Кроме того, . Кроме того,  , поэтому , поэтому
 и и 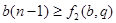 . .
Таким образом, при  выполняется неравенство выполняется неравенство 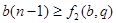 . Так как . Так как 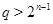 , то , то 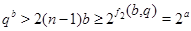 . Противоречие с условием теоремы. . Противоречие с условием теоремы.
Следовательно, 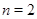 или или 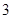 и и 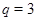 или или 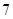 . .
Итак, нам необходимо рассмотреть следующие случаи: 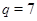 , , 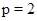 ; ; 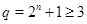 , , 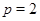 ; ; 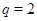 , ,  . .
Случай 1. Пусть  , , 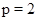 . В этом случае . В этом случае

Если 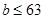 , то, вычисляя , то, вычисляя 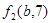 для каждого значения для каждого значения 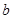 с помощью натуральных логарифмов, убеждаемся; что с помощью натуральных логарифмов, убеждаемся; что 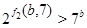 в точности для следующих в точности для следующих  , , 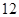 , , 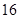 , ,  , , 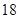 , ,  , , 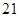 , ,  , , 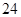 -- -- , , 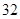 -- --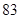 . .
Пусть 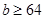 и и  - наибольшее натуральное число, при котором - наибольшее натуральное число, при котором 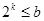 . Ясно, что . Ясно, что  . С помощью индукции легко проверяется неравенство; . С помощью индукции легко проверяется неравенство;  . Используя лемму , мы получаем: . Используя лемму , мы получаем:

Теперь
 Таким образом, Таким образом, 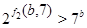 . .
Случай 2. Пусть  , , 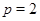 . В этом случае . В этом случае 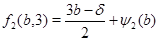 , где , где  , если , если 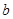 четное, и четное, и 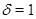 если если 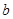 нечетное, а нечетное, а 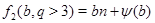 . Если . Если 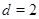 или 3, а или 3, а 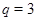 , то непосредственно убеждаемся, что , то непосредственно убеждаемся, что 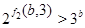 . Если . Если 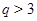 , то , то 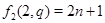 , а , а 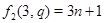 и и  т.е. т.е. 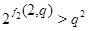 . Используя лемму , получаем . Используя лемму , получаем
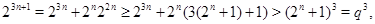 т.е. т.е.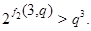
Теперь пусть 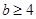 . Из леммы имеем . Из леммы имеем 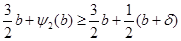 или или 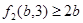 . Поэтому . Поэтому 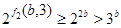 . Осталось рассмотреть случай, когда . Осталось рассмотреть случай, когда 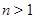 . Тогда . Тогда  , поэтому, используя леммы и , получаем: , поэтому, используя леммы и , получаем:

Таким образом, при любом  имеет место неравенство имеет место неравенство  . .
Случай 3. Пусть 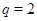 , , 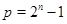 . В этом случае . В этом случае 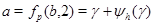 , где , где 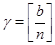 - целая часть числа - целая часть числа  . Если . Если  , то , то 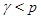 и и  . Отсюда следует, что . Отсюда следует, что  . Противоречие. Значит, . Противоречие. Значит,  и и  . Мы можем записать . Мы можем записать 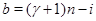 , , 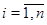 . .
Рассмотрим вначале случай, когда 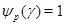 , т.е. когда , т.е. когда 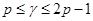 . .
Тогда 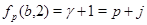 , , 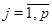 . .
Если 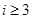 , то , то  , где , где  - основание натуральных логарифмов и - основание натуральных логарифмов и
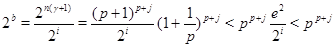 , т.е. , т.е. 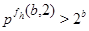 . .
Если 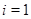 , то , то 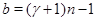 и и 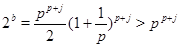 , т.е. , т.е. 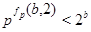 . Найдем значения . Найдем значения 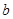 для для 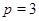 и и 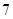 . Для . Для 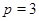 имеем: имеем:

Для 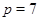 имеем: имеем:

Если 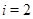 , то , то  , и при , и при 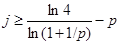 получаем получаем
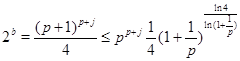 , т.е. , т.е. 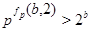 . .
Если 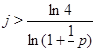 , то , то  . Определим для . Определим для 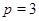 и и 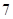 значения значения 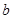 , при которых , при которых 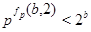 . Для . Для 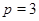 имеем имеем 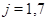 , т.е. , т.е.  , а , а 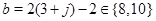 . Для . Для  имеем имеем 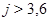 , т.е. , т.е. 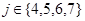 , а , а  . .
Теперь рассмотрим случай, когда 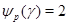 , т.е. когда , т.е. когда  . .
Если 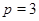 , то , то  и и 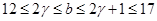 . Непосредственно убеждаемся, что лишь при . Непосредственно убеждаемся, что лишь при 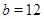 или или  имеет место неравенство имеет место неравенство 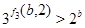 . .
Если 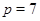 , то , то 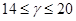 и и 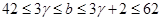 . Непосредственно убеждаемся, что лишь только при . Непосредственно убеждаемся, что лишь только при 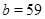 и и  имеет место неравенство имеет место неравенство 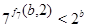 . .
Пусть 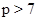 . Так как . Так как 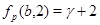 , a , a  , то , то
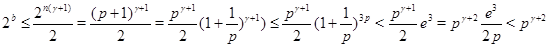 , ,
так как 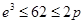 . .
Таким образом, 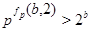 . .
Пусть теперь  . Тогда . Тогда 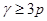 . Пусть вначале . Пусть вначале 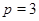 . Тогда . Тогда  , и по лемме 3 имеем , и по лемме 3 имеем 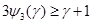 . Поэтому . Поэтому
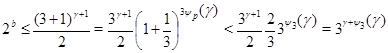
Здесь мы воспользовались неравенством  , которое вытекает из неравенства , которое вытекает из неравенства  . Таким образом, доказано, что . Таким образом, доказано, что 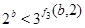 . .
Остался случай 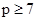 . Так как . Так как 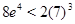 , то , то
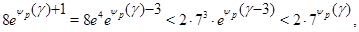
и, применяя лемму , получаем

Таким образом, 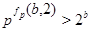 . .
Теорема доказана.
Итак, в данной курсовой работе исследовано существование примарных нормальных подгрупп в бипримарных группах. Также изучены и доказаны следующие основные теоремы:
Теорема. Пусть 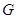 - конечная разрешимая группа, порядка - конечная разрешимая группа, порядка  , ,  - простое число и - простое число и 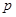 не делит не делит  . Если . Если 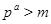 , то либо , то либо 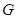 обладает характеристической обладает характеристической  -подгруппой порядка -подгруппой порядка 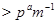 , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1) 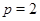 , , 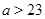 и и 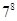 делит порядок делит порядок 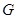 ; ;
2) 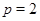 , , 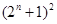 делит порядок делит порядок  , где , где 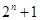 - простое число, причем - простое число, причем 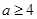 , если , если 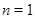 , и , и  , если , если  ; ;
3) 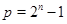 , , 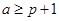 1 и 1 и 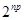 делит порядок делит порядок 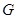 . .
Теорема. Пусть 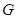 - группа порядка - группа порядка  , , 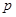 и и 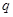 - простые числа. Если - простые числа. Если  , то либо , то либо 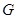 обладает характеристической обладает характеристической 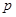 -подгруппой порядка -подгруппой порядка  , либо справедливо одно из следующих утверждений: , либо справедливо одно из следующих утверждений:
1) 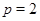 , , 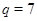 , ,  и и 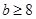 ; ;
2) 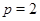 , , 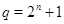 , , 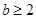 , причем , причем 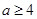 , если , если  , и , и 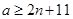 , если , если 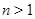 ; ;
3) 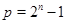 , , 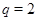 , , 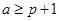 и и 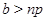 . .
Теорема.
Группа порядка 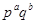 , , 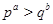 , не имеющая неединичных инвариантных , не имеющая неединичных инвариантных 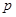 -подгрупп, существует для каждого из следующих трех случаев: -подгрупп, существует для каждого из следующих трех случаев:
1)  , , 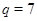 , ,  и и 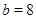 ; ;
2) 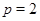 , , 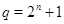 , ,  и и 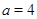 , если , если 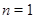 , , 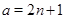 , если , если  ; ;
3) 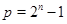 , , 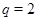 , , 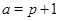 и и 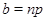 . .
Теорема. Пусть 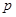 и и 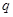 - различные простые числа и - различные простые числа и 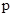 - порядок силовской - порядок силовской  -подгруппы из группы -подгруппы из группы 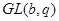 . Тогда и только . Тогда и только  , когда выполняется одно из условий: , когда выполняется одно из условий:
1) 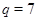 , , 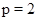 , ,  - любое натуральное число за исключением - любое натуральное число за исключением 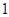 , , 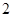 , , 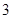 , , 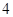 , , 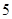 , , 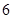 , ,  , ,  , , 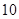 , , 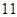 , ,  , ,  , , 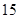 , ,  , , 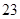 , , 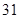 ; ;
2) 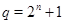 , , 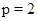 , ,  - любое натуральное число - любое натуральное число 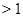 ; ;
3) 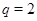 , , 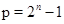 , ,  - любое натуральное число - любое натуральное число 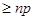 за исключением за исключением 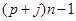 , где , где 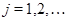 ; ; 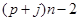 , где , где 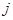 - любое целое число, удовлетворяющее неравенству - любое целое число, удовлетворяющее неравенству 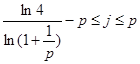 . Для . Для 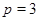 дополнительно исключаются числа дополнительно исключаются числа 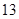 , , 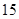 , ,  и и 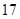 ; для ; для 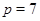 дополнительно исключаются дополнительно исключаются 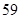 и и 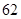 . .
Burnside W., On groups of order 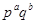 , Proc. London Math. Soc.2, № 1 (1904), 388--392. , Proc. London Math. Soc.2, № 1 (1904), 388--392.
Вurnside W., On groups of order 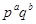 (Second paper), Proc. London Math. Soc., 2, № 2 (1905), 432--437. (Second paper), Proc. London Math. Soc., 2, № 2 (1905), 432--437.
Вurnside W., Theory of groups of finite order, Cambridge, 1911.
Виноградов И.М., Основы теории чисел, М., Наука, 1965.
Huppert В., Endliche Gruppen. I, Berlin, Springer, 1967.
Шеметков Л.А., К теореме Д.К. Фаддеева о конечных разрешимых группах, Матем. заметки, 5, № 6 (1969), 665--668.
Монахов В.С., Инвариантные подгруппы бипримарных групп. Матем. заметки, 18, № 6 (1975) б 877-886.
Burnside W., On groups of order 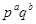 (second paper), Proc. London Math. Soc., 2, N 2 (1905), 432--437. (second paper), Proc. London Math. Soc., 2, N 2 (1905), 432--437.
Виноградов И.М., Основы теории чисел, М., 1965.
|