|
Рассмотрим две задачи Циолковского: прямолинейное движение точки переменной массы под действием только одной реактивной силы и вертикальное движение точки вблизи Земли в однородном поле силы тяжести. Эти задачи впервые рассматривались К. Э. Циолковским.
Первая задача Циолковского
Пусть точка переменной массы или ракета движется прямолинейно в таком называемом, по терминологии Циолковского, свободном пространстве под действием только одной реактивной силы. Считаем, что относительная скорость 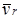 , отделения частиц постоянна и направлена в сторону, противоположную скорости , отделения частиц постоянна и направлена в сторону, противоположную скорости  движения точки переменной массы (рис. 1). Тогда, проецируя на ось Ох
, направленную по скорости движения точки, дифференциальное уравнение прямолинейного движения точки переменной массы принимает вид движения точки переменной массы (рис. 1). Тогда, проецируя на ось Ох
, направленную по скорости движения точки, дифференциальное уравнение прямолинейного движения точки переменной массы принимает вид
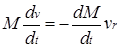 . .
Разделяя переменные и беря интегралы от обеих частей, имеем
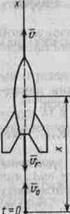
Рис. 1
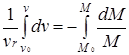 , ,
где 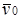 —
начальная скорость, направленная по реактивной силе; —
начальная скорость, направленная по реактивной силе;  —
начальная масса точки. —
начальная масса точки.
Выполняя интегрирование, получаем
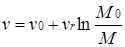 . (14) . (14)
Если в формулу (14) подставить значения величин, характеризующих конец горения, когда масса точки (ракеты) состоит только из массы несгоревшей части (массы приборов и корпуса ракеты)  , то, обозначая через т
массу топлива, для скорости движения v
1 в конце горения имеем , то, обозначая через т
массу топлива, для скорости движения v
1 в конце горения имеем
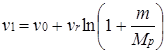 . .
Вводя ч и с л о Ц и о л к о в с к о г о Z==m/
M
p
, получаем следующую формулу Циолковского:
 . (15) . (15)
Из формулы Циолковского следует, что скорость в конце горения не зависит от закона горения, т. е. закона изменения массы.
Скорость в конце горения можно увеличить двумя путями. Одним из этих путей является увеличение относительной скорости отделения частиц  или для ракеты увеличения скорости истечения газа из сопла реактивного двигателя. или для ракеты увеличения скорости истечения газа из сопла реактивного двигателя.
Современные химические топлива позволяют получать скорости истечения газа из сопла реактивного двигателя порядка 2...2,3 км/с. Создание ионного и фотонного двигателей позволит значительно увеличить эту скорость. Другой путь увеличения скорости ракеты в конце горения связан с увеличением так называемой массовой, или весовой, отдачи ракеты, т. е. с увеличением числа Z, что достигается рациональной конструкцией ракеты. Можно значительно увеличить массовую отдачу ракеты М
0/М
р путем применения м н о г о с т у п е н ч а т о й ракеты, у которой после израсходования топлива первой ступени отбрасываются баки и двигатели от оставшейся части ракеты. Так происходит со всеми баками и двигателями уже отработавших ступеней ракеты. Это значительно повышает число Циолковского для каждой последующей ступени, так как уменьшается М
р
за счет отброшенных масс баков и двигателей.
Для определения уравнения движения точки переменной массы из (14) имеем
 , ,
или, выполняя интегрирование после разделения переменных и считая х=
0 при t
=0, получаем
 . (16) . (16)
В теоретических работах по ракетодинамике обычно рассматривают два закона изменения массы: линейный и показательный. При линейном законе масса точки с течением времени изменяется так:
M=M
0
(1-
a
t),
(17)
где a=const (a—удельный расход), а М
0—
масса точки в начальный момент времени.
При показательном законе изменение массы
 . (18) . (18)
Выполняя интегрирование в (16) при линейном законе изменения массы (17), получаем следующее уравнение движения:
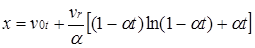 . (19) . (19)
При показательном законе изменения массы (18) соответственно
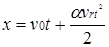 . (20) . (20)
Отметим, что при линейном законе изменения массы (17), если  =const, секундный расход массы =const, секундный расход массы
(- dM
/dt
) =aM
0 = const
и реактивная сила
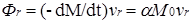 = const. = const.
При показательном законе секундный расход массы и реактивная сила являются переменными, но ускорение точки переменной массы  , вызванное действием на точку одной реактивной силы , вызванное действием на точку одной реактивной силы  , является постоянным, т. е. , является постоянным, т. е.
 =const. =const.
|