|
17. Турбулентный режим течения. Основные св-ва потока. Структура потока
для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измернть и записать пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис. 1.54. Скорость беспорядочно колеблется около некоторого осреднепного у0
ср п0
, времени значения, которое в данном случае остается постоянным!
Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рис. 1.55). Таким образом^
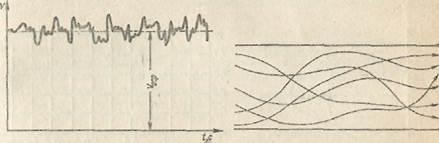
Рнс. 1.54. Пульсация скорости в тур- Рис. 1.55. Характер линий тока в
булентном потоке турбулентном потоке
строго говоря, турбулентное течение всегда является неустановившимся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осредненпые по времени значения скоростей и давлений, а также полный расход потока пе изменяются со временем. Такое течение встречается на практике достаточно часто.
18. Особенности турбулентного движения жидкости. Пульсация скоростей и давлений. Касательное напряжение в турбулентоном потке.
Распределение скоростей при турбулентном течении более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении, для которого характерен параболический закон распределения скоростей.
В связи с этим коэффициент Кориолиса а, учитывающий неравномерность распределения скоростей в уравнении Бернулли, при турбулентном течении значительно меньше, нежели при ламинарном. В отличие от ламинарного течения, где а
не зависит от Rе и равен 2, здесь коэффициент а
является функцией Rе и уменьшается с увеличением последнего от 1,13 при Rе ==Rекр
до 1,025 при Rе = 3-106
. Как видно из графика,
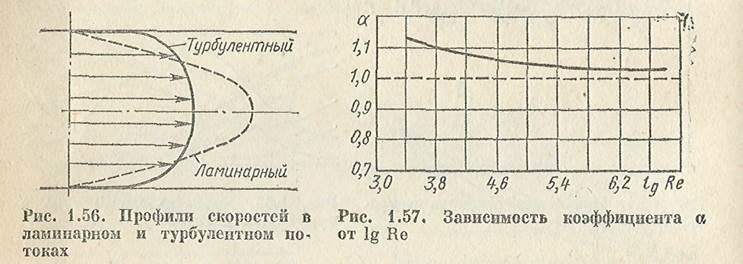
приведенного на рис. 1.57 *, кривая а
при возрастании числа Ке приближается к единице, поэтому в большинстве случаев при турбулентном течении можно принимать а
= 1.
Так как при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае выражает лишь малую часть полного касательного напряжения. Благодаря перемешиванию жидкости и непрерывному переносу количества движения в поперечном направлении касательное напряжение т0
на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном, при тех же значениях числа Rе и динамического давления 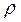 V2
/2, подсчитанных по средней скорости потока. V2
/2, подсчитанных по средней скорости потока.
19. Потери энергии на трение по длинне турбулентного потока в круглом трубопроводе.
Если при ламинарном течении потеря напора на трение возрастает пропорционально скорости (расходу) в первой степени, то при переходе к турбулентному течению заметны некоторый скачок сопротивления и затем более крутое нарастание величины hтр
по кривой, близкой к параболе второй степени.
Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него не имеется достаточно строгой и точной теории. Существуют полуэмпирические, приближенные теории, например теория Праидтля ** и другие, которые здесь не рассматриваются.
* Впервые получен Б. Б. Некрасовым
В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе теории гидродинамического подобия.
Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является уже приводившаяся выше как эмпирическая формула , называемая формулой Вейсбаха— Дарси и имеющая следующий вид
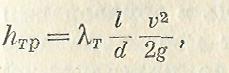
Эта основная формула применима как при турбулентном, так и при ламинарном течении, различие заключается лишь в значениях коэффициента  ,.
Так как при турбулентном течении потеря напора на трение приблизительно пропорциональна скорости (и расходу) во второй степени, коэффициент потерь на трение в формуле в первом приближении для данной трубы можно считать величиной постоянной. ,.
Так как при турбулентном течении потеря напора на трение приблизительно пропорциональна скорости (и расходу) во второй степени, коэффициент потерь на трение в формуле в первом приближении для данной трубы можно считать величиной постоянной.
20. Коэффициент гпдоавлического трения в турбулентном потоке. Понятие шероховатости иее влияние на
 . .
Однако из закона гидродинамического подобия следует, что коэффициент  так же, как и так же, как и л
,
должен быть функцией основного критерия подобия напорных потоков — числа Рейнольдса Rе, а также может зависеть от безразмерного геометрического фактора — относительной шероховатости внутренней поверхности трубы, т. е. л
,
должен быть функцией основного критерия подобия напорных потоков — числа Рейнольдса Rе, а также может зависеть от безразмерного геометрического фактора — относительной шероховатости внутренней поверхности трубы, т. е.  =f(Rе, =f(Rе, 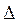 /d), где /d), где 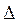 — средняя высота бугорков шероховатости, d,
— диаметр трубы. — средняя высота бугорков шероховатости, d,
— диаметр трубы.
Когда шероховатость трубы не влияет на ее сопротивление (на  т
), трубу называют гидравлически гладкой. Для этих случаев коэффициент Rт
является функцией лишь числа Рейнольдса: т
), трубу называют гидравлически гладкой. Для этих случаев коэффициент Rт
является функцией лишь числа Рейнольдса:  т
=
f
1
(Rе). Существует ряд эмпирических и полуэмпирических формул, выражающих эту функцию для турбулентного течения в гидравлически гладких трубах; одной из наиболее удобных и употребительных является формула П. К. Конакова т
=
f
1
(Rе). Существует ряд эмпирических и полуэмпирических формул, выражающих эту функцию для турбулентного течения в гидравлически гладких трубах; одной из наиболее удобных и употребительных является формула П. К. Конакова 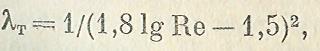
применимая при числе Rе от Rекр
до Rе, равного нескольким миллионам.
При 2300 < Ке < 108
можно пользоваться также формулой Блазиуса
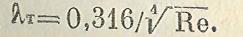
21. Графики Нмкурадзе
И. И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределенная зернистая шероховатость.
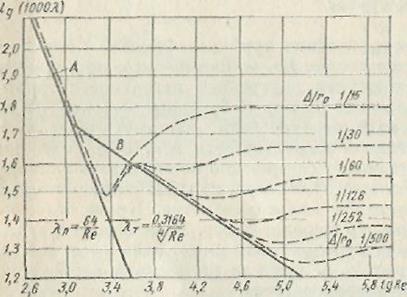 Первая область — область малых Rе и Первая область — область малых Rе и 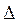 /г0
, где коэффициент /г0
, где коэффициент т
от шероховатости не зависит, а определяется лишь числом Rе; это область гидравлически гладких труб. Она не имеет места для максимальных значений шероховатости в опытах И. И. Никурадзе. т
от шероховатости не зависит, а определяется лишь числом Rе; это область гидравлически гладких труб. Она не имеет места для максимальных значений шероховатости в опытах И. И. Никурадзе.
Во второй области коэффициент  т
зависит одновременно от двух параметров — числа Rе и относительной шероховатости. т
зависит одновременно от двух параметров — числа Rе и относительной шероховатости.
Третья область — область больших Rе и 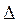 /г0
, где коэффициент /г0
, где коэффициент т
не зависит от Rе, а определяется лишь относительной шероховатостью. Эту область называют областью автомоделыюсти или режимом квадратичного сопротивления, так как независимость коэффициента т
не зависит от Rе, а определяется лишь относительной шероховатостью. Эту область называют областью автомоделыюсти или режимом квадратичного сопротивления, так как независимость коэффициента  т
от Ве означает, что потеря напора пропорциональна скорости во второй степени т
от Ве означает, что потеря напора пропорциональна скорости во второй степени
Чтобы лучше уяснить эти особенности сопротивления шероховатых труб, необходимо учесть наличие ламинарного слоя
Как указывалось выше, при увеличении Ве толщина ламинарного слоя 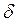 л
уменьшается, поэтому для турбулентного потока при малых Rе толщина ламинарного слоя больше высоты бугорков шероховатости, последние находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. По мере увеличения Rе толщина л
уменьшается, поэтому для турбулентного потока при малых Rе толщина ламинарного слоя больше высоты бугорков шероховатости, последние находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. По мере увеличения Rе толщина 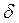 л
уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на сопротивление. При больших Rе толщина ламинарного слоя становится весьма малой, а бугорки шероховатости обтекаются турбулентным потоком с вихре-образованиями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, характерный для данной области. л
уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на сопротивление. При больших Rе толщина ламинарного слоя становится весьма малой, а бугорки шероховатости обтекаются турбулентным потоком с вихре-образованиями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, характерный для данной области.
График И. И. Никурадзе позволяет построить примерную зависимость от Ве допустимой шероховатости, т. е. такого максимального значения, при котором шероховатость трубы еще не влияет на ее сопротивление. Для этого следует взять те точки на графике (см. рис.), в которых кривые для шероховатых труб начинают отклоняться от прямой В
для гладких труб. Очевидно, что с увеличением Rе значение допустимой шероховатости уменьшается.
22. Основные виды местных сопротивлений. Коэф местных потерь
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местных сопротивлений представляют собой соединения или комбинации перечисленных простейших сопротивлений. Так, например, при течении жидкости через вентиль поток искривляется, меняет свое направление, сужается и, наконец, расширяется до первоначальных размеров; при этом возникают интенсивные вихреобразованйя.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе. Коэффициенты потерь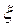 ,
при турбулентном течении определяются в основном формой местных сопротивлений и очень мало изменяются с изменением абсолютных размеров русла, скорости потока и вязкости ,
при турбулентном течении определяются в основном формой местных сопротивлений и очень мало изменяются с изменением абсолютных размеров русла, скорости потока и вязкости 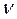 жидкости, т. е. с изменением числа Re, поэтому обычно принимают, что они не зависят от Rе, что означает квадратичный закон сопротивления, или автомодельность. жидкости, т. е. с изменением числа Re, поэтому обычно принимают, что они не зависят от Rе, что означает квадратичный закон сопротивления, или автомодельность.
24. Диффузор (постепенное расширение потока). Потери энергии при плавном расширению
Постепенно расширяющаяся труба называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. Частицы движущейся жидкости преодолевают нарастающее давление за счет своей кинетической энергии, которая уменьшается вдоль диффузора и, что особенно важно, в направлении от оси к стенке. Слои жидкости, прилежащие к стенкам, обладают столь малой кинетической энергией, что иногда оказываются не в состоянии преодолевать повышенное давление, они останавливаются или даже начинают двигаться обратно. Обратное движение (противоток) вызывает отрыв основного потока от стенки и вихреобразования (рис. 1.64). Интенсивность этих явлений возрастает с увеличением угла расширения диффузора, а вместе с этим растут и потери на вихреобразования в нем.
Полную потерю напора hдиф
в диффузоре условно рассматриваем как сумму двух слагаемых: hдиф = hтр
+ hрасш
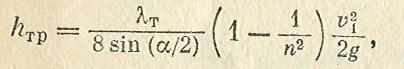
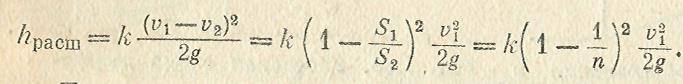
26. Конфузор (постепенное сужение потока) Потери энергии потока в нем
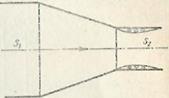 Постепенное сужение трубы, т. е. коническая сходящаяся труба, называется конфузором . Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления; так как давление жидкости в начале конфузора выше, чем в конце, причин к возникновению вихреобразований и срывов потока (как в диффузоре) нет. В конфузоре имеются лишь потери на трение. В связи с этим сопротивление конфузора всегда меньше, чем сопротивление такого же диффузора. Постепенное сужение трубы, т. е. коническая сходящаяся труба, называется конфузором . Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления; так как давление жидкости в начале конфузора выше, чем в конце, причин к возникновению вихреобразований и срывов потока (как в диффузоре) нет. В конфузоре имеются лишь потери на трение. В связи с этим сопротивление конфузора всегда меньше, чем сопротивление такого же диффузора.
Потерю напора на трение в конфузоре можно подсчитать так же, как это делали для диффузора, т. е. сначала выразить потерю для элементарного отрезка, а затем выполнить интегрирование. В результате получим следующую формулу: 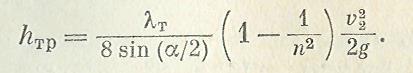
Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Для ликвидации вихреобразований и связанных с ним потерь рекомендуется коническую часть плавно сопрягать с цилиндрической или коническую часть заменять криволинейной, плавно переходящей в цилиндрическую. При этом можно допустить значительную степень сужения п
при небольшой длине вдоль оси и небольших потерях.
Коэффициент сопротивления такого плавного сужения, называемого соплом, изменяется примерно в пределах 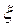 =0,03-0,1 в зависимости от степени и плавности сужения и Rе (большим Rе соответствуют малые значения =0,03-0,1 в зависимости от степени и плавности сужения и Rе (большим Rе соответствуют малые значения 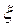 и наоборот) и наоборот)
27. Истечение жидкостей через малое отверстие в тонкой стенке с острой кромкой
Пусть отверстие имеет форму, показанную на рис. 1.79, а,
т. е. выполнено в виде сверления в тонкой стенке без обработки входной Л
кромки или имеет форму, показанную на рис. 1.79, б,
т. е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Условия истечения жидкости в этих двух случаях будут совершенно одинаковыми: частицы жидкости приближаются к отверстию из всего прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см. рис. 1.79, а).
Струя отрывается от стенки у кромки отверстия и затем несколько сжимается. Цилин-100
|