|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
Государственное образовательное учреждение высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет: Теплоэнергетический
Кафедра: Автоматизации теплоэнергетических процессов
Специальность: 220301 «Автоматизация технологических процессов и производств (в теплоэнергетике)»
Курсовая работа по ТАУ
Расчёт одноконтурной системы автоматического регулирования
Вариант №7
Исполнитель
студент гр.6241: Коростелев А.А.
Руководитель
преподаватель: Татарников А.А.
Томск 2007
Аннотация
В данной курсовой работе представлены расчёт и построение границы заданного запаса устойчивости, одноконтурной АСР с ПИ-регулятором, корневым методом с использованием РАФЧХ. Рассмотрен процесс определения оптимальных параметров настройки регулятора, произведены расчёт и построение переходных процессов в замкнутой АСР при возмущении f, идущем по каналу регулирующего воздействия, и при сигнале задания S. После каждого из графиков данных переходных процессов произведена оценка качества этих процессов.
Содержание
Введение……………………………………………………………………………………….……….4
1. Расчёт оптимальных параметров настройки(ОПН) ………………………………………….…..5
1.1 Расчёт и построение границы заданного запаса устойчивости АСР …………………..……...5
1.2 Обоснование и выбор ОПН регулятора……………………………….…………………….….10
2. Расчёт, построение и оценка качества переходного процесса по каналу S -Y ……………..…11
3. Расчёт, построение и оценка качества переходного процесса по каналу f -Y ……………...…15
Заключение…………………………………………………………………………………………....20
Введение
Данная курсовая работа посвящена расчёту одноконтурной системы автоматического регулирования. Для оценки систем регулирования с точки зрения их практической пригодности необходимо определить, в каких условиях эти системы можно использовать, какие настроечные параметры регулятора требуется установить, чтобы процесс регулирования, осуществляемый при помощи различных регуляторов систем, был оптимальным.
В настоящее время системы регулирования получили широкое применение в различных отраслях промышленности. В связи с этим проблема определения оптимальных параметров настройки регуляторов систем остаётся актуальной, даже несмотря на то, что разработано большое количество приёмов и методов, позволяющих решать эти проблемы. В частности, существует два инженерных метода расчёта систем регулирования: корневой (с использованием РАФЧХ) и частотный по максимуму АЧХ замкнутой системы (метод В.Я. Ротача).
В данной курсовой работе приводятся расчёта заданной АСР, исходные данные и структурная схема которой представлены в задании на выполнение курсовой работы. Первый пункт посвящен расчёту и построению границы заданного запаса устойчивости АСР с ПИ-регулятором и объектом регулирования, корневым методом. А также обоснование и выбор оптимальных параметров настройки. Второй пункт посвящён расчёту переходного процесса по каналу регулирующего воздействия S-Y, и прямой оценки качества этого процесса. Третий пункт содержит расчёт переходного процесса при возмущении f, идущему по каналу воздействия. А также произведены оценки прямых критериев качества.
1. Расчёт оптимальных параметров настройки (ОПН).
1.1 Расчёт и построение границы заданного запаса устойчивости АСР.
Для расчёта и построения границы заданного запаса устойчивости АСР с ПИ-регулятором, представленной на рисунке 1, воспользуемся корневым методом параметрического синтеза систем автоматического регулирования с применением расширенных амплитудно-фазовых частотных характеристик (РАФЧХ).
Используя исходные данные, приведенные в таблице 1, можем записать, что для заданной системы регулирования установлены следующие требования к запасу устойчивости системы: степень затухания переходного процесса в системе . .
Исходя из этого можно определить, зависимость между степенью затухания переходных процессов в заданной системе регулирования ψ и степенью колебательности переходных процессов в заданной системе регулирования m, по таблице соответствия оценок запаса устойчивости приведённой ниже.
| 
|
0
|
0.75
|
0.80
|
0.265
|
0.90
|
0.95
|
0.998
|
1.0
|
| m
|
0
|
0.221
|
0.265
|
0.305
|
0.366
|
0.478
|
1.0
|
∞
|
Эта таблица была получена на основе следующего соотношения:
 (1) (1)
где ψ - степенью затухания;
m – степень колебательности;
Передаточная функция объекта регулирования согласно исходных данных определяется по формуле:
 (2) (2)
где Р – оператор Лапласа;
К – коэффициент передачи;
При n=2 выражение для  примет вид: примет вид:
 (3) (3)
Используя данные таблицы 1 подставляем значения параметров в выражение (3). После подстановки значений параметров получаем окончательное выражение для передаточной функции объекта регулирования:
 (4) (4)
Определим расширенные частотные характеристики объекта регулирования. Расширенные частотные характеристики какого-либо звена можно получить подстановкой в передаточную функцию этого звена W(P), оператора  или или  , в выражениях для оператора Лапласа ω – частота, с-1
. В первом случае расчётные формулы метода обеспечивают получение границы заданной степени колебательности системы m, а во втором - получение границы заданной степени устойчивости системы , в выражениях для оператора Лапласа ω – частота, с-1
. В первом случае расчётные формулы метода обеспечивают получение границы заданной степени колебательности системы m, а во втором - получение границы заданной степени устойчивости системы  в пространстве параметров настройки регулятора. в пространстве параметров настройки регулятора.
Так как заданно значение колебательности, заменяем в формуле (4) оператор  , в результате получаем выражение для РАФЧХ объекта регулирования: , в результате получаем выражение для РАФЧХ объекта регулирования:
 (5) (5)
Используя математический пакет MAthCad, предварительно задав начальное значение частоты  =0 с-1
и шаг по частоте =0 с-1
и шаг по частоте  с-1
, рассчитываем расширенные частотные характеристики объекта при изменении частоты до ω=0,20 с-1
. с-1
, рассчитываем расширенные частотные характеристики объекта при изменении частоты до ω=0,20 с-1
.
Расширенная вещественная частотная характеристика (РВЧХ):
Reоб
(m,ω)=Re(Wоб
(m,iω)) (6)
Расширенная мнимая частотная характеристика (РМЧХ):
Imоб
(m,ω)=Im(Wоб
(m,iω)) (7)
Расширенная амплитудно-частотная характеристика (РАЧХ)
 (8) (8)
Расширенная фазо-частотная характеристика (РФЧХ):
 (9) (9)
Результаты расчётов сведём в таблицу 2, приведенную ниже.
Таблица 2 – Расширенные частотные характеристики объекта регулирования
| частота ω, с-1
|
Reоб
(m,ω)
|
Imоб
(m,ω)
|
Аоб
(m,ω)
|
φоб
(m,ω), рад
|
| 0,001
|
1.548
|
-0.178
|
1.558
|
-0.114
|
| 0,003
|
1.562
|
-0.47
|
1.631
|
-0.292
|
| 0,004
|
1.493
|
-0.772
|
1.681
|
-0.477
|
| 0,006
|
1.341
|
-1.049
|
1.702
|
-0.664
|
| 0,007
|
1.118
|
-1.273
|
1.695
|
-0.85
|
| 0,008
|
0.852
|
-1.425
|
1.648
|
-1.032
|
| 0.01
|
0.571
|
-1.499
|
1.604
|
-1.207
|
| 0.011
|
0.301
|
-1.501
|
1.531
|
-1.373
|
Окончание таблицы 2
| частота ω, с-1
|
Reоб
(m,ω)
|
Imоб
(m,ω)
|
Аоб
(m,ω)
|
φоб
(m,ω), рад
|
| 0.013
|
0.06
|
-1.446
|
1.448
|
-1.529
|
| 0.014
|
-0.142
|
-1.352
|
1.359
|
-1.675
|
| 0.016
|
-0.303
|
-1.233
|
1.269
|
-1.812
|
| 0.017
|
-0.425
|
-1.102
|
1.181
|
-1.938
|
| 0.019
|
-0.512
|
-0.97
|
1.097
|
-2.057
|
| 0.021
|
-0.57
|
-0.841
|
1.017
|
-2.166
|
| 0.022
|
-0.605
|
-0.721
|
0.942
|
-2.269
|
| 0.024
|
-0.622
|
-0.612
|
0.872
|
-2.364
|
| 0.025
|
-0.624
|
-0.513
|
0.808
|
-2.454
|
| 0.027
|
-0.616
|
-0.426
|
0.749
|
-2.537
|
| 0.028
|
-0.601
|
-0.349
|
0.695
|
-2.615
|
| 0.03
|
-0.58
|
-0.283
|
0.645
|
-2.688
|
| 0.031
|
-0.556
|
-0.225
|
0.6
|
-2.757
|
| 0.033
|
-0.531
|
-0.176
|
0.559
|
-2.822
|
| 0.034
|
-0.504
|
-0.134
|
0.521
|
-2.883
|
| 0.036
|
-0.477
|
-0.097
|
0.487
|
-2.94
|
| 0.037
|
-0.451
|
-0.067
|
0.455
|
-2.995
|
| 0.039
|
-0.425
|
-0.041
|
0.427
|
-3.046
|
| 0.04
|
-0.4
|
-0.019
|
0.4
|
-3.095
|
| 0.042
|
-0.376
|
1.212e-4
|
0.376
|
3.141
|
Расчётные формулы корневого метода для ПИ- регулятора имеют следующий вид:
 (10) (10)
 (11) (11)
В вышеприведенных формулах (10) и (11)  - коэффициент передачи ПИ- регулятора, - коэффициент передачи ПИ- регулятора,  - постоянная интегрирования ПИ- регулятора или время изодрома. - постоянная интегрирования ПИ- регулятора или время изодрома.
Зададим диапазон изменения частоты  с-1
с шагом с-1
с шагом  c-1
, определим настройки регулятора c-1
, определим настройки регулятора  и Кр
в заданном диапазоне частот. Результаты расчётов сведём в таблицу 3. и Кр
в заданном диапазоне частот. Результаты расчётов сведём в таблицу 3.
частота ω, с-1
Таблица 3 –Результаты расчёта настройки ПИ- регулятора в заданном диапазоне частот
| w
|
Kp
|
Kp/Tu
|
| 0,0010
|
-0.611
|
0,0001
|
| 2.5e-3
|
-0.522
|
0,0005
|
| 0,0040
|
-0.429
|
0,0013
|
| 5.5e-3
|
-0.33
|
0,0024
|
| 0,0070
|
-0.227
|
0,0035
|
| 8.5e-3
|
-0.12
|
0,0049
|
| 0.01
|
-8.723e-3
|
0,0066
|
| 0.011
|
0.106
|
0,0084
|
| 0.013
|
0.224
|
0.01
|
| 0.014
|
0.345
|
0.012
|
| 0.016
|
0.468
|
0.014
|
| 0.017
|
0.593
|
0.016
|
Окончание таблицы 3
| частота ω, с-1
|
Kp
|
Kp/Tu
|
| 0.019
|
0.721
|
0.017
|
| 0.021
|
0.85
|
0.019
|
| 0.022
|
0.98
|
0.02
|
| 0.024
|
1.112
|
0.021
|
| 0.025
|
1.244
|
0.022
|
| 0.027
|
1.376
|
0.023
|
| 0.028
|
1.509
|
0.023
|
| 0.03
|
1.641
|
0.023
|
| 0.031
|
1.773
|
0.022
|
| 0.033
|
1.904
|
0.021
|
| 0.034
|
2.034
|
0.019
|
| 0.036
|
2.163
|
0.017
|
| 0.037
|
2.301
|
0.013
|
| 0.039
|
2.415
|
9.737e-3
|
| 0.04
|
2.537
|
5.243e-3
|
| 0.042
|
2.658
|
-4.031e-5
|
По данным таблицы 3 построим график зависимости  =f(Kp
) ,т.е укажем границу заданного запаса устойчивости системы регулирования на рисунке 3. =f(Kp
) ,т.е укажем границу заданного запаса устойчивости системы регулирования на рисунке 3.
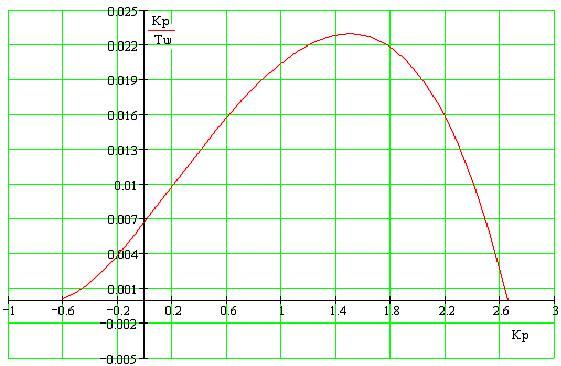
Рисунок 3 - Область параметров настройки ПИ- регулятора
Полученная кривая является линией заданной степени затухания Ψ= Ψзад
=0,9 процесса регулирования, что соответствует степени колебательности m=0.366. Таким образом, все значения  и Kp
, лежащие на этой кривой, обеспечивают определенную степень затухания (в данном случае Ψ= Ψзад
=0,9). и Kp
, лежащие на этой кривой, обеспечивают определенную степень затухания (в данном случае Ψ= Ψзад
=0,9).
Значения  и Kp
, лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат процесс регулирования со степенью затухания больше заданного (Ψ1
> Ψзад
), а лежащие вне этой области – со степенью затухания меньше заданной (Ψ1
<Ψзад
). и Kp
, лежащие внутри области, ограниченной данной кривой и осями координат, обеспечат процесс регулирования со степенью затухания больше заданного (Ψ1
> Ψзад
), а лежащие вне этой области – со степенью затухания меньше заданной (Ψ1
<Ψзад
).
3.2 Обоснование и выбор ОПН регулятора.
Поиск оптимальных параметров настройки регулятора осуществляется вдоль границы заданного запаса устойчивости системы регулирования, представленной на рисунке 3, до достижения экстремума заданного критерия качества. В задании на курсовую работу в качестве принятого критерия качества указан второй интегральный критерий.
Минимуму первого интегрального критерия  на графике (рисунок 3) соответствует точка, в которой на графике (рисунок 3) соответствует точка, в которой  принимает значение равное 0,95 от максимального в сторону увеличения частоты. Эта точка и определит оптимальные параметры настройки ПИ- регулятора. Используя данные таблицы 3 и рисунка 3, находим, что точке максимума соответствуют значения: принимает значение равное 0,95 от максимального в сторону увеличения частоты. Эта точка и определит оптимальные параметры настройки ПИ- регулятора. Используя данные таблицы 3 и рисунка 3, находим, что точке максимума соответствуют значения:
 , Kp
= 1.509 при ω = 0.028 с-1
. , Kp
= 1.509 при ω = 0.028 с-1
.
Поэтому оптимальные параметры настройки ПИ- регулятора имеют значения:
 , Kp
∙ 0,95= 1.433 , , Kp
∙ 0,95= 1.433 ,  с. с.
2. Расчёт, построение, и оценка качества переходного процесса по каналу регулирующего воздействия
S
-
Y
Для одноконтурной системы регулирования, приведенной на рисунке 1, определим передаточную функцию замкнутой АСР по каналу S-Y из соотношения:
 (12) (12)
где передаточная функция объекта регулирования  , ,
передаточная функция ПИ- регулятора  . .
После подстановки значения  в формулу (12), получаем окончательное выражение для передаточной функции замкнутой АСР по каналу S-Y: в формулу (12), получаем окончательное выражение для передаточной функции замкнутой АСР по каналу S-Y:
 (13) (13)
Получим выражение для АФЧХ замкнутой системы путём замены оператора p в формуле (13) на  , в результате получаем: , в результате получаем:
 (14) (14)
Используя математический пакет MathCad, предварительно задав диапазон изменения частоты  с-1
с шагом с-1
с шагом  c-1
, рассчитываем вещественную частотную характеристику замкнутой АСР при регулирующем воздействии: ReЗ.С..1
(ω). Результаты расчёта сведём в таблицу 4. c-1
, рассчитываем вещественную частотную характеристику замкнутой АСР при регулирующем воздействии: ReЗ.С..1
(ω). Результаты расчёта сведём в таблицу 4.
Таблица 4 – Результаты расчёта ВЧХ замкнутой АСР при регулирующем воздействии
| частота ω, с-1
|
Reоб
(m,ω)
|
| 0,001
|
1.001
|
| 0,009
|
1.041
|
| 0.017
|
1.043
|
| 0.025
|
0.369
|
| 0.033
|
-0.674
|
| 0.041
|
-0.641
|
| 0.049
|
-0.452
|
| 0.057
|
-0.32
|
Продолжение таблицы 4
| частота ω, с-1
|
Reоб
(m,ω)
|
| 0.065
|
-0.235
|
| 0.073
|
-0.178
|
| 0.081
|
-0.138
|
| 0.089
|
-0.109
|
| 0.097
|
-0.088
|
| 0.105
|
-0.071
|
| 0.113
|
-0.058
|
| 0.121
|
-0.048
|
| 0.129
|
-0.04
|
| 0.137
|
-0.033
|
| 0.145
|
-0.027
|
| 0.153
|
-0.023
|
| 0.161
|
-0.019
|
| 0.169
|
-0.015
|
| 0.177
|
-0.012
|
| 0.185
|
-0,0098
|
| 0.193
|
-0,0078
|
По данным таблицы 4 строим график ВЧХ замкнутой АСР, который приведен на рисунке 4.

 Рисунок 4 - График ВЧХ замкнутой АСР при регулирующем воздействии Рисунок 4 - График ВЧХ замкнутой АСР при регулирующем воздействии
Переходный процесс в замкнутой АСР по каналу S-Y можно рассчитать по методу трапеций, используя график ВЧХ замкнутой АСР, приведенный на рисунке 4.
Установлено, что переходная характеристика какой- либо системы y(t) связана с ВЧХ этой системы Re(ω) выражением:
 (15) (15)
где t – время переходного процесса в замкнутой АСР.
Для более точного расчёта в качестве верхнего предела интеграла для y(t) принимают не  , а значение частоты, при которой график Re(ω) стремится к 0, т.е частоту среза ωСР
. По графику, приведенному на рисунке 4, определяем, ωСР
=0,2 с-1
. Поэтому переходный процесс в замкнутой АСР по каналу S-Y можно рассчитать по формуле: , а значение частоты, при которой график Re(ω) стремится к 0, т.е частоту среза ωСР
. По графику, приведенному на рисунке 4, определяем, ωСР
=0,2 с-1
. Поэтому переходный процесс в замкнутой АСР по каналу S-Y можно рассчитать по формуле:
 (16) (16)
Задав диапазон изменения времени переходного процесса  с и шаг с и шаг  с, рассчитываем переходный процесс в замкнутой АСР по каналу S-Y. Результаты расчета сведём в таблицу 5. с, рассчитываем переходный процесс в замкнутой АСР по каналу S-Y. Результаты расчета сведём в таблицу 5.
Таблица 5 – Результаты расчёта переходного процесса в замкнутой АСР по каналу S-Y
| t, c
|
Ys-y(t)
|
| 0
|
0,000
|
| 30
|
0.189
|
| 60
|
0.722
|
| 90
|
1.169
|
| 120
|
1,330
|
| 150
|
1.245
|
| 180
|
1,070
|
| 210
|
0.937
|
| 240
|
0.898
|
| 270
|
0.931
|
| 300
|
0.986
|
| 330
|
1.024
|
| 360
|
1.032
|
| 390
|
1,020
|
| 420
|
1.002
|
| 450
|
0.992
|
| 480
|
0.99
|
| 510
|
0.994
|
| 540
|
1,000
|
| 570
|
1.003
|
| 600
|
1.003
|
| 630
|
1.001
|
| 660
|
1,000
|
| 690
|
0.999
|
По данным таблицы 5 строим график переходного процесса в замкнутой АСР по
каналу S-Y, который приведён на рисунке 5.
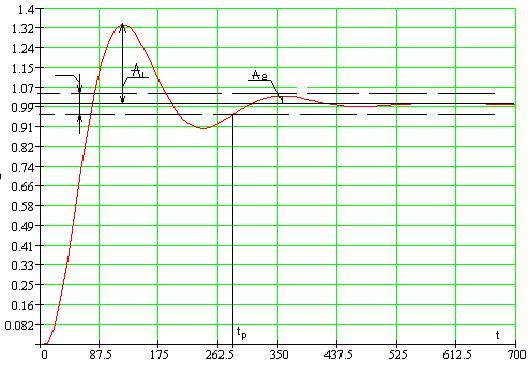  
Рисунок 5 - График переходного процесса в замкнутой АСР по каналу S-Y
Используя данные таблицы 5 и рисунка 5, произведём оценку качества переходного процесса в замкнутой АСР по каналу S-Y.
Прямые критерии качества:
1.Максимальная динамическая ошибка: А1
=0,34;
2.Перерегулирование:  (17) (17)
где  - уровень установившегося значения регулируемой величины при времени переходного процесса - уровень установившегося значения регулируемой величины при времени переходного процесса  , равного , равного  ; ;
3.Динамический коэффициент регулирования Rд не определяется для такого типа процессов;
4.Степень затухания переходного процесса:  (18) (18)
где  - второй максимальный выброс регулируемой величины; - второй максимальный выброс регулируемой величины;
5.Статическая ошибка:  (19) (19)
где S – сигнал регулирующего воздействия 1(t);
6.Время регулирования:  при величине при величине  , значение которой задают для контроля переходного процесса с заданной степенью точности. , значение которой задают для контроля переходного процесса с заданной степенью точности.
Все приведенные выше критерии качества указаны на рисунке 5.
3. Расчёт, построение и оценка качества переходного процесса по каналу
f
-
Y
Для одноконтурной системы регулирования, приведенной на рисунке 1, определим передаточную функцию замкнутой АСР по каналу f -Y по формуле:
 (20) (20)
После подстановки выражения для  в формулу (7), получаем окончательное выражение для передаточной функции замкнутой АСР по каналу f -Y: в формулу (7), получаем окончательное выражение для передаточной функции замкнутой АСР по каналу f -Y:
 (21) (21)
Получим выражение для АФЧХ замкнутой системы путём замены оператора p в формуле (18) на  , в результате получаем: , в результате получаем:
 (22) (22)
Используя математический пакет MAthCad, предварительно задав диапазон изменения частоты  с-1
с шагом с-1
с шагом  c-
, рассчитываем вещественную частотную характеристику замкнутой АСР: ReЗ.С.2
(ω). Результаты расчёта сведём в таблицу 6. c-
, рассчитываем вещественную частотную характеристику замкнутой АСР: ReЗ.С.2
(ω). Результаты расчёта сведём в таблицу 6.
Таблица 6 - Результаты расчёта ВЧХ замкнутой АСР при возмущении f
| частота ω, с-1
|
Reоб
(m,ω)
|
| 0.01
|
0.315
|
| 0.02
|
0.772
|
| 0.03
|
0.158
|
| 0.04
|
-0.306
|
| 0.05
|
-0.256
|
| 0.06
|
-0.185
|
| 0.07
|
-0.135
|
| 0.08
|
-0.101
|
| 0.09
|
-0.077
|
| 0.1
|
-0.06
|
| 0.11
|
-0.047
|
| 0.12
|
-0.037
|
| 0.13
|
-0.03
|
| 0.14
|
-0.024
|
| 0.15
|
-0.019
|
| 0.16
|
-0.015
|
| 0.17
|
-0.012
|
| 0.18
|
-0,0093
|
| 0.19
|
-0,0071
|
| 0.2
|
-0,054
|
По данным таблицы 6 строим график ВЧХ замкнутой АСР при возмущении f, который приведен на рисунке 6
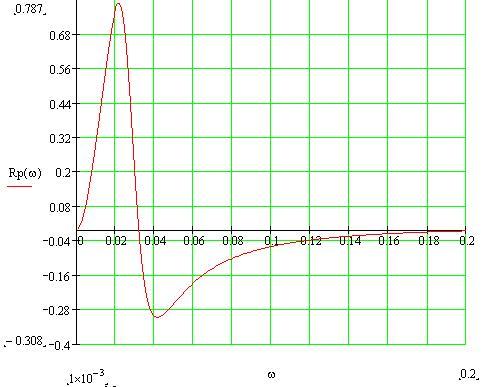
Рисунок 6 – График ВЧХ замкнутой АСР при возмущении f
Переходный процесс в замкнутой АСР по каналу f-Y можно рассчитать по методу трапеций, используя график ВЧХ замкнутой АСР при возмущении f (рисунок 6).
Поэтому переходный процесс в замкнутой АСР по каналу F-Y можно рассчитать по формуле:
 (23) (23)
Как уже было сказано выше, для более точного расчёта в качестве верхнего предела интеграла для YF
-
Y
(t) принимают значение частоты среза ωСР.
По графику, приведенному на рисунке 6, определяем, что ωСР
=0,2 с-1
.
Задав диапазон изменения времени переходного процесса  с и шаг с и шаг  с, рассчитываем переходный процесс в замкнутой АСР по каналу f-Y. Результаты расчета сведём в таблицу 7, приведенную ниже. с, рассчитываем переходный процесс в замкнутой АСР по каналу f-Y. Результаты расчета сведём в таблицу 7, приведенную ниже.
Таблица 7 - Результаты расчёта переходного процесса в замкнутой АСР по каналу f-Y
| t, c
|
Ys-y(t)
|
| 0
|
0
|
| 30
|
0.116
|
| 60
|
0.37
|
| 90
|
0.472
|
| 120
|
0.374
|
| 150
|
0.181
|
| 180
|
0.014
|
| 210
|
-0.063
|
| 240
|
-0.059
|
| 270
|
-0.017
|
| 300
|
0.02
|
| 330
|
0.033
|
| 360
|
0.024
|
| 390
|
0,0034
|
| 420
|
-0,0047
|
| 450
|
-0,0087
|
| 480
|
-0,0067
|
| 510
|
-0,013
|
| 540
|
0,021
|
| 570
|
0,034
|
| 600
|
0,018
|
| 630
|
0,0024
|
| 60
|
-0,0065
|
| 690
|
-0,0093
|
По данным таблицы 7 строим график переходного процесса в замкнутой АСР по каналу f-Y, представленный на рисунке 7.

Рисунок 7 - График переходного процесса в замкнутой АСР по каналу f-Y
Используя данные таблицы 7 и рисунка 7, произведём оценку качества переходного процесса в замкнутой АСР по каналу F-Y.
Прямые критерии качества:
1.Максимальная динамическая ошибка: А1=0,47;
2.Перерегулирование:  (24) (24)
где  - первое минимальное отклонение регулируемой величины; - первое минимальное отклонение регулируемой величины;
3.Динамический коэффициент регулирования RД
:  (25) (25)
где  - коэффициент передачи объекта; - коэффициент передачи объекта;
4.Степень затухания переходного процесса:  ; (26) ; (26)
5.Статическая ошибка:  ; ;
6.Время регулирования:  при величине при величине  . .
Так как в заданной АСР, представленной на рисунке 2, имеется звено чистого транспортного запаздывания с передаточной функцией  , то переходные процессы в этой системе имеет запаздывание на величину 4 с относительно их начала. Для наглядности указанного факта изобразим начальные части графиков переходных процессов по каналам S-Y и f-Y соответственно на рисунке 8 и 9. , то переходные процессы в этой системе имеет запаздывание на величину 4 с относительно их начала. Для наглядности указанного факта изобразим начальные части графиков переходных процессов по каналам S-Y и f-Y соответственно на рисунке 8 и 9.

Рисунок 8 – Начальный участок графика переходного процесса в замкнутой АСР по каналу S-Y
 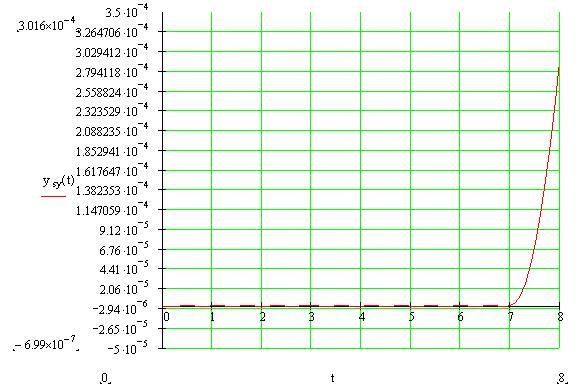
Рисунок 9 – Начальный участок графика переходного процесса в замкнутой АСР по каналу f-Y
Заключение
Определение оптимальных параметров настройки регуляторов, расчёт различных систем автоматического регулирования, без сомнения, являются одной из главных задач любого инженера. Использование современных систем регулирования требует знания различных методов и приёмов расчёта этих систем, определения и установки требуемых параметров настройки регулятора, основных недостатков и преимуществ разного рода регуляторов по сравнению друг с другом.
В процессе написания курсовой работы был изучен один из двух инженерных методов расчёта одноконтурных систем регулирования: корневой метод (с использованием РАФЧХ). Было выяснено, что оптимальными параметрами настройки какого-либо регулятора считают те параметры, при которых обеспечивается близкий к оптимальному процесс регулирования. Под оптимальным процессом регулирования обычно понимают процесс, удовлетворяющий требованиям к запасу устойчивости системы. Поиск оптимальных параметров настройки осуществляется вдоль границы заданного запаса устойчивости системы регулирования до достижения экстремума принятого критерия качества. В данной курсовой работе, согласно заданию, был принят второй интегральный критерий.
В результате проделанной работы, были получены переходные процессы по каналам S-Y и f-Y. Оценка качества этих процессов показала, что они удовлетворяют требованиям к запасу устойчивости системы, приведенных в исходных данных.
Можно заметить, что переходный процесс по каналу f-Y имеет прямые критерии качества лучше, чем переходный процесс по каналу S-Y:
Таблица 8 – Прямые критерии качества переходных процессов по каналам S-Y и f-Y
| |
S-Y
|
f-Y
|
| Максимальная динамическая ошибка 
|
0,34
|
0.47
|
| Перерегулирование  (%) (%)
|
34
|
14
|
| Степень затухания переходного процесса 
|
0,88
|
0,91
|
| Время регулирования tp
, с
|
270
|
175
|
| Статическая ошибка для этих процессов 
|
0
|
0
|
Следовательно регулятор установленный в канале обратной связи способствует лучшей работе системы нежели он будет установлен в основном канале.
|