| ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Филиал в г. Брянске
Контрольная РАБОТА
по дисциплине
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И ПРИКЛАДНЫЕ МОДЕЛИ
Вариант №2
Брянск – 2009
ЗАДАЧА 1
Задача о раскрое
1.
В обработку поступили две партии досок для изготовления комплектов из трех деталей (треугольные каркасы настилов на стройплощадку), причем первая партия содержит 52 доски длиной по 6,5 м каждая, вторая содержит 200 досок длиной по 4 м каждая. Каждый комплект состоит из двух деталей по 2 м каждая и одной детали в 1,25 м.
Ставится задача поиска рационального варианта раскроя поступившего в обработку материала.
Решение:
Безусловно, в этой задаче о раскрое критерий оптимальности – «максимум выпуска (реализации) комплектной продукции». Построим возможные способы раскроя исходного материала, с этой целью составим таблицу:
| Доска 6,5 м
|
Доска 4 м
|
| 2,0 м
|
1,25 м
|
Отходы
|
2,0 м
|
1,25 м
|
Отходы
|
| х11
(у1
)
|
2
|
2
|
0
|
х21
(у5
)
|
2
|
0
|
0
|
| х12
(у2
)
|
1
|
3
|
0,75
|
х22
(у6
)
|
1
|
1
|
0,75
|
| х13
(у3
)
|
0
|
5
|
0,25
|
х23
(у7
)
|
0
|
3
|
0,25
|
| х14
(у4
)
|
3
|
0
|
0,5
|
Введем необходимые обозначения: х
ij
– число досок из i
-й партии (i=1,2), которое следует раскроить j
-м способом.
Рассмотрим соотношения:
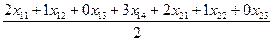
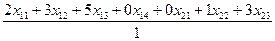 . .
Обозначим через Z-минимальное из этих соотношений (это и будет количество комплектной продукции). Следовательно, экономико-математическая модель примет вид:
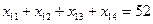 , ,
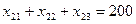 , ,
 , ,
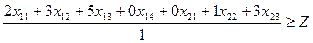 , ,
xij
,
Z
– целые неотрицательные.
Для удобства записи заменим двухиндексные переменные xij
, и Z
на одноиндексные переменные yj
так как это показано в таблице раскроя (Z=
y8
). ЭММ задачи будет иметь вид:
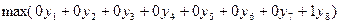
при ограничениях:

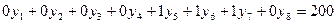

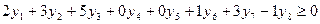
yj
,
j
=1,8 – целые неотрицательные.
В табл.1
приведены указания на ячейки-формулы.
Таблица 1 - Формулы рабочей таблицы
| Ячейка
|
Формула
|
| I7
|
=СУММПРОИЗВ(B4:I4;B5:I5)
|
| J9
|
=СУММПРОИЗВ(B$4:I$4;B9:I9)
|
| J10
|
=СУММПРОИЗВ(B$4:I$4;B10:I10)
|
| J11
|
=СУММПРОИЗВ(B$4:I$4;B11:I11)
|
| J12
|
=СУММПРОИЗВ(B$4:I$4;B12:I12)
|
Реализуя приведенную модель, получим решение:
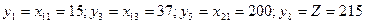
(оптимальные значения остальных переменных равны нулю).
Следовательно, в данной хозяйственной ситуации максимальное количество наборов, равное 215 шт. можно изготовить и реализовать, если:
- раскроить каждую из 15 досок длиной 6,5 м на 2 детали по 2 м и 2 детали по 1,25 м;
- раскроить каждую из 37 досок длиной 6,5 м на 5 деталей по 1,25 м;
- раскроить каждую из 200 досок длиной 4 м на 2 детали по 2 м.
В этом случае мы получим максимальную выручку.
ЗАДАЧА 2
Транспортная задача
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1 тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в матрице планирования.
Требуется:
1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2. Определить, что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами.
Матрица планирования:
| Участок работ
Карьер
|
В1
|
В2
|
В3
|
В4
|
В5
|
Предложение
|
| А
1
|
3
|
3
|
5
|
3
|
1
|
500
|
| А
2
|
4
|
3
|
2
|
4
|
5
|
300
|
| А
3
|
3
|
7
|
5
|
4
|
1
|
100
|
| Потребности
|
150
|
350
|
200
|
100
|
100
|
Решение:
1.
Данная задача является транспортной задачей линейного программирования, закрытой моделью.
1) Создадим форму для решения задачи, т.е. создадим матрицу перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек В3:
F5
вводится «1». Таким образом, резервируется место, где после решения задачи будет находиться распределение перевозок песка на участки ремонта автодорог, обеспечивающее минимальные совокупные транспортные издержки.
2) Введем граничные условия.
Введение условия реализации предложения:
 , ,
где 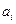 - предложение i
-ого карьера; - предложение i
-ого карьера;
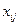 - объем перевозки песка от i
-ого карьера к j
-ому участку работ; - объем перевозки песка от i
-ого карьера к j
-ому участку работ;
n
– количество участков работ.
Для этого просуммируем ячейки B3:
F3
; B4:
F4
; B5:
F5
, поместив результат в ячейки А3
; А4
; А5
соответственно.
Введение условия потребностей участков работ:
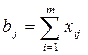 , ,
где b
- потребности j-ого участка работ;
m
- количество карьеров.
Для этого просуммируем ячейки В3:В5
; С3:С5
; D3:
D5
; E3:
E5
; F3:
F5
, поместив результаты в ячейки B6
; C6
; D6
; E6
; F6
соответственно.
3) Введем исходные данные.
В ячейки А11:А13
введем предложение по карьерам, в B10:
F10
потребности по участкам работ, а также удельные затраты по перевозке песка из карьера на участок работ (ячейки B11:
F13
) (см. рис.1
).
Рис. 1 - Ввод исходных данных и граничных условий
4) Назначим целевую функцию.
Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на перевозку, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:
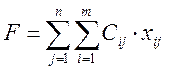 , ,
где 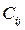 - стоимость доставки 1т песка от i-
ого карьера к j
-ому участку работ; - стоимость доставки 1т песка от i-
ого карьера к j
-ому участку работ;
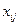 - объем поставки песка от i
-ого карьера к j-
ому участку работ. - объем поставки песка от i
-ого карьера к j-
ому участку работ.
Для этого в ячейку В15
вставим функцию: СУММ ПРОИЗВ (B11:F13;B3:F5).
5) Введем зависимости из математической модели. Для этого в окне Поиск решения
установим целевую ячейку $B$15, установим направление изменения целевой функции, равное «минимальному значению», введем адреса изменяемых ячеек $B$3:$F$5, добавим ограничения: $A$3:$A$5=$A$11:$A$13; $B$6:$F$6=$B$10:$F$10 (см. рис.2
).
Рис. 2 - Ввод зависимостей из математической модели
6) Введем ограничения. Для этого в окне Параметры поиска решения
установим Линейная модель
и Неотрицательные значения.
Затем выполним поиск решения, нажав Выполнить
(см. рис.3
).
Рис. 3 - Установление параметров задачи
7) Просмотрим результаты и выведем отчет.
Таким образом, план перевозок примет вид:
- с 1-го карьера на 1-ый участок ремонта в объеме 150 ед., на 2-ой в объеме 250 ед. и на 4-ый в объеме 100 ед. (условных);
- с 2-го карьера на 2-ой участок ремонта в объеме 100 ед. и на 3-ий в объеме 200 ед. (условных);
- с 3-его карьера на 5-ый участок ремонта в объеме 100 ед. (условных).
Совокупные минимальные транспортные издержки составят 2300 у.е.
а)
Если появится запрет на перевозки от первого карьера до второго участка работ, то зависимости модели и решение задачи будут выглядеть следующим образом (см. рис.4,5
):

Рис. 4 - Ввод зависимостей из математической модели

Рис. 5 - Результаты решения
Таким образом, план перевозок примет вид:
- с 1-го карьера на 1-ый участок ремонта в объеме 150 ед., на 3-ий в объеме 150 ед., на 4-ый в объеме 100 ед. и на 5-ый участок 100 ед. (условных);
- с 2-го карьера на 2-ой участок ремонта в объеме 300 ед. (условных);
- с 3-его карьера на 2-ой участок ремонта в объеме 50 ед. и на 3-ий участок ремонта 50 ед. (условных).
Совокупные минимальные транспортные издержки составят 3100 у.е.
Отчет по результатам транспортной задачи имеет вид (см. рис.6
):

Рис. 6 - Отчет по результатам транспортной задачи
б)
Если по коммуникации от первого карьера до второго участка работ будет ограничен объем перевозок 3 тоннами, то зависимости модели и решение задачи примет вид (см. рис.7
):

Рис. 7 - Ввод зависимостей из математической модели
Таким образом, план перевозок примет вид:
- с 1-го карьера на 1-ый участок ремонта в объеме 150 ед., на 2-ой в объеме 3 ед., на 3-ий участок 147 ед., на 4-ый в объеме 100 ед. и на 5-ый участок 100 ед. (условных);
- с 2-го карьера на 2-ой участок ремонта в объеме 300 ед. (условных);
- с 3-его карьера на 2-ой участок ремонта в объеме 47 ед. и на 3-ий участок ремонта 53 ед. (условных).
Совокупные минимальные транспортные издержки составят 3088 у.е.
|