| Министерство Образования и Науки Украины
Харьковский национальный университет
А.А. Тензор, В.В. Невязкин
Краткий курс теории функции Зильберта
(на русском и украинском языках)
ТОМ 1
Харьков 2007
DFGKJH5676
Издание первое и последнее
© 2007 А.А. Тензор, В.В. Невязкин кафедра теории функции Зильберта
ОГЛАВЛЕНИЕ
:
| Математический анализ
|
|
4
|
| Линейная алгебра
|
|
5
|
| Дифференциальные уравнения
|
|
6
|
| Теоретическая механика
|
|
6
|
| Функциональный анализ
|
|
7
|
| Теория вероятности
|
|
8
|
| Комплексный анализ
|
|
9
|
| Дифференциальная геометрия
|
|
10
|
| Теория управления
|
|
14
|
| Численные методы
|
|
15
|
| Задачи
|
|
16
|
| Список использованной литературы
|
18
|
МАТАНАЛІЗ
Теорема
(Зільберта-Штольца)
Функція Зiльберта З(x
) має в околі точки x
похідні до (n
–1) порядку включно.
Доведення
(від приємного
)
. Припустимо, що З(x
) має похідні до (n
+8) порядку включно. Це дурниця.
Теорема
(Штрассермана)
Функція Штрассермана ШТР(x,з,ю) розкладається в ряд Тейлора з залишковим членом у вигляді функції Зільберта З(x
).
Доведення
.
Оскільки Функція Штрассермана досить приємна на вигляд, ми можемо записати нерівність:
ШТР(х,з,ю)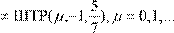
Отримали суперечність. Теорему доведено.
Зауваження 1
.
Ви спитаєте, при чому у попередній теоремі функція Зільберта? Відповідаємо – просто так!
Зауваження 2
.
Значення функції ШТР(π,з,ю) покладемо рівним πˆ (пі з дахом):
ШТР(π, ,з ю) ≡πˆ .
Якщо це не так, доповнимо інтеграл Пуассона порожніми брусами. Це корисна вправа.
Означення
.
Функція Штрассермана ШТР(x,з,ю), що діє на функцію Зільберта З(x
), називається оператором блабла
∇.
ЛІНІЙНА АЛГЕБРА
Твердження
Якщо ранг матриці Якобі J
дорівнює –1, та у тому випадку, коли власні вектори ортонормованого базису кореневого підпростору Зільберта
<α,β, ,γσ,...,χ1
,ω,ψ>
не усі нулі, можна записати тотожність:
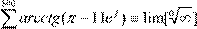 k
k
→1
j
=−9
Доведення
.
Приймемо цю теорему на віру.
Наслідки
Згідно до цієї теорії можна потрапити до лікарні.
ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
Означення
.
Матрицею Петросяна
називають матрицю П(x
), у якої елементи, що стоять на головній диагоналі, належать функції Зільберта З(x
).
Означення
.
Детермінант матриці Петросяна – петросяніан
П[З(x
)].
Теорема
(про замкненість петросяніана)
Якщо петросяніан задовольняє умовам теореми Зільберта-Штольца, і виконана достатня умова теореми Штрассермана, то петросяніан П[З(x
)] – замкнена множина на інтервалі [ , π-arctgμ], де μ – неперервна функція.
Доведення
.
Наш інтервал [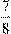 , π-arctgμ] – компакт ⇒ за теоре-
мою Вейєрштраса-Ляпунова, він має скінченне покриття. Спрямуємо μ на +∞ \{2} та підставимо правий кінець інтервала у петросяніан. Отримали:
П ,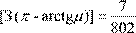
а це означає, що петросяніан – замкнена множина, оскільки
 ). Теорему доведено.
ТЕОРЕТИЧНА МЕХАНІКА
Принцип локалізації в’язей до (n-8) порядку включно
Якщо спочатку подивитися наліво, а потім направо, то, використовуючи метод віртуальних ітерацій, можемо найкоротшим шляхом прийти на схід.
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
Неравенство Треугольника
*
.
*Треугольник И.И. – выдающийся Харьковский математик, один из основателей теории функции Зильберта.
Теорема 1
Пусть α, ,b
ξ – стороны треугольника.
Тогда α+b
>ξ. (1)
Замечание
.
“> ” – знак “больше так сказать”
– это то же самое, что знак “>” в пространстве Римана, только в пространстве Штрассермана ШТРn
.
Теорема 2
В принятых обозначениях b
+ξ>α. (8)
Теорема 3
В принятых обозначениях α+ξ>b
. (9)
Доказательство теоремы 1
(от приятного).
Пусть это не так, то есть α+b
<ξ. (11)
Но это противоречит аксиоматике Зильберта, согласно которой все теоремы верны!
Упражнение
.
Теоремы 2,3 доказать самостоятельно.
ТЕОРИЯ ВЕРОЯТНОСТИ
В теории функции Зильберта существует сходимость “так сказать”, “как надо” и ”как не надо”, а именно:
Определение
.
Последовательность 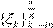 сходится “так сказать”
к числу ξ∈Z
(пространство Зильберта) ⇔ выполнены условия:
1. положим ξ=δ,
2. ∀ >ε 0 ∃δ: |ξk
−δ|>ε.
3. мат. ожидание функции Зильберта M[З(x)] равно константе Бернулли.
Обозначается ξk
⎯так
⎯⎯⎯⎯сказать
→ξ.
Определение
.
Последовательность 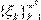 сходится “как надо”
к числу ξ∈Z:
ξk
⎯⎯→КН
⎯. .
ξ ⇔ дисперсия случайной величины ξk
равна интегралу Пуассона от трансцендентной функции.
Определение
.
Последовательность  сходится “как не надо”
к числу ξ∈Z:
ξk
⎯⎯ →К Н Н
.
⎯. .
ξ ⇔ дисперсия случайной величины ξk
равна нулю.
Определение
.
Функциональная последовательность f
(ξk
) ←
⎯
⎯⎯
⎯→
Λ
ξ λ→→
коллинеарно сходится
к Λ, когда ξ равномерно сходится к λ с
1
вероятностью  ⇔ f
'(ξk
) > 0, ∀k
: λ<k
<Λ.
k
КОМПЛЕКСНЫЙ АНАЛИЗ
Теорема
.
Рассмотрим конформное отображение f
из области D
в область G
:
D
а б в г д е ж з и к
1
2
3
4
5
6
7
8
9
10
f
: D
→ G
G
а б в г д е ж з и к
1
2
3
4
5
6
7
8
9
10
Тогда на ∀ факультете ∃ пара такая, что отображение f
∃ и не единственно, более того, таких отображений ∃ минимум два.
Проверить самостоятельно.
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
N-угольники в пространстве Зильберта
1. Регулярный одноугольник
Определение
.
Регулярный одноугольник
– геометрическая фигура, (
состоящая из вершины (точки A
) и дуги (AA
):
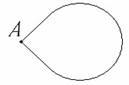
Теорема
(о длине дуги регулярного одноугольника)
Пусть γ – регулярный одноугольник с вершиной в точке A
. Возь(
мём точку B
∈γ, B
≠ A
. Тогда длина дуги AB
равна
( B
l AB
( ) =∫d
ξ.
A
Замечание
.
Если A
=B
, то длина дуги неопределена и условно
∞
считается равной  .
8
Упражнение
.
Доказать эту теорему самостоятельно.
2. Пространство двуугольников, измеримых по Зильберту
Определение
.
Двуугольник называется измеримым по Зильберту
, если у него 2 угла, причём один угол – первый, а другой – второй.
Примеры
1. Простой двуугольник
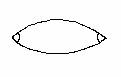
2. Прямой равноугольный двуугольник
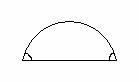
3. Прямоугольный двуугольник
Замечание
.
Двуугольники бывают выпуклые и впуклые, например
Теорема
Впуклые двуугольники измеримыми по Зильберту не являются. Это следует из основной предельной теоремы Зильберта-Остроградского.
Теорема
В пространстве Зильберта Zn
двуугольники, измеримые по Зильберту, можно дифференцировать, интегрировать и брать от них невязку ⇔ мат. ожидание косого геликоида, содержащего этот двуугольник, имеет предел, который сходится к константе Бернулли.
Доказательство
.
Клянусь Демидовичем!
3. Пространство треугольников, измеримых по Зильберту
Определение
.
Треугольник называется измеримым по Зильберту
, если сумма его углов больше 1800
.
Примеры
1. Треугольник Зильберта
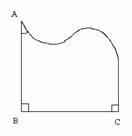
2. Треугольник Штрассермана (штреугольник) – имеет 3 прямых угла
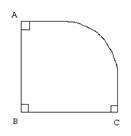
3. А этот треугольник не измерим по Зильберту
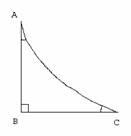
4. Классификация одноугольников
Одноугольники могут иметь 1, 2 или 3 вершины, если дуга незамкнута и имеет самопересечения.
Примеры
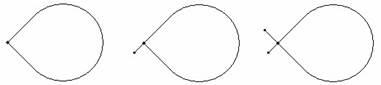
Замечание
.
Если число вершин >3, одноугольник называется вырожденным
. Точка тоже вырожденный случай. Такие одноугольники мы рассматривать не будем.
Пример
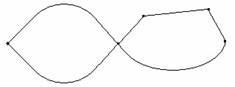
5. Шестиугольник ATBCEB
Теорема
.
Рассмотрим шестиугольник ATBCEB и расположим его стороны в порядке возрастания. Тогда сумма длин его сторон в пространстве Лобачевского, умноженная на cosecτ, где
τ∈ −( 4.7,18] – дискретная функция, которая принимает 2 значе-
ния: {1, 15} в зависимости от знака cosecτ.
Замечание
.
Эта теорема будет доказана на старших курсах.
ТЕОРИЯ УПРАВЛЕНИЯ
Определение 1
.
Последовательность  очень слабо сходится
к элементу ξ∈Z
(пространство Зильберта) ⇔ мы этого хотим слабо.
Определение 2
.
Последовательность  очень сильно сходится
к элементу ξ∈Z
⇔ мы этого хотим сильно.
Теорема
(Коклюшкина)
Определения 1 и 2 неэквивалентны.
Доказательство
.
Действительно, мы же не можем одновременно хотеть одного и того же слабо и сильно! Теорема доказана.
ЧИСЛЕННЫЕ МЕТОДЫ
Рассмотрим сумму с коэффициентами c
k
, где
k
−1
| f
c
k
= k
−1 k
|
k
−1
−∑
|
f
j
∏
i
=0 x
j
− x
i
i
≠ j
|
   x
n
− x
i
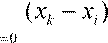 ∏(x
k
− x
l
) j
=0 
i
=0 i
и, пожалуй, хватит.
ЗАДАЧИ
1. Как доопределить остаточный член функции Зильберта в выколотой окрестности ∞, в точке {–6} так, чтобы относительно винтовой линии (n
–3) порядка cosϕ и sinϕ были параллельны?
(Ответ – молча)
2. (Прикладная задача мат. статистики) Берём константу Бернулли и устремляем её на 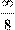 . Вопрос: как будет вести себя на беско-
нечности трансцендентная функция, умноженная на константу Бернулли? (Ответ – вызывающе)
3. Доказать, что в пространстве Зильберта Zn
числитель и знаменатель ортогональны, а их нормы и невязки скрещиваются.
4. Попробуйте на досуге проаппроксимировать функцию Зильберта З(x
) константами Бернулли.
5. Введём в рассмотрение функцию Бюншмана Б
(x
)
n
Б
( )x
= −|| f
∑c y
k k
||
k
=1
Вопрос: как теперь вывести её из рассмотрения?
6. Доказать, что у всех девушек волосы одного цвета. Решение (методом мат. индукции)
.
10
. При n
=1 утверждение верно: у одной девушки волосы одного цвета.
678k
678k
000...0014243 000...0014243
k
+1 k
+1
Рис. 1.
20
. Пусть утверждение верно при n
=k
. Докажем его для n
=k
+1. Внимательно рассмотрим k
+1 девушку. У первых k
девушек волосы одного цвета (по предположению), и у последних k
девушек волосы одного цвета, значит, у k
+1 девушки волосы одного цвета.
Утверждение доказано.
СПИСОК ИСПОЛЬЗОВАННОЙ
ЛИТЕРАТУРЫ
:
1. В учебнике по теории функции Зильберта использованы конспекты студентов мех-мата по:
- матанализу,
- линейной алгебре,
- диффурам,
- теормеху,
- функану,
- теорверу,
- комплану,
- дифф. геометрии,
- теории управления, - численным методам, где все имена и теоремы вымышленные, любое сходство с уже существующими случайно.
2. Демидович Б. П. “Сборник задач и упражнений по математическому анализу”.
Также здесь фигурируют фразы и выражения некоторых преподавателей с мех-мата, кто знает, тот поймёт.
Тираж 600 экземпляров.
Цена 20 коп.
|
