СОДЕРЖАНИЕ
ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛИ ЦП; ХАРАКТЕРИСТИКА И КЛАССИФИКАЦИЯ МЕТОДОВ ЦП
__________________________________________________________________________ 1
1.1 ПРЕДМЕТ ДО (ЦП) ___________________ Ошибка! Закладка не определена.
1.1.1 Предмет ДО ___________________________________________________________ 2
1.1.2 Классификация прикладных задач ________________________________________ 2
1.1.3 Классификация моделей ЦП _____________________________________________ 4
Задача о загрузке бомбардировщика (1955, США). _______________________________ 4
Задача о ранце (о контейнерах, о перевозках). ___________________________________ 4
Простейшая модель реконструкции. ___________________________________________ 5
Задача о развитии экономической зоны ________________________________________ 6
Задача о коммивояжере ______________________________________________________ 7
Задача о назначении_________________________________________________________ 8
Задачи теории расписаний (календарного планирования) _________________________ 8
Задача о покрытии _________________________________________________________ 10
Неоднородная ТЗ с фиксированными доплатами ________________________________ 10
Распределительная задача (обобщенная ТЗ) ____________________________________ 11
Распределительная задача с фиксированными доплатами ________________________ 12
Модель задачи выпуска продукции с разрывной целевой функцией ________________ 13
Модель многоэкстремальной задачи оптимизации ______________________________ 14
Задачи логического проектирования: задача о расположении производственных единиц14
1.2 КЛАССИФИКАЦИЯ ЧИСЛЕННЫХ МЕТОДОВ; ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ
МЕТОДОВ РЕШЕНИЯ ЗЦП_________________________________________________ 16
1.3 МЕТОДЫ ВЕТВЕЙ И ГРАНИЦ __________________________________________ 16
1.3.1 Схема метода ветвей и границ ___________________________________________ 16
1.3.2. Алгоритм Лэнда и Дойга _______________________________________________ 17
1.3.3 Алгоритм Литтла _____________________________________________________ 18 1.3.4 Схема алгоритма Литтла _______________________________________________ 19
1.4 МЕТОДЫ ОТСЕЧЕНИЯ. ПЕРВЫЙ АЛГОРИТМ ГОМОРИ ___________________ 21
1.4.1 Первый алгоритм Гомори ______________________________________________ 21
1.4.2 Алгоритм двойственного симплекс-метода ________________________________ 22 1.4.3 Геометрическая интерпретация первого алгоритма Гомори __________________ 22
1.5 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗЦП _____________________________ 23 1.5.1 Метод ближайшего соседа ______________________________________________ 23 1.5.2 Задача о контейнерных перевозках _______________________________________ 23
1.5.3 Метод Фогеля для решения задачи о назначении ___________________________ 24
1.6 ЗАДАЧИ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ С БУЛЕВЫМИ ПЕРЕМЕННЫМИ.
АДДИТИВНЫЙ МЕТОД БАЛАША __________________________________________ 25 1.6.1 Описание идеи аддитивного алгоритма ___________________________________ 26
1.6.2 Общая схема алгоритма Балаша _________________________________________ 26 1.6.3 Правила построения частичного решения _________________________________ 27
1.6.4 Алгоритм метода Балаша _______________________________________________ 28
1.6.5 Сведение ЗЦП в общей постановке к задаче с булевыми переменными ________ 29
1.7 ПРИБЛИЖЕННОЕ РЕШЕНИЕ. ИСПОЛЬЗОВАНИЕ ТОЧНЫХ МЕТОДОВ И ТОЧНОРЕШАЕМЫХ
ЗАДАЧ __________________________________________________________________ 29
1.7.1 Оценка качества приближенного решения291.7.2 Использование точно решаемых задач для получения приближенного решения31ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛИ ЦП; ХАРАКТЕРИСТИКА И КЛАССИФИКАЦИЯ МЕТОДОВ ЦП
1.1.1 Предмет ДО
ЦП–часть математического программирования, изучающие экстремальные задачи на конечных множествах или нецелочисленных решетках. В терминах ЦП формулируется широкий круг прикладных задач оптимизации, связанных с неделимостью, фиксированными доплатами, условиями логического типа, с наличием стандартов при проектировании, комбинаторные задачи.
ДП является одним из наиболее важных и сложных разделов МП. Интерес к дискретным экстремальным задачам определяется не только широким кругом приложений, но и органической связью инструментария реализации дискретных задач с другими разделами МП и математики.
Проблематика ДП связана с дискретной и целочисленной математикой (теория чисел, математическая логика, теория графов, теория конечных групп и др.), а также использует теорию ЛП, теорию двойственности, теорию численных методов, методов случайного поиска, методов имитационного моделирования. Прикладным аспектом ДП являются многие задачи экономики, планирования, управления, проектирования; в рамках ДП также формализуются задачи с логическими условиями, многоэкстремальные задачи. В качестве поля проблем при постановке задач ДП используются различные проблемы и процессы экономического оптимизационного характера.
Задачи ДО характеризуются в виде модели ЦП вида:

 Если f
( X
) , где X
( x
1
,..., x
n
) - нелинейная функция, то имеем нелинейную задачу ЦП (НЗЦП); если f
( X
) - линейная, то ЛЗЦП. Если f
( X
) , где X
( x
1
,..., x
n
) - нелинейная функция, то имеем нелинейную задачу ЦП (НЗЦП); если f
( X
) - линейная, то ЛЗЦП.
Прикладной аспект ДО рассматривает в основном ЛЗЦП вида:

Если последние ограничения накладываются на все j
, то задача полностью целочисленная, если на часть
j
, то частично целочисленная.
1.1.2 Классификация прикладных задач
Рассмотрим класс прикладных задач по источникам возникновения целочисленности.
Требования целочисленности компонент вектора X
вытекает из постановки задачи. Выделяют следующие основные источники целочисленности: 1) Задачи с неделимостями.
В таких задачах физическая неделимость единицы x
j
есть требование постановки, т.е. физическая сущность x
j
такова, что x
j
могут принимать только целочисленные значения. Это требование возникает в случаях, когда:
А) используемыми переменными являются крупные объекты (количество самолетов, турбин, заводов и т.д.)
Б) интерпретация результатов решения задачи такова, что требования целочисленности подразумевается априори. К таким постановкам относятся задачи, использующие в качестве интенсивности производства или распределения некоторые стандартные единицы – модули, комплексы машин и т.д.
Применение:
- задачи оптимизации средств в доставке грузов;
- задачи минимизации числа транспортных единиц для осуществления заданного графика перевозок;
- задачи минимизации порожнего пробега автомобилей при реализации заданного графика; - задачи оптимизации и комплектования стандартными модулями некоторого производства;
- И т.д.
2) Задачи размещения.
Постановка задачи предполагает выбор вариантов плановых решений из набора возможных таким образом, чтобы совокупность вариантов оптимизировала суммарный показатель качества.
Тогда формализация множества вариантов плановых решений для некоторого производственного объекта возможно только во множестве Z
.
Применение:
- задача планирования, развития и размещения производства;
- задача специализации; - задача кооперирования.
3) Комбинаторные задачи.
Данный тип прикладных задач делится на 2 класса:
- задачи, укладывающиеся в схему классической задачи о коммивояжере; - задачи теории расписаний.
Формальная схема постановки: найти путь минимальной длины проходящий раз и только раз через каждую вершину графа, непрерывный и заканчивающийся в исходной вершине.
Применение: задачи нахождения маршрутов развозки груза, минимизирующие пробег.
Формальная постановка задачи теории расписаний: упорядочить во времени использование системы машин для обработки некоторого множества изделий.
Применение: большинство задач организации производственного процесса.
4) Задачи о покрытии; задачи ДО сетей (другие комбинаторные задачи).
Формальная схема постановки задачи о покрытии: найти минимальное подмножество множества ребер данного графа, содержащего все вершины графа.
Применение:
- задача синтеза логических сетей;
- задачи синтеза оптимальных по стоимости, компактности, надежности и т.д. систем переработки информации (управляющих систем).
Формализация схемы постановки задачи ДО сетей: на сети определить разрез с минимальной пропускной способностью, т.е. максимизировать поток через данную сеть.
Применение:
- собственно задачи поиска максимального потока; - транспортная задача по критерию времени.
5) Особые задачи.
Задачи, в которых требование целочисленности в явном виде не входит, но имеются особые требования, относящиеся либо к функции цели, либо к ограничениям, которые выводят данный круг задач за рамки ЛП.
К таким задачам относятся:
- задачи с неоднородной функцией цели на выпуклом многограннике; - задачи, в которых ограничения содержат условия «либо-либо».
Тогда ОДР не является выпуклым многогранником и оказывается либо невыпуклой, либо не связанной областью (обычно объединение нескольких выпуклых многогранников). Такого рода задачи могут быть сведены к ЦЗП вида (2).
1.1.3 Классификация моделей ЦП
1) Модели задач с неделимостями.
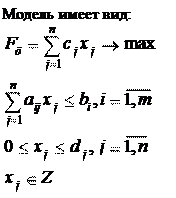
Приведем примеры постановок и моделей задач с неделимостями:
Задача о загрузке бомбардировщика (1955, США).
 Определить загрузку бомбардировщиков различных типов бомбовыми запасами, чтобы максимизировать суммарный эффект данной системы от боевых операций. Дано: i
1, m
- типы бомб, b
i
- запасы бомб, Определить загрузку бомбардировщиков различных типов бомбовыми запасами, чтобы максимизировать суммарный эффект данной системы от боевых операций. Дано: i
1, m
- типы бомб, b
i
- запасы бомб,
j
1, n
- типы самолетов, n
j
- суммарное число боевых вылетов,
k
1, p
- типы боевых операций, a
ik
- эффективность бомбы i
на операции k
, w
k
- «вес» операции, оп-
ределенный командованием. Найти:
x
ijk
- количество бомб типа i
, подлежащих загрузке в самолет типа j
при его использовании в операции
k
( в боковой бомбодержатель), y
ijk
- в центральный бомбодержатель.

Задача о ранце (о контейнерах, о перевозках).
 Имеется j
1, n
предметов веса a
j
ценностью c
j
. Задана грузоподъемность контейнера A
. Имеется j
1, n
предметов веса a
j
ценностью c
j
. Задана грузоподъемность контейнера A
.
Надо так загрузить контейнер предметами, чтобы суммарная стоимость их была максимальной при условии, что предмет может загружаться в количестве 1 штуки или не загружаться.
Обозначим переменные:
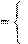 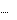 1, еслиберем jыйпредмет
, x
j 1, еслиберем jыйпредмет
, x
j
0, иначе
.
Модель:
 max max
Примечания:
- Если ограничений несколько, то будет многомерная задача;
- Если предмет может загружаться в нескольких экземплярах, но не больше d
j
, тогда вместо требования бивалентности будем иметь:
j
.
 x j x j
2) Модели задач размещения.
Простейшая модель реконструкции.
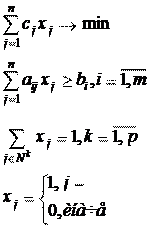 ûé âàðèàíò ïðèíÿò ûé âàðèàíò ïðèíÿò
  Данная модель реализует следующую постановку: предлагается j
1, n
- способов вариантов реконструкции каждого из k
1, p
предприятий, производящих i
1, n
видов продукции. Данная модель реализует следующую постановку: предлагается j
1, n
- способов вариантов реконструкции каждого из k
1, p
предприятий, производящих i
1, n
видов продукции.
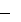 Заданы удельные в единицу времени (имеется ввиду отрезок планирования) выпуски продукции по способам a
ij
и приведены затраты на осуществление реконструкции по вариантам j
c
j
, N k
- множество номеров вариантов реконструкции предприятия k
. N k
не пересекаются, т.е. N S Заданы удельные в единицу времени (имеется ввиду отрезок планирования) выпуски продукции по способам a
ij
и приведены затраты на осуществление реконструкции по вариантам j
c
j
, N k
- множество номеров вариантов реконструкции предприятия k
. N k
не пересекаются, т.е. N S
 S
. S
.
Примечание. Если варианты в N k
пересекаются, то вводится двойная нумерация:
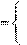 1, если реконструируетсяk приварианте j x
kj 1, если реконструируетсяk приварианте j x
kj
0, иначе
Выбрать такой набор вариантов реконструкции для совокупности предприятий числом p
, чтобы затраты на осуществление реконструкции были минимальными и при условии, что требуемый объем продукции i
будет произведен.
В случае, когда:
- речь идет не о реконструкции, а о основном строительстве, тогда в подмножестве номеров вариантов N k
будет только один- вариант строительства;
- задача размещения в этом случае осуществляется или не осуществляется строительство по вариан n n
ту k
. Тогда условие выбора единственного варианта 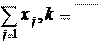 1, p
заменяется на 1, p
заменяется на 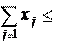 1 . 1 .
Приведенная задача не учитывает интересы потребителей (потребности предприятий и оптимизации транспортных потоков). Задачи, которые это учитывают называются производственно-транспортными.
3) Модели комбинаторных задач
Задача о развитии экономической зоны
Задача о развитии экономической зоны – это расширенная задача выбора проектных вариантов.
  Пусть имеется m
, i
1, m
предприятий вновь проектируемых или реконструируемых. Предприятия должны выпускать n
видов продукции j
1, n
в количествах не менее b
j
. Пусть имеется m
, i
1, m
предприятий вновь проектируемых или реконструируемых. Предприятия должны выпускать n
видов продукции j
1, n
в количествах не менее b
j
.
 Каждое из предприятий i
можно реконструировать по одному из заранее разработанных r
проектных вариантов k
1, r
(если количество вариантов для предприятий разное, то r Каждое из предприятий i
можно реконструировать по одному из заранее разработанных r
проектных вариантов k
1, r
(если количество вариантов для предприятий разное, то r
Каждый k
-ый вариант для предприятия i
характеризуется показателями величины выпуска продукции a
ij
k
по вариантам проектов и заданы приведенные затраты на осуществление проекта R
i
k
.
Требуется с минимальными затратами на строительство или реконструкцию предприятий удовлетворить потребности региона по всем видам продукции j
в объемах b
j
.

Задача о развитии экономической зоны – это задача выбора проектных вариантов, в которой планирование развития экономической зоны необходимо выполнить с учетом размещения пунктов потребления продукции и осуществления возможных объемов перевозок. Чтобы это реализовать, дополним постановку так:
  Пусть в регионе, представляющий собой совокупность n
городов ( i
1, m
) (предприятий), каждое предприятие может перевезти в другой город Пусть в регионе, представляющий собой совокупность n
городов ( i
1, m
) (предприятий), каждое предприятие может перевезти в другой город 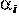 количество продукции. В регионе существуют j
1, n
предприятий, потребляющих однородную продукцию в количествах j
. количество продукции. В регионе существуют j
1, n
предприятий, потребляющих однородную продукцию в количествах j
.
Заданы затраты на перевозку c
ij
. Требуется так оптимизировать строительство и реконструкцию предприятий в зоне, чтобы суммарные затраты на строительство предприятий и транспортировку продукции были минимальны.
Введем переменную y
ij
-объемы перевозок предприятия i
к потребителю j
. Модель:

Получили частичную ЦЗП, которая решается, например, методом Балаша.
Модификациями транспортной задачи являются: ТЗ с ограниченными пропускными способностями коммуникаций, ТЗ с запретами.
Многие специальные ТЗ сводятся к классической ТЗ: ТЗ с перевалочными пунктами или с промежуточной обработкой, ТЗ с резервированием, ТЗ с дополнительными ограничениями.
К задачам транспортного типа относятся также задача о максимальном потоке и задача о кратчайшем пути. Они называются ТЗ в сетевой постановке.
Задача о коммивояжере
 Рассмотрим задачу о коммивояжере (КВ). Есть ( n
1) городов, c
ij
- матрица расстояний. Из города номер 0 выезжает КВ. Надо найти путь минимальной длины, проходящий раз и только раз через каждый город и заканчивался бы в нулевом. Рассмотрим задачу о коммивояжере (КВ). Есть ( n
1) городов, c
ij
- матрица расстояний. Из города номер 0 выезжает КВ. Надо найти путь минимальной длины, проходящий раз и только раз через каждый город и заканчивался бы в нулевом.
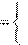 1, переходизiв jесть x
ij 1, переходизiв jесть x
ij
0, иначе
Модель:
 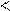 1) . 1) .
Полученное условие не справедливо, следовательно, условие замкнутости не позволяет затратить часть звеньев на подцикл.
Задача о назначении
 Если условие замкнутости отсутствует, то имеем модель о назначении – есть i
1, n
кандидатов на Если условие замкнутости отсутствует, то имеем модель о назначении – есть i
1, n
кандидатов на
 1, n
рабочих должностей, если i
-ый кандидат назначается на j
, то c
j
- затраты. Надо так провести все назначения, чтобы суммарные затраты были минимальными: 1, n
рабочих должностей, если i
-ый кандидат назначается на j
, то c
j
- затраты. Надо так провести все назначения, чтобы суммарные затраты были минимальными:
.
Задачи теории расписаний (календарного планирования)
  Задача календарного планирования относится к задачам теории расписания. Имеется m
, i
1, m
станков и n
, j
1, n
деталей. Задача календарного планирования относится к задачам теории расписания. Имеется m
, i
1, m
станков и n
, j
1, n
деталей.
Каждая деталь должна пройти обработку на m
станках в определенной последовательности, причем операции неделимы.
 Задана матрица A
a
ij i
j
1
1
,
,
m
n
, которая интерпретируется как время для обработки j
-ой детали на i
-ом станке. Задана матрица A
a
ij i
j
1
1
,
,
m
n
, которая интерпретируется как время для обработки j
-ой детали на i
-ом станке.
Надо найти такую последовательность обработки деталей, которая минимизировала бы продолжительность производственного цикла (общее время выполнения всех работ).
Введем обозначение x
ij
- моменты начала обработки j
-ой детали на i
-ом станке.
Тогда, календарный план есть совокупность элементов x
ij
, а продолжительность производственного цикла – общее время выполнения всех работ не складывается из x
ij
. Ограничения:
1) деталь проходит обработку в определенной последовательности. Пусть деталь j
сначала обрабатывается на станке i
в продолжительности времени a
ij
, а затем идет на станок k
.
 Тогда моменты начала обработки - x
kj
x
ij
a
ij
(1) Тогда моменты начала обработки - x
kj
x
ij
a
ij
(1)
Здесь возможны варианты:
- деталь ждет обработки на k
-ом станке, тогда 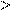
- деталь не ждет обработки 
-  при a
ij
0 деталь j
на i
-ом станке не обрабатывается по технологии. при a
ij
0 деталь j
на i
-ом станке не обрабатывается по технологии.
2) На одном станке нельзя одновременно обрабатывать две детали j
и s
. Моменты начала обработки двух деталей должны отстоять как минимум на длину обрабатывания детали, которая идет первой.
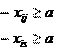 x
isij
( сначалаобрабатывается j
) x
isij
( сначалаобрабатывается j
)
Но мы не знаем, какая деталь идет первой, поэтому условия x
ijis
( сначалаобрабатывается s
) альтернативные, т.е. работает одно или другое.
Чтобы реализовать эту ситуацию введем дополнительную целочисленную переменную y
ijk
 . .
Обозначим верхнюю границу продолжительности производственного цикла через T
.
Тогда можно записать:
 T a
ij
1 y
ijs
x
is
x
ij
a
ij
(*) T a
is
y
ijs
x
ij
x
is
a
is
(**) x
is
x
ij
T T a
ij
1 y
ijs
x
is
x
ij
a
ij
(*) T a
is
y
ijs
x
ij
x
is
a
is
(**) x
is
x
ij
T
Исследуем данную конструкцию:
А) x
ij
x
is
0 . Ситуация невозможна, т.к. это означает одновременную обработку двух деталей на станке.
В (*) y ijs
0 , (**) y ijs
1 .
  Б) x
ij
x
is
0 , то (*) y
ijs
0 ; (**) y
ijs
{0,1} . Б) x
ij
x
is
0 , то (*) y
ijs
0 ; (**) y
ijs
{0,1} .
  Значит y
ijs
0 (единственное возможное значение). В) x
ij
x
is
0 , то (*) y
ijs
{0,1} ; (**) y
ijs
1 . Значит y
ijs
0 (единственное возможное значение). В) x
ij
x
is
0 , то (*) y
ijs
{0,1} ; (**) y
ijs
1 .
Значит y
ijs
1 (единственное возможное значение). Таким образом, формальная конструкция (*) и (**) реализует альтернативные условия.
 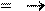 3) Момент окончания обработки на j 3) Момент окончания обработки на j
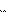 ой детали на i
-ом станке не превышает искомую длину производственного цикла t
: x
ij
a
ij
t
. Целевая функция задачи f t
min . Таким образом имеем модель: f
min ой детали на i
-ом станке не превышает искомую длину производственного цикла t
: x
ij
a
ij
t
. Целевая функция задачи f t
min . Таким образом имеем модель: f
min
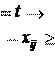 x
kj
a
ij x
kj
a
ij

Вследствие большого разнообразия производственных условий возможностей производства универсальная постановка задачи календарного планирования невозможна.
Приведенная постановка является наиболее простой.
Ограничения задачи могут быть дополнены следующими:
- условиями на сроки окончания отдельных работ;
- требование учета различных проиводственных факторов (труд, материалы, оборудование);
- требование учета дополнительных производственных факторов, сопровождающих процесс производства – особенностей технологии.
В качестве критериев оптимальности в этой задаче может быть использованы и другие критерии, которые делятся на 2 группы:
1) критерии, зависящие от общей продолжительности обработки изделий. К ним относятся: минимум простоев оборудования; максимум показателя использования оборудования; минимум издержек на незавершенное производство
2) критерии, которые являются функцией заданных сроков готовности: минимум суммарного отставания от сроков; минимум издержек, связанных с невыполением работ в срок; минимум числа отстающих работ.
4) Модель задачи о покрытии.
Задача о покрытии
Общий вид: n
c j
x j
min
j
1 n
a ij
x j
b i
, i
1, m
j
1
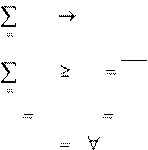 x j
{0,1}, a ij
{0,1} x j
{0,1}, a ij
{0,1}
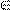 Если c
j
1, j
, то простая задача о покрытии; если c
j
R
, то взвешенная задача о покрытии. Если c
j
1, j
, то простая задача о покрытии; если c
j
R
, то взвешенная задача о покрытии.
Описание конкретных постановок задач о покрытии проводится на логическом языке в терминах синтеза схем с использованием булевых функций, связывающих входы и выходы устройства.
Тогда задачей синтеза является построение схемы, реализующей дополнительную булеву функцию, затем среди полученной совокупности схем выбираются в соответствии с заданным критерием. 5) Особые задачи.
Неоднородная ТЗ с фиксированными доплатами
В качестве задачи с разрывной функцией цели рассмотрим ТЗ с фиксированными доплатами или неоднородную ТЗ.
 Постановка: i
1, m
- пункты производства, a
i
- объемы производства; j
1, n
- пункты назначения, b
i
- потребности. Постановка: i
1, m
- пункты производства, a
i
- объемы производства; j
1, n
- пункты назначения, b
i
- потребности.
Кроме того, по условиям перевозки требуется дополнительно платить d
ij
ден.ед. независимо от величины груза в случае, если груз перевозится из i
в j
.
Интерпретация доплаты d
ij
может быть: плата за аренду авто, дорожный сбор на крупных дорожных сооружениях, таможенная политика и т.д.
Модель. В связи с новыми условиями целевая функция ТЗ становится принципиально другой. Это функция, в которой прежнее c
ij
становится зависимой от того, перевозится груз или нет.

Здесь переменных целочисленных нет.
 Чтобы численно реализовать такую модель сведем ее к ЧЦЗ. - определим величины M
ij
min{ a
i
, b
j
} i
, j Чтобы численно реализовать такую модель сведем ее к ЧЦЗ. - определим величины M
ij
min{ a
i
, b
j
} i
, j
- 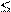 введем переменные y
ij
{0,1} и условия x
ij
M
ij
y
ij
. введем переменные y
ij
{0,1} и условия x
ij
M
ij
y
ij
.
m n
Тогда F
( c
ij
x
ij
d
ij
y
ij
) .
i
1 j
1
Рассмотрим, как работает в оптимальном плане:
- если y
ij
0 , то x
ij
0 ;
- если y
ij
1 , то x
ij
M
ij
неравенство излишнее (по построению);
-  если x
ij
0 , то y
ij
должен быть нулем, иначе план не оптимальный и его можно улучшить; - Если x
ij
0 , то y
ij
1 . если x
ij
0 , то y
ij
должен быть нулем, иначе план не оптимальный и его можно улучшить; - Если x
ij
0 , то y
ij
1 .
Таким образом, переменные y
ij
{0,1} «согласуют» плату за аренду и действие – осуществление перевозки.
В схему ТЗ с фиксированными доплатами укладывается также задача о смесях, имеющие фиксированные доплаты (фиксированная стоимость заказа, компоненты смеси, не зависящие от заказываемого количества).
Распределительная задача (обобщенная ТЗ)
 Рассматривается транспортное предприятие с j
1, n
транспортными линиями (маршрутами). В соответствии с планом графика по j
-ой линии надо выполнить b
j
рейсов. Рассматривается транспортное предприятие с j
1, n
транспортными линиями (маршрутами). В соответствии с планом графика по j
-ой линии надо выполнить b
j
рейсов.
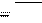 Фонд наличных транспортных средств (транспортный парк) представлен i
1, m
типами транспортных единиц с полными резервами времени a
i
. Фонд наличных транспортных средств (транспортный парк) представлен i
1, m
типами транспортных единиц с полными резервами времени a
i
.
Заданы затраты времени на выполнение i
-ой транспортной единицей рейса j
- t
ij
и затраты денежных средств c
ij
.
Надо оптимизировать расстановку транспортных единиц по рейсам так, чтобы суммарные затраты были минимальными.
Введем обозначение: x
ij
- количество i
-го транспорта на j
-ом маршруте.
Модель:
 (2) (2)
(3)
(4)
Распределительная задача с фиксированными доплатами
Пусть дополнительно в постановке обобщенной ТЗ нужно учесть следующее: выпуск транспортных средств i
на маршрут j
связан с дополнительными затратами времени 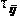 , не зависящие от числа рейсов, и денежных средств d
ij
. , не зависящие от числа рейсов, и денежных средств d
ij
.
Тогда затраты средств c
ij
будут зависеть от того, будет ли транспортное средство i
содержать хотя бы один рейс по маршруту j
или нет.
Таким образом: c
ij
(5)
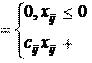 d
ij
, x
ij d
ij
, x
ij
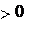
Аналогично, для затрат времени: t
ij
( x
ij
) 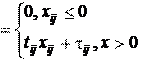 (6) (6)
Получили модель:

Отличие данной задачи с задачей с фиксированными доплатами в том, что фиксированные доплаты входят не только в целевую функцию, но и в ограничения.
Сведение (7)-(10) к ЗЦП основано на использовании верхних границ для переменных x
ij
- M
ij
.
Найдем эти границы:
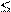 А) из (9) имеем x
ij
b
j А) из (9) имеем x
ij
b
j

времени и определять был или не был совершен рейс. Получили модель:
 (15) (15)
(16)
Модель задачи выпуска продукции с разрывной целевой функцией
Одним из источников возникновения дискретности является разрывная целевая функция.
Пусть x
j
- объем выпускаемой продукции типа j
, c
j
- прибыль за комплект продукции j
.
Предполагается, что прибыль получается только за готовые комплекты, отвечающие целочисленным значениям x
j
.
a
ij
- удельные затраты ресурса на 1 ед. продукции.
Максимизировать прибыль для описанного производства.

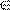 Сведем задачу к частично целочисленной. Введем дополнительные целочисленные z
j
Z
, которые ин- Сведем задачу к частично целочисленной. Введем дополнительные целочисленные z
j
Z
, которые ин-

Модель многоэкстремальной задачи оптимизации
Многоэкстремальную задачу можно рассматривать как задачу оптимизации с линейным целевым функционалом и с невыпуклой или несвязной областью определения.
Такую область можно точно или приближенно представить в виде объединения конечного числа выпуклых областей (при линейных ограничениях – выпуклых многогранниках).
Затем вводя целочисленные переменные свести задачу к частично целочисленной.
 Пусть невыпуклая область M
представляет собой объединение многогранников M
M
1
M
2
. Каждый из многогранников описывается системой ограничений: Пусть невыпуклая область M
представляет собой объединение многогранников M
M
1
M
2
. Каждый из многогранников описывается системой ограничений:

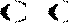 Обозначим левые части через g
1
x
, g
2
x
. Обозначим левые части через g
1
x
, g
2
x
.
Пусть известно число b
, для которого справедливо:
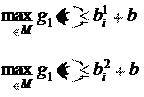 X X
, т.е. найдены верхние границы.
X
 Сведем задачу к ЧЗЦП, вводя y
{0,1} . Сведем задачу к ЧЗЦП, вводя y
{0,1} .
 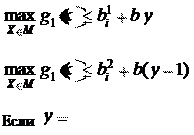 0 , то работаем во второй области, y
1 в первой. Т.о., через y
«связали» невыпуклую область. 0 , то работаем во второй области, y
1 в первой. Т.о., через y
«связали» невыпуклую область.
Задачи логического проектирования: задача о расположении производственных единиц
Задачи логического проектирования – самое молодое направление ЛП. Его применение связано с вопросами проектирования логических устройств, связанных с теорией кибернетики дискретного анализа.
 Задача о расположении произодственных единиц: имеется i
1, m
производственных единиц, или центров. Карта возможного расположения центров имеет j
1, n
мест. Заданы затраты, связанные с помещением центра i
на место j
- затраты на установку c
ij
. Задача о расположении произодственных единиц: имеется i
1, m
производственных единиц, или центров. Карта возможного расположения центров имеет j
1, n
мест. Заданы затраты, связанные с помещением центра i
на место j
- затраты на установку c
ij
.
Известны также затраты, связанные с перемещиеним i
на место j
, называюся «расстоянием» - d
ij
. Кроме этого заданы производственные потоки по пути ( i
, j
) - f
ij
. Целью задачи является закрепление центров по местам, минимизирующие суммарные затраты.
 Пусть mn
. Пусть mn
.
Модель: каждое назначение центров по местам представляет собой перестановки чисел 1,..., n
. Для каждого назначения заданы:
1) затраты, зависящие от назначения i
на место p
i
,( p
1
, p
2
,..., p
n
) c
ip
i
(непосредственные затраты) 2) затраты, зависящие от пар назначений (затраты на взаимосвязь центров) d
p
i
p j
.
Причем затраты при перемещении центра i
в место p
i
и центра j
в место p
j
равны произведению f
ij
на d
p
i
p
j
.
 Таким образом, в соответствие с постановкой, чтобы реализовать функцию цели нужно найти перестановку p
1
, p
2
,..., p
n
чисел от 1 до n
, минимизирующие суммарные затраты на назначение и взаимосвязь центров. Таким образом, в соответствие с постановкой, чтобы реализовать функцию цели нужно найти перестановку p
1
, p
2
,..., p
n
чисел от 1 до n
, минимизирующие суммарные затраты на назначение и взаимосвязь центров.
 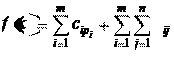 f d p
i
p j
min f d p
i
p j
min
 Примечание. В случае, когда производственная единица может быть помещена не в любое место, а лишь в одно из мест заданного списка S
i
, появляются ограничения p
i
S
i
, i
1, m
. Примечание. В случае, когда производственная единица может быть помещена не в любое место, а лишь в одно из мест заданного списка S
i
, появляются ограничения p
i
S
i
, i
1, m
.
Задача является экстремально-комбинаторной. Сведем ее к ЗЦП введя допущения:
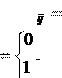 1) производственные центры не зависят друг от друга, т.е. f
0 . 1) производственные центры не зависят друг от друга, т.е. f
0 .
Введем переменные x
ij
- центр i
помещен на место j
: x
ij

Таким образом, получили задачу о назначении.
  Пусть в некоторой задаче МП помимо обычных условий есть условия вида h
1
( x
1
,..., x n
)0, h
2
( x
1
,..., x n
)0 (**) Пусть в некоторой задаче МП помимо обычных условий есть условия вида h
1
( x
1
,..., x n
)0, h
2
( x
1
,..., x n
)0 (**)
  h
1
, h
2
-заданные линейные функции; известны верхняя и нижняя границы h
1
( h
1
, h
1
) и нижняя граница h
2
h
2
. h
1
, h
2
-заданные линейные функции; известны верхняя и нижняя границы h
1
( h
1
, h
1
) и нижняя граница h
2
h
2
.
Действуют так:
 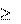 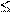  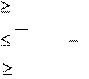 Условия (**) перепишем в виде: либо
h
1
( x
) 0, h
2
( x
)0, либо
h
1
( x
)0 Вводим переменную y
{0,1} . Запишем условия в виде: h
1
( x
) h
1
( x
) y h
1
( x
) h
1
( x
)(1 y
) . Условия (**) перепишем в виде: либо
h
1
( x
) 0, h
2
( x
)0, либо
h
1
( x
)0 Вводим переменную y
{0,1} . Запишем условия в виде: h
1
( x
) h
1
( x
) y h
1
( x
) h
1
( x
)(1 y
) .
h
2
( x
) h
2
( x
) y
Записанная система неравенств не содержит логических условий и реализует условия «либо-либо». Кроме рассмотренных, к особым относятся задачи многоэкстремальные на незамкнутых ОДР с разрывными функциями цели другого рода и другие.
1.2 КЛАССИФИКАЦИЯ ЧИСЛЕННЫХ МЕТОДОВ; ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ МЕТО-
ДОВ РЕШЕНИЯ ЗЦП
Все методы делятся на точные и приближенные. Точные методы делятся на 2 основные группы:
1) методы, основанные на идеях направленного перебора вариантов – методы ветвей и границ (Лэнд и Дойг, Литтл);
2) методы, суть которых состоит в численной реализации ЗЦП с дополнительным условием – правильного отсечения. Это методы отсечения (алгоритм Гомори). Методы ветвей и границ
Общая схема метода состоит в двухэтапном решении задачи. На первом этапе производится поиск экстремума функции цели на расширенной ОДР. На втором этапе последовательное пошаговое уточнение решения первого этапа.
Идея метода состоит в усовершенствовании процесса перебора вариантов. Сокращение числа вариантов достигается за счет того, что удается оценить сверху значение функции цели на разбиениях расширенного множества допустимых решений и затем исключить из рассмотрения те разбиения, для которых оценка оказалась слишком малой.
Оценки называются границами, а поиск решения проводится по ветвям дерева вариантов.
Методы отсечений
Методы отсечений используют 2 идеи: пошаговую линейную аппроксимацию ЗЦП, переход от шага к шагу с помощью правильного отсечения.
Общая схема метода такова:
Рассматривается ЗЛП, соответствующая исходной ЗЦП. ОДР для нее - выпуклый многогранник. Совокупность целочисленных точек в нем является множеством допустимых решений задачи и не является выпуклым. К ограничениям ЗЦП последовательно добавляются новые – они связывают внешние целочисленные точки последовательных решений.
В результате на каждом шаге получается новый выпуклый многоугольник, представляющий собой ОДР для новой ЗЦП. При это, вершина, соответствующая нецелочисленному решению отсекается. За конечное число шагов мы придем к вершине, координаты которого целочисленные.
1.3 МЕТОДЫ ВЕТВЕЙ И ГРАНИЦ
1.3.1 Схема метода ветвей и границ
 1) Итераций K
0 . Для расширенной ОДР X
(0)
полученной из исходной X
исключением части ограничений определяется максимальное значение целевой функции задачи: f
( x
) max, x X
(1). 1) Итераций K
0 . Для расширенной ОДР X
(0)
полученной из исходной X
исключением части ограничений определяется максимальное значение целевой функции задачи: f
( x
) max, x X
(1).
 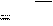 Обозначим максимальное значение f
( x
) f
( x
0
) . Это значение одновременно является верхней границей функции цели на исходном множестве допустимых планов: M
( X
) f
( x
0 ), x
0 X
(0) (2). Обозначим максимальное значение f
( x
) f
( x
0
) . Это значение одновременно является верхней границей функции цели на исходном множестве допустимых планов: M
( X
) f
( x
0 ), x
0 X
(0) (2).

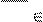 Если при этом план x
(0)
удовлетворяет исходному множеству допустимых планов x
(0)
X
, то процесс Если при этом план x
(0)
удовлетворяет исходному множеству допустимых планов x
(0)
X
, то процесс

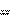 решения задачи (1) закончен и x
(0)
- искомое решение. 2) K
1,2,... решения задачи (1) закончен и x
(0)
- искомое решение. 2) K
1,2,...
 В соответствии с выбранным способом, отвечающим специфике задачи (1) производится разбиение перспективного подмножества допустимых планов (для K
1 такое подмножество одно, это X
(0)
) на непересекающиеся подмножества: В соответствии с выбранным способом, отвечающим специфике задачи (1) производится разбиение перспективного подмножества допустимых планов (для K
1 такое подмножество одно, это X
(0)
) на непересекающиеся подмножества:
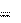 X
r
( k
) , r
0,..., r
k
: X
t
( k
) X
r
( k
) , r
0,..., r
k
: X
t
( k
) 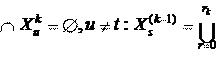 X
sr
( k
) (3) X
sr
( k
) (3)
r
-индекс подмножества, s
- идентификатор множества предыдущего шага.
Причем известно, что в X
s
0
оптимальных решений нет.
Помня, что в формуле (3) должен быть двойной индекс для дальнейшего упрощения изложения опустим его.
  Тогда оценки M
( x
r
( k
)
), r
1, k
ищутся как максимумы целевой функции на подмножествах X
r
( k
) , r
1, r
k
. Тогда оценки M
( x
r
( k
)
), r
1, k
ищутся как максимумы целевой функции на подмножествах X
r
( k
) , r
1, r
k
.
 Если план x
l
( k
)
, приносящий максимум f
( x
) на некотором подмножестве X
l
( k
)
одновременно удовлетворяет исходной системе ограничений x
l
( k
)
X
и является решением на итерации K
, то этот план является претендентом на решение исходной задачи. Если план x
l
( k
)
, приносящий максимум f
( x
) на некотором подмножестве X
l
( k
)
одновременно удовлетворяет исходной системе ограничений x
l
( k
)
X
и является решением на итерации K
, то этот план является претендентом на решение исходной задачи.
3) В процессе решения задачи подмножество X
0
увеличивается за счет включения в него X
t
( k
)
в следующих случаях:
а) если в результате сравнения оценок на разбиениях внутри итерации K
хотя бы для одного подмноже-

 ства X
r
( k
)
максимум f
( x
) на подмножестве X
t
( k
)
меньше максимума f
( x
) на подмножестве X
r
( k
)
: ства X
r
( k
)
максимум f
( x
) на подмножестве X
t
( k
)
меньше максимума f
( x
) на подмножестве X
r
( k
)
:
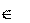 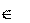 X t
( k
)
X
0
: M
( X
t
( k
)
) M
( X
r
( k
)
), t
, r R
( k
)
, где
R
( k
)
- подмножество индексов разбиений на итерации K
. X t
( k
)
X
0
: M
( X
t
( k
)
) M
( X
r
( k
)
), t
, r R
( k
)
, где
R
( k
)
- подмножество индексов разбиений на итерации K
.
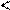 б) если в результате сравнения оценок между итерациями K
, P
, KP
хотя бы для одной итерации б) если в результате сравнения оценок между итерациями K
, P
, KP
хотя бы для одной итерации

 P
найдется такое подмножество X
l
( p
)
, что максимум f
( x
) на подмножестве X
t
( k
)
меньше максимума f
( x
) на подмножестве X
l
( p
)
, т.е. P
найдется такое подмножество X
l
( p
)
, что максимум f
( x
) на подмножестве X
t
( k
)
меньше максимума f
( x
) на подмножестве X
l
( p
)
, т.е.
  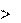 X
tk
X
0 : M
( X
l
( p
) ) M
( X
tk
), t R
( k
) , l R
( p
) , p k
1,...,1 X
tk
X
0 : M
( X
l
( p
) ) M
( X
tk
), t R
( k
) , l R
( p
) , p k
1,...,1
Ветви, включенные в X
0
являются тупиковыми.
4) Решением задачи (1) является лучшее из решений-претендентов; если в результате разбиения последнее подмножества процесса решения оказалось пустым и решений-претендентов нет, то исходная задача (1) целочисленных решений не имеет.
Процесс решения задачи (1) с использованием методов ветвей и границ иллюстрируется так называемым деревом ветвлений.
Для реализации описанной выше схемы в виде конкретного алгоритма необходимо указать:
- способ расширения ОДР;
- правило ветвления (разбиения на подмножества); - правило вычисления границ (оценок).
1.3.2. Алгоритм Лэнда и Дойга
Алгоритм применяется для решения частично целочисленных задач. Конкретизация алгоритма в соответствии с схемой метода ветвей и границ следующая:
1) способ расширения ОДР.
В качестве расширения X
(0)
исходной области ограничений X
используют область ограничений ЗЛП, соответствующая исходной ЗЦП. 2) правило ветвления.
   Пусть X
s
( k
1)
- перспективное подмножества шага k
1 . Разбиение его на подмножества X
sr
( k
)
, r
1, r
k
производится по правилам: Пусть X
s
( k
1)
- перспективное подмножества шага k
1 . Разбиение его на подмножества X
sr
( k
)
, r
1, r
k
производится по правилам:
-  из плана x
s
( k
1)
выбирается нецелочисленная компонента x
*
j
; из плана x
s
( k
1)
выбирается нецелочисленная компонента x
*
j
;
-  из ОДР, соответствующей этому плану x
s
( k
1)
исключается значения x
*
j
, лежащие в промежутке: ([ x
* j
];[ x
* j
] 1) . Таким образом, при разбиении X
s
( k
1) получаем два подмножества X
1( k
) , X
2( k
) , где: из ОДР, соответствующей этому плану x
s
( k
1)
исключается значения x
*
j
, лежащие в промежутке: ([ x
* j
];[ x
* j
] 1) . Таким образом, при разбиении X
s
( k
1) получаем два подмножества X
1( k
) , X
2( k
) , где:
X
1
( k
) { x
1
( k
) : x
1
( k
) X s
( k
1) , x j
[ x
* j
]},
 . (4) X
2
( k
) { x
2
( k
) : x
2
( k
) X s
( k
1) , x j
[ x
* j
] 1} . (4) X
2
( k
) { x
2
( k
) : x
2
( k
) X s
( k
1) , x j
[ x
* j
] 1}
Если оценки на некоторых подмножествах предыдущего шага одинаковы, то просматриваются все эти ветви с целью получения альтернативного решения. 3) Правило вычисления границ (оценок).
 Способ разбиения множеств на подмножество на каждом шаге K
0 генерирует две ЗЛП с целевыми функциями исходной задачи (1) и ОДР X
1
( k
)
, X
2
( k
)
. Способ разбиения множеств на подмножество на каждом шаге K
0 генерирует две ЗЛП с целевыми функциями исходной задачи (1) и ОДР X
1
( k
)
, X
2
( k
)
.
 Границами
M
( X
1
( k
)
), M
( X
2
( k
)
) являются максимальные значения исходной целевой функции на соответствующих ОДР f
( x
r
( k
) ), r
1, r
k
. Границами
M
( X
1
( k
)
), M
( X
2
( k
)
) являются максимальные значения исходной целевой функции на соответствующих ОДР f
( x
r
( k
) ), r
1, r
k
.
 Примечание 1
. Если коэффициенты функции цели при переменных, на которые накладываются условия целочисленности целые, а при остальных равны нулю, то оценку можно усилить: Z
r
( k
) ] f
( x
r
( k
) )[, r
1, r
k
. Здесь ] [ - наименьшее целое, не меньшее Примечание 1
. Если коэффициенты функции цели при переменных, на которые накладываются условия целочисленности целые, а при остальных равны нулю, то оценку можно усилить: Z
r
( k
) ] f
( x
r
( k
) )[, r
1, r
k
. Здесь ] [ - наименьшее целое, не меньшее 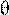 . .
Примечание 2.
При построении дерева ветвлений можно следовать по ветвям, приводящим к скорейшему получению 1-го претендента по решению исходной задачи – схема одностороннего обхода дерева. Ветви, не включенные в обход называются оборванными; их оценка вычисляется после первого рекорда. По другой схеме просматриваются и производятся ветвления одновременно по всем подмножествам итерации K
.
Первый способ ветвления предпочтительнее, т.к. он нагляднее в интерпретации и экономичнее при программировании метода.
В вычислительном аспекте алгоритм Л. и Д. сводится к решению серий ЗЛП. Конечность алгоритма обеспечивается тем, что исходное множество дополнительных планов ограничено.
Альтернативные решения ищутся в том случае, если в условии задачи его требовалось найти.
1.3.3 Алгоритм Литтла
Алгоритм Литтла укладывается в схему методов ветвей и границ и предназначен для решения прикладных задач ЦП специальной структуры.
Классической постановкой такой задачи является задача о коммивояжере, алгоритм решения которой в терминах теории графов можно сформулировать так:
Среди множества допустимых гамильтоновых контуров (ГК) выбрать контур минимальной длины. Алгоритм Литтла реализует схему направленного частичного перебора вариантов ГК. Конечность алгоритма следует из конечного числа ГК в допустимой области рассматриваемой задачи.
Определим основные положения алгоритма Литтла (АЛ) построения его как метода ветвей и границ. 1) Способ расширения ОДР.
 Для расширения исходной области ограничений X
опускается ограничение замкнутости маршрута. В результате получим область ограничения в задаче о назначении. В качестве матрицы затрат применяется матрица рассмотренной задачи о КВ, приведенная по строкам и столбцам C
(0)
C
'' . 2) Правила ветвления. Для расширения исходной области ограничений X
опускается ограничение замкнутости маршрута. В результате получим область ограничения в задаче о назначении. В качестве матрицы затрат применяется матрица рассмотренной задачи о КВ, приведенная по строкам и столбцам C
(0)
C
'' . 2) Правила ветвления.
   Принцип деления для каждого из подмножеств X
r
( k
)
, r
0, r
k
следующий: фиксируется дуга ( i
0
, j
0
) наименьшей длины. По этой дуге исходное множество ГК разбивается на 2 подмножества: 1) X
i
(
0
k
j
0
)
, составленное из ГК, содержащих дугу ( i
0
, j
0
) ; 2) X
i
(
0
k
j
0
)
, составленное из ГК, не содержащих дугу ( i
0
, j
0
) . Требование включения или не включения i
0
, j
0
в подмножество ГК реализуется путем соответствующих преобразований матрица, рассмотренной для подмножеств X
r
( k
)
, r
0, r
k
. Принцип деления для каждого из подмножеств X
r
( k
)
, r
0, r
k
следующий: фиксируется дуга ( i
0
, j
0
) наименьшей длины. По этой дуге исходное множество ГК разбивается на 2 подмножества: 1) X
i
(
0
k
j
0
)
, составленное из ГК, содержащих дугу ( i
0
, j
0
) ; 2) X
i
(
0
k
j
0
)
, составленное из ГК, не содержащих дугу ( i
0
, j
0
) . Требование включения или не включения i
0
, j
0
в подмножество ГК реализуется путем соответствующих преобразований матрица, рассмотренной для подмножеств X
r
( k
)
, r
0, r
k
.
3) Правила вычисления границ (оценок)
Оценкой снизу на X
(0)
является константа приведения исходной матрицы расширений C
.
Действительно, не сложно показать, что длина пути на C
равна длине пути на C
" (матрица, приведенная по строкам и столбцам) с константой приведения.
 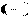 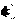 Поэтому, отбрасывая длину пути на C
" получаем нижнюю границу длин ГК на X
(0)
m
( X
0
) . В качестве оценки снизу подмножества X
r
берется сумма оценки исходной для X
r
k
множества – пусть это X
r
k
1
и константа приведения матрицы расширений, соответствующей подмножеству X
r
k
m
X
r
k
и трансформированной с учетом требования замкнутости мар шрута:
m
X
r
k
m
X
r
k
1
m
r
k
, r
1, r
k
. Поэтому, отбрасывая длину пути на C
" получаем нижнюю границу длин ГК на X
(0)
m
( X
0
) . В качестве оценки снизу подмножества X
r
берется сумма оценки исходной для X
r
k
множества – пусть это X
r
k
1
и константа приведения матрицы расширений, соответствующей подмножеству X
r
k
m
X
r
k
и трансформированной с учетом требования замкнутости мар шрута:
m
X
r
k
m
X
r
k
1
m
r
k
, r
1, r
k
.
Для контроля некоторого состояния маршрута дополнительно вводятся множества P
r
k
, P
r
k
, r
1, r
k
соответственно множество дуг входящих и не входящих в маршрут по ветви r
шага k
.
Учитывая факт, что АЛ использует специальный математический аппарат, приведем для него детальное описание схемы ветвей и границ с интерпретацией действий в терминах теории графов.
1.3.4 Схема алгоритма Литтла
1) Итерация K
0
 А: на X
0
по исходной матрице расстояний ищется нижняя граница всех ГК как константа приведения n n А: на X
0
по исходной матрице расстояний ищется нижняя граница всех ГК как константа приведения n n
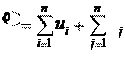 матрицы C
: m
0
min C ij
min C
' ij
или m v
, где C
' -матрица, приведенная матрицы C
: m
0
min C ij
min C
' ij
или m v
, где C
' -матрица, приведенная
i
1 j
j
1 i
по строкам.
  Б: Прежде чем перейти к шагу K
1 по C
" определяется дуга разбиения 1-го наша i
0
, j
0
1
. Б: Прежде чем перейти к шагу K
1 по C
" определяется дуга разбиения 1-го наша i
0
, j
0
1
.
    При выборе i
0
, j
0
1
логика размышлений такова: нужно стремиться к тому, чтобы множество ГК, включающее дугу X
i
0 1 j
0 содержало оптимальный контур, а X
i
0 1 j
0 не содержало. Поэтому в X
i
0 j
0 нужно включать дуги матрицы C
" с нулевым расстоянием. Одновременно в X
i
0
1
j
0
должны оставаться дуги с наибольшим расстоянием. При выборе i
0
, j
0
1
логика размышлений такова: нужно стремиться к тому, чтобы множество ГК, включающее дугу X
i
0 1 j
0 содержало оптимальный контур, а X
i
0 1 j
0 не содержало. Поэтому в X
i
0 j
0 нужно включать дуги матрицы C
" с нулевым расстоянием. Одновременно в X
i
0
1
j
0
должны оставаться дуги с наибольшим расстоянием.
      Последнее требование формализуется следующим образом: по определению, X
i
0
1
j
0
не содержит дугу i
0
, j
0
, т.е. для любого ГК путь из i
0
приводит в любую j Последнее требование формализуется следующим образом: по определению, X
i
0
1
j
0
не содержит дугу i
0
, j
0
, т.е. для любого ГК путь из i
0
приводит в любую j
 j
0
, а в j
0
приводит из i
i
0
. При этом длина дуги пути будет не меньше, чем так называемая степень нулевого элемента: ij i
o
j i i
0 ij
0 . Здесь R
0 - множество дуг матрицы C
, имеющих нулевое рас min C
min C
, i
, j j
0
, а в j
0
приводит из i
i
0
. При этом длина дуги пути будет не меньше, чем так называемая степень нулевого элемента: ij i
o
j i i
0 ij
0 . Здесь R
0 - множество дуг матрицы C
, имеющих нулевое рас min C
min C
, i
, j
j j
0
стояние.
  Затем, среди ij
, i
, j R
0
выбирается дуга i
0
, j
0
1
так, чтобы расстояние Затем, среди ij
, i
, j R
0
выбирается дуга i
0
, j
0
1
так, чтобы расстояние  i
0
j
0
было наибольшим, т.е. i
0 , j
0 1 argmax ij
, i
, j R
0 . i
, j i
0
j
0
было наибольшим, т.е. i
0 , j
0 1 argmax ij
, i
, j R
0 . i
, j
Получив дугу разбиения формируем подмножество дуг, составляющих промежуточные маршруты по ветвям r
1, r
2 шага k
1 : i
0 , j
0 P
11 , P
21 , r
2
P
11 i
0 , j
0 1 , P
11 ,
P
21 , P
21 i
0 , j
0 1
2) Итерация K
1
 А: разбиваем X
0
по i
0
, j
0
1
на 2 подмножества X
i
0
1
j
0
, X
i
0
1
j
0
. А: разбиваем X
0
по i
0
, j
0
1
на 2 подмножества X
i
0
1
j
0
, X
i
0
1
j
0
.
 Подмножество X
i
0
1
j
0
получается из X
0
сужением области за счет введения дополнительных условий: Подмножество X
i
0
1
j
0
получается из X
0
сужением области за счет введения дополнительных условий:
-  запрещается повтор перехода из i
0
в j
0
, переходы из i
0
в j запрещается повтор перехода из i
0
в j
0
, переходы из i
0
в j
 j
0
, переходы из j
0
в i
i
0
, - запрещается обратный переход из j
0
в i
0
. j
0
, переходы из j
0
в i
i
0
, - запрещается обратный переход из j
0
в i
0
.
 Чтобы это формализовать матрица C Чтобы это формализовать матрица C
 C
" преобразуется в матрицу первого шага C
i
0 j
0
следующим образом: C
" преобразуется в матрицу первого шага C
i
0 j
0
следующим образом:
-  в C
строки i
0
и столбец j
0
опускаются, тем самым реализуется первая группа условий; - элемент C
(вторая группа). в C
строки i
0
и столбец j
0
опускаются, тем самым реализуется первая группа условий; - элемент C
(вторая группа).
 Подмножество X
i
0
j
0
получается из X
0
запретом перехода i
0
, j
0
1
, т.е. C
i
0
j
0
: . На каждом подмножестве вычисляется нижняя граница: m
X
i
0
1
j
0
m
0
m
i
0
1
j
0
, m
X
i
0
1
j
0
m
0
i
0
j
0
. Подмножество X
i
0
j
0
получается из X
0
запретом перехода i
0
, j
0
1
, т.е. C
i
0
j
0
: . На каждом подмножестве вычисляется нижняя граница: m
X
i
0
1
j
0
m
0
m
i
0
1
j
0
, m
X
i
0
1
j
0
m
0
i
0
j
0
.
 Примечание. В качестве m
i
0
k
j
0
значения i
0
j
0
значительно сокращается объем вычислений. Примечание. В качестве m
i
0
k
j
0
значения i
0
j
0
значительно сокращается объем вычислений.
Полученная информация о ветвях, границах и множествах заносится на дерево ветвлений.
  Б: по меньшему значению нижней границы находим перспективное для ветвления подмножество. По определению дуги разбиения 1-го шага, им является X
i
0 j
0
, по матрице ему соответствующей приведенной по строкам и столбцам находим дугу разбиения 2-го шага i
0
, j
0
2
. Б: по меньшему значению нижней границы находим перспективное для ветвления подмножество. По определению дуги разбиения 1-го шага, им является X
i
0 j
0
, по матрице ему соответствующей приведенной по строкам и столбцам находим дугу разбиения 2-го шага i
0
, j
0
2
.
 Формируем подмножество дуг, составляющих промежуточные маршруты по ветвям r
1, r
2 . 3) Итерация K Формируем подмножество дуг, составляющих промежуточные маршруты по ветвям r
1, r
2 . 3) Итерация K
 При очередном включении дуги i
0
, j
0
k
в искомый ГК не исключено появление подциклов, т.к. требование замкнутости маршрута отсутствует. При очередном включении дуги i
0
, j
0
k
в искомый ГК не исключено появление подциклов, т.к. требование замкнутости маршрута отсутствует.
 Проанализируем ситуацию, в которой возможно появление подциклов с учетом того, что подцикл i
, i
формализован априори заданием C
ii Проанализируем ситуацию, в которой возможно появление подциклов с учетом того, что подцикл i
, i
формализован априори заданием C
ii
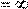 , а подцикл i
0 , а подцикл i
0
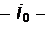 i
0
запрещен правилом формирования мат- i
0
запрещен правилом формирования мат-
рицы C
i
0 j
0 .
   Пусть из элементов P
r
после включения в него i
0
, j
0
( k
)
можно составить маршрут i
0
j
0
u
1
i
0
. Тогда возникает подцикл из u
1
â
i
0
. По соответствующей матрице смотрим, является ли элемент C
ui
0
нулевым. Если не является, то цикла не будет, если является, то цикл возможен и нужно запретить переход u
, i
0
на этот шаг, положив C
ui
0
: Пусть из элементов P
r
после включения в него i
0
, j
0
( k
)
можно составить маршрут i
0
j
0
u
1
i
0
. Тогда возникает подцикл из u
1
â
i
0
. По соответствующей матрице смотрим, является ли элемент C
ui
0
нулевым. Если не является, то цикла не будет, если является, то цикл возможен и нужно запретить переход u
, i
0
на этот шаг, положив C
ui
0
: . .
Аналогично, анализируются другие цепочки маршрутов.
 В вычислительном аспекте бывает проще после того, как было обнаружено появление цикла вернуться на предыдущий шаг к исходному для X
r
подмножеству и соответствующей ему матрицы расстояний и запретить переход, ведущий к образованию данного цикла. В вычислительном аспекте бывает проще после того, как было обнаружено появление цикла вернуться на предыдущий шаг к исходному для X
r
подмножеству и соответствующей ему матрицы расстояний и запретить переход, ведущий к образованию данного цикла.
 Если множесто P
r
состоит ровно из n
1 элемента, то ГК задан однозначно из и нижняя граница на этом подмножестве равна длине единственного цикла минимальной длины. В этом случае ГК является рекордом (претендентом на решение задачи). Если множесто P
r
состоит ровно из n
1 элемента, то ГК задан однозначно из и нижняя граница на этом подмножестве равна длине единственного цикла минимальной длины. В этом случае ГК является рекордом (претендентом на решение задачи).
4) Существуют 3 варианта последовательности разбиения ветвей дерева ветвления:
-  ветвление «полным фронтом», когда на каждом шаге K
вычисляются и сравниваются оценки всех множеств X
rk
, X
rk
, r
1, r
k
; ветвление «полным фронтом», когда на каждом шаге K
вычисляются и сравниваются оценки всех множеств X
rk
, X
rk
, r
1, r
k
;
- ветвление «побегами», при котором разбиение некоторой ветви ведется до момента, когда ее оценка превышает оценку оборванной ветви. Затем развивается оборванная ветвь до момента, когда ее оценка станет хуже;
-   односторонний обход дерева, когда левая ветвь развивается до момента первого рекорда, затем его длина сравнивается с оборванными ветвями и если будет найдена ветвь с наименьшей оценкой, то она развивается до получения 2-го рекорда или до момента, когда m
( X
r
k
) или m
( X
r
k
) станет не лучше текущего значения рекорда. односторонний обход дерева, когда левая ветвь развивается до момента первого рекорда, затем его длина сравнивается с оборванными ветвями и если будет найдена ветвь с наименьшей оценкой, то она развивается до получения 2-го рекорда или до момента, когда m
( X
r
k
) или m
( X
r
k
) станет не лучше текущего значения рекорда.
Меньше всего ветвления дает ветвление полным фронтом и больше всего – односторонний обход, но в вычислительном аспекте он удобен, т.к. количество хранимых незадействованных матриц расстояний здесь меньше. Односторонний обход позволяет применить в качестве первого рекорда приближенное решение задачи о коммивояжере, полученное, например, методом ближайшего соседа.
1.4 МЕТОДЫ ОТСЕЧЕНИЯ. ПЕРВЫЙ АЛГОРИТМ ГОМОРИ
1.4.1 Первый алгоритм Гомори
  Алгоритм Гомори предназначен для решения полностью ЦЗЛП. Алгоритм Гомори реализует пошаговый процесс. Планом на шаге k
0 является решение ЗЛП на допустимой области X
, которая получается из исходной ОДР X
исключением условий целочисленности. Алгоритм Гомори предназначен для решения полностью ЦЗЛП. Алгоритм Гомори реализует пошаговый процесс. Планом на шаге k
0 является решение ЗЛП на допустимой области X
, которая получается из исходной ОДР X
исключением условий целочисленности.
   План на шаге k
1,2,... является решение ЗЛП x k
на области X
, которая строится на основе ОДР предыдущего шага k
1 X k
1
и с учетом дополнительного ограничения l
k
; причем ограничение l
k
вводится не прямо в допустимую область X k
, а опосредованно через введение дополнительной базисной переменной в план предыдущего шага x k
1
. План на шаге k
1,2,... является решение ЗЛП x k
на области X
, которая строится на основе ОДР предыдущего шага k
1 X k
1
и с учетом дополнительного ограничения l
k
; причем ограничение l
k
вводится не прямо в допустимую область X k
, а опосредованно через введение дополнительной базисной переменной в план предыдущего шага x k
1
.
  Пусть получен план шага k
1 и в нем x
j
*
- не целочисленная переменная. По переменной x
j
*
строится так называемое правильное отсечение l
k
таким образом: в базис шага k
1 вводится новая переменная Пусть получен план шага k
1 и в нем x
j
*
- не целочисленная переменная. По переменной x
j
*
строится так называемое правильное отсечение l
k
таким образом: в базис шага k
1 вводится новая переменная
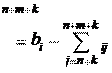 x
. Известно, что любая базисная переменная может быть выражена через свободные по формуле: x
. Известно, что любая базисная переменная может быть выражена через свободные по формуле:
x
á
a x
j
, x
i
*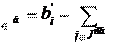 I
a
ij
' x
j
. (1) I
a
ij
' x
j
. (1)
  Здесь b
i
'
- численное значение базисной переменной x
i
á
на шаге k
1 , a
ij
'
- коэффициенты в столбцах замещения при свободных переменных на шаге k
1 , J ñâ
, I á
- множество индексов свободных и базисных переменных. Здесь b
i
'
- численное значение базисной переменной x
i
á
на шаге k
1 , a
ij
'
- коэффициенты в столбцах замещения при свободных переменных на шаге k
1 , J ñâ
, I á
- множество индексов свободных и базисных переменных.
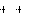 Для вновь вводимой базисной переменной x
n
m k
в правой части соотношения берутся b
i
' Для вновь вводимой базисной переменной x
n
m k
в правой части соотношения берутся b
i
'
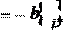 , a
ij
' , a
ij
' 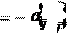 . .
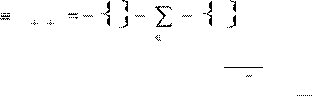 Тогда (1) запишется в виде l
k
x
n m k
b
i
' j
* a
ij
' j
* x
j
. (2) j J
ñâ Тогда (1) запишется в виде l
k
x
n m k
b
i
' j
* a
ij
' j
* x
j
. (2) j J
ñâ
Соотношение (2) задает условие правильного отсечения:
А) условие отсечения – оптимальный план предыдущего шага x
( k
1)
не удовлетворяет (2);
Б) условие правильности – искомый оптимальный план исходной задачи x
*
удовлетворяет (2).
 Можно сказать, что переменная x
n
m k
, введенная в базис таким способом является целой и положительной, т.е. находится в ОДР исходной задачи ЦП. Можно сказать, что переменная x
n
m k
, введенная в базис таким способом является целой и положительной, т.е. находится в ОДР исходной задачи ЦП.
  В тоже время, базис, включающий x
n m k
является недопустимым, т.к. x
n m k
{ b
i
' } j
* 0 . Для нахождения плана на k
-ом шаге следующего шага нужно использовать алгоритм двойственного симплексметода. В тоже время, базис, включающий x
n m k
является недопустимым, т.к. x
n m k
{ b
i
' } j
* 0 . Для нахождения плана на k
-ом шаге следующего шага нужно использовать алгоритм двойственного симплексметода.
В результате применения описанного алгоритма на каждом шаге k
процесса решения задачи от допустимой области предыдущего шага отсекается часть, содержащая нецелочисленный план предыдущего шага. Пошаговая процедура повторяется до получения целочисленного плана исходной задачи или констатации его отсутствия.
Доказательство конечности первого алгоритма Гомори включает в качестве условия требование целочисленности целевой функции и возможность использования строки целевой функции при выборе строки для построения правильного отсечения. Таким образом, для решения задачи методом Гомори следует сделать C j
j
1, n
целыми, это можно сделать, выбрав другие единицы измерения.
 Критерием оптимальности плана является отсутствие отрицательных значений базисных переменных x i
á
0, i I áê
. Здесь I áê
- множество индексов базисных переменных на шаге k
, включая индекс x
n
m k
. Критерием оптимальности плана является отсутствие отрицательных значений базисных переменных x i
á
0, i I áê
. Здесь I áê
- множество индексов базисных переменных на шаге k
, включая индекс x
n
m k
.
1.4.2 Алгоритм двойственного симплекс-метода
Существует двойственный симплекс-метод, или метод последовательного уточнения оценок. Отличие двойственного симплекс-метода от прямого в том, что:
А) двойственный симплекс-метод работает с недопустимым опорным планом;
Б) признаком оптимальности решения является отсутствие в столбце значений базисных переменных отрицательных элементов;
В) выбор разрешающей строки и разрешающего столбца производятся по правилам:

Пересчет элементов таблицы производится так же, как в прямом симплекс-методе.
Примечание 1
. При решении задач, использующих в качестве элемента алгоритма дробную часть числа существенно увеличивается влияние ошибок округления вплоть до возможного получения неправильного решения. Поэтому дробную часть следует брать от числа с обыкновенной дробью. Это условие значительно усложняет программную реализация 1-го алгоритма Гомори.
Примечание 2
. Алгоритм Гомори работает со следующей формой ЗЛП, т.е. задача на максимум и ограничения на равенствах.
1.4.3 Геометрическая интерпретация первого алгоритма Гомори
Для того, чтобы дать геометрическую интерпретацию алгоритма Гомори по шагам нужно произвести переход от представления отсечений через дополнительные переменных канонической системы и переменные отсечений к их представлению через основные переменные.
Это позволяет представить допустимую область k
-го шага как объединение области предыдущего шага и осчечения l
k
:
X
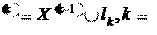 1,2,... . 1,2,... .
Ограничение l
k
получается из правой части выражения для переменной отсечения, вводимой в базис на шаге k
, если выразить входящие в выражения переменные через основные переменные исходной задачи. В результате применения алгоритма Гомори мы переходим от невыпуклой области к выпуклой, причем, искомое решение, являющееся вершиной выпуклой области на предпоследнем шаге лежит на грани и на последнем шаге станет вершиной. Т.е. в общем случае, ограничения-отсечения соединяют точки невыпуклой области, делая ее выпуклой.
Примечание.
Алгоритм отсечения работает только с равенствами и требует целочисленности для всех переменных, поэтому система, в которую вошли дополнительные переменные, должна быть совместна. Когда выбираем переменную, по которой будем строить отсечение желательно, чтобы в базис вводилась переменная из множества переменных основных и дополнительных, а не «бывшая» переменная отсечения.
Двойственный симплекс метод по-другому называется l
-методом. Если в результате решения l
-задачи получается множество оптимальных планов, то метод отсечения применять нельзя.
1.5 ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗЦП
К приближенным методам относят метод ближайшего соседа, метод Фогеля, метод приближенного решения задачи о контейнерных перевозках.
1.5.1 Метод ближайшего соседа
 Применяется для решения задачи о коммивояжере. Последовательно строятся n
путей, в каждом из которых началом берутся i
1,2,... n
, а переход осуществляется по кратчайшему расстоянию между пунктами. Применяется для решения задачи о коммивояжере. Последовательно строятся n
путей, в каждом из которых началом берутся i
1,2,... n
, а переход осуществляется по кратчайшему расстоянию между пунктами.
Затем для каждого пути i
определяется длина пути L
i
и из этих длин выбирается минимальная. ГК, ей соответствующий, является приближенным решением задачи о коммивояжере.
Алгоритм ближайшего соседа употребляется для:
1) поиска приближенного решения, которое может быть использовано для приближенного решения задачи;
2) поиска приближенного решения, которое используется в качестве первого рекорда в алгоритме Литтла.
1.5.2 Задача о контейнерных перевозках
Постановка:
 a j
-вес единицы продукции, j
1, n
; c
j
-ценность единицы продукции, j
1, n
; a j
-вес единицы продукции, j
1, n
; c
j
-ценность единицы продукции, j
1, n
;
b
- допустимый вес (объем, протяженность) контейнера;
x
j
- количество продукции, j
1, n
.
n
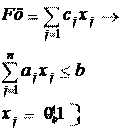 max max
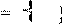 Если задача многомерная, то используются несколько характеристик контейнера: x
j
0, d
j
. Для решения задачи приближенно используется эвристический метод (правдоподобный). Если задача многомерная, то используются несколько характеристик контейнера: x
j
0, d
j
. Для решения задачи приближенно используется эвристический метод (правдоподобный).
1. Предположение:
- включать в контейнер продукцию с большим c
j
;
- включать в контейнер продукцию с малым a
j
.
Схема метода:
- вводится прямоугольная система координат XOY
( AOC
) ;
-   на плоскости строятся точки с координатами a
j
, c
j
, строится луч на плоскости строятся точки с координатами a
j
, c
j
, строится луч 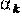 , совпадающий с осью OC
при k
0 ; , совпадающий с осью OC
при k
0 ;
-   этот луч начинают вращать по часовой стрелке, момент перехода луча через l
-тую точку a
l
, c
l
фиксируется как шаг алгоритма kl
; этот луч начинают вращать по часовой стрелке, момент перехода луча через l
-тую точку a
l
, c
l
фиксируется как шаг алгоритма kl
;
- на каждом шаге алгоритма производится назначение x
l
единицей и вычисляется текущее значение левой части ограничения на вместимость контейнера; если ограничение не выполняется, то последнее назначение отменяется и осуществляется переход к следующей точке.
 Процесс продолжается до тех пор, пока лучом не будет пройдена последняя точка из множества j N Процесс продолжается до тех пор, пока лучом не будет пройдена последняя точка из множества j N
(множество точек-продуктов). В результате получим вектор x
, являющийся допустимым в исходной задаче и приближенным решением.
1.5.3 Метод Фогеля для решения задачи о назначении
c
ij
- показатель эффекта от назначения кандидата на место j
;

Данную задачу будем решать на максимум суммарного эффекта. Ее можно решить приближенно за n
шагов так, что на каждом шаге конкретная работа закрепляется за одним кандидатом. Метод является эвристическим. Его положения:
1) выбор работы j
для исполнителя i
или исполнителя i
для работы j
из набора возможных N
, должно производиться по наибольшему значению показателя эффекта c
ij
;
2) назначение i
на j
или j
на i
должно производиться так, чтобы любое другое назначение заметно ухудшало значение функции полезности.
Схема алгоритма:
1)  на каждом шаге k
1,2,... n
для каждого исполнителя i
из N
и работы j
из N
определяется разность между двумя наибольшими элементами на каждом шаге k
1,2,... n
для каждого исполнителя i
из N
и работы j
из N
определяется разность между двумя наибольшими элементами 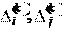 ; ;
2)  из полученных i
k
, k
j
выбирается наибольшее, тем самым определяется направление назначе- из полученных i
k
, k
j
выбирается наибольшее, тем самым определяется направление назначе-
k
ния: если элемент в строке, т.е. i
наибольший, то исполнитель назначается на работу, если элемент в столбце, то работа закрепляется за исполнителем;
3)   А) если максимальный элемент обнаружен в строке i
* , то для исполнителя i
* выбирается работа с наибольшей полезностью, т.е. j
* выбирается так, что c
i
* j
* max , производится назначение i
* на j
* , т.е. x
i
* j
* 1 , i
*, j
* вычеркиваются; А) если максимальный элемент обнаружен в строке i
* , то для исполнителя i
* выбирается работа с наибольшей полезностью, т.е. j
* выбирается так, что c
i
* j
* max , производится назначение i
* на j
* , т.е. x
i
* j
* 1 , i
*, j
* вычеркиваются;
  Б) если максимальный элемент обнаружен в столбце j
* , то ищется исполнитель с наибольшим значением эффекта, т.е. i
* выбирается так, что c
i
* j
* max , производится закрепление j
* за кандидатом на i
* , т.е. x
i
* j
* 1 , i
*, j
* вычеркиваются; Б) если максимальный элемент обнаружен в столбце j
* , то ищется исполнитель с наибольшим значением эффекта, т.е. i
* выбирается так, что c
i
* j
* max , производится закрепление j
* за кандидатом на i
* , т.е. x
i
* j
* 1 , i
*, j
* вычеркиваются;
4) 1-3 повторяются до тех пор, пока не останется 1 элемент, соответствующий последнему назначению.
| I |
J
|
1 |
2 |
… |
N |
 |
| 1 |
| 2 |
| … |
| N |
 |
1.6 ЗАДАЧИ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ С БУЛЕВЫМИ ПЕРЕМЕННЫМИ. АДДИТИВНЫЙ МЕТОД БАЛАША
Рассмотрим задачу с булевыми (бивалентными) переменными:
 (2) . (2) .
(3)
.
  Пробным планом задачи (4)-(7) называется любой ( nm
) -мерный вектор U X
, Y
, удовлетворяющий Пробным планом задачи (4)-(7) называется любой ( nm
) -мерный вектор U X
, Y
, удовлетворяющий
(5)-(6).
Пробный план называется планом, если он удовлетворяет (7) и псевдопланом, если он не удовлетворяет
(7).
План называется оптимальным, если он удовлетворяет (4).
1.6.1 Описание идеи аддитивного алгоритма
Аддитивный алгоритм является методом частичного перебора. Он состоит в получении оптимального плана путем рассмотрения некоторого подмножества всех пробных планов - 2 n
-штук. Это производится в рамках метода ветвей и границ.
 Частичным или q
-планом называется набор, состоящий из q
фиксированных нулем или единицей значений x
j
, j N
, N
- подмножество индексов j
. Частичным или q
-планом называется набор, состоящий из q
фиксированных нулем или единицей значений x
j
, j N
, N
- подмножество индексов j
.
 Дополнением частичного плана называется набор n q
переменных, дополняющий q
-план до плана исходной задачи. Дополнением частичного плана называется набор n q
переменных, дополняющий q
-план до плана исходной задачи.
 Если окажется, что конкретный q
-план имеет дополнения или не имеет дополнения, приводящего к меньшему значению z
, то из рассмотрения можно исключить 2 q
планов и искать оптимальный план среди оставшихся. Если окажется, что конкретный q
-план имеет дополнения или не имеет дополнения, приводящего к меньшему значению z
, то из рассмотрения можно исключить 2 q
планов и искать оптимальный план среди оставшихся.
Анализ (зондирование) q
-плана состоит в:
 А) нахождении наилучшего дополнения, дающего значение Z
меньше, чем полученное ранее; в этом случае определенным образом осуществляется переход к новому q
1 плану; такой план называется расширением q
-плана; А) нахождении наилучшего дополнения, дающего значение Z
меньше, чем полученное ранее; в этом случае определенным образом осуществляется переход к новому q
1 плану; такой план называется расширением q
-плана;
 Б) установлении факта, что таких дополнений нет; в этом случае другие дополнения или расширения q
плана рассматривать не нужно; присвоение последней переменной значения привело в тупик; осуществляется переход к q
1 плану. Б) установлении факта, что таких дополнений нет; в этом случае другие дополнения или расширения q
плана рассматривать не нужно; присвоение последней переменной значения привело в тупик; осуществляется переход к q
1 плану.
1.6.2 Общая схема алгоритма Балаша
В соответствии со схемой ветвей и границ будем считать шагом метода получение допустимого решения – рекорда k
.
В соответствии с алгоритмом Балаша итерацией будем называть включение переменной в q
-план.
Возьмем в качестве начальных условий:
X
0
0, Y
0
B
, Z
0
0, U
0
X
0
, Y
0
0, B
.
 Этот план приносит минимальное значение Z
, т.к. c
j
0 , однако этот план имеет отрицательные ком- Этот план приносит минимальное значение Z
, т.к. c
j
0 , однако этот план имеет отрицательные ком-
 поненты вектора Y
0
, если решение не тривиально. Другими словами, те ограничения (5), для которых y i
0 не выполняются. поненты вектора Y
0
, если решение не тривиально. Другими словами, те ограничения (5), для которых y i
0 не выполняются.
 Переход от пробного плана к плану осуществляется последствием итерации S
1 , причем на каждой итерации S
получается частичное решение в виде: Переход от пробного плана к плану осуществляется последствием итерации S
1 , причем на каждой итерации S
получается частичное решение в виде:
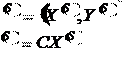 U
(8) U
(8)
Z
(9)
Здесь:
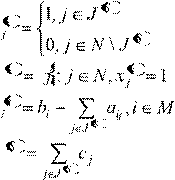 x
(10) x
(10)
J
(11) y
(13)
Z
(14)
Таким образом, алгоритм Балаша должен иметь правила:
1)  формирования подмножеств J S
, N
\ J
; формирования подмножеств J S
, N
\ J
;
2)  перехода от итерации S
к S
1 ; перехода от итерации S
к S
1 ;
3) определения оптимальности решения или неразрешимости исходной задачи.

Булева переменная x
j
называется свободной на S
-ой итерации, если ее значение до S
-ой итерации не зафиксировано ни нулем, ни единицей и подлежит определению в дальнейшем. Введем обозначения:
N
- множество индексов j
свободных на итерации s
переменных;

  M
- множество индексов i
ограничений, для которых дополнительные переменные y
i
0 ; j
- индекс переменной, зафиксированной 1; M
- множество индексов i
ограничений, для которых дополнительные переменные y
i
0 ; j
- индекс переменной, зафиксированной 1;
j
- индекс переменной, зафиксированной 0;
N
' - подмножество индексов переменных, составляющих частичное решение;
N
i
- множество индексов свободных переменных в ограничении i
, которые могут быть включены в частичное решение;
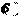
J
- индексы переменных, для которых было сделано назначение единицей.
1.6.3 Правила построения частичного решения
Правило 1
.Правило по которому из числа свободных исключаются переменные, усиливающие недопустимости для данной итерации s
или шага k
.
  Если на итерации s
переменная x
r
, r N
s
i M i
: y
i
0 : a
ir
0 , то присвоение x
r
: 1 Если на итерации s
переменная x
r
, r N
s
i M i
: y
i
0 : a
ir
0 , то присвоение x
r
: 1
усиливает недопустимости во всех строках i M
. В этом случае на итерацию S
переменная x r
, r
 S
исключается. S
исключается.
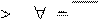 В случае, когда a
ir
0 i
1, m
переменная x
r
исключатся насовсем. В случае, когда a
ir
0 i
1, m
переменная x
r
исключатся насовсем.
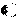 Правило 2
. Запрет недопустимых вариантов ветвления, когда дополнение частичного решения не может быть получено, т.е. отрицательность y
i
не может быть устранена. Правило 2
. Запрет недопустимых вариантов ветвления, когда дополнение частичного решения не может быть получено, т.е. отрицательность y
i
не может быть устранена.
Если на S
хотя бы для одного i
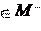 не выполняется неравенство не выполняется неравенство 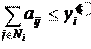 , где , где
 N i
j
: j N
', a
ij
0 , то данный вариант ветвления отбрасывается и осуществляется переход к N i
j
: j N
', a
ij
0 , то данный вариант ветвления отбрасывается и осуществляется переход к
( q
1) плану или другому частичному решению.
Если неравенство выполняется, то данный вариант ветвления должен быть развит.
Правило 3
. Запрет неперспективных в смысле улучшения рекорда направления ветвления на итерации S
и для шага K
.
  Если был получен рекорд rec
и значение целевой функции предыдущего шага z s
1
известно, то для переменной x
l
, l Если был получен рекорд rec
и значение целевой функции предыдущего шага z s
1
известно, то для переменной x
l
, l
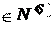 и при этом c
l и при этом c
l
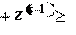 rec
, то присвоение переменной x
l
: 1 на итерации S
не rec
, то присвоение переменной x
l
: 1 на итерации S
не
улучшит z
в сравнении с рекордом, т.е. x
l
не перспективно и развитие варианта по x
l
следует прекратить.
 Если коэффициент при x
l
c
l
сам не меньше рекорда c
l
rec
, то x
l
не может быть зафиксирован единицей до конца процесса решения задачи. Если коэффициент при x
l
c
l
сам не меньше рекорда c
l
rec
, то x
l
не может быть зафиксирован единицей до конца процесса решения задачи.
  Правила 1,2,3 формируют на основе N s
1
набор свободных переменных, которые могут быть зафиксированы на итерации S
, т.е. N
. Правила 1,2,3 формируют на основе N s
1
набор свободных переменных, которые могут быть зафиксированы на итерации S
, т.е. N
.
Правило 4
. Выбор направление ветвления.
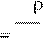 Для выбора направления ветвления используется оценка j
, которая есть сумма недопустимостей по пе- Для выбора направления ветвления используется оценка j
, которая есть сумма недопустимостей по пе-
 ременной j
во всех ограничениях i
1, m
, которая возникнет, если x
j
: 1 : ременной j
во всех ограничениях i
1, m
, которая возникнет, если x
j
: 1 :
m
min 0, y S
1
a
j
i ij
. i
1
  Из всех j
, j N S
выбирается та, которая приносит меньше суммарной недопустимости, т.е. учитывая, то j
0 выбирается максимальное: j
* arg max
S
j
. j N Из всех j
, j N S
выбирается та, которая приносит меньше суммарной недопустимости, т.е. учитывая, то j
0 выбирается максимальное: j
* arg max
S
j
. j N
1.6.4 Алгоритм метода Балаша
 . .
     Записываем: новый рекорд rec
min rec
, rec
k Записываем: новый рекорд rec
min rec
, rec
k
 для s
1 ; rec
min( rec
k
1 , rec
k
) , записываем X N
', Y
. Идем на дерево ветвлений. для s
1 ; rec
min( rec
k
1 , rec
k
) , записываем X N
', Y
. Идем на дерево ветвлений.
В) если недопустимости есть, т.е. M
 , а свободных переменных нет N , а свободных переменных нет N
 , то ветвь тупиковая и исключается из просмотра. , то ветвь тупиковая и исключается из просмотра.
3) Для i
 проверяем правило 1. проверяем правило 1.
При необходимости корректируем N
; если перспективных вариантов нет, то возвращаемся назад и пересчитываем условия.
4)  для i для i
 образуем N
i
j
: j N
', a
ij
0 и проверяем правило 2. образуем N
i
j
: j N
', a
ij
0 и проверяем правило 2.
5) Если ранее был получен рекорд, то проверяем правило 3.

Получили набор свободных переменных N
.
6)  по правилу 4 для j N S
выбираем x
j
*
; по правилу 4 для j N S
выбираем x
j
*
;
 Расчитываем для ветвей x
j
* 1, x
j
* 0 показатели: А) x j
*
1 : Расчитываем для ветвей x
j
* 1, x
j
* 0 показатели: А) x j
*
1 :
N
 N
' N
'
J
.
y
z j
 Б) x Б) x
N
N
'
J
. y
z
j
1.6.5 Сведение ЗЦП в общей постановке к задаче с булевыми переменными
Пусть все условия, необходитмые для метода Балаша выполняются, т.е. задача на минимум, ограничения типа 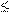 , коэффициенты функции цели неотрицательны, но переменные, все или часть, могут принимать целочисленные значения. Тогда эти переменные можно перевести в булевы, используя следующий прием: 1) пусть известна верхняя граница изменения x
j
- d
j
. , коэффициенты функции цели неотрицательны, но переменные, все или часть, могут принимать целочисленные значения. Тогда эти переменные можно перевести в булевы, используя следующий прием: 1) пусть известна верхняя граница изменения x
j
- d
j
.
2)  Для каждой d
j
можно определить k
j
, при котором выполняется условие: d
j
2 k
2 k
1 ... 2 0 2 k
1 1 . Для каждой d
j
можно определить k
j
, при котором выполняется условие: d
j
2 k
2 k
1 ... 2 0 2 k
1 1 .
3)  Далее, зная k
j
каждую переменную x
j
можно представить в виде двоичного разложения: x
j
2 k
t
k
1 2 k
1 t
k
2 0 t
1 , t
k
0,1 . Далее, зная k
j
каждую переменную x
j
можно представить в виде двоичного разложения: x
j
2 k
t
k
1 2 k
1 t
k
2 0 t
1 , t
k
0,1 .
4)  Получив такие двоичные разложения для каждого x
j
Z
подставим их в ЗЦП и получим задачи с бивалентными переменными, решаем ее методом Балаша и по двоичному разложению восстанавливаем x
j
. Получив такие двоичные разложения для каждого x
j
Z
подставим их в ЗЦП и получим задачи с бивалентными переменными, решаем ее методом Балаша и по двоичному разложению восстанавливаем x
j
.
 Если коэффициенты c
j
0 , то t
j Если коэффициенты c
j
0 , то t
j

1.7 ПРИБЛИЖЕННОЕ РЕШЕНИЕ. ИСПОЛЬЗОВАНИЕ ТОЧНЫХ МЕТОДОВ И ТОЧНОРЕШАЕМЫХ ЗАДАЧ
Задача целочисленного программирования:
 Z
max (1) Z
max (1)
x
(2)
 D
-допустимое конечное или счетное множество планов, которое задается ограничениями на x x
1
, x
2
,..., x n D
-допустимое конечное или счетное множество планов, которое задается ограничениями на x x
1
, x
2
,..., x n
 . .
Если для x
условия принадлежности области D
выполняются, то решение допустимое x
' ; если для x
' достигается экстремум целевой функции, то решение оптимальное x
* .
Любое допустимое решение можно считать приближенным с некоторой точностью.
 1.7.1 Оценка качества приближенного решения Абсолютная погрешность решения x
' равна: z
( x
') (3). 1.7.1 Оценка качества приближенного решения Абсолютная погрешность решения x
' равна: z
( x
') (3).
Относительная погрешность: (4).
Если погрешности равны 0, то приближенное решение является точным. Если абсолютная погрешность не равна нулю, то (3) и (4) служат для оценки качества или точности приближения. n
Запишем функцию цели в виде: f
( x
)  c
x
j
(5) c
x
j
(5)
При этом если c
j
одного знака, то использование (3) и (4) являются оправданными. Если c
j
разных зна-

В этом случае f
( x
) может оказаться малой разностью больших величин.
   Пусть в качестве f
( x
) используется доход, f
1
( x
) - прибыль, f
2
( x
) - затраты, причем равны соответственно 1001 и 1000 (в оптимальном плане). Тогда f
( x
*) 1 . Требуется оценить приближение f x
' 0 через относительную погрешность: 1 . Пусть в качестве f
( x
) используется доход, f
1
( x
) - прибыль, f
2
( x
) - затраты, причем равны соответственно 1001 и 1000 (в оптимальном плане). Тогда f
( x
*) 1 . Требуется оценить приближение f x
' 0 через относительную погрешность: 1 .
Такая погрешность будет всегда для разности близких величин. И такое положение, не зависящее от слагаемых величин, не допустимо, следовательно, использование (4) здесь не уместно. Для такого случая за f
( x
*) f
( x
')
 пишем относительную погрешность: ' (6). f
1
( x
*) f
2
( x
*) пишем относительную погрешность: ' (6). f
1
( x
*) f
2
( x
*)
На этом примере видно, что в каждом конкретном случае оценка решения производится исходя из содержательной постановки задачи и тесно связана с ней.
Все ЗЦП можно разделить на 2 класса:
1) задачи, для которых легко найти допустимые решения, а значит решить приближенно; поиск точного решения задач может быть очень трудным;
2) Задачи, для которых трудно найти допустимое решение, поиск приближенного решения сопоставим по трудностям с нахождением точного решения.
К задачам 1-го класса относятся эвристические алгоритмы поиска приближенного решения.
Задачи 2-го класса используют для получения приближенного решения следующие методы:
1) аппроксимация на основе точных методов и точно решаемых задач;
2) методы локальной оптимизации;
3) случайного поиска;
4) случайного поиска с локальной оптимизацией; 5) методы, использующие специфику задачи.
 Рассмотрим использование точных методов для построения приближенного решения. Предположим, что задача решается некоторым точным методом и в процессе решения строится последовательность допустимых решений x
0
, x
1
,..., x
k
, упорядоченная по значению целевой функции: f
( x
0
) f
( x
1
) ... f
( x k
) Рассмотрим использование точных методов для построения приближенного решения. Предположим, что задача решается некоторым точным методом и в процессе решения строится последовательность допустимых решений x
0
, x
1
,..., x
k
, упорядоченная по значению целевой функции: f
( x
0
) f
( x
1
) ... f
( x k
)  f
( x
*) (7) f
( x
*) (7)
Если последовательность допустимых решения слишком длинная, то ее можно прервать на любом шаге l
и принять x
l
за приближенное решение.
Например, метод Лэнда и Дойга на каждой большой итерации строит допустимый целочисленный план – рекорд. Если рекорды упорядочить по (7), то прервав последовательность рекордов на любом шаге, получим решение приближенное соответствующей точности.
Метод отсечения Гомори не порождает приближенных решений, т.к. первое допустимое решение является точным решением задачи.
Все методы ветвей и границ порождают приближенное решение.

Пусть f
( x
*) - рекорд, z
- верхняя граница целевой функции.
  Тогда точное решение будет в интервале f
( x
k
) f
( x
*) z
. Тогда точное решение будет в интервале f
( x
k
) f
( x
*) z
.
Таким образом, методы ветвей и границ порождают не только приближенное решение, но и дают оценку их отклонения от оптимума (если известно z
).
1.7.2 Использование точно решаемых задач для получения приближенного решения
В рамках метода ветвей и границ используется прием релаксации ограничений. Применительно к ЗЦП он состоит в отбрасывании условия целочисленности и в переходе к задаче ЛП.
Задача ЛП решается точно, и если исходная задача на максимум, то получается соответствие: f
( x
')  f
( x ö
) f
( x ö
)  f
( x ÇËÏ
) . f
( x ÇËÏ
) .
Аналогичным образом, задача о назначении может быть использована при релаксации задачи коммивояжера путем отбрасывания условия запрещения подциклов.
32
|