Реферат: Спектральный анализ и синтез сигнала

Министерство образования Республики Беларусь

Учреждение образования

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра радиотехнических устройств

К защите допустить:

Руководитель проекта

______В.М.Дашенков

Пояснительная записка

к курсовому проекту

на тему:

« Спектральный анализ и синтез сигнала »

Выполнил: Руководитель проекта:

Студент ФРЭ гр.741301 Дашенков В.М.

Домасевич В.Л.

Минск 2009

Содержание

1. Введение и постановка задачи

Теория радиотехнических цепей и сигналов является фундаментальной дисциплиной, которая своим содержанием определяет профессиональную подготовку инженеров.

Влияние этой научной теории огромно и в настоящее время, и дальнейшее развитие теории очень важно для современного общества, и будет происходить в обозримом будущем. Это объясняется тем, что потребность в качественной передаче и обработке непрерывно растущих объемов информации постоянно нарастает. При этом основная проблема, заключающаяся в отыскании методов передачи и приема, обеспечивающих получение требуемой достоверности принимаемых сообщений и повышение скорости передачи, все еще остается актуальной.

2. Спектральные свойства сигнала

Сигнал и событие

Событие (получение записки, наблюдение сигнальной ракеты, прием символа по телеграфу) является сигналом только в той системе отношений, в которой сообщение опознается значимым (например, в условиях боевых действий сигнальная ракета — событие, значимое только для того наблюдателя, которому оно адресовано). Очевидно, что сигнал, заданный аналитически, событием не является и не несет информацию, если функция сигнала и её параметры известны наблюдателю.

В технике сигнал всегда является событием. Другими словами, событие - изменение состояния любого компонента технической системы, опознаваемое логикой системы как значимое, является сигналом. Событие, неопознаваемое данной системой логических или технических отношений как значимое, сигналом не является.

Временной и частотный способ представления сигналов. Спектр сигнала.

Есть два способа представления сигнала в зависимости от области определения: временной и частотный. В первом случае сигнал представляется функцией времени s(t) характеризующей изменение его параметра.

Кроме привычного временного представления сигналов и функций при анализе и обработке данных широко используется описание сигналов функциями частоты. Действительно, любой сколь угодно сложный по своей форме сигнал можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, совокупность которых называется частотным спектром сигнала.

Для перехода к частотному способу представления используется преобразование Фурье:

S(ω)=.

Функция S(ω) называется спектральной функцией или спектральной плотностью.

Поскольку спектральная функция S(ω) является комплексной, то можно говорить о спектре амплитуд | S(ω) | и спектре фаз φ(ω) = arg(S(ω)). Физический смысл спектральной функции: сигнал s(t) представляется в виде суммы бесконечного ряда гармонических составляющих (синусоид) с амплитудами , непрерывно заполняющими интервал частот от 0 до , и начальными фазами φ(ω). Размерность спектральной функции есть размерность сигнала, умноженная на время.

Параметры сигналов

Мощность сигнала P = .

Удельная энергия сигнала E .

Длительность сигнала (T) определяет интервал времени, в течение которого сигнал существует (отличен от нуля).

Динамический диапазон есть отношение наибольшей мгновенной мощности сигнала к наименьшей D = 10lgPmax / Pmin.

Ширина спектра сигнала F — полоса частот, в пределах которой сосредоточена основная энергия сигнала[~95%].

База сигнала есть произведение длительности сигнала на ширину его спектра B = TF. Необходимо отметить, что между шириной спектра и длительностью сигнала существует обратно пропорциональная зависимость: тем короче спектр, тем больше длительность сигнала. Таким образом, величина базы остается практически неизменной.

Отношение сигнал/шум равно отношению мощности полезного сигнала к мощности шума.

Объем сигнала характеризует пропускную способность канала связи, необходимую для передачи сигнала. Он определяется как произведение ширины спектра сигнала на его длительность и динамический диапазон

V = FTD.

Итак, среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов для радиотехники обусловлено рядом причин.

В радиотехнике приходится иметь дело с электрическими сигналами, которые связаны с передаваемыми сообщениями принятым способом кодирования.

Можно сказать, что электрический сигнал представляет собой физический (электрический) процесс, несущий в себе информацию. Количество информации, которое можно передать с помощью некоторого сигнала, зависит от основных его параметров: длительности, полосы частот, мощности и некоторых других характеристик. Важное значение имеет также уровень помех в канале связи: чем меньше этот уровень, тем большее количество информации можно передать с помощью сигнала с заданной мощностью. Прежде чем говорить об информационных возможностях сигнала, необходимо ознакомиться с его основными характеристиками. Целесообразно рассмотреть отдельно детерминированные и случайные сигналы.

Детерминированным называют любой сигнал, мгновенное значение которого в любой момент времени можно предсказать с вероятностью равной единице.

Примерами детерминированных сигналов могут служить импульсы или пачки импульсов, форма, величина и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра. Детерминированные сигналы можно подразделить на периодические и непериодические.

Периодическим называется любой сигнал, для которого выполняется условие s ( t )= s ( t + k Т), где период Т является конечным отрезком, а k – любое целое число.

Простейшим периодическим детерминированным сигналом является гармоническое колебание. Строго гармоническое колебание называют монохроматическим. Этот заимствованный из оптики термин подчёркивает, что спектр гармонического колебания состоит из одной спектральной линии. У реальных сигналов, имеющих начало и конец, спектр неизбежно размывается. Поэтому строго монохроматического колебания в природе не существует. В дальнейшем под гармоническим и монохроматическим сигналом условно будет подразумеваться колебание. Любой сложный периодический сигнал, как известно, можно представить в виде суммы гармонических колебаний с частотами, кратными основной частоте w = 2* Pi / T . Основной характеристикой сложного периодического сигнала является его спектральная функция, содержащая информацию об амплитудах и фазах отдельных гармоник.

Непериодическим детерминированным сигналом называется любой детерминированный сигнал, для которого выполняется условие s ( t ) s ( t + kT ).

Как правило, непериодический сигнал ограничен во времени. Примерами таких сигналов могут служить уже упоминавшиеся импульсы, пачки импульсов, «обрывки» гармонических колебаний и т.д. Непериодические сигналы представляют основной интерес, так как именно они преимущественно используются в практике.

Основной характеристикой непериодического, как и периодического сигнала, является его спектральная функция.

К случайным сигналам относят сигналы, значения которых заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Такими функциями являются, например, электрическое напряжение, соответствующее речи, музыке, последовательности знаков телеграфного кода при передаче неповторяющегося текста. К случайным сигналам относится также последовательность радиоимпульсов на входе радиолокационного приёмника, когда амплитуды импульсов и фазы их высокочастотного заполнения флуктуируют из-за изменения условий распространения, положения цели и некоторых других причин. Можно привести большое число других примеров случайных сигналов. По существу, любой сигнал, несущий в себе информацию, должен рассматриваться как случайный. Перечисленные детерминированные сигналы, «полностью известные», информация уже не содержат. В дальнейшем такие сигналы часто будут обозначаться термином «колебание».

Для характеристики и анализа случайных сигналов применяется статистический подход. В качестве основных характеристик случайных сигналов принимают:

а) закон распределения вероятностей.

б) спектральное распределение мощности сигнала.

На основе первой характеристики можно найти относительное время пребывания величины сигнала в определённом интервале уровней, отношение максимальных значений к среднеквадратическому и ряд других важных параметров сигнала. Вторая характеристика даёт лишь распределение по частотам средней мощности сигнала. Более подробной информации относительно отдельных составляющих спектра – об их амплитудах и фазах – спектральная характеристика случайного процесса не даёт.

Наряду с полезными случайными сигналами в теории и практике приходится иметь дело со случайными помехами – шумами. Как уже упоминалось выше, уровень шумов является основным фактором, ограничивающим скорость передачи информации при заданном сигнале.

2.1 Спектральные характеристики периодических сигналов

Для упрощения методов решения задач анализа цепей, сигналы представляют в виде суммы определенных функций.

Этот процесс обосновывается понятием обобщенного ряда Фурье. В математике доказано, что любая функция, удовлетворяющая условиям Дирихле, может быть представлена в виде ряда:

.

Для определения умножим левую и правую части ряда на и возьмем интеграл от левой и правой части:

, для интервала [a;b] в котором выполняются условия ортогональности.

Видно, что .Получили выражение для обобщенного ряда Фурье:

.

Выделим конкретный вид функции , для разложения в ряд сигнала . В качестве такой функции выберем ортогональную систему функций:

Для определения ряда вычислим значение :

.

, так как .

Таким образом, получим:

, где

.

Графически данный ряд представляется в виде двух графиков амплитудных гармонических составляющих.

Полученное выражение можно представить в виде:

где ; .

Получили вторую форму записи тригонометрического ряда Фурье. Графически данный ряд представляется в виде двух графиков - амплитудного и фазового спектров.

Найдем комплексную форму ряда Фурье, для этого воспользуемся формулами Эйлера:

или , где

Графически спектр в этой форме представлен на оси частот в диапазоне .

Очевидно, что спектр периодического сигнала, выраженный в комплексной или амплитудной форме – дискретный. Это значит, что в спектре имеются составляющие с частотами

2.2 Спектральные характеристики непериодического сигнала

Так как в качестве непериодического сигнала в радиотехнике рассматривают одиночный сигнал, то для нахождения его спектра представим сигнал как периодический с периодом . Воспользуемся преобразование ряда Фурье для данного периода. Получим для :

.

Анализ полученного выражения показывает, что при амплитуды составляющих становятся бесконечно малыми и на оси частот они расположены непрерывно. Тогда, что б выйти из этого положения воспользуемся понятием спектральной плотности:

.

Подставим полученное выражение в комплексный ряд Фурье, получим:

.

Окончательно получим:

.

Здесь - спектральная плотность, а само выражение – прямое преобразование Фурье. Для определения сигнала по его спектру используют обратное преобразование Фурье:

.

Свойства преобразования Фурье

Из формул прямого и обратного преобразований Фурье, очевидно, что если изменится сигнал, то изменится и его спектр. Следующие свойства устанавливают зависимость спектра измененного сигнала, от спектра сигнала до изменений.

1) Свойство линейности преобразования Фурье:

.

, т.е.

.

Получили, что спектр суммы сигналов равен сумме их спектров.

2) Спектр сигнала сдвинутого во времени:

.

.

.

Получили, что при сдвиге сигнала амплитудный спектр не изменяется, а изменяется только фазовый спектр на величину

3) Изменение масштаба времени:

.

т.е при расширении(сужении) сигнала в несколько раз спектр этого сигнала сужается(расширяется).

4) Спектр смещения:

.

.

5) Спектр производной от сигнала:

.

Возьмем производную от левой и правой части обратного преобразования Фурье:

.

.

Видим, что спектр производной от сигнала равен спектру исходного сигнала умноженного на , то есть изменяется амплитудный спектр и меняется фазовый на

6) Спектр интеграла сигнала:

.

Возьмем интеграл от левой и правой части обратного преобразования Фурье:

.

.

Видим, что спектр производной от сигнала равен спектру исходного сигнала деленного на .

7) Спектр произведения двух сигналов:

.

.

.

Таким образом, спектр произведения двух сигналов равен свертке их спектров умноженной на коэффициент .

8) Свойство дуальности:

.

.

Таким образом, если к какому-то сигналу соответствует спектр , то сигналу по форме совпадающему с вышеуказанным спектром соответствует спектр по форме совпадающий с вышеуказанным сигналом.

9) Теорема о свёрке 2-х функций:

.

.

.

Синтез сигнала в полосе частот (0,50кГц )

Рис. 8

Синтез сигнала в полосе частот (0,75кГц )

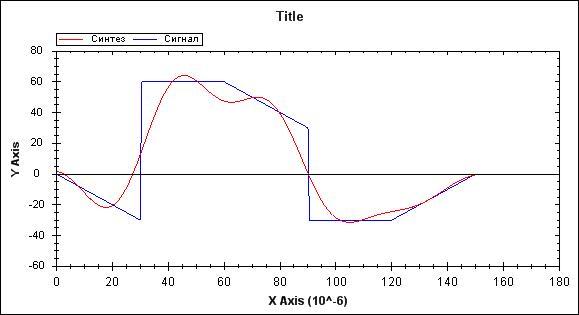
Рис. 9

Синтез сигнала в полосе частот (0,100кГц )

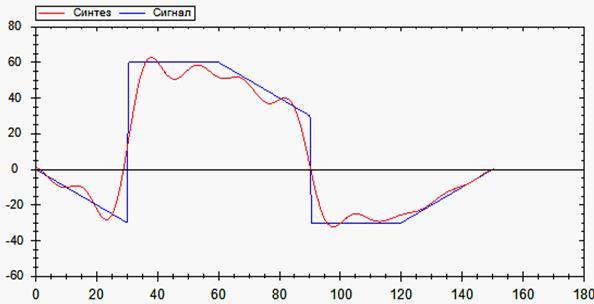
Рис. 10

Приложение 3

При выполнении данной работы была написана программа на языке C Sharp.

Внешний вид:

Рис. 11

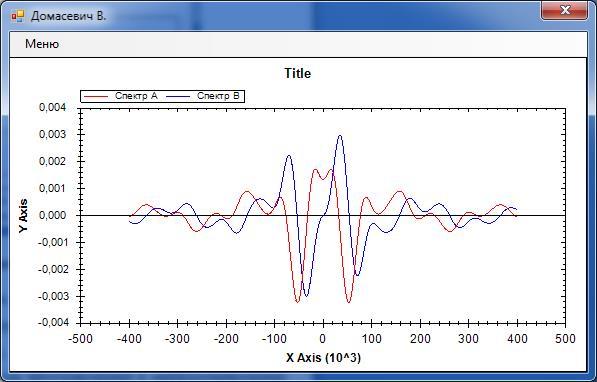
Рис. 12

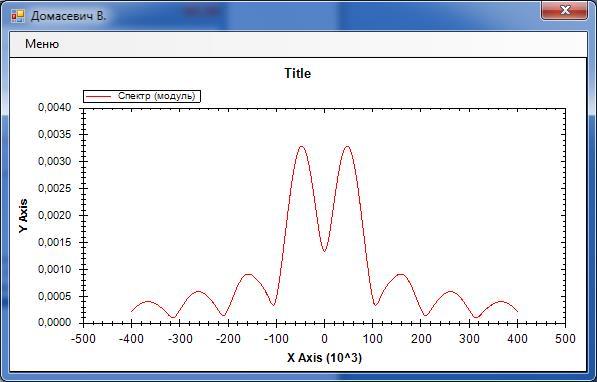
Рис. 13

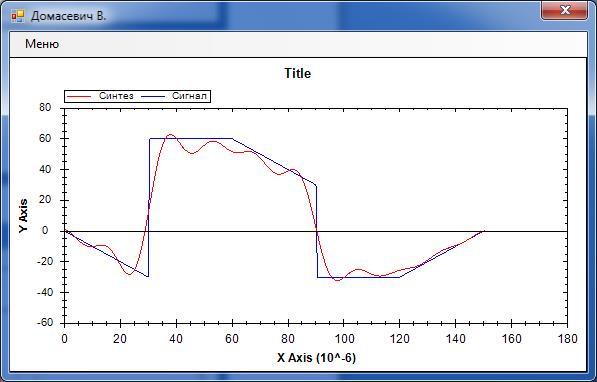
Рис. 14

Рис. 15

Заключение

В ходе выполнения данной работы, на конкретном примере, был произведен расчет спектра сигнала. C помощью прямого преобразования Фурье на каждом из интервалов функции исходного сигнала. Неоценимую помощь оказали свойства преобразования Фурье, а особенно свойства интегрирования и дифференцирования. Благодаря этим свойствам расчёт спектра выходного сигнала стал значительно легче.

Основной трудностью при выполнении курсового проекта являлся расчёт синтеза сигнала на основании его спектра, что было связано с громоздкостью аналитического выражения для спектра выходного сигнала, и следовательно, с трудностью расчёта его интеграла. Обычными методами интеграл рассчитать не удалось. Поэтому для этой цели была написана программа на языке программирования C Sharp. В которой для расчета интеграла был использован один из численных методов, а именно метод с автоматическим выбором шага по заданной точности, достоинствами которого является простота реализации, высокая точность и надёжность выполнения кода.

В ходе выполнения курсовой работы, были использованы некоторые программные приложения: MS Office 2007, MathCAD 14 и графическое приложение MS Pain. Расчет и построение некоторых графиков производились при помощи программного пакета MathCAD 14, оформление и редактирование отчёта о проделанной работе выполнялось при помощи приложений MS Office 2007 и графического редактора Paint.

Список использованной литературы