| Федеральное агентство по образованию
Саратовский Государственный университет им. Н. Г. Чернышевского
Химический факультет
Кафедра общей и неорганической химии
Туннельный эффект
(холодная эмиссия электронов и контактная разность потенциалов)
КУРСОВАЯ РАБОТА
Студента 1 курса химического факультета
Снесарева Сергея Владимировича
Научный руководитель
доктор химических наук, профессор
С. П. Муштакова
Заведующий кафедрой
доктор химических наук, профессор
С. П. Муштакова
Саратов
2006
Содержание
Введение
§1. Прямоугольный потенциальный барьер.
§2. Кажущаяся парадоксальность «туннельного эффекта».
§3. Вырывание электронов из металла. Холодная эмиссия.
§4. Контактная разность потенциалов
Заключение
Список литературы
Введение
 Туннельный эффект (туннелирование) — квантовый переход системы через область движения, запрещённую классической механикой. Типичный пример такого процесса— прохождение частицы через потенциальный барьер,
когда её полная энергия Е
меньше высоты барьера (рис 1.1). Туннельный эффект (туннелирование) — квантовый переход системы через область движения, запрещённую классической механикой. Типичный пример такого процесса— прохождение частицы через потенциальный барьер,
когда её полная энергия Е
меньше высоты барьера (рис 1.1).
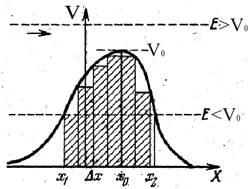
рис 1.1 Потенциальный барьер в одном измерении
Согласно классической теории частица может находиться только в тех точках пространства, в которых потенциальная энергия V меньше её полной энергии E. Это следует из того обстоятельства, что кинетическая энергия частицы
(1.1)
всегда должна быть положительной величиной. В области V>E - потенциальный барьер
- импульс имеет мнимое значение и присутствие там частицы в рамках классической теории является совершенно недопустимым.
Поэтому, если две области пространства, для которых E>V, отделены друг от друга потенциальным барьером, внутри которого V>E, то по классической теории просачивание частицы из одной области в другую через потенциальный барьер невозможно. По волновой же теории мнимое значение импульса соответствует лишь экспоненциальной зависимости волновой функции от координаты. Поскольку волновая функция внутри потенциального барьера в нуль не обращается, то вполне возможно и просачивание частицы сквозь потенциальный барьер. Для микрочастиц это явление может стать даже вполне наблюдаемым.
Туннельный эффект является специфическим лишь для волновой теории и не имеет какого-либо аналога в классической механике.

рис 1.2 Прохождение частицы сквозь потенциальный барьер
§1. Случай прямоугольного барьера
Определим прежде всего вероятность прохождения микрочастицы через потенциальный барьер прямоугольной формы (рис. 1.2) в предположении, что энергия частицы Е меньше высоты потенциального барьера V0
. Допустим, что частица движется в положительном направлении оси x. Волны де Бройля, соответствующие движению частицы, частично отразятся от барьера, а частично пройдут сквозь него и будут распространяться в области x>a (рис 1.2). В этой задаче мы должны найти прежде всего волновые функции, а затем на границах потенциального барьера “сшить” их, т.е. приравнять как сами волновые функции, так и их производные.
Решение уравнения Шредингера для каждой из 3-х областей имеет вид:
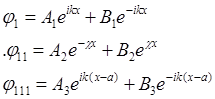 
Здесь
(волновой вектор).
A
1
eikx
и B
1
e
-
ikx
характеризуют соответственно падающую и отраженную волны, A
3
eik
(
x
-
a
)
- прошедшую, а B
3
e
-
ik
(
x
-
a
)
– волну, идущую из бесконечности в направлении противоположном падающей волны.
Поскольку последняя в нашем случае отсутствует, необходимо положить B
3
=0
. Для характеристики величины туннельного эффекта введем коэффициент прозрачности барьера, под которым будем понимать модуль отношения плотности потока частиц, прошедших через барьер, к плотности потока падающих частиц:
(1.3)
Для определения потока частиц воспользуемся формулой:
(1.4)
Подставляя в эту формулу решение уравнения Шредингера (1.2) для коэффициента прозрачности D, находим:
(1.5)
Для определения коэффициента прохождения воспользуемся граничными условиями при x
=
a
и x
=0
и выразим сначала А2
и В2
через А3
, учитывая, что χa>>1,
(1.6)
а затем А1
через А3
:

Тогда для коэффициента прохождения (диффузии) D получаем выражение:
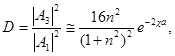 (1.8) (1.8)
Где 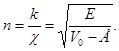
Вводя величину 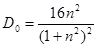 , получаем: , получаем:
 (1.9) (1.9)
где D0
порядка единицы.
рис 1.3 схема барьера произвольной, но достаточно гладкой формы
Если мы хотим обобщить формулу (1.9) на потенциальный барьер произвольной формы (рис 1.3), то соответствующую задачу лучше всего решать методом ВКБ.
При этом мы должны произвести замену

где координаты x1
(начало барьера) и x2
(конец барьера) находятся из условия
V(x1
)=V(x2
)=E.
Тогда для коэффициента прохождения D через барьер произвольной формы получается выражение:
 (1.8) (1.8)
Движение частиц внутри потенциального барьера представляет собой типичное проявление волновых свойств микрочастиц, Поэтому оно должно в той или иной степени проявляться в любой волновой теории. В частности, в оптике этим аналогом может служить хорошо известное явление полного внутреннего отражения (рис 1.5), которое может наблюдаться в случае отражения света при сравнительно больших углах от оптически менее плотной среды.



§ 2. Кажущаяся парадоксальность «туннельного эффекта»
Прохождение частиц через потенциальные барьеры представляется на первый взгляд парадоксальным. Эту парадоксальность усматривают в том, что частица, находящаяся внутри потенциального барьера при полной энергии Е,
меньшей высоты барьера V
0
,
должна иметь отрицательную кинетическую энергию 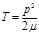 ,
и полная энергия, как это имеет место в классической механике, является суммой энергий кинетической и потенциальной: ,
и полная энергия, как это имеет место в классической механике, является суммой энергий кинетической и потенциальной:

В области, где, V
>Е,
 это бессмысленно, так как импульс это бессмысленно, так как импульс 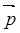 есть действительная величина. Как раз эти области, как мы знаем из классической механики, недоступны для частицы. Между тем, согласно квантовой механике, частица может быть обнаружена и в этой «запретной» области. Таким образом, получается, будто квантовая механика приводит к выводу, что кинетическая энергия частицы может быть отрицательной, а импульс частицы мнимым. Этот вывод и называют парадоксом «туннельного эффекта». есть действительная величина. Как раз эти области, как мы знаем из классической механики, недоступны для частицы. Между тем, согласно квантовой механике, частица может быть обнаружена и в этой «запретной» области. Таким образом, получается, будто квантовая механика приводит к выводу, что кинетическая энергия частицы может быть отрицательной, а импульс частицы мнимым. Этот вывод и называют парадоксом «туннельного эффекта».
На самом деле здесь нет никакого парадокса, а сам вывод неверен. Дело в том, что, поскольку туннельный эффект есть явление квантовое (при ħ → 0 коэффициент прозрачности D (1.8) стремится к нулю), постольку он может обсуждаться лишь в рамках квантовой механики. Полную же энергию частицы можно рассматривать как сумму кинетической и потенциальной энергий только на основе классической механики. Формула 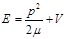 предполагает, что одновременно знаем величину как кинетической энергии Т, так и потенциальной
V
.
Иными словами, мы приписываем одновременно определенное значение координате частицы х
и ее импульсу р, что противоречит квантовой механике. Деление полной энергии на потенциальную и кинетическую в квантовой механике лишено смысла, а вместе с тем несостоятелен и парадокс, основанный на возможности представить полную энергию Е
как сумму кинетической энергии (функция импульса) и потенциальной энергии (функция координат). предполагает, что одновременно знаем величину как кинетической энергии Т, так и потенциальной
V
.
Иными словами, мы приписываем одновременно определенное значение координате частицы х
и ее импульсу р, что противоречит квантовой механике. Деление полной энергии на потенциальную и кинетическую в квантовой механике лишено смысла, а вместе с тем несостоятелен и парадокс, основанный на возможности представить полную энергию Е
как сумму кинетической энергии (функция импульса) и потенциальной энергии (функция координат).
Остается лишь посмотреть, не может ли все же оказаться так, что путем измерения положения частицы мы обнаружим ее внутри потенциального барьера, в то время как ее полная энергия меньше высоты барьера.
Обнаружить частицу внутри барьера действительно можно, даже если E
<
V
;
однако если фиксируется координата частицы х,
при этом создается, согласно соотношению неопределенности, дополнительная дисперсия в импульсе  так что уже нельзя утверждать, что энергия частицы, после того как определили ее положение, равна Е. так что уже нельзя утверждать, что энергия частицы, после того как определили ее положение, равна Е.
Из формулы для коэффициента прозрачности следует, что частицы проникают заметным образом лишь на глубину. Чтобы обнаружить частицу внутри барьера, мы должны фиксировать ее координату с точностью ∆x < l. Но тогда неизбежно возникает дисперсия импульса:
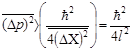
Подставляя сюда l
2
, находим
 (2.1)
(2.1)
т. е. изменение кинетической энергии частицы, вносимое вмешательством измерения, должно быть больше той энергии, которой ей недостает до высоты барьера V
0
.
Приведем еще пример, иллюстрирующий это утверждение. Определить координату частицы, находящейся внутри потенциального барьера таким путем, что будем посылать - узкий пучок света в направлении, перпендикулярном к направлению движения частицы. Если пучок рассеется, то значит, на его пути попалась частица.
Как объяснялось выше, точность нашего измерения должна быть такова ∆X<l; с другой стороны, нельзя создать пучок света, ширина которого была бы меньше длины световой волны λ, а, следовательно, длина волны света должна быть меньше l, т. е.
 (2.2) (2.2)
так как  , где ω - частота световых колебаний, а с - скорость света, то отсюда следует, что , где ω - частота световых колебаний, а с - скорость света, то отсюда следует, что

Встречающиеся в нерелятивистской механике энергии должны быть меньше собственной, энергии частицы mс2
, поэтому
 (2.3) (2.3)
т. е. энергия применяемых в световом пучке квантов света должна быть больше, нежели разность между высотой потенциального барьера и энергией частицы. Таким образом, этот пример иллюстрирует положение о необходимости применить для измерения координаты приборы, обладающие достаточно большой энергией, чтобы можно было локализовать частицу.
§ 3.
Вырывание электронов из металла. Холодная эмиссия
Теория туннельного эффекта имеет ряд весьма важных приложений в теории металлов и в ядерной физике. С помощью этой теории удалось понять ряд явлений, которые не нашли своего объяснения в классической физике. К числу этих явлений следует в первую очередь отнести холодную эмиссию, т. е. вырывание электронов из металла под действием электрического поля, а также возникновение контактной разности потенциалов. Однако прежде всего скажем несколько слов о теории «электронного газа», лежащей в основе электронной теории проводимости металлов.
Высокая электропроводность металлов говорит о том, что электроны способны сравнительно свободно перемещаться внутри всей кристаллической решетки металла. Затруднен лишь их выход из металла в вакуум, требующий затраты некоторой энергии, так называемой работы выхода. Это наводит на мысль рассматривать простейшую модель металла как свободный электронный газ, движущийся в потенциальной яме, внутри которой (т. е. в металле) потенциальная энергия равна нулю V=0, а вне, т. е. в вакууме, V=Vо
>0.
Подобная упрощенная модель позволяет уяснить многие явления в металлах и поэтому в некоторых пределах является вполне разумной. Она была введена еще в классической теории (теория Друде, Лоренца и т. д.). В этом случае к электронам применялась классическая статистика Максвелла—Больцмана, которая до этого с успехом объяснила многие явления кинетической теории газов.
Однако в классической теории модель «электронного газа» встретила большие затруднения при построении теории теплоемкости. В самом деле, согласно известной теореме классической статистической механики о равномерном распределении энергии по степеням свободы на одну степень свободы в среднем должна приходиться энергия:
 (3.1) (3.1)
Отсюда видно, что доля каждого свободного электрона в общей теплоемкости такая же, как и свободного атома
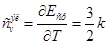
Это противоречит экспериментальным фактам, согласно которым теплоемкость одноатомного металла определяется лишь теплоемкостью атомов решетки, т. е. свободные электроны в первом приближении никакого вклада в теплоемкость металла не вносят.
Это противоречие было разрешено Зоммерфельдом, который показал, что к электронам в металле необходимо применять не классическую статистику с функцией распределения

а квантовую статистику Ферми – Дирака с функцией распределения

В основе квантовой статистики Ферми—Дирака лежит принцип Паули, согласно которому на каждом энергетическом уровне может находиться максимум два электрона (два квантовых состояния, отличающихся направлениями спинов).
Если нам задана трехмерная потенциальная яма кубической формы с длиной стороны, равной L, то составляющие импульса p
=ђk
будут связаны с целыми числами n1
, n2
, nз
, характеризующими энергетический уровень, соотношениями:

Учтем, что на единичный интервал квантовых чисел:
 (3.2) (3.2)
приходится лишь один уровень, на котором могут находиться два электрона.
Поэтому если в единице объема находится ρо
электронов, то максимальный импульс, которым может обладать электрон при абсолютном нуле температуры (T=0), определяется из соотношения
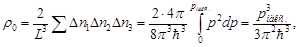 (3.3) (3.3)
Или 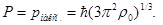 (3.4) (3.4)
Соответствующая максимальная кинетическая энергия электронов равна:
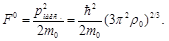 (3.5) (3.5)
Эта максимальная энергия при T= 0 соответствует уровню Ферми. Оценим значение этой энергии, например, для серебра. Плотность серебра равна 10,5, атомный вес 107,9. Считая, что число свободных электронов равно числу атомов серебра в единице объема, имеем:

Здесь мы использовали число Авогадро, т. е. число атомов в одном грамм-атоме, равное 6,02·1023
. Отсюда по формуле (3.5) находим, что

    Поскольку для серебра работа выхода W=3,7 эВ, то глубина потенциальной ямы в серебре оказывается равной 9,8 эВ. Схема заполнения электронных уровней в металле изображена на рис 3.1. Поскольку для серебра работа выхода W=3,7 эВ, то глубина потенциальной ямы в серебре оказывается равной 9,8 эВ. Схема заполнения электронных уровней в металле изображена на рис 3.1.
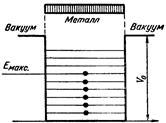
рис 3.1 Модель потенциальной ямы для металла. (Е макс. – верхняя граница заполненных уровней при Т=0 (энергия Ферми).
Средняя энергия в металле будет определяться выражением
 (3.6) (3.6)
Отсюда видно, что при сравнительно низких температурах электронный газ никакого вклада в теплоемкость не должен вносить, так как

Исходя из этой модели (рис 3.1), мы видим, что для вырывания электрона из металла необходимо сообщить ему энергию не меньшую, чем работа выхода
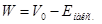 (3.7) (3.7)
Как известно, в случае внешнего фотоэффекта электрон получает от поглощенного фотона энергию ђω. При этом электрон может покинуть металл, обладая кинетической энергией.
 (3.8) (3.8)
(уравнение Эйнштейна). Отсюда следует, что работа выхода есть минимальная энергия, которую нужно затратить, чтобы энергия электрона стала больше высоты потенциального барьера.
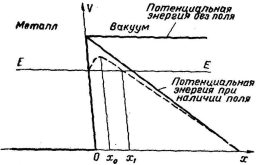
рис 3.2 Потенциальная энергия электрона в металле без поля и при наличии внешнего электрического поля. (штриховой линией показан ход потенциальной кривой с учетом сил электростатического изображения)
Если электроны в металле (электронный газ) имеют температуру выше абсолютного нуля, то часть электронов заполняет энергетические уровни выше уровня Ферми. Если увеличить кинетическую энергию электронного газа путем нагревания металла, то некоторая часть электронов может иметь энергию, превышающую энергию потенциального барьера, благодаря чему возникает ток из металла. Это явление, получившее название термоэлектронной эмиссии, используется, в частности для получения пучка электронов в электронных лампах. Однако возникновение тока электронов возможно и при низких температурах под влиянием постоянного внешнего электрического поля напряженности ξ
, приложенного к поверхности проводника и направленного против оси –х. В этом случае потенциальная энергия электрона заряда -е0
равна (рис 3.2):
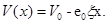 (3.9) (3.9)
Помимо внешнего электрического поля, на электрон действует так называемая сила электрического изображения. Дело в том, что электрон, обладая зарядом —e
о
,
создает на поверхности металла индуцированный заряд e
о
(рис 3.3).
Таким образом, полная сила, действующая на электрон, равна
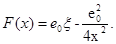 (3.10) (3.10)
Эффективная потенциальная энергия, учитывающая силы электрического изображения, равна:
 (3.11) (3.11)
Величина Vэфф
имеет максимум в точке x0
:
 (3.12) (3.12)

причем максимальное значение Vэфф
меньше У0
, так как
 (3.13) (3.13)
Учет сил электрического изображения показывает, что при наложении внешнего поля работа выхода уменьшается и становится равной
 (3.14) (3.14)
Однако силы электрического изображения не в состоянии объяснить холодную эмиссию. Действительно, оценка максимального тока (при W=0) приводит, например, для вольфрама к значению
 (3.15) (3.15)
между тем как на опыте достаточно сильный ток появляется уже при поле Е@4·106
в/см (Малликен).

рис 3.3 Силы электрического изображения: на находящийся вне металла электрон действуют силы притяжения индуцированным зарядом.
Таким образом, в рамках классической теории невозможно объяснить с количественной стороны явление холодной эмиссии.
В квантовой теории, когда допустимо прохождение электронов сквозь потенциальный барьер, для потенциальной энергии можно ограничиться выражением (3.9) и не учитывать сил электрического изображения, поскольку последние лишь весьма незначительно изменят окончательный результат. Из графика потенциальной энергии (рис 3.2) видно, что внешнее электрическое поле создает потенциальный барьер конечной ширины. Благодаря туннельному эффекту электрон может преодолеть этот барьер, причем коэффициент прозрачности равен
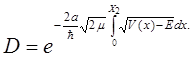 (3.16) (3.16)
Интеграл в экспоненте должен быть взят по всей ширине барьера от точки х=0 до точки х=х1
, которая определяется из условия
 (3.17) (3.17)
Тогда
 (3.18) (3.18)
Окончательно для коэффициента прозрачности D получаем выражение:
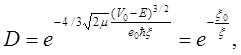 (3.19) (3.19)
где величина ξ0
зависит от работы выхода из металла свободных электронов. Ток холодной эмиссии пропорционален коэффициенту прозрачности
 (3.20) (3.20)
Отсюда следует, что холодная эмиссия должна наблюдаться при напряженности электрического поля ξ~106
в/см, что хорошо согласуется с экспериментальными данными.
§ 4. Контактная разность потенциалов
На основе туннельного эффекта можно объяснить и явление так называемой контактной разности потенциалов, которое было открыто ещё Вольтом.
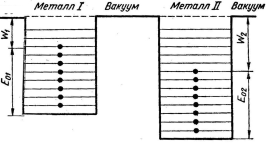
рис 4.1 Два металла до сближения: W1
и W2
– работа выхода; E01
b E02
– верхние границы заполненных уровней (энергия Ферми)
Рассмотрим два металла различной природы, обладающих различными работами выхода, а вместе с тем и уровнями Ферми (рис 4.1). Если привести их в соприкосновение, то они оказываются разделенными потенциальным барьером конечной ширины. Поскольку часть занятых электронами энергетических уровней в металле I лежит выше границы заполненных уровней металла II, возможен туннельный переход электронов на свободные уровни металлов II. Обратный переход, как видно из 6.6, исключен, поскольку электроны металла II при таком переходе будут иметь энергию, соответствующую заполненным уровням металла I. Очевидно, далее, что возникший электрический ток прекратится только в том случае, когда верхнее заполненные уровни металлов сравняются.
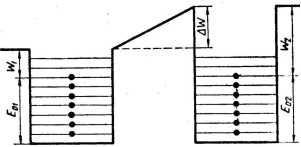
рис 4.2 Два металла после сближения. Возникновение контактной разности потенциалов.
В результате туннельного эффекта металл II, получив избыток электронов, заряжается отрицательно и соответственно металл I заряжается положительно. При этом начало отсчета энергетических уровней металла II поднимается вверх по отношению к началу отсчета уровней металла I (рис 4.2). После того как наступило термодинамическое равновесие, при котором уровни Ферми в обоих металлах должны сравняться, электрический ток прекратится, но зато между металлами возникает разность потенциалов, пропорциональная разности работ выхода:
 (4.1) (4.1)
Эта величина и представляет собой контактную разность потенциалов.
Заключение
Туннельный эффект обусловливает возможность протекания термоядерных реакций на Солнце и звёздах при температуре в десятки и сотни млн. градусов,
а также в земных условиях в виде термоядерных взрывов.
В симметричном потенциале, состоящем из двух одинаковых ям, разделённых слабопроницаемым барьером, туннельный эффект приводит к интерференции состояний в ямах, что приводит к слабому двойному расщеплению дискретных уровней энергии.
Для бесконечного периодичного в пространстве набора ям каждый уровень превращается в зону энергий. Таков механизм образования узких электронных энергетических зон в кристаллах с сильной связью электронов с узлами решётки.
Если к полупроводниковому кристаллу приложено электрическое поле, то зоны разрешённых энергий электронов становятся наклонными в пространстве. Тем самым уровень потенциальной энергии электрона пересекает все зоны. В этих условиях становится возможным переход электрона из одной энергетической зоны в другую за счёт туннельного эффекта. Классически недоступной областью при этом является зона запрещённых энергий. Это явление называется пробоем Зинера. Квазиклассическое приближение отвечает здесь малой величине напряжённости электрического поля. В этом пределе вероятность пробоя Зинера определяется в основном экспонентой, в показателе которой стоит большая отрицательная величина, пропорциональная отношению ширины запрещённой энергетической зоны к энергии, набираемой электроном в приложенном поле на расстоянии, равном размеру элементарной ячейки.
Похожий эффект проявляется в туннельных диодах,
в которых зоны наклонены благодаря полупроводникам р-
и n
-
типа по обе стороны от границы их соприкосновения. Туннелирование осуществляется благодаря тому, что в зоне, куда переходит носитель заряда, имеется конечная плотность незанятых состояний.
Благодаря туннельному эффекту возможен электрический ток между двумя металлами, разделёнными тонкой диэлектрической перегородкой. Эти металлы могут находиться как в нормальном, так и в сверхпроводящем состоянии. В последнем случае может иметь место Джозефсона эффект.
Туннельному эффекту обязаны такие явления, происходящие в сильных электрических полях, как автоионизация атомов и автоэлектронная эмиссия
из металлов. В обоих случаях электрическое поле образует барьер конечной прозрачности. Чем сильнее электрическое поле, тем прозрачнее барьер и тем сильнее электронный ток из металла. На этом принципе основан сканирующий туннельный микроскоп
- прибор, измеряющий туннельный ток из разных точек исследуемой поверхности и дающий информацию о характере её неоднородности. Используя туннельный ток как индикатор приближения к поверхности и нарисовав несколько вариантов её профилей, можно сложить из рисунков трехмерную картинку исследуемой поверхности. Сканирующий микроскоп, удерживая постоянную величину туннельного тока, рисует ту поверхность, на которой вероятность пребывания электронов постоянна, то есть, по сути, ту самую пси-функцию, которую используют для описания квантовых объектов.
Туннельный эффект возможен не только в квантовых системах, состоящих из одной частицы. Так, например, низкотемпературное движение дислокаций в кристаллах может быть связано с туннелированием конечной части дислокации, состоя из многих частиц. В такого рода задачах линейную дислокацию можно представить как упругую струну, лежащую первоначально вдоль оси у
в одном из локальных минимумов потенциала V
(
x
, у).
Этот потенциал не зависит от у,
а его рельеф вдоль оси х
представляет собой последовательность локальных минимумов, каждый из которых находится ниже другого на величину, зависящую от приложенного к кристаллу механического напряжения. Движение дислокации под действием этого напряжения сводится к туннелированию в соседний минимум определенного отрезка дислокации с последующим подтягиванием туда оставшейся её части. Такого же рода туннельный механизм может отвечать за движение волн зарядовой плотности
в диэлектрике Пайерлса.
Для расчётов эффектов туннелирования таких многоразмерных квантовых систем удобно использовать квазиклассическое представление волновой функции в виде ψ~exp(iS), S
—классическое действие системы. Для туннельного эффекта существенна мнимая часть S
,
определяющая затухание волновой функции в классически недоступной области. Для её вычисления используется метод комплексных траекторий.
Квантовая частица, преодолевающая потенциальный барьер может быть связана с термостатом. В классической механике это соответствует движению с трением. Тем самым, для описания туннелирования необходимо привлечение теории, получившей название диссипативной квантовой механики. Такого рода соображения необходимо использовать для объяснения конечного времени жизни токовых состояний контактов Джозефсона. В этом случае происходит туннелирование эффекта квантовой частицы через барьер, а роль термостата играют нормальные электроны.
Список литературы
1. Д. И. Блохинцев “Основы квантовой механики”. – М.: Наука, 1976.
2. А. А. Соколов, И. М. Тернов “Квантовая механика и атомная физика”. Учебн. пособие для физ.-мат. фак-тов пединститутов. М.: Просвещение, 423 с. с илл., 1970.
3. П. Эткинс “Кванты справочник концепций”. – М.: Мир, 496 с., 1977.
4. Гоголинский К. “Орбитали зондовой микроскопии”/ К. Гоголинский, В. Решетов// Вокруг Света, М.: Вокруг света.- 2005. - №6. – с. 106-114.
|