| ТРЕХМЕРНОЕ НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ СИСТЕМЫ РОЛИК-ВАЛ В УСЛОВИЯХ КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ И НЕКОНТАКТНОГО ИЗГИБА ВАЛА
A.Б. Иванов1)
, В.Г. Петров 1)2)*
1)
Механико-математический факультет, Белорусский государственный университет
2)
Межведомственная лаборатория “ТРИБОФАТИКА”
*
Автор, с которым следует вести переписку.
| Реферат
Система ролик/вал представляет собой характерную силовую систему и является моделью таких практически важных объектов как зубчатое зацепление, колесо-рельс, вал-подшипник качения и др. Область контакта вала и ролика является наиболее нагруженной в рассматриваемой системе. В данной области трехмерное напряженно-деформированное состояние обусловлено независимыми граничными условиями как при контакте, так и при изгибе.
Трехмерное напряженное состояние силовой системы ролик/вал определяется как суперпозиция полей напряжений, вызванных соответственно нормальной контактной, касательной контактной и неконтактной нагрузками.
Приведенные результаты численных расчетов показали, что изгиб вала существенно изменяет (качественно и количественно) напряженно-деформированное состояние в окрестности контакта, а, следовательно, несущую способность и эксплуатационную долговечность системы.
|
|
1. Введение
Одним из основных направлений исследований в трибофатике является построение механико-математических моделей напряженно-деформированного состояния силовых систем. Силовыми являются механические системы, в которых одновременно реализуется контактное взаимодействие с трением (качения, скольжения) между твердыми деформируемыми телами и неконтактное (объемное) деформирование по крайней мере одного из элементов силовой системы [1-3].
Изучение трехмерного напряженно-деформированного состояние механических систем, одновременно работающих в условиях контактного взаимодействия и объемного (неконтактного) деформирования, является необходимым для корректной оценки надежности и долговечности таких систем
Система ролик-вал представляет собой характерную силовую систему и является моделью таких практически важных объектов как зубчатое зацепление, колесо-рельс, вал-подшипник качения и др. Область контакта вала и ролика является наиболее нагруженной в рассматриваемой системе. В данной области трехмерное напряженно-деформированное состояние обусловлено независимыми граничными условиями как при контакте, так и при изгибе.
2. Напряженное состояние
Силовая система ролик-вал нагружена контактной FN
a и неконтактной Q
нагрузками (рис. 1).
Тогда напряженное состояние силовой системы диск-цилиндр определяется как суперпозиция полей
напряжений 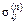 , , 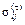 и и 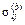 , вызванных соответственно нормальной контактной, касательной контактной и неконтактной нагрузками [1,2]: , вызванных соответственно нормальной контактной, касательной контактной и неконтактной нагрузками [1,2]:
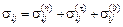 , i
, j
= x
, y
, (1) , i
, j
= x
, y
, (1)
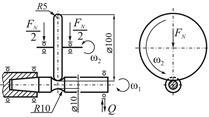
Рис. 1. Схема нагружения системы ролик-вал
Расчет напряжений 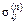 и и 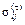 в любой точке полупространства ( в любой точке полупространства (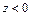 ) при действии на поверхность нормальных p
(x
,y
) и касательных fp
(x
,y
) контактных усилий проводится численно с использованием функций влияния ) при действии на поверхность нормальных p
(x
,y
) и касательных fp
(x
,y
) контактных усилий проводится численно с использованием функций влияния 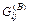 и и 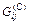 из решений задач Буссинеска и Черрути о действии сосредоточенных нормальной и касательной сил на полупространство [1,2]: из решений задач Буссинеска и Черрути о действии сосредоточенных нормальной и касательной сил на полупространство [1,2]:
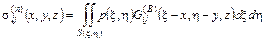 (2) (2)
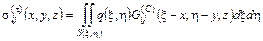 (3) (3)
Напряжения от неконтактных нагрузок будем определять, применяя теорию, подходящую для конкретной геометрии и граничных условий взаимодействующих тел [1,2]:
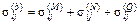 (4) (4)
где индексы M
, N
и Q
соответствуют внутренним моменту, продольному и поперечному усилиям.
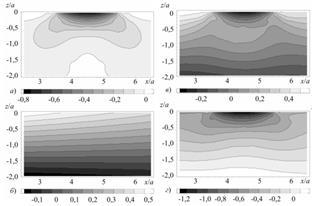
Рис. 1. Распределение напряжений 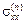 (а
), (а
), 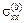 (б
), (б
), 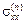 + +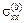 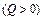 (в
), (в
),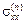 – –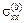 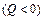 (г
), отнесенных к максимальному (г
), отнесенных к максимальному 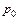 , в окрестности площадки контакта (y
= 0, а /
b
= 0,5) , в окрестности площадки контакта (y
= 0, а /
b
= 0,5)
3. Заключение
Из полученных распределений напряжений, представленных на рис 1, хорошо видно, что напряженно-деформированное состояние силовой системы значительно отличается (качественно и количественно) от таковых при традиционно отдельно изучаемых контакте и изгибе.
Таким образом, с одной стороны, можно исследовать как поле напряжений, обусловленных объемным деформированием, возмущается в локальной области, в которой одновременно возбуждается поле контактных напряжений. Такой анализ полезен, когда в силовой системе реализуется прямой эффект [1] С другой стороны, можно интересоваться, как изменяется локальное поле контактных напряжений, когда на него накладывается поле напряжений, обусловленных объемным деформированием. Такой анализ полезен, когда в силовой системе реализуется обратный эффект [1].
Литература
[1] Сосновский, Л.А. “Механика износоусталостного повреждения,” БелГУТ, 2007, 434 с.
[2] Журавков, М.А., Щербаков С.С., “Исследование сопряженного напряженного состояния в условиях контактного нагружения и объемного деформирования,” Вести НАНБ. Сер. 1., 3, 2008, 60–64.
[3] Журавков, М.А., Щербаков С.С., “Исследование опасных объемов при решении контактной задачи для системы ролик / кольцо,” Тр. V Междунар. симпозиума по трибофатике (ISTF 2005), Иркутск, 2005, Т. 1., 375–390.
Об авторах
| 
|
Иванов Андрей Борисович,
доктор физ.-мат. наук, профессор, профессор кафедры теоретической и прикладной механики БГУ,
Научные интересы:
Методы аналитического и компьютерного
|
| моделирования в механике деформируемого твердого тела
Автор
более 150 научных работ; в том числе 2-х монографий, и одного учебного пособия.
e-mail
: ivanov@bsu.by
|
| 
|
Петров Валерий Георгиевич,
кандидат техн. наук, доцент,
доцент кафедры теоретической и прикладной механики БГУ, ведущий научный сотрудник Межведомственной лаборатории
|
| «ТРИБОФАТИКА»
Научные интересы:
методологические, теоретические и экспериментальные основы трибофатики.
Автор
более 80 научных работ.
e-mail
: petrov@bsu.by
|
Three-dimensional stress-strain state
of
roller-shaft system in conditions of contact interaction and non-contact bending of shaft
| Abstract
Roller/shaft system is a typical active system that is a model of such practically important systems as toothings, wheel/rail, shaft/rolling bearing etc. Area of contact between shaft and roller is the most loaded region in the considered system. Three-dimensional stress-strain state in this area is caused by independent boundary conditions for both contact and non-contact bending of the shaft.
General three-dimensional stress state of the roller/shaft active system was obtained by superposing the fields of stresses conditioned both by action of normal and tangential elliptically distributed contact loads and by non-contact bending of the shaft.
The results of numerical calculations are presented. They show that non-contact shaft’s bending essentially changes (qualitatively and quantitatively) stress-strain state in contact neighborhood and hence operational durability of system is changed significantly.
|
|
|