| Министерство образования Российской Федерации
Ивановский государственный университет
Кафедра общей физики
Вольт-амперная характеристика
протяженного металлического проводника
Методические указания
к учебно-исследовательской работе (УИРС)
для студентов 2 курса
физического факультета
Иваново
Издательство “Ивановский государственный университет”
2001
Составители: кандидат физико-математических наук А.П. Блинов
,
кандидат педагогических наук В.Е. Кулаков
,
кандидат физико-математических наук В.В. Смирнов
Методические указания содержат постановку и анализ задачи о вольт-амперной характеристике металлического проводника и алгоритм ее численного решения с возможным использованием средств компьютерной техники.
Для студентов 2 курса физического факультета.
Печатается по решению методической комиссии физического факультета Ивановского государственного университета
Рецензент:
кандидат физико-математических наук Е.А. Ноговицын (ИвГУ)
Составители:
БЛИНОВ Анатолий Павлович
КУЛАКОВ Владимир Евгеньевич
СМИРНОВ Владимир Владимирович
Вольт-амперная характеристика протяженного металлического проводника
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К УЧЕБНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЕ (УИРС)
для студентов 2 курса физического факультета
Редактор В.А.Киселева
Лицензия ЛР № 020295 от 22.11.96. Подписано в печать 4.02.2001.
Формат 60 х 84 1/16
Бумага писчая. Печать Плоская. Усл.печ.л.0,70.
Уч .-изд. л. 0,6. Тираж 50 экз.
Ивановский государственный университет
Печатно-множительный участок ИвГУ
153025, Иваново, ул.Ермака, 39
ã Ивановский государственный университет, 2001
Введение
Настоящие методические указания предназначены для студентов 2 курса физического факультета ИвГУ, изучающих раздел курса общей физики «Электричество и магнетизм».
Новый государственный стандарт физического образования предполагает глубокое усвоение основных физических понятий и законов. Этому способствует активное применение полученных знаний в процессе решения стандартных задач на семинарских занятиях. Указанные задачи, несомненно, способствуют закреплению изученного материала, формируют умения и навыки его практического применения.
Отметим, что самостоятельное решение указанных задач делает данную работу наиболее эффективной.
Вместе с тем целесообразно в учебный процесс вводить задачи, носящие научно-исследовательский характер (УИРС). Указанные задачи способствуют формированию умений и навыков, необходимых будущему физику-исследователю. Эти задачи более сложные и, как правило, носят комплексный характер. Такие задачи целесообразно предъявлять студентам для самостоятельной работы с возможностью консультаций с преподавателем в процессе их решения.
Решенные задачи могут обсуждаться на семинарских и лабораторных занятиях. Это способствует формированию у студентов умений и навыков выступать с краткими докладами, по форме приближенными к докладам на научных конференциях.
Одним из возможных направлений указанной деятельности является постановка и решение задач по электричеству и магнетизму. В настоящих методических указаниях в качестве образца приводится пример постановки и решения задачи о нахождении вольт-амперной характеристики протяженного металлического проводника с учетом выделения джоулева тепла и зависимости удельного электрического сопротивления от температуры. Рассматривается модель комплекса перечисленных явлений, носящая нетривиальный характер. Решение указанной задачи позволяет на практике воспользоваться тем математическим инструментарием, которым к моменту ее решения располагают студенты (обыкновенные дифференциальные уравнения), и познакомиться с ситуацией, когда становится ясной необходимость его расширения (интегро-дифференциальные уравнения).
Кроме того в методических указаниях приводится пример алгоритма численного решения задачи с возможным использованием средств компьютерной техники, что также необходимо будущему исследователю.
Вольт-амперная характеристика протяженного металлического проводника
Прохождение электрического тока по проводнику описывается вольт-амперной характеристикой, т.е. зависимостью между силой тока I в проводнике и разностью потенциалов ( напряжением ) U между двумя фиксированными точками ( сечениями ) этого проводника:
I = f(U) . (1)
В общем случае зависимость (1) между I и U нелинейна, однако на практике всегда можно в определённом интервале напряжений считать её линейной и применять закон Ома:
I = U/rп
, (2)
где rп
– сопротивление соответствующего участка проводника, находящегося под напряжением U.
В дифференциальной форме закон Ома выражает линейную зависимость плотности электрического тока 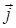 от напряжённости электрического поля от напряжённости электрического поля 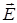 в данной точке проводника [3]: в данной точке проводника [3]:
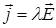 , (3) , (3)
где 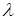 - удельная проводимость ( электропроводность ) материала проводника. Величина, обратная электропроводности, называется удельным сопротивлением материала: - удельная проводимость ( электропроводность ) материала проводника. Величина, обратная электропроводности, называется удельным сопротивлением материала:
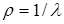 . (4) . (4)
Удельное сопротивление 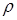 зависит от температуры T проводника, причём для металлов при обычных температурах зависит от температуры T проводника, причём для металлов при обычных температурах 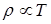 . .
Строго говоря, закон Ома (2) справедлив лишь для физически однородных тел. Последнее означает, что переход от дифференциальной формы (3) к интегральной (2) закона Ома и обратно возможен, если температура протяжённого проводника, в частности, постоянна по всему его объёму. Однако последнее обстоятельство является идеализацией. Вследствие выделения джоулева тепла при прохождении электрического тока по проводнику последний должен разогреваться. Если проводник окружён теплонепроницаемой (адиабатической) оболочкой, температура в каждой его точке будет расти со временем t . При постоянном отводе тепла через граничную поверхность протяжённого проводника возникает стационарное, т.е. не зависящее от времени, распределение температуры по объёму проводника. В этом случае проводник будет характеризоваться в каждой точке своим значением удельного сопротивления (4), зависящего от температуры. В итоге проводник перестанет быть физически однородным, а интегральная линейная зависимость (2) между током I и напряжением U не будет иметь места. При этом следует отметить то обстоятельство, что в данном случае речь не идёт о нарушении закона Ома в дифференциальной форме (3) , что может происходить в сильных полях, когда на протяжении среднего свободного пробега носитель тока приобретает скорость, сравнимую с тепловой. Так, при прохождении электрического через металл нелинейные эффекты могли бы проявиться начиная с полей 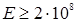 В/м. Однако такие поля в металлах невозможны, так как мгновенно превратили бы металл в пар. Реально же поля существенно меньше приведённой выше величины. Например, для меди технически допустимые поля меньше этой величины в 109
раз. С этим обстоятельством и связана практически неограниченная применимость закона Ома (3) к металлам. В/м. Однако такие поля в металлах невозможны, так как мгновенно превратили бы металл в пар. Реально же поля существенно меньше приведённой выше величины. Например, для меди технически допустимые поля меньше этой величины в 109
раз. С этим обстоятельством и связана практически неограниченная применимость закона Ома (3) к металлам.
Рассмотрим проводник из чистого металла цилиндрической формы длиной l и радиуса R.
Пусть l >> R и температура боковой поверхности проводника поддерживается постоянной и равной T0
. При прохождении электрического тока по проводнику джоулево тепло, удельная мощность которого равна 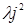 , отводится в окружающее пространство за счёт механизма теплопроводности. Пусть далее W – объёмная плотность внутренней энергии в металле и , отводится в окружающее пространство за счёт механизма теплопроводности. Пусть далее W – объёмная плотность внутренней энергии в металле и 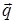 - плотность теплового потока . Тогда уравнение теплового баланса имеет вид - плотность теплового потока . Тогда уравнение теплового баланса имеет вид
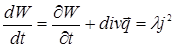 . (5) . (5)
В (5) 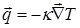 и и  , где , где 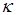 - коэффициент теплопроводности и - коэффициент теплопроводности и 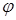 - потенциал электрического поля в металле. - потенциал электрического поля в металле.
В стационарном случае, когда 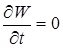 , получим , получим
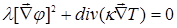 . (6) . (6)
Кроме того,
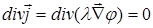 . (7) . (7)
Равенство (7) выражает закон сохранения носителей тока (в данном случае – электронов).
Для чистых металлов, согласно закону Видемана-Франца, при температурах T, больших температуры Дебая, [2]
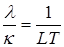 , (8) , (8)
где L= 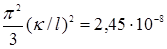 Вт Ом / град2
– число Лоренца, причём Вт Ом / град2
– число Лоренца, причём 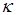 не зависит от температуры. не зависит от температуры.
Перейдём в (6) и (7) к цилиндрическим координатам ( 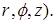 Для бесконечно длинного провода ( l>> R ) из изотропного чистого металла температура T в стационарном случае будет зависеть только от радиальной переменной r ( 0 £ r £ R ) : Для бесконечно длинного провода ( l>> R ) из изотропного чистого металла температура T в стационарном случае будет зависеть только от радиальной переменной r ( 0 £ r £ R ) :
T=T(r). Из-за отсутствия радиального электрического тока
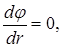 а а 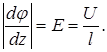
В итоге из (6) следует
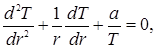 (9) (9)
где 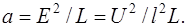
Уравнение (9) следует решать с дополнительными условиями :
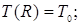 (10) (10)
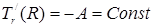 . (11) . (11)
( A > 0 )
Равенство (11) выражает постоянство теплового потока Q через боковую поверхность определённой длины 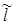 бесконечного цилиндра: бесконечного цилиндра:
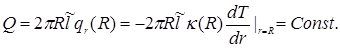 (12) (12)
Уравнение (9) с учётом (10) – (11) в качестве решения даёт радиальный профиль температуры T = T(r) , знание которого позволяет восстановить вольт-амперную характеристику ( ВАХ ) . Действительно, с учётом (8) ток
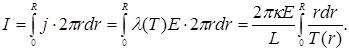 (13) (13)
Выражая величину 1/T из уравнения (9) и подставляя её в (13), получим после интегрирования
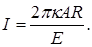 (14) (14)
В (14), как и в (11), константа А не является произвольной: в стационарном случае протекания тока всё выделяющееся в единицу времени джоулево тепло в конечном объёме бесконечно длинного проводника должно отводиться через боковую поверхность в окружающее пространство. Рассматривая длину 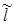 проводника, с учётом (11) и (12) будем иметь: проводника, с учётом (11) и (12) будем иметь:
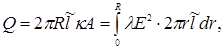 (15) (15)
или с учётом (8)
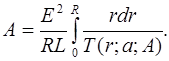 (16) (16)
Равенство (16) в неявной форме представляет зависимость константы А от 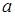 , так как решение T = T(r) уравнения (9) зависит через последнее от , так как решение T = T(r) уравнения (9) зависит через последнее от 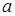 и через (11) от A. и через (11) от A.
Таким образом, если поддерживается постоянной температура Т0
боковой поверхности , то при стационарном протекании тока по проводнику в нём устанавливается такое распределение температуры T = T(r) по радиусу r, чтобы выполнялись равенства (9) – (11) и (16). Решение T = T(r) и константа А зависят от 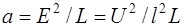 как от параметра, так что (13) или (14) представляют искомую вольт-амперную характеристику. При этом, как следует из уравнения (9), если как от параметра, так что (13) или (14) представляют искомую вольт-амперную характеристику. При этом, как следует из уравнения (9), если 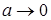 ( слабые поля ), то ( слабые поля ), то 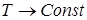 , т.е. согласно (13) , т.е. согласно (13) 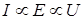 ( выполняется закон Ома (2) в интегральной форме ). При произвольных ( выполняется закон Ома (2) в интегральной форме ). При произвольных 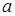 вследствие зависимости T = T(r) от вследствие зависимости T = T(r) от 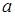 ВАХ (13) является в общем случае нелинейной. ВАХ (13) является в общем случае нелинейной.
В противоположном предельном случае 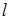 << R ( тонкий диск ) температура T зависит только от z: T = T(z), причём T(0) = T0
и T(l) = T1
. Обращаясь к уравнениям (6) – (7), получаем для T(z) следующее нелинейное интегро-дифференциальное уравнение: << R ( тонкий диск ) температура T зависит только от z: T = T(z), причём T(0) = T0
и T(l) = T1
. Обращаясь к уравнениям (6) – (7), получаем для T(z) следующее нелинейное интегро-дифференциальное уравнение:
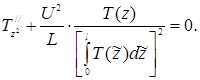 (17) (17)
При выводе (17) были использованы следующие из (7) равенства:
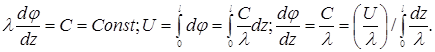
Вольт-амперная характеристика:
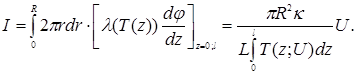 (18) (18)
В (18) T(z), являясь решением уравнения (17), зависит от U как от параметра. Поэтому ВАХ (18), вообще говоря, нелинейна
. В пределе 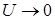 из (17) при T0
= T1
следует, что T = Const = T0
, т.е. (18) переходит в (2) – обычный закон Ома в интегральной форме. из (17) при T0
= T1
следует, что T = Const = T0
, т.е. (18) переходит в (2) – обычный закон Ома в интегральной форме.
Уравнения (9) и (17) являются нелинейными дифференциальным и интегродифференциальным уравнениями, которые следует решать численно с использованием средств компьютерной техники. Так, для решения уравнения (9) выбирается малый шаг h изменения радиальной переменной r, так что ( по Тэйлору ):

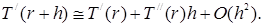 (19) (19)
В (19) 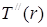 выражается из уравнения (9), поэтому выражается из уравнения (9), поэтому
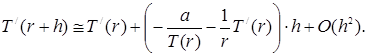 (20) (20)
Равенства (19) – (20) составляют ядро вычислительного алгоритма решения уравнения (9). При этом следует отметить, что константа А, определяющая 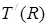 , для каждого значения , для каждого значения 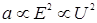 ищется методом подбора с целью удовлетворить равенству (16). В частности, задача (9) – (11), (16) может решаться методом последовательных приближений: сначала в (16) полагается T(r) = T0
, далее находится A и решается уравнение (9) с начальными условиями (10) – (11). Найденное решение ищется методом подбора с целью удовлетворить равенству (16). В частности, задача (9) – (11), (16) может решаться методом последовательных приближений: сначала в (16) полагается T(r) = T0
, далее находится A и решается уравнение (9) с начальными условиями (10) – (11). Найденное решение 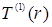 вновь подставляется в (16) и вся процедура повторяется до тех пор, пока не будет достигнута требуемая точность в определении величины А. вновь подставляется в (16) и вся процедура повторяется до тех пор, пока не будет достигнута требуемая точность в определении величины А.
Уравнение (17) можно решать методом итераций следующим образом. При малых напряжениях ( U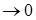 ), как следует из (17), ), как следует из (17),
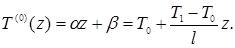 (21) (21)
С (21) вычисляется интеграл в (17):
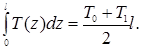 (22) (22)
Подставляя (22) в (17), получим ( уравнение гармонического осциллятора )
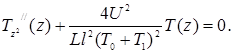 (23) (23)
Решением (23) на 1-ой итерации является
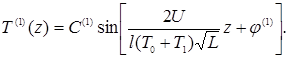 (24) (24)
Начальные условия T(0) = T0
и T(l) = T1
позволяют найти константы 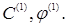 Вычисляя с (24) интеграл Вычисляя с (24) интеграл 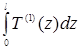 в (17), находим новое значение в (17), находим новое значение 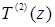 и т.д. Число итераций n можно ограничить требованием и т.д. Число итераций n можно ограничить требованием 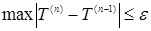 , где , где 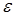 - наперёд заданная точность определения T, например, - наперёд заданная точность определения T, например, 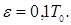
Итерационную процедуру необходимо осуществлять при каждом фиксированном значении U из определённого интервала 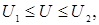 в котором и определяется ВАХ по формуле (18). в котором и определяется ВАХ по формуле (18).
В заключение следует подчеркнуть, что рассмотренная задача усложняется, если учитывать термодинамическую неравновесность и связанные с нею перекрёстные эффекты, как, например, перенос тепла не только за счёт механизма теплопроводности, но и за счёт дрейфа носителей заряда ( электронов ) под действием электрического поля (градиента потенциала) [1] . Кроме того, отвод тепла возможен и за счёт электро-магнитного излучения, что ещё в большей степени усложняет картину протекания электрического тока по металлическому протяжённому проводнику.
Задание
Найти радиальное распределение температуры металлического образца при прохождении электрического тока в случаях:
А) бесконечно длинного металлического проводника ( 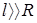 ) )
(значения 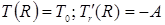 задаются по указанию преподавателя); задаются по указанию преподавателя);
В) короткого проводника большого диаметра (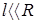 ) )
(значения 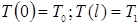 задаются по указанию преподавателя). задаются по указанию преподавателя).
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Ансельм А.И. Основы статистической физики и термодинамики. М., 1973.
2. Киттель Ч. Введение в физику твёрдого тела. М., 1978.
3. Сивухин Д.В. Общий курс физики. Электричество. М., 1977. Т.3.
|