| Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ГОУ ВПО «УГТУ - УПИ имени первого Президента России Б.Н. Ельцина»
СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ
Методические указания к лабораторной работе № 7
по курсам «Основы теории цепей», «Теория электрических цепей»
для студентов направлений «Радиотехника», «Телекоммуникации», «Информационная безопасность»
Екатеринбург 2008
Составители Е.В. Вострецова, Ю.В. Шилов
Научный редактор доц., канд. техн. наук А.П. Мальцев
СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ: Методические указания к лабораторной работе № 7 по курсам «Основы теории цепей», «Теория электрических цепей» /Е. В. Вострецова, Ю.В. Шилов. Екатеринбург, УГТУ-УПИ, 2008г.
Указания включают в себя описание лабораторной работы, посвященной исследованию частотных характеристик связанных колебательных контуров.
Описания работ содержат задания для выполнения расчетной части, методики проведения эксперимента, рекомендации по выполнению отчета.
Библиогр.: 5 назв. Рис.11
Подготовлено кафедрой “Теоретические основы радиотехники”.
© УГТУ-УПИ, 2008
1. Цель работы
Практическое знакомство и проверка правильности соотношений, описывающих амплитудно-частотные характеристики (АЧХ) двух индуктивно связанных контуров, изучение способов настройки системы связанных контуров.
2. Основные расчетные соотношения
На практике применяются колебательные контуры, энергия между которыми передается с использованием явления взаимной индукции. В таких контурах существует не один, а несколько резонансов.
Для характеристики «неполноты» включения реактивного элемента используется коэффициент включения
:
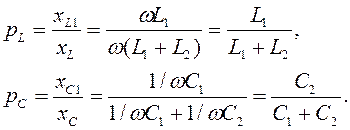
Коэффициент включения изменяется в пределах от нуля до единицы. В последнем случае рассматриваемый колебательный контур вырождается в параллельный колебательный контур основного вида.
В связи с тем, что одна из ветвей параллельного колебательного контура с неполным включением реактивного элемента представляет собой последовательное включение конденсатора и индуктивной катушки, в контуре этого вида наряду с резонансом токов имеет место резонанс напряжений.
Конструктивной особенностью колебательного контура этого вида является наличие в нем индуктивной катушки с отводом или со скользящим контактом, разделяющим катушку на две секции
Рассмотрим особенности частотных характеристик параллельного колебательного контура с неполным включением индуктивности и влияние коэффициента включения индуктивности рь
на параметры контура. Комплексное входное сопротивление рассматриваемого контура определяется выражением
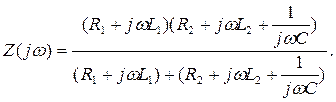
При высокой добротности элементах на частотах, близких к резонансной, входное сопротивление может быть определено по приближённой формуле:
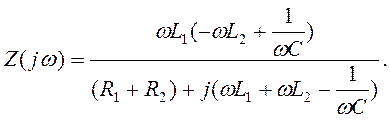
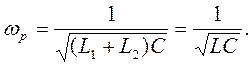
Частота резонанса токов параллельного колебательного контура 2-го вида не зависит от коэффициента включения индуктивности и совпадает с резонансной частотой последовательного колебательного контура, построенного из тех же элементов, что и рассматриваемый колебательный контур.
Частота резонанса напряжений w0
определяется только индуктивностью второй ветви L
2
и, следовательно, зависит от коэффициента включения индуктивности:
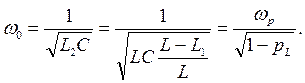
С уменьшением коэффициента включения индуктивности частота w0
уменьшается, оставаясь большей, чем wp
.
Cопротивление рассматриваемого контура на частоте резонанса токов:
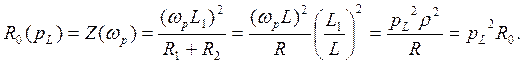
Здесь R =
R
1
+
R
2
- суммарное сопротивление потерь,
r
- характеристическое сопротивление рассматриваемого контура, равное характеристическому сопротивлению последовательного колебательного контура, составленного из тех же элементов,
R
0
=
r
2
/
R
— резонансное сопротивление параллельного контура основного вида.
Таким образом, резонансное сопротивление контура с неполным включением индуктивности R
0
(
pL
)
зависит от коэффициента включения и меньше, чем резонансное сопротивление контура основного типа R0
.
На частотах ниже wp
входное сопротивление контура определяется в основном сопротивлением ветви 1 и имеет резистивно-индуктивный характер. На частоте резонанса токов сопротивление контура достигает максимального значения R
0
(
pL
)
и имеет резистивный характер. На частотах выше w
p
сопротивление контура определяется в основном параметрами ветви 2, причем при w
p
<
w
<
w
0
сопротивление контура имеет резистивно-емкостной характер, а на частотах выше частоты резонанса напряжений резистивно-индуктивный. На частоте резонанса напряжений входное сопротивление контура имеет резистивный характер и достигает минимального значения, определяемого сопротивлением потерь второй ветви.
Добротность параллельного колебательного контура с неполным включением индуктивности не зависит от коэффициента включения и равна добротности последовательного колебательного контура, составленного из тех же элементов.
Колебательный контур этого типа по своим свойствам в значительной степени подобен параллельному колебательному контуру с неполным включением индуктивности. Используя эквивалентную схему контура, нетрудно показать, что частота резонанса токов w
p
, характеристическое сопротивление r
и добротность Q
параллельного колебательного контура с неполным включением емкости совпадают с резонансной частотой, характеристическим сопротивлением и добротностью последовательного колебательного контура, построенного из тех же элементов и, следовательно, обладающего теми же суммарной емкостью
Частота резонанса напряжений w0
рассматриваемого контура определяется параметрами элементов второй ветви
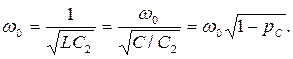
и зависит от коэффициента включения емкости.
Резонансное сопротивление контура с неполным включением емкости так же, как и резонансное сопротивление контура с неполным включением индуктивности, пропорционально квадрату коэффициента включения.
Итак, важнейшие параметры параллельного колебательного контура с неполным включением реактивного элемента (частота резонанса токов, характеристическое сопротивление и добротность) не зависят от коэффициента включения. Резонансное сопротивление контура является функцией pL
или p
С
.
Указанная особенность параллельного колебательного контура широко используется на практике при согласовании его с источником энергии. Согласование осуществляют путем надлежащего выбора значения коэффициента включения, причем при изменении коэффициента включения настройка контура и ширина его полосы пропускания, определяемые эффективной добротностью, не изменяются.
Наличие ярко выраженного минимума в АЧХ контура с неполным включением может быть использовано для подавления колебаний, частота которых близка к w0
рассматриваемого контура.
3. Расчетная часть
3.1. Для системы связанных контуров (рис. 1) рассчитайте емкости С
1
и С2
, считая, что оба контура настроены на резонансную частоту f
р
Все данные для расчетов (резонансная частота f
p
, индуктивности контуров L
1
и L
2
, сопротивление потерь первого контура RL
, внутреннее сопротивление источника тока Ri
) находятся в таблице в лаборатории.

Рис. 1. Эквивалентная схема исследуемой цепи
3.2. Для системы настроенных в резонанс связанных контуров рассчитайте и постройте нормированную зависимость напряжения на втором контуре U
2
/U
2
mm
от взаимной индуктивности М
, U
2
mm
– напряжение на втором контуре при полном резонансе. Укажите точки, в которых фактор связи А
равен 0.5, 1, 2. Определите взаимную индуктивность для этих факторов связи.
При расчетах считайте, что контуры имеют одинаковую добротность Q
, равную добротности первого контура, зашунтированного внутренним сопротивлением источника тока Ri
(pиc. 1).
Расчетные соотношения имеют вид:

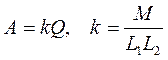
где k - коэффициент связи между контурами.
3.3. Рассчитайте и постройте на одном рисунке нормированные АЧХ – зависимости напряжения на втором контуре U
2
/U
2
mm
от частоты f
для факторов связи 0.5, 1, 2.
3.4. Обоснуйте справедливость расчетной формулы из п. 3.1.5 для высокодобротных катушек.
3.5. Изучите порядок выполнения работы.
4. Экспериментальная часть
Работе выполняется не блоке "Избирательные цепи".
4.1. Изучение зависимости взаимной индуктивности М
от расстояния между катушками.
4.1.1. Соберите схему согласно рис. 2. Включите питание измерительных приборов и лабораторного стенда.
4.1.2. Подайте от генератора колебание с заданной частотой, равной резонансной частоте первого контура fp
, и амплитудой 0,1…0,5 В.
4.1.3. Разведя катушки на максимальное расстояние (20…25 мм), произведите настройку первого контура в резонанс по максимуму напряжения U2,
изменяя емкость С1
Напряжение на контуре должно быть гармоническим. Если его вид искажается при настройке, необходимо уменьшить амплитуду выходного колебания генератора.
4.1.4. Снимите зависимость напряжений на катушках от расстояния между ними U1
(x), U2
(x). Расстояние между катушками изменяйте в интервале от 0 до 20…25мм с шагом 2мм.
4.1.5. Рассчитайте и постройте зависимость М(х):
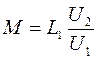 . .

Рис. 2. Схема установки для измерения взаимной индуктивности/ ГЕН – генератор, ИП – измерительный прибор (вольтметр или осциллограф), ОСЦ - осциллограф
4.2. Настройка контуров.
Для получения качественных результатов необходимо соблюдать аккуратность: после настройки контуров нельзя отключать от схемы измерительные приборы (или подключать дополнительные), изменять емкости контуров.
4.2.1. Соберите схему согласно рис. 3. От генератора подайте колебание с частотой fp
и амплитудой 0,1…0,5 В.
4.2.2. Разведите катушки на максимальное расстояние (20…25мм). Разомкните контур L2
C2
, т.е. емкость С2
отключите, а осциллограф подключите к катушке L2
.
4.2.3. Изменяя емкость С
1
, настройте первый контур в резонанс по максимуму напряжения U
2
Примечание. Напряжение на контуре должно быть гармоническим. Если его вид искажается при настройке, необходимо уменьшить амплитуду выходного колебания ГВЧ.
4.2.4. Замкните контур L2
C2.
Изменяя емкость С2
, настройте второй контур в резонанс по максимуму напряжения U2
Рис. 3. Схема установки для измерения АЧХ
4.3. Определение зависимости U2
(M)
4.3.1. Снимите зависимость U
2
(x
) в интервале от 0 до 20…25мм с шагом 2 мм. Постройте график U2
(x), обозначьте точки, где фактор связи А
= 0.5, 1, 2.
4.3.2. Пользуясь зависимостью М(х), снятой в п. 3.1, постройте график U
2
/U
2
mm
(М
).
4.4. Измерение АЧХ системы связанных контуров.
Все АЧХ необходимо снимать в интервале частот oт f
min
до f
max
, где f
min
и f
max
выбираются из условия
U
2
(f
min
) = U2
(f
max
) = 0.2U
2mm,
где U
2
mm
- напряжение на втором контуре при полном резонансе.
4.4.1. Установите значение х
, соответствующее фактору связи А
= 1. Изменяя частоту генератора, снимите зависимость напряжения на втором контуре U
2
от частоты f
.
При измерениях амплитуду выходного колебания генератора поддерживайте постоянной.
4.4.2. Повторите измерение АЧХ пo п 3.4.1 для факторов связи А = 0.5 и А = 2.
5. Обработка результатов
В отчете должны быть приведены все графики, рассчитанные при подготовке к работе и полученные в ходе эксперимента.
5.1. Постройте на одном рисунке графики U
2
/U
2
mm
(М
): рассчитанный при подготовке к работе и полученный в ходе эксперимента.
5.2. Рассчитайте по результатам эксперимента нормированные АЧХ U
2
/U
2
mm
(f
), где U
2
mm
- напряжение на втором контуре при полном резонансе. Построите их на одном рисунке для трех факторов связи в едином масштабе. На графиках укажите резонансную частоту, фактор связи, определите полосы пропускания для трех факторов связи.
5.3. Сформулируйте выводы по проделанной работе.
6. Требования к содержанию отчета
Отчёт должен содержать:
6.1. цель работы;
6.2. расчётную часть (исходные данные, расчётные формулы с пояснениями, результаты расчётов);
6.3. схемы измерений;
6.4. таблицы экспериментальных результатов;
6.5. графики АЧХ;
6.6. выводы.
7. Контрольные вопросы
7.1 Какие резонансы могут быть в системе связанных контуров и при каких условиях?
7.2 Объясните порядок настройки контуров в полный резонанс
7.3 Оба контура системы настроены на частоту генератора. Как по графику зависимости напряжения на втором контуре от связи между контурами определить фактор связи А ?
7.4 Объясните наличие двух максимумов у резонансной кривой при А>1, пользуясь понятием вносимых сопротивлений.
7.5 В системе связанных контуров в результате настройки первого контура получен максимум тока I1
Будет ли при этом максимум тока во втором контуре?
7.6 В системе связанных контуров в результате настройки второго контура получен максимум тока I2.
Будет ли при этом максимум тока в первом контуре?
7.7 Нарисуйте семейство фазовых характеристик связанных одинаковых колебательных контуров при факторах связи А = 0.5, 1, 2.
7.8 Систему двух связанных контуров с трансформаторной связью называют иногда резонансным трансформатором. Покажите справедливость этой аналогии.
7.9 В системе двух связанных контуров полный резонанс. Емкость первого контура уменьшилась. Как изменится резонансная кривая тока второго контура?
7.10 В системе двух связанных контуров полный резонанс при А=1; ток второго контура I2
= 100 мА. Произошел разрыв цепи второго контура. Каким будет при этом ток первого контура?
Библиографический список
1. Попов В.П. Основы теории цепей. - М.: Высшая школа, 2003.
2. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: Высшая школа, 2003.
3. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. – М.: Радио и связь, 2001.
4. Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1994.
5. Бирюков В.Н., Попов В.П., Семенцов В.И. Сборник задач по теории цепей. - М.: Высшая школа, 1998.
6. Баскаков С. И. Радиотехнические цепи и сигналы: Руководство к решению задач: сборник задач. Высшая школа, 2002.
Методические разработки кафедры
1. Вострецова Е.В. Основы теории цепей. Методические указания по выполнению лабораторных работ. Часть 1. г. Екатеринбург, ГОУ ВПО УГТУ-УПИ, 2005.
2. Вострецова Е.В. Основы теории цепей. Методические указания по выполнению лабораторных работ. Часть 2. г. Екатеринбург, ГОУ ВПО УГТУ-УПИ, 2005.
3. Вострецова Е.В, Ковалев Е.И. Основы теории цепей. Методические указания к лабораторным работам 9,10. ГОУ ВПО УГТУ-УПИ. г. Екатеринбург, 2005.
4. Ковалев Е.И., Лучинин А.С., Мальцев А.П. Исследование нелинейных цепей: Методические указания к лабораторным работам. Екатеринбург: УГТУ-УПИ, 2002.
5. Лысенко Т.М. Анализ линейной активной цепи: Мет. указ. к курсовой работе. Екатеринбург, Изд-во УГТУ, 2007.
6. Зраенко С.М. Теория электрических цепей: Мет. указ. к практическим занятиям. Ч. 1. Екатеринбург, Изд-во УГТУ, 2006.
|