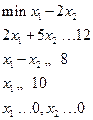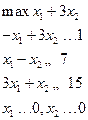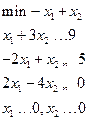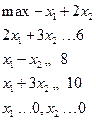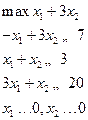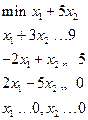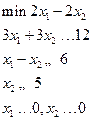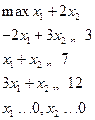Аннотация

Учебное пособие содержит задания к лабораторным работам по курсу «Экономико-математическое моделирование», состоящие в разработке и экономическом анализе решений несложных, но содержательных в экономическом отношении оптимизационных и эконометрических моделей. Отрабатывается использование анализа «затраты-выпуск», методов линейного и нелинейного программирования, элементарные параметрические и непараметрические методы эконометрики. Задания ориентированы на приобретение навыков взаимодействия с экономистами-математиками в процессе решения задач по управлению хозяйственными комплексами различного масштаба и уровня сложности.

Введение

Представленный в настоящем издании цикл заданий предназначен для проведения лабораторных работ во время аудиторных занятий по курсу «Экономико-математическое моделирование» объёмом 60-70 часов аудиторных занятий. Предполагается, что на выполнение лабораторного практикума затрачивается примерно половина времени аудиторных занятий по данному курсу — в среднем по 3 часа на одну лабораторную работу.

Особенность предлагаемых заданий состоит в том, что они обеспечивают достаточную практическую подготовку по изучаемому курсу выпускникам вузов, профессия которых не требует самостоятельной разработки оригинальных экономико-математических моделей либо руководства такой разработкой. Однако приобретаемые навыки обеспечивают успешное взаимодействие с экономистами-математиками в процессе решения задач по управлению хозяйственными комплексами различного масштаба и уровня сложности, а также позволяют эффективно работать с экономической литературой, содержащей математическую нотацию и числовые примеры.

При разработке заданий автор опирался на классическую структуру курса «Экономико-математическое моделирование», но при этом стремился насытить её наиболее содержательными приёмами математического моделирования, трудоёмкость которых ещё допускает их освоение в формате лабораторной работы. Так, в данное пособие включены лабораторные работы по моделированию инвестиционного портфеля, размещения производства по филиалам, по анализу технологической эффективности фирм при помощи метода оболочки данных.

За рядом вполне естественных исключений, задания построены таким образом, чтобы они не представляли собой условные расчётные примеры, а имели очевидный студенту экономический смысл, приводя к конкретным предложениям по подготовке и принятию хозяйственных решений. По замыслу составителя, лабораторные работы должны стимулировать критическое отношение к осваиваемым математическим методам, формировать понимание границ их применимости.

Лабораторные работы не имеют сквозного характера, выполняются независимо одна от другой и потому могут дополнять практические курсы, построенные на основе учебных материалов других авторов, в том числе по более объёмным курсам. Если, напротив, на изучение данного курса выделено меньшее количество часов либо сочетание объёмов теоретического и практического курсов отличается от рекомендуемого в пользу изложения теоретического материала, преподаватель может опустить некоторые лабораторные работы либо отдельные их задания.

Студенты должны ознакомиться с содержанием лабораторной работы заранее во время самостоятельной подготовки, причём обязательно после освоения теоретического материала (лекций и рекомендуемой литературы) по соответствующей теме. Если отдельные положения заданий или методических указаний к ним студенту не вполне понятны, он должен обратиться к преподавателю с вопросом до начала лабораторной работы. При выполнении этих требований и в отсутствие нештатных ситуаций (например, компьютерных сбоев) для выполнения лабораторного практикума в полном объёме не требуется внеаудиторной работы (помимо подготовительной).

Как правило, лабораторные работы должны выполняться в компьютерном классе. При этом на одного преподавателя (включая ассистентов и стажёров) должно приходиться не более десяти-двенадцати студентов. В противном случае эффективность выполнения лабораторных работ снижается, так как студентам приходится ожидать пояснений преподавателя при возникновении затруднительных ситуаций. При подобных обстоятельствах студентам приходится завершать выполнение лабораторных работ во время самостоятельной подготовки.

Лабораторная работа №1.
Модели межотраслевого баланса

Цель работы : приобрести элементарные практические навыки экономических расчётов при помощи моделей межотраслевого баланса.

Приборы и материалы : одно из нижеперечисленного: микрокалькулятор; КПК, оснащённый табличным процессором; ПЭВМ, оснащённая табличным процессором.

Задание

1. На основании данных таблицы «Затраты-выпуск» (см. индивидуальные варианты задания 1 ниже) рассчитать коэффициенты прямых и полных затрат.

2. На основании данных таблицы коэффициентов прямых затрат (см. индивидуальные варианты задания 2 ниже) рассчитать:

¨ коэффициенты полных затрат;

¨ объёмы валовой продукции, обеспечивающие заданный чистый выпуск;

¨ таблицу «Затраты-выпуск»;

¨ цены, обеспечивающие производство в каждой отрасли заданной добавленной стоимости.

3. Оформить отчёт.

Методические указания по выполнению задания

Вычисление обратной матрицы можно выполнить любым из известных вам методов (например, метод присоединённой матрицы, метод алгебраических дополнений) или с помощью функции МОБР табличного процессора Microsoft Excel. Для проверки правильности вычисления обратной матрицы умножьте её на исходную.

Требования к отчёту

Помимо индивидуального варианта задания, алгоритма решения и ответа, в отчёте следует представить проверку правильности проведённых вычислений и экономическую интерпретацию результатов расчётов (всюду, где она возможна).

Если преподавателем не предписано иначе, отчёт предоставляется в электронном виде на дискете или с использованием средств компьютерных телекоммуникаций.

Литература

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2‑е изд. М.: ЮНИТИ-ДАНА, 2005. — п.6.1…6.4.

Варианты заданий

Таблицы «Затраты-выпуск» к заданию 1

Коэффициенты прямых затрат к заданию 2

Лабораторная работа №2.
Практикум по решению задач линейного программирования

Цель работы : овладеть практическими навыками решения задач линейного программирования симплексным методом.

Приборы и материалы : линейка, угольник (или циркуль), карандаш; микрокалькулятор либо КПК, оснащённый табличным процессором; ПЭВМ, оснащённая табличным процессором; программа линейной оптимизации Sunset XA.

Задание

1. Решить графическим методом задачу линейного программирования согласно индивидуальному варианту (см. ниже).

2. Составить и решить симплексным методом задачу линейного программирования (с учётом изменений, предусмотренных индивидуальным вариантом задания), предназначенную для составления оптимальной производственной программы молокоперерабатывающего предприятия при следующих условиях.

¨ Ассортимент выпускаемой продукции включает пастеризованное молоко, кефир и сметану, а также дополнительную продукцию согласно индивидуальному варианту задания.

¨ Затраты сырого молока составляют:

¨ На пастеризованное молоко – 1,01 кг/кг;

¨ На кефир – 1,01 кг/кг;

¨ На сметану – 9,45 кг/кг.

¨ Поставщики в состоянии поставить не более 140 ц молока в сутки.

¨ Фасовка молока и кефира осуществляется на автоматизированной линии производительностью 5 ц молока или 6 ц кефира в час. В течение суток линия может эксплуатироваться не более 21 часа.

¨ Фасовка сметаны осуществляется на другой автоматизированной линии производительностью 30 кг сметаны в час. В течение суток линия может эксплуатироваться не более 16 часов.

¨ Цена реализации пастеризованного молока – 2,4, кефира – 2,7, сметаны – 13,8 тыс. руб./ц.

¨ План должен обеспечивать максимальную выручку от реализации молочной продукции (контракт на поставку молока уже оплачен).

3. Оформить отчёт.

Методические указания по выполнению задания

При выполнении задания 2 необходимо предусмотреть:

¨ переменные по выпуску продукции каждого вида;

¨ ограничения по использованию сырого молока и по времени загрузки автоматизированных фасовочных линий,

¨ другие ограничения и переменные согласно индивидуальным вариантам задания.

Задачу следует решать симплексным методом. Разрешается либо получить опорное решение методом искусственного базиса, либо использовать метод последовательного наложения ограничений, рассмотренный в лекции.

Рекомендуется по завершении расчётов выполнить проверку правильности численного решения с использованием программных средств линейной оптимизации.

Требования к отчёту

По заданию 1 в отчёте должны быть представлены чертежи, поясняющие решение задачи линейного программирования графическим методом.

По заданию 2 в отчёте следует привести:

¨ математическую запись задачи линейного программирования с указанием названий и единиц измерения переменных и ограничений;

¨ исходную симплексную таблицу;

¨ все промежуточные симплексные таблицы;

¨ заключительную симплексную таблицу;

¨ оптимальное решение, оптимальное значение целевой функции и экономическую интерпретацию оптимального плана.

Если иное не предписано преподавателем, отчёт сдаётся в электронном виде на дискете или с помощью средств электронных телекоммуникаций. Допускается рукописное приложение к отчёту, содержащее решение задания 1.

Литература

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2‑е изд. М.: ЮНИТИ-ДАНА, 2005. — гл.2.

Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.

Светлов Н.М. , Светлова Г.Н. Построение и решение оптимизационных моделей средствами программ MS Excel и XA / РГАУ – МСХА им. К.А. Тимирязева. М.: 2005.

Варианты заданий

К заданию 1

К заданию 2

1. Дополнительный вид продукции — творог. Цена — 5200 руб./ц. Затраты сырого молока — 17 ц/ц. Производительность фасовки на оборудовании для фасовки творога — 0,8 ц/ч. Оборудование может работать не более 16 ч./сут.

2. Дополнительный вид продукции — йогурт. Цена — 2200 руб./ц. Затраты сырого молока — 0,9 ц/ц. Производительность фасовки на оборудовании для фасовки сметаны — 0,2 ц/ч. Максимальный выпуск — 20 ц/сут.

3. Дополнительный вид продукции — творожные сырки. Цена — 7200 руб./ц. Затраты сырого молока — 15 ц/ц. Производительность фасовки на оборудовании для фасовки творожных сырков — 0,2 ц/ч. Оборудование может работать не более 16 ч./сут.

4. Дополнительный вид продукции — кефир обезжиренный. Цена — 770 руб./ц. Затраты сырого молока — 0,3 ц/ц. Производительность фасовки на оборудовании для фасовки молока и кефира — 6 ц/ч. Суммарный максимальный выпуск кефира обоих видов — 40 ц/сут. (минимальный выпуск кефира жирного не регламентируется).

5. Дополнительный вид продукции — творог. Цена — 5500 руб./ц. Затраты сырого молока — 18 ц/ц. Производительность фасовки на оборудовании для фасовки творога — 0,3 ц/ч. Оборудование может работать не более 16 ч./сут.

6. Дополнительный вид продукции — йогурт. Цена — 2000 руб./ц. Затраты сырого молока — 0,8 ц/ц. Производительность фасовки на оборудовании для фасовки сметаны — 0,2 ц/ч. Максимальный выпуск — 12 ц/сут.

7. Дополнительный вид продукции — творожные сырки. Цена — 7800 руб./ц. Затраты сырого молока — 14 ц/ц. Производительность фасовки на оборудовании для фасовки творожных сырков — 0,25 ц/ч. Оборудование может работать не более 18 ч./сут.

8. Дополнительный вид продукции — кефир обезжиренный. Цена — 790 руб./ц. Затраты сырого молока — 0,31 ц/ц. Производительность фасовки на оборудовании для фасовки молока и кефира — 6 ц/ч. Доля обезжиренного кефира в общем производстве кефира должна составлять не менее трети.

9. Дополнительный вид продукции — творог. Цена — 5300 руб./ц. Затраты сырого молока — 17 ц/ц. Производительность фасовки на оборудовании для фасовки творога — 0,4 ц/ч. Оборудование может работать не более 16 ч./сут.

10. Дополнительный вид продукции — йогурт. Цена — 2500 руб./ц. Затраты сырого молока — 0,85 ц/ц. Производительность фасовки на оборудовании для фасовки сметаны — 0,15 ц/ч. Йогурта должно производиться не меньше, чем сметаны.

11. Дополнительный вид продукции — творожные сырки. Цена — 7500 руб./ц. Затраты сырого молока — 16 ц/ц. Производительность фасовки на оборудовании для фасовки творожных сырков — 0,25 ц/ч. Оборудование может работать не более 17 ч./сут.

12. Дополнительный вид продукции — кефир обезжиренный. Цена — 770 руб./ц. Затраты сырого молока — 0,27 ц/ц. Производительность фасовки на оборудовании для фасовки молока и кефира — 5.5 ц/ч. Суммарный минимальный выпуск кефира обоих видов — не более 8 ц/сут.

13. Дополнительный вид продукции — творог. Цена — 5400 руб./ц. Затраты сырого молока — 13 ц/ц. Производительность фасовки на оборудовании для фасовки творога — 0,35 ц/ч. Оборудование может работать не более 17 ч./сут.

14. Дополнительный вид продукции — йогурт. Цена — 2750 руб./ц. Затраты сырого молока — 0,95 ц/ц. Производительность фасовки на оборудовании для фасовки сметаны — 0,25 ц/ч. Максимальный выпуск — 15 ц/сут.

15. Дополнительный вид продукции — творожные сырки. Цена — 7700 руб./ц. Затраты сырого молока — 19 ц/ц. Производительность фасовки на оборудовании для фасовки творожных сырков — 0,2 ц/ч. Оборудование может работать не более 20 ч./сут.

16. Дополнительный вид продукции — кефир фруктовый. Цена — 1080 руб./ц. Затраты сырого молока — 0,57 ц/ц. Производительность фасовки на оборудовании для фасовки молока и кефира — 5,5 ц/ч. Фруктового кефира должно выпускаться не меньше, чем обычного.

17. Дополнительный вид продукции — творог с изюмом. Цена — 6400 руб./ц. Затраты сырого молока — 13 ц/ц. Производительность фасовки на оборудовании для фасовки творога — 0,15 ц/ч. Оборудование может работать не более 18 ч./сут.

18. Дополнительный вид продукции — молочный коктейль. Цена — 2050 руб./ц. Затраты сырого молока — 0,95 ц/ц, сахара — 4 кг/ц. Суточный ресурс сахара составляет 60 кг. Производительность фасовки на оборудовании для фасовки молока и кефира — 0,5 ц/ч.

19. Дополнительный вид продукции — творожные сырки. Цена — 7300 руб./ц. Затраты сырого молока — 17,5 ц/ц. Производительность фасовки на оборудовании для фасовки творожных продуктов — 0,15 ц/ч. Оборудование может работать не более 18 ч./сут.

20. Дополнительный вид продукции — кефир фруктовый. Цена — 1180 руб./ц. Затраты сырого молока — 0,87 ц/ц. Производительность фасовки на оборудовании для фасовки молока и кефира — 6 ц/ч. В ассортименте кефира фруктовый кефир должен составлять не менее 60%.

Лабораторная работа №3.
Теория двойственности. Экономический анализ оптимального плана

Цель работы : овладеть практическими навыками решения задач линейного программирования симплексным методом.

Приборы и материалы : ПЭВМ, оснащённая табличным процессором; программа линейной оптимизации Sunset XA.

Задание

1. Составить и решить симплексным методом задачу, двойственную к задаче, соответствующей индивидуальному варианту задания 2 лабораторной работы №2.

2. При помощи полученного решения:

¨ определить максимальную цену, по которой выгодно покупать молочное сырьё;

¨ рассчитать максимально приемлемый уровень затрат на сокращение нерабочего периода каждого из фасовочных автоматов на 3%.

3. На основе полученного решения двойственной задачи определить, выгодным ли окажется производство нового продукта — обезжиренного молока, если затраты сырого молока на 1 ц обезжиренного составляют 0,1 ц, производительность его упаковки на оборудовании для фасовки молока и кефира — 7 ц/ч, цена — 300 руб./ц.

4. Оформить отчёт.

Методические указания по выполнению задания

Рекомендуется по завершении расчётов выполнить проверку правильности численного решения с использованием программных средств линейной оптимизации.

Требования к отчёту

По заданию 1 в отчёте должны быть представлены:

¨ математическая запись двойственной задачи линейного программирования с указанием названий и единиц измерения переменных и ограничений;

¨ исходная симплексная таблица;

¨ заключительная симплексная таблица;

¨ оптимальное решение и оптимальное значение целевой функции.

По заданию 2 в отчёте должны быть отражены расчёты и их результат.

По заданию 3 в отчёте требуется представить заключение о целесообразности производства обезжиренного молока, обоснованное расчётами.

Если иное не предписано преподавателем, отчёт сдаётся в электронном виде на дискете или с помощью средств электронных телекоммуникаций.

Литература

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2‑е изд. М.: ЮНИТИ-ДАНА, 2005. — гл.3.1.

Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.

Светлов Н.М. , Светлова Г.Н. Построение и решение оптимизационных моделей средствами программ MS Excel и XA / РГАУ – МСХА им. К.А. Тимирязева. М.: 2005.

Лабораторная работа № 4 .
Оптимизация портфеля ценных бумаг с использованием линейного программирования

Цель работы : овладеть практическими навыками формализации задач об оптимальном портфеле ценных бумаг и их решения с помощью соответствующих программных средств.

Приборы и материалы : ПЭВМ, оснащённая табличным процессором; программа линейной оптимизации Sunset XA.

Задание

Составить и решить симплексным методом задачу в соответствии с нижеследующими условиями и данными индивидуального варианта задания.

Перед консалтинговой фирмой ЗАО «Клиент-симплекс» стоит задача сформировать портфель ценных бумаг, обеспечивающий доход, достаточный для финансирования операционной деятельности хотя бы в минимальном объёме (не менее 20 млн. руб./год) при вероятных сочетаниях конъюнктурных факторов, определяющих доходность ценных бумаг каждого вида.

В настоящее время ЗАО «Клиент-симплекс» располагает акциями коммерческого банка «Фортуна» на сумму 500 млн. руб. и свободными денежными средствами в размере 1 млрд. руб. Аналитики организации сгруппировали вероятные сочетания конъюнктурных факторов в пять групп с примерно одинаковой доходностью каждой из наиболее ликвидных ценных бумаг, обращающихся на рынке. Данные о доходности приведены в табл. 1.

Требуется сформировать такой портфель ценных бумаг, который при любой возможной конъюнктуре обеспечивает доход не менее 20 млн. руб. и приносит максимальную величину среднего ожидаемого дохода с учётом вероятностей каждого варианта конъюнктуры, принимая во внимание, что акции КБ «Фортуна» на рынке отсутствуют (следовательно, их можно только продавать, если в этом есть необходимость), а другие акции доступны на бирже в количествах, определённых индивидуальными вариантами задания.

Таблица 1

Доходность ценных бумаг, котирующихся на бирже,
участником которой является ЗАО «Клиент-симплекс», % годовых

Примечание . Сведения о вероятности наступления каждого варианта конъюнктуры приведены в индивидуальных вариантах.

При помощи полученного решения определить максимальную процентную ставку, под которую ещё выгодно финансировать операционную деятельность за счёт кредита вместо обеспечения минимального уровня доходности пакета ценных бумаг.

Оформить отчёт.

Методические указания по выполнению задания

Математическая модель должна содержать переменные, обозначающие количество акций каждого вида (млн. руб.), и три группы ограничений: баланс инвестиционных ресурсов (млн. руб.); доходность портфеля при каждом варианте конъюнктуры (млн. руб.); максимальный объём покупки или продажи акций (млн. руб.).

Номиналы акций при решении задачи не принимаются во внимание (предполагается, что они достаточно малы). Следовательно, нет необходимости вводить требование целочисленности переменных модели.

Требования к отчёту

В отчёте должны быть представлены:

¨ математическая запись задачи линейного программирования с указанием названий и единиц измерения переменных и ограничений;

¨ оптимальное решение (значения переменных) и оптимальное значение целевой функции;

¨ суммы и двойственные оценки ограничений;

¨ оптимальные оценки переменных;

¨ аргументированный ответ на вопрос задания 2.

Если иное не предписано преподавателем, отчёт сдаётся в электронном виде на дискете или с помощью средств электронных телекоммуникаций.

Литература

Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. — 2‑е изд. М.: Финансы и статистика, 2005. — п.2.2.8.

Светлов Н.М. , Светлова Г.Н. Построение и решение оптимизационных моделей средствами программ MS Excel и XA / РГАУ – МСХА им. К.А. Тимирязева. М.: 2005.

Варианты заданий

Таблица 2

Варианты заданий лабораторной работы №4

Лабораторная работа №5.
Размещение производства по филиалам

Цель работы : овладеть практическими навыками формализации задач о размещении производства и их решения с помощью соответствующих программных средств.

Приборы и материалы : ПЭВМ, оснащённая табличным процессором; программа линейной оптимизации Sunset XA.

Задание

Составить и решить следующую задачу, изменив нижеприведённое условие в соответствии с индивидуальным вариантом задания.

ЗАО «Галактика», занимающееся переработкой молока, имеет в своём составе предприятия (филиалы) в трёх административных районах, каждое из которых выпускает пастеризованное молоко, кефир и сметану. Данные о производстве сырого молока в каждом районе фермерами, имеющими договорные связи с ЗАО «Галактика», об объёмах рынка каждого вида продукции[1] и о средней дальности перевозок представлены в табл. 3. Данные о нормах расхода сырого молока для производства каждого вида продукции, о производительности оборудования для фасовки продукции, времени его работы и о ценах её реализации приведены в задании к лабораторной работе №8. Избыток произведённого пастеризованного молока может быть реализован в г. Рязань, расположенном на расстоянии 100 км от Клепиковского района. Фермеры, имеющие договоры с ЗАО «Галактика», поставляют ему молочное сырьё по цене 11 тыс. руб./т[2] . Недостаток молочного сырья можно компенсировать за счёт приобретения его у производителей, не имеющих твёрдых договоров с ЗАО «Галактика», по цене 17 тыс. руб./т.

Определить оптимальный план размещения производства молочных продуктов по филиалам при условии, что в целях недопущения конкурентов на локальный рынок имеющийся спрос должен быть удовлетворён в полном объёме.

Таблица 3

Исходные данные к задаче о размещении производства по филиалам

Методические указания по выполнению задания

Рекомендуемый набор переменных (без учёта изменений в соответствии с индивидуальным вариантом задания): объёмы производства молока, кефира и сметаны в каждом районе, т (9); объём поставок сырья по договорам в каждом регионе, т (3); объём поставок сырья сверх договоров в каждом регионе, т (3); межрайонные перевозки молочного сырья, т (4); межрайонные перевозки каждого вида продукции, т (12); реализация пастеризованного молока в Рязани, т (1).

Рекомендуемый набор ограничений: баланс молочного сырья в каждом районе, т (3); использование рабочего времени каждого вида оборудования в каждом районе, ч (6); баланс молочной продукции каждого вида в каждом районе, т (9).

Объёмы спроса на молочную продукцию каждого вида в каждом районе рекомендуется представить в форме свободных членов балансов молочной продукции.

При разработке экономико-математической модели не забудьте проверить корректность единиц измерения переменных и параметров ограничений и целевой функции.

Требования к отчёту

В отчёте должны быть представлены:

¨ математическая запись экономико-математической модели с указанием названий и единиц измерения переменных и ограничений;

¨ оптимальное решение (значения переменных) и оптимальное значение целевой функции;

¨ значения дополнительных переменных и двойственных оценок ограничений модели;

¨ план производства, перевозок и реализации сырья и продукции ЗАО «Галактика»;

¨ рекомендации по перспективам развития молочного производства ЗАО «Галактика», основанные на результатах решения экономико-математической модели.

Если иное не предписано преподавателем, отчёт сдаётся в электронном виде на дискете или с помощью средств электронных телекоммуникаций.

Литература

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — разделы 2.5, 3.1.

Варианты заданий (цифры в скобках – контрольное значение целевой функции в тыс. руб.)

1. В Клепиковском районе имеются две линии по фасовке сметаны. Перевозка молочного сырья не предусматривается (343,56 ).

2. В Касимовском районе имеются две линии по фасовке сметаны. Цена сметаны – 12 тыс. руб./ц. Перевозка кефира не предусматривается (317,12 ).

3. В Шиловском районе имеются две линии по фасовке сметаны. Не предусматривается перевозка пастеризованного молока, кроме вывоза его из Клепиковского района в Рязань (342,85 ).

4. Линии по фасовке сметаны могут работать по 20 часов. Перевозка сметаны не предусматривается. В Клепиковском районе по договорам с фермерами может быть заготовлено 6,5 т молочного сырья в сутки (350,19 ).

5. В Клепиковском районе имеются две линии по фасовке сметаны. Цена кефира составляет 2,5 тыс.руб./ц, при этом его перевозка не предусматривается (333,16 ).

6. В Касимовском районе имеются две линии по фасовке сметаны. Цена пастеризованного молока – 2,5 тыс. руб./ц. Перевозка пастеризованного молока, за исключением его доставки из Клепиковского района в Рязань, не предусматривается (370,37 ).

7. В Шиловском районе имеются две линии по фасовке сметаны. Затраты на 1 т·км перевозки молочного сырья составляют 52 руб. Перевозки пастеризованного молока не предусматриваются (331,51 ).

8. Линии по фасовке сметаны могут работать по 18 часов. Перевозка пастеризованного молока не предусматривается, за исключением поставок из Клепиковского района в Рязань. Цена молока в Рязани составляет 2,0 тыс.руб./ц. (331,71 ).

9. В Клепиковском районе имеются две линии по фасовке сметаны. Перевозка молочного сырья не предусматривается. Затраты на перевозку сметаны составляют 57 руб./(т·км). (343,47 ).

10. В Касимовском районе имеются две линии по фасовке сметаны. Затраты молочного сырья на производство кефира составляют 0,9 т/т. Перевозка кефира не предусматривается (353,85 ).

11. В Шиловском районе имеются две линии по фасовке сметаны. Перевозки пастеризованного молока не предусматриваются, за исключением поставок из Клепиковского района в Рязань. В Шиловском районе молочное сырьё может закупаться только по договорам (324,49 ).

12. Линии по фасовке сметаны могут работать по 18 часов. Перевозка кефира не предусматривается. В Клепиковском районе сырое молоко может быть заготовлено только в договорных объёмах (311,86 ).

13. В Клепиковском районе имеются две линии по фасовке сметаны. Перевозка пастеризованного молока не предусматривается. Цена молочного сырья, приобретаемого сверх договоров, составляет 15 руб./кг в Касимовском районе и 12 руб./кг в остальных (399,15 ).

14. В Касимовском районе имеются две линии по фасовке сметаны. Перевозка молочного сырья не предусматривается из-за отсутствия специализированного транспорта. Максимальный суточный объём поставок пастеризованного молока в Рязань составляет 3 т (339,77 ).

15. В Шиловском районе имеются две линии по фасовке сметаны. Перевозки пастеризованного молока не предусматриваются, за исключением поставок из Клепиковского района в Рязань. Суточный ресурс работы оборудования для фасовки молока и кефира составляет 20 ч (336,93 ).

16. Линии по фасовке сметаны могут работать по 18 часов. Перевозки молочного сырья и поставка пастеризованного молока в Рязань не предусматриваются. Все транспортные затраты снижаются на 10% по сравнению с базовым вариантом (333,11 ).

17. В Клепиковском районе имеются две линии по фасовке сметаны. Перевозка пастеризованного молока не предусматривается, за исключением поставок из Клепиковского района в Рязань. Максимальный суточный объём поставок пастеризованного молока в Рязань составляет 2,5 т (337,13 ).

18. В Касимовском районе имеются две линии по фасовке сметаны. Ресурс рабочего времени оборудования для фасовки сметаны составляет 17 ч в сутки. Перевозка кефира не предусматривается. Цена молочного сырья, приобретаемого сверх договоров, составляет 15 руб./кг в Клепиковском районе и 12 руб./кг в остальных (421,10 ).

19. В Шиловском районе имеются две линии по фасовке сметаны. В Клепиковском районе отсутствует оборудование для фасовки молока и кефира, зато в Касимовском районе функционируют два комплекта такого оборудования. Перевозки пастеризованного молока не предусматриваются, кроме его доставки из Касимовского района в Клепиковский (312,56 ).

20. Линии по фасовке сметаны могут работать по 20 часов. Перевозка сметаны не предусматривается. Все транспортные затраты возрастают на 50% (330,94 ).

Лабораторная работа №6.
Транспортная задача

Цель работы : овладеть практическими навыками формулирования транспортной задачи и её решения методом потенциалов.

Приборы и материалы : ПЭВМ, оснащённая табличным процессором.

Задание

Составить и решить методом потенциалов задачу в соответствии с нижеследующими условиями и данными индивидуального варианта задания.

Топливно-энергетический комплекс региона включает пять шахт, где добывается бурый уголь, четыре теплоцентрали и две электростанции. Себестоимость добычи 1 т бурого угля на шахтах с первой по пятую составляет соответственно 2,4; 2,8; 3,4; 3,0; 2,9 тыс. руб. Затраты на 1 тонно-километр его перевозки железнодорожным транспортом – 35 руб., автомобильным – 65 руб. Расстояния приведены в табл. 4. Годовой объём добычи угля на каждой шахте и его потребления на теплоцентралях и электростанциях, а также сведения о наличии железнодорожной станции указаны в индивидуальных вариантах задания. Перевозка железнодорожным транспортом возможна только между объектами, расположенными рядом с железнодорожными станциями.

Определить оптимальный план перевозок бурого угля и затраты на обеспечение топливом теплоцентралей и электростанций.

Таблица 4

Расстояния между поставщиками и потребителями бурого угля, км

В случае избытка добывающих мощностей определить также оптимальный план добычи в предположении, что вывоз угля за пределы региона нецелесообразен. В случае недостатка определить, какие теплоцентрали либо электростанции следует обеспечить углём, поставляемым из-за пределов региона по цене 6,2 тыс. руб./т.

Методические указания по выполнению задания

Задание можно выполнять с помощью микрокалькулятора, табличного процессора ПЭВМ или КПК либо самостоятельно разработанной программы, вычисляющей данные, необходимые для составления отчёта. Рекомендуется проверить результаты расчёта с помощью одного из программных средств для решения транспортной задачи, доступных в сети Internet.

Требования к отчёту

В отчёте должны быть представлены:

¨ математическая запись транспортной задачи с указанием названий и единиц измерения переменных и ограничений;

¨ оптимальное решение (значения переменных) и оптимальное значение целевой функции;

¨ доказательство оптимальности полученного решения.

Если иное не предписано преподавателем, отчёт сдаётся в электронном виде на дискете или с помощью средств электронных телекоммуникаций.

Литература

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — раздел 3.2.

Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. – 2-е изд. М.: Финансы и статистика, 2005. — раздел 2.2.6.

Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.

Варианты заданий

Таблица 5

Годовые объёмы добычи и потребления бурого угля, тыс. т.
(символом * отмечены предприятия, не имеющие доступа к железнодорожной станции)

Примечание . Если аудиторное время, выделенное на выполнение лабораторной работы, составляет 4 часа, значения в зачёркнутых клетках используются для формирования индивидуального варианта. Если объём аудиторной работы составляет 2 часа, значения в зачёркнутых клетках при формировании индивидуального варианта задания принимаются равными нулю. Уточните у преподавателя правила формирования варианта индивидуального задания.

Лабораторная работа № 7 .
Динамическое программирование

Цель работы : овладеть практическими навыками формулирования задач поиска оптимального пути, их решения и анализа на основе принципа оптимальности Беллмана.

Приборы и материалы : линейка, карандаш; микрокалькулятор либо КПК, оснащённый табличным процессором.

Задание

1. Составить и решить, используя принцип оптимальности Беллмана, задачу отыскания наиболее дешёвого маршрута доставки груза из пункта A в пункт B при условиях, заданных индивидуальным вариантом задания.

2. Решить задачу при тех же условиях и дополнительном условии обязательного посещения пункта C.

3. Составить и решить, используя принцип оптимальности Беллмана, задачу отыскания минимальной продолжительности выполнения проекта, начинающегося в момент A и завершающегося событием B, при условиях, заданных индивидуальным вариантом задания.

Методические указания по выполнению задания

Задание рекомендуется выполнять, пользуясь графическими изображениями систем допустимых маршрутов и выполняемых работ.

Требования к отчёту

В отчёте должны быть представлены:

¨ граф, отображающий допустимые маршруты, с указанием минимальных затрат на достижение каждого пункта;

¨ оптимальный путь;

¨ минимальные затраты на доставку груза из пункта A в пункт B при условиях заданий 1 и 2;

¨ граф, отображающий последовательность работ, предусмотренную проектом, с указанием ранних сроков наступления каждого события;

¨ критический путь;

¨ минимальный срок выполнения проекта.

Если преподавателем не предписано иначе, отчёт предоставляется в электронном виде на дискете или с использованием средств компьютерных телекоммуникаций.

Литература

Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. – 2-е изд. М.: Финансы и статистика, 2005. — Глава 5.

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — Раздел 3.5.

Варианты заданий

Таблица 6

Исходные данные индивидуальных вариантов заданий
лабораторной работы №7

Лабораторная работа № 8 .
Нелинейное программирование: отражение эффекта масштаба и ценовых эффектов на олигопольных рынках

Цель работы : овладеть практическими навыками решения задач математического программирования градиентными методами с использованием прикладных программ.

Приборы и материалы : ПЭВМ, оснащённая табличным процессором Microsoft Excel с установленной надстройкой «Поиск решения».

Задание

1. Составить и решить задачу математического программирования (с учётом изменений, предусмотренных индивидуальным вариантом задания), предназначенную для составления оптимальной производственной программы ассоциации молокоперерабатывающих предприятий при следующих условиях.

¨ Ассортимент выпускаемой продукции включает пастеризованное молоко, кефир и сметану, а также дополнительную продукцию согласно индивидуальному варианту задания.

¨ Затраты сырого молока при объёме выпуска 100 т в сутки составляют: на пастеризованное молоко – 1,01 кг/кг; на кефир – 1,01 кг/кг; на сметану – 9,45 кг/кг. Затраты сырья зависят от объёмов производства. Эластичность затрат сырья по объёмам продаж постоянна и указана в индивидуальном варианте задания.

¨ Поставщики в состоянии поставить не более 1,4 тыс. т молока в сутки.

¨ Фасовка молока и кефира осуществляется на автоматизированных линиях общей производительностью 50 т молока или 60 т кефира в час. В течение суток оборудование может эксплуатироваться не более 21 часа.

¨ Фасовка сметаны осуществляется на автоматизированных линиях производительностью 3 т сметаны в час. В течение суток линия может эксплуатироваться не более 18 часов.

¨ Оптовая цена продажи при объёме реализации 100 т в сутки: пастеризованного молока – 2,4, кефира – 2,7, сметаны – 13,8 тыс. руб./ц. Цена зависит от объёма продажи. Эластичность цены по объёмам продаж постоянна и указана в индивидуальном варианте задания.

¨ Минимальный суточный объём выпуска продукции каждого вида соответствует количеству, фасуемому на соответствующем оборудовании в течение получаса.

¨ План должен обеспечивать максимальную выручку от реализации молочной продукции (контракт на поставку молока уже оплачен).

2. С помощью составленной задачи определить:

¨ удельные затраты сырого молока на производство каждого вида продукции согласно оптимальному плану;

¨ оптовые цены, соответствующие оптимальному плану;

¨ предельную цену приобретения сырого молока.

3. Оформить отчёт.

Методические указания по выполнению задания

Решать задачу рекомендуется с помощью средства «Поиск решения» табличного процессора Microsoft Excel. Рекомендуемые параметры для процедуры поиска решения: относительная погрешность – 1e-9, допустимое отклонение – 0,005%, сходимость – 1e-9. Переключатели «Неотрицательные переменные» и «Автоматическое масштабирование» включить. Установить: оценки – линейные, разности – прямые, метод поиска – Ньютона.

При аварийной остановке вычислительного процесса, обусловленной присвоением некоторой переменной нулевого или отрицательного значения, следует вручную присвоить данной переменной любое положительное значение, после чего возобновить поиск решения.

При получении сообщения «Решение найдено» следует проконтролировать выполнение ограничений.

Чтобы быть уверенным в обнаружении оптимального решения, необходимо получить не менее трёх его вариантов, пользуясь разными начальными значениями переменных задачи. Если различия между значениями переменных и (или) целевой функции превышают 0.1%, следует повторить решение, уменьшив значения параметров «относительная погрешность» и «сходимость» процедуры поиска решения.

Для ответа на вопросы задания 2 необходимо воспользоваться расчётными формулами, описывающими зависимости цен продукции от объёмов её реализации и потребности в сырье от объёмов выпуска продукции, а также значением множителя Лагранжа по балансу молочного сырья. Значения множителей Лагранжа отображаются в отчёте «Устойчивость». Для создания этого отчёта следует при сохранении найденного оптимального решения в диалоговом окне «Результаты поиска решения» выбрать тип отчёта «Устойчивость».

Требования к отчёту

В отчёте следует привести:

¨ математическую запись задачи математического программирования с указанием названий и единиц измерения переменных и ограничений;

¨ оптимальное решение, оптимальное значение целевой функции и экономическую интерпретацию оптимального плана;

¨ значения множителей Лагранжа, соответствующих ограничениям модели;

¨ обоснованные ответы на вопросы задания 2 с указанием формул, использованных для расчётов.

Если иное не предписано преподавателем, отчёт сдаётся в электронном виде на дискете или с помощью средств электронных телекоммуникаций.

Литература

Шелобаев С.И. Экономико-математические методы и модели: Учеб. пособие для вузов. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — Раздел 4.1.

Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.

Светлов Н.М. , Светлова Г.Н. Построение и решение оптимизационных моделей средствами программ MS Excel и XA / РГАУ – МСХА им. К.А. Тимирязева. М.: 2005.

Варианты заданий

Таблица 7

Исходные данные индивидуальных вариантов заданий
лабораторной работы №8

Лабораторная работа №9.
Оценивание параметров функции Торнквиста

Цель работы : овладеть практическими приёмами эконометрического моделирования в маркетинговых приложениях, усвоить недостатки статистических методов оценивания ненаблюдаемых параметров, выработать критическое отношение к ним, получить представление о величине возможных статистических ошибок при применении распространённых приёмов эконометрического моделирования.

Приборы и материалы : ПЭВМ, оснащённая табличным процессором. Желательно наличие специализированного пакета прикладных программ для статистического анализа (SPSS, Statistica)

Задание

1. Выполнить статистическое оценивание параметра c функции Торнквиста на товары второй необходимости, преобразованной к линейной форме, по имеющимся данным о величинах дохода и спроса на некоторый товар, определив порог возникновения и уровень насыщения спроса на основе имеющихся эмпирических данных (табл. 8).

2. Выполнить статистическое оценивание всех параметров функции Торнквиста методом наименьших квадратов без преобразования её к линейной форме[3] .

3. Сделать заключение о существенности модели (по результатам F-теста) и о существенности отличия от нуля её параметров, оценённых при выполнении двух предыдущих заданий (по результатам t-теста).

4. Определить эластичность спроса по доходу для медианного и максимального уровней дохода в анализируемой совокупности. Расчёты выполнить по результатам оценивания параметров и по данным об их действительных значениях. Сравнить полученные результаты. Дать заключение о степени доверия результатам статистического оценивания.

Методические указания по выполнению задания

Функция Торнквиста для товаров второй необходимости является эмпирической спецификацией теоретической зависимости спроса на продукты от дохода потребителя. Эта спецификация распространяется на продукты, которые не являются жизненно необходимыми, но способны при конечном уровне потребления полностью удовлетворить соответствующую потребность. Она задаётся соотношением где y — спрос на данный товар (кг в год); x — доход (тыс.руб. в год); a — уровень насыщения спроса (кг в год); b —доход, при котором возникает спрос (тыс.руб. в год); c — параметр, определяющий эластичность спроса по доходу при заданных a и b (тыс.руб. в год). Чем больше значение c, тем выше эластичность спроса по доходу.

Чтобы сократить число параметров, оцениваемых статистически, и преодолеть трудности, возникающие при оценивании всех трёх параметров модели (во многих случаях оценки оказываются неустойчивыми), границу возникновения спроса и уровень насыщения часто определяют экзогенно (то есть без обращения к эмпирической модели). При этом ориентируются на минимальный уровень дохода, при котором возникает спрос на данный продукт, и на максимальный уровень спроса на данный продукт, предъявляемый одним потребителем по результатам имеющихся наблюдений.

К заданию 1

Это задание может быть выполнено средствами табличного процессора Microsoft Office Excel.

Граница возникновения спроса может быть определена на основе эмпирических данных. В простейшем случае в качестве этой границы (а значит, величины параметра b) можно принять среднюю арифметическую между максимальным доходом, при котором спрос на исследуемый товар отсутствует, и минимальным доходом, при котором он имеется. При этом не имеет значения, какая из этих двух величин больше.

В качестве уровня насыщения (значения параметра a) рекомендуется принять наибольшее значение спроса среди наблюдаемых.

Зная величины a и b, функцию Торнквиста можно преобразовать к линейной зависимости, связывающей две переменные z и y, причём переменную z можно рассчитать, пользуясь имеющимися данными о спросе и доходе. Умножив левую и правую стороны уравнения на величину x + c, собрав члены, содержащие оцениваемые параметр c, в правой части уравнения и приведя подобные члены, получим простейшее уравнение линейной однофакторной регрессии вида z = cy, где y — спрос (кг в год); z — рассчитываемая на основе эмпирических данных величина a·x – x·y – a·b (тыс.руб./кг)[4] .

Параметр α полученного уравнения может быть оценён с помощью метода наименьших квадратов, что позволяет определить неизвестный параметр c функции Торнквиста для товаров второй необходимости. Но величина z неизбежно, в силу метода её расчёта, распределена асимметрично, что приводит к смещённой оценке параметра α. В процессе оценивания мы увидим, насколько значительным оказывается отклонение оценки параметра от его действительного значения. При использовании процедуры анализа данных «Регрессия» в Microsoft Office Excel следует установить флажок Константа – ноль , обозначающий, что оценивается параметр уравнения вида z = cy, а не z = α + cy.

Действительное значение параметра c в данном случае известно благодаря тому, что совокупности данных, по которым выполняется оценивание, сформированы искусственно. При практических расчётах по оцениванию параметров функции Торнкиста действительные значения никогда не бывают известны.

Для ввода данных о спросе и доходе, приведённых в индивидуальных вариантах задания, целесообразно пользоваться электронным вариантом данного издания, размещённым по адресам http://nsvetlov.narod.ru/umk6/lr-emm.doc и http://svetlov.value.da.ru/lr-emm.doc.

К заданию 2

Это задание требует использования специализированных прикладных программ статистического анализа.

При выполнении второго задания все три параметра функции Торнквиста для товаров второй необходимости оцениваются методом наименьших квадратов с использованием нелинейных процедур отыскания минимума суммы квадратов отклонений воспроизведённых значений спроса от эмпирических.

При использовании программы Statistica 6.0 следует скопировать данные на её рабочий лист, дать команду Statistics ® Advanced Linear/ Nonlinear Models ® Nonlinear Estimation ® Function to be estimated и в появившемся диалоговом окне ввести оцениваемую функцию:

var1=a*(var2-b)/(var2+c)

Нажав псевдокнопку OK , установить в следующем диалоговом окне предельное число итераций метода Левенберга-Марквардта равным 500. Снова нажать OK . В появившемся диалоговом окне Results (последняя строка текстового поля) отображаются значения коэффициента детерминации уравнения связи и коэффициента множественной корреляции. Значения оцениваемых параметров и результаты t-теста можно отобразить, нажав псевдокнопку Summary: Parameter estimates .

При использовании других программных средств необходимые методические указания по их использованию предоставляет преподаватель.

Качество оценивания параметров при данном подходе значительно выше по сравнению с подходом, применённым при выполнении задания 1.

К заданию 3

Заключение о существенности модели и о существенности отличия её параметров от нуля рекомендуется делать, предполагая уровень значимости равным 0,05.

Для модели это заключение делается по результатам F-теста путём сравнения критического (для уровня значимости 0,05) и эмпирического значений величины F отношения воспроизведённой дисперсии эндогенной (зависимой) переменной к остаточной дисперсии.

Для параметров заключение делается по результатам t-теста путём сравнения критического (для уровня значимости 0,05) и эмпирического значений величины t, представляющей собой значение параметра, делённое на его среднюю ошибку.

К заданию 4

Формула для расчёта эластичности спроса по доходу имеет следующий вид:

Требования к отчёту

В отчёте приводятся математические записи функции z = αy и функции Торнквиста в числовой форме с указанием оценённых числовых значений параметров; результаты статистических тестов существенности модели и её параметров для уровня значимости 0,05 с указанием порогового значения уровня значимости, при котором заключение относительно гипотез о существенности модели (параметров) меняется на противоположное; формулы для расчёта эластичностей спроса по доходу с подставленными в них числовыми значениями оценок параметров согласно заданиям 1 и 2, а также действительными значениями параметров; эластичности, рассчитанные по результатам задания 1, задания 2 и по действительным значениям параметров; заключение о достоверности эластичностей, определённых на основе полученных оценок.

Если преподавателем не предписано иначе, отчёт предоставляется в электронном виде на дискете или с использованием средств компьютерных телекоммуникаций.

Литература

Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева . — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — Глава 4.

Эконометрика: начальный курс: Учебник. 8-е издание // Магнус Я.Р., Катышев П.К., Пересецкий А.А. М.: Дело, 2007.

Варианты заданий

Исходные данные для оценивания параметров функции Торнквиста приведены в табл. 8. При этом для формирования задания вариантов 8…14 доход и действительные значения параметров b и c увеличиваются на 20% по сравнению с заданными, а действительные значения параметра a — уменьшаются на 20%. Для формирования вариантов 15…20 доход и действительные значения параметров b и c увеличиваются на 40% по сравнению с заданными, а действительные значения параметра a — уменьшаются на 40%.

Таблица 8

Данные о спросе и доходе

Лабораторная работа №10.
Микроэкономический анализ технологической эффективности фирмы

Цель работы : приобрести навыки оценивания технологической эффективности фирм с помощью метода оболочки данных (DEA).

Приборы и материалы : ПЭВМ, оснащённая табличным процессором; программа линейной оптимизации Sunset XA.

Задание

1. Определить технологическую эффективность консалтинговых фирм, оказывающих услуги по юридическим консультациям и реинжинирингу бизнес-процессов, пользуясь исходными данными об объёме оказываемых ими услуг каждого вида, а также численности юристов и экономистов, приведёнными в индивидуальных вариантах задания.

2. Проверить гипотезу о влиянии размера фирмы на технологическую эффективность.

3. Проверить гипотезу о влиянии доли юристов в штате фирмы на технологическую эффективность.

Методические указания по выполнению задания

Технологическая эффективность должна быть определена для всех фирм совокупности, соответствующей индивидуальному варианту задания.

Если преподавателем не предписано иначе, студенты вправе реализовать любой из известных им вариантов DEA-модели: предусматривающий максимизацию выпуска либо минимизацию расходования ресурсов, с постоянным или переменным эффектом масштаба. Студент должен использовать для выполнения лабораторной работы программное обеспечение линейного программирования. Применение специализированных программных средств, реализующих метод оболочки данных, допускается только в целях проверки полученных результатов и является основанием для повышения рейтинговой оценки выполнения лабораторной работы.

В индивидуальных вариантах заданий переменная y1 соответствует доходу от оказания юридических услуг (тыс. руб.); y2 — доходу от услуг по реинжинирингу (тыс. руб.); x1 — численности юристов в штате фирмы (чел.); x2 — численности экономистов в штате фирмы (чел.).

Для ввода данных о моделируемых фирмах, приведённых в индивидуальных вариантах задания, целесообразно пользоваться электронным вариантом данного издания, размещённым по адресам http://nsvetlov.narod.ru/umk6/lr-emm.doc и http://svetlov.value.da.ru/lr-emm.doc.

Гипотеза о влиянии размера фирмы на технологическую эффективность проверяется путём тестирования значимости ранговой корреляции между общей численностью занятых на фирме (аппроксиматор размера) и технологической эффективностью. Если гипотеза о равенстве коэффициента корреляции по Спирмену нулю не отвергается, нет оснований считать размер фирмы существенным фактором её технологической эффективности. Уровень значимости принять равным 0,05.

Использование коэффициентов корреляции рангов, а не линейной корреляции, обусловлено двумя причинами: во-первых, значения технологической эффективности фирм не подчиняются нормальному закону распределения; во-вторых, связь между размером и технологической эффективностью не обязательно линейная.

Если программное обеспечение, анализирующее корреляцию рангов, не доступно студентам, можно воспользоваться функциями табличного процессора Spearman(вектор1; вектор2), вычисляющей коэффициент корреляции рангов по Спирмену между интервалами ячеек, которым присвоены имена вектор1 и вектор2, и SpearmanP(коэффициент; вектор1), вычисляющей пороговое значение уровня значимости, при котором заключение по гипотезе о равенстве коэффициента корреляции рангов нулю меняется на противоположное. Здесь коэффициент — имя ячейки, содержащей коэффициент ранговой корреляции по Спирмену. Чтобы воспользоваться этими функциями, в Excel 2007 следует дать команду Разработчик ® Visual Basic , открыть окно модуля Module1 (если оно не было открыто ранее) и поместить в это окно программный код, необходимый для работы данных функций, приведённый в приложении к настоящим методическим указаниям[5] . При этом параметры безопасности Excel должны быть настроены таким образом, чтобы обеспечить средний уровень безопасности.

Гипотеза о влиянии доли юристов в штате на технологическую эффективность проверяется путём тестирования значимости ранговой корреляции между долей юристов в штате фирмы и технологической эффективностью. Если гипотеза о равенстве коэффициента корреляции по Спирмену нулю не отвергается, нет оснований считать долю юристов в штате фирмы существенным фактором её технологической эффективности. Уровень значимости принять равным 0,05.

Требования к отчёту

В отчёте приводятся математическая формулировка использованной модели, значения технологической эффективности каждой фирмы, обоснованные расчётами заключения относительно гипотез, проверка которых предусматривается заданиями 1 и 2.

Если преподавателем не предписано иначе, отчёт предоставляется в электронном виде на дискете или с использованием средств компьютерных телекоммуникаций.

Литература

Data envelopment analysis: theory, methodology and application / Edited by A. Charnes . Boston : Kluwer Academic Publishers, 1994.

Светлов Н.М. Альбом наглядных пособий по курсу «Экономико-математическое моделирование». М.: ФГОУ ВПО РГАУ–МСХА имени К.А. Тимирязева, 2009. — Тема 11.

Варианты заданий

Будьте внимательны! Убедитесь, что анализируемый вами ряд данных содержит 25 наблюдений, как предусмотрено заданием.