МИНИСТЕРСТВО ОБЩЕГО
И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РФ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Электротехнический факультет
Кафедра электрических сетей
ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ АКТИВНОЙ МОЩНОСТИ
В ТЕПЛОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЕ
Методические указания
к лабораторной работе
Дисц. « Оптимизация режимов работы энергосистем », спец. 1001, 4 курс д/o
Киров 1999
1 Цель работы
Целью лабораторной работы является овладения навыками расчета опти –
мального распределения активной мощности в теплоэнергетической систе-
ме при различных режимах работы системы: режим учета потерь в линиях,
режим без учета потерь в линии, режим ограничения передаваемой мощь –
ности по линии электропередачи.
2 Программа работы
2.1. Самостоятельно изучить метод Лагранжа и принцип расчета оптималь-
ного распределения активной мощности в теплоэнергетической системе по
этому методу. [1, ]
2.2. Самостоятельно изучить метод штрафных функций и применение его
для решения оптимизационных задач в сетях имеющих ограничение пере –
даваемой мощности.
2.3. Произвести расчет исходных данных необходимых для расчета.
2.4. С помощью программы расчета оптимального распределения активной
мощности произвести расчет для трех заданных режимов работы энерго –
системы.
2.5. По результатам расчетов сделать выводы.
3. Краткие теоретические сведения
3.1. Метод неопределенных множителей Лагранжа.
При решении задач оптимизации режима широко применяется метод не –
определенных множителей Лагранжа, при этом вместо условий экстрему –
ма функции F( х1
, х2
, …. . хn
) связанных между собой уравнениями свя –
зи, находятся условия экстремума функции Лагранжа:
S = F + å li
*Wi
где li
– постоянный множитель при отыскании экстремума функции F
Эти множители называются неопределенными множителями Лагранжа
Приравняв к 0 частные производные от S по всем n переменным, полу –
чим следующую систему уравнений:
¶S/¶Х1
= ¶F/¶Х1
+ å li
*¶W/¶Х1
= 0
¶S/¶Х2
= ¶F/¶Х2
+ å li
*¶W/¶Х2
= 0
¶S/¶Хn
= ¶F/¶Хn
+ å li
*¶W/¶Хn
= 0
Количество уравнений равно количеству неизвестных это дает возмож –
ность найти аргументы соответствующие экстремуму функции F. Чтобы
найденный экстремум действительно имел бы минимум, необходимо про –
верить знак второго дифференциала функции F и S, тоесть если
d2
S > 0
d2
F > 0
то данный экстремум является минимумом.
Оптимальное распределение активной мощности при å РН
= const
DРН
= const
Обозначим через Т минимум капитальных затрат. Искомыми являются значения активных мощностей отдельных электростанций: Р1
, Р2
, Р3
….. Рn
где n – количество электростанций, где затраты зависят только от выработ-
ки активной мощности. Считаем что все электростанции являются тепло –
выми. Уравнение связи:
W = Р1
+ Р2
+ Р3
+……+ Рn
При этом функция Логранжа запишеться следующим образом:
S = Т - å li
*W
Условию экстремума соответствует равенство нулю частных производных по всем n переменным:
¶S/¶Р1
= ¶Т/¶Р1
+ l *¶W/¶Р1
= ¶Т/¶Р1
+ l = 0
¶S/¶Р2
= ¶Т/¶Р2
+ l *¶W/¶Р2
= ¶Т/¶Р2
+ l = 0
¶S/¶Рn
= ¶Т/¶Рn
+ l *¶W/¶Рn
= ¶Т/¶Рn
+ l = 0
Из этого выражения видно, что
- l = ¶Т/¶Р1
= ¶Т/¶Р2
=……. = ¶Т/¶Рn
Виду того, что Т = Т1
+ Т2
+ ……. + Тn
(затраты равны сумме по всем электрическим станциям)
это выражение можно записать следующим образом:
¶Т1
/¶Р1
= ¶Т2
/¶Р2
=……. = ¶Тn
/¶Рn
Частная производная от затрат на каком либо агрегате или электростанции по активной мощности агрегата или электростанции называется удельным
приростом затрат агрегата или электростанции и обозначается e
e = ¶Тi
/¶Рi
удельный прирост затрат зависит от величины активной мощности. В этом
случае условие оптимального распределения мощности между электростанциями
d2
S = d2
Т + l*d2
W
d2
Т = ¶Т1
/¶Р1
2
*(dР1
2
) + ¶2
Т2
/¶Р2
2
*(dР2
) + ………. + 2*¶2
Т1
/(¶Р1
*¶Р2
)*(dР1
*dР2
) +
+ 2*¶2
Т2
/(¶Р2
*¶Р3
)*(dР2
*dР3
) + ………
смешанные частные производные всегда будут равны нулю так как удель –
ный прирост одного агрегата не зависит от мощности второго агрегата, тогда
d2
Т = ¶Т1
/¶Р1
2
*(dР1
2
) + ¶2
Т2
/¶Р2
2
*(dР2
) + ……….
d2
W = ¶W/¶Р1
2
*(dР1
2
) + ¶2
W/¶Р2
2
*(dР2
) + …..…. + 2*¶2
W/(¶Р1
*¶Р2
)*(dР1
*dР2
) +
+ 2*¶2
W/(¶Р2
*¶Р3
)*(dР2
*dР3
) + ………
В этом случае смешанные частные производные также будут равны нулю,
ввиду того, что
¶W/¶Р1
= 1 , ¶W/¶Р2
= 1 …….
тогда ¶2
W/¶2
Р1
= 0 , ¶2
W/¶2
Р2
= 0 ……… следовательно d2
W = 0
тогда условие d2
S > 0 имеет место если
   ¶2
Т1
/¶Р1
2
> 0 ¶2
Т2
/¶Р2
2
> 0 ………. ¶2
Тn
/¶Рn
2
> 0 ¶2
Т1
/¶Р1
2
> 0 ¶2
Т2
/¶Р2
2
> 0 ………. ¶2
Тn
/¶Рn
2
> 0
таким образом если из неубывающих кривых e1
= e2
=……… = en
хотябы
 одна является возрастающей, то условие d2
S > 0 имеет место, тоесть это одна является возрастающей, то условие d2
S > 0 имеет место, тоесть это
означает что удельные приросты не снижаются при росте активной мощ –
ности а хотя бы у одного из агрегатов возрастают.
Пусть суммарные потери активной мощности в сетях зависят только от ве–
личины активных мощностей электростанций.
DР = f ( P1
, P2
…….. Pn
), тогда условия оптимального распределения мощ –
ности можно записать следующим образом:
 ¶S/¶Р1
= ¶Т/¶Р1
+ l *¶W/¶Р1
= e1
+ l*( 1- ¶DР/¶Р1
) = 0 ¶S/¶Р1
= ¶Т/¶Р1
+ l *¶W/¶Р1
= e1
+ l*( 1- ¶DР/¶Р1
) = 0
¶S/¶Р2
= ¶Т/¶Р2
+ l *¶W/¶Р2
= e2
+ l*( 1- ¶DР/¶Р2
) = 0
¶S/¶Рn
= ¶Т/¶Рn
+ l *¶W/¶Рn
= en
+ l*( 1- ¶DР/¶Рn
) = 0
откуда m = - l = e1
/( 1 - ¶DР/¶Р1
) = e2
/( 1 - ¶DР/¶Р2
)
величина m называется удельным приростом энергосистемы при учете по –
терь в сетях, а величина ei
/( 1 - ¶DР/¶Рi
) называется удельным приростом
i – ой электростанции с учетом потерь в сетях.
3.1. Метод штрафных функций.
Ограничения накладываемые на искомые переменные могут учитываться с
помощью так называемых штрафных функций. Этот прием основывается
на добавление к минимизируемой функции некоторой дополнительной ( штрафной ) достаточно большой по величине за пределами допустимого изменения переменного и равной нулю в диапазоне от Хj min
до Хj mах
/рис.1/
Рисунок 1 Штрафная функция.
Штрафная функция не должна вносить посторонних решений, то есть при-
водить к появлению дополнительных локальных экстремумов минимизи –
руемой функции в области допустимых режимов. Последнее определяет
то, что в этой области штрафная функция должна быть вогнутой.
Шj
= К1
/2*( Хj
- Хj min
)2
при Хj
< Хj min
  Шj
= 0 при Хj min
< Хj
< Хj mах Шj
= 0 при Хj min
< Хj
< Хj mах
Шj
= К2
/2*( Хj
- Хj mах
)2
при Хj
> Хj mах
где К1
, К2
– постоянные коэффициенты (коэффициенты штрафа)
Производная штрафной функции имеет вид:
Шj
= К2
*( Хj
- Хj mах
) при Хj
> Хj mах
Штрафные функции учитывающие ограничения накладываемые на пере –
менные используются для решения задач оптимизации режима методом
Лагранжа и градиентным методом. Если, например, распределяется актив-
ная мощность в теплоэнергетической системе по методу Лагранжа при
заданном ограничении по пропускной способности некоторой линии L
 где РL
< PL max
то штрафная функция запишется: где РL
< PL max
то штрафная функция запишется:
Ш = К/2*( РL
– PL mах
)2
Рассмотрим применение штрафной функции с помощью методу Лагранжа
функция Лагранжа будет иметь следующий вид:
S = Т + l*W + К/2*( РL
– PL mах
)2
В этом случае условие оптимального распределения мощности сводится к отысканию частных производных:
 ¶S/¶Р1
= e1
+ l*( 1- ¶DР/¶Р1
) + К*( РL
– PL mах
) *¶( РL
– PL mах
)/¶Р1
= 0 ¶S/¶Р1
= e1
+ l*( 1- ¶DР/¶Р1
) + К*( РL
– PL mах
) *¶( РL
– PL mах
)/¶Р1
= 0
¶S/¶Р2
= e2
+ l*( 1- ¶DР/¶Р2
) + К*( РL
– PL mах
) *¶( РL
– PL mах
)/¶Р2
= 0
¶S/¶Рn
= en
+ l*( 1- ¶DР/¶Рn
) + К*( РL
– PL mах
) *¶( РL
– PL mах
)/¶Рn
= 0
Активная мощность, протекающая по линии L может быть представлена
как линейная комбинация узловых мощностей. Таким образом, оптималь –
ное распределение мощности с учетом штрафных функций определятся
следующим выражением:
 m = e1
+ К*а1L
*( РL
– PL mах
) = e2
+ К*а2L
*( РL
– PL mах
) m = e1
+ К*а1L
*( РL
– PL mах
) = e2
+ К*а2L
*( РL
– PL mах
)
 1 - ¶DР/¶Р1
1 - ¶DР/¶Р1 1 - ¶DР/¶Р1
1 - ¶DР/¶Р1
где а1L
= ¶( РL
– PL mах
)/¶Р1
, а2L
= ¶( РL
– PL mах
)/¶Р2
4. Общие сведения о рассматриваемой оптимизационной задаче.
Рассмотрим схему содержащую две ТЭЦ ЭС2 и ЭС3 питающие по ЛЭП
110 кВ нагрузку 70 МВт /рис. 2/. Необходимо распределить суммарную
нагрузку системы между двумя станциями если известны удельные при-
росты /табл. 1/. Расчеты произвести с точностью небаланса мощности
DР = 0,3 МВт. Рисунок 2. Рассматриваемая схема теплоэнергетической сети
Таблица 1. Удельные приросты электростанций В данном случае критерий оптимального распределения запишеться следующим образом: mс
= e2
/( 1 - ¶DР/¶Р2
) = e3
/( 1 - ¶DР/¶Р3
)
Примем за балансирующий и базисный узел N 3. При этом мощность Р3
исключается из числа независимых переменных и критерии оптимально–
го распределения принимают следующий вид:
DР = åi
åj
Bj
*Рi
*Pj
при определении потерь в линиях предпологаем что напряжение в узлах
равно номинальному и что потери зависят только от активной мощности
В этом случае потери и удельные приросты потерь записываются следу –
ющим образом:
¶DР/¶Рi
= 2*åj
Bij
*Рj
,
где Bij
= 1/Rij
DР = B11
*P1
2
+ B22
*P2
2
+ 2*P1
*P2
*B12
¶DР/¶Р2
= 2*B12
*P1
+ 2*B22
*P2
B11
= r 11
/ U2
B12
= r 12
/ U2
B22
= r 22
/ U2
Искомое оптимальное распределение между станциями будем определять
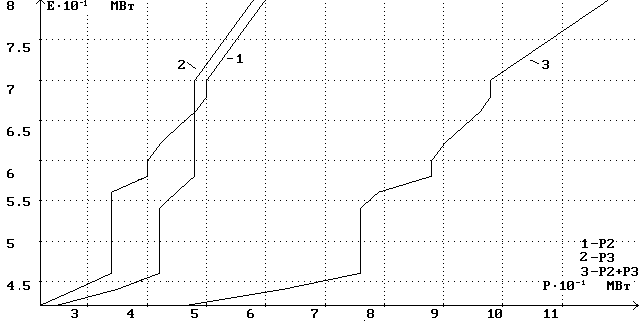
интерактивным путем. В качестве начального приближения используем режим без учета потерь в линии. Для этой цели построим графики удель-ных электроприростов станций /рис. 3/ по данным таблицы 1
 Дальнейший расчет производиться по программе « optimum ». Дальнейший расчет производиться по программе « optimum ».
 Рисунок 3. удельные графики электроприростов станций Рисунок 3. удельные графики электроприростов станций
5. Порядок выполнения лабораторной работы
ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА:
ИЗ ТАБЛИЦЫ ИСХОДНЫХ ДАННЫХ ДЛЯ СВОЕГО ВАРИАНТА ВЗЯТЬ СЛЕДУЮЩИЕ ПАРАМЕТРЫ: Р1, Р2, R12, R13, НАПРЯЖЕНИЕ СЕТИ U=110 кВ
ТОЧНОСТЬ НЕБАЛАНСА МОЩНОСТИ DP= 0,3 МВт
СХЕМА СЕТИ ВЫВОДИТСЯ НА ЭКРАН ПРИ РАБОТЕ С ПРОГРАММОЙ
П.1
.
РАСЧЕТ ПАРАМЕТРОВ ДЛЯ ВВОДА В ПРОГРАММУ
r 11 = R13
r 12 = R13
r 22 = R12 + R13
B11 = r 11 / U2
B12 = r 12 / U2
B13 = r 22 / U2
ИЗ ГРАФИКОВ УДЕЛЬНЫХ ПРИРОСТОВ СНЯТЬ ЗНАЧЕНИЯ Е2 И Е3 ПРИ Р= Р1+ Р2
С КРИВОЙ 3
ИЗ ГРАФИКОВ УДЕЛЬНЫХ ПРИРОСТОВ СНЯТЬ ЗНАЧЕНИЯ Р20 И Р30 СООТВЕТСТВУЮЩИЕ Е2 И Е3 СООТВЕТСТВЕННО С КРИВЫХ 1 И 2
ПРИНЯТЬ MC = E3
ПОТЕРИ МОЩНОСТИ DP = B11*( - P1 )2
+ B22*( P20 - P2 )2
+ 2*B12*( - P1 )*( P20 - P2 )
НЕБАЛАНС МОЩНОСТИ dP = P20 + P30 - P1 - P2 - DP
П.2
ВЫПОЛНИТЬ РАСЧЕТ ОПТИМАЛЬНОГО РЕЖИМА РАСПРЕДЕЛЕНИЯ МОЩНОСТИ В ТЕПЛОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЕ С УЧЕТОМ ПОТЕРЬ АКТИВНОЙ МОЩНОСТИ
ПО ПРОГРАММЕ СЛЕДУЮЩИМ ОБРАЗОМ:
В МЕНЮ ПРОГРАММЫ ВЫБИРАЕТСЯ ПУНКТ "С УЧЕТОМ ПОТЕРЬ "
ВВЕСТИ ИСХОДНЫЕ ДАННЫЕ
ВВЕСТИ ЗНАЧЕНИЯ ТАБЛИЦЫ УДЕЛЬНЫХ ПРИРОСТОВ
ВВЕСТИ ЗНАЧЕНИЯ РУЧНОГО РАСЧЕТА П.1
СЛЕДУЙТЕ УКАЗАНИЯМ, ВЫВОДИМЫМ НА ЭКРАН
ВАМ НУЖНО ДОБИТЬСЯ СНИЖЕНИЯ МОЩНОСТИ НЕБАЛАНСА ПО МОДУЛЮ ДО ЗНАЧЕНИЯ МЕНЬШЕГО НЕБАЛАНСА МОЩНОСТИ dP= 0,3 MBт МЕТОДОМ ПОДБОРА МС
. ДЛЯ ЭТОГО, ПО ЗАПРОСУ ПРОГРАММЫ ВВОДИТЕ ЗНАЧЕНИЯ МС
И СМОТРИТЕ
ПО РЕЗУЛЬТАТАМ РАСЧЕТА КАК ИЗМЕНЯЕТЬСЯ МОЩНОСТЬ НЕБАЛАНСА
ВАМ НУЖНО ПОДОБРАТЬ ТАКОЕ ЗНАЧЕНИЕ МС
ЧТО БЫ МОЩНОСТЬ НЕБАЛАНСА
НЕ ПРЕВЫШАЛА ПО МОДУЛЮ 0,3 МВт
РАСЧЕТ ПО ПРОГРАММЕ ЗАКАНЧИВАЕТСЯ ПО ДОСТИЖЕНИИ МОЩНОСТИ НЕБАЛАНСА ПО МОДУЛЮ < dP
СПИСАТЬ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
ПОСЛЕ ПРОСМОТРА ГРАФИКОВ НАЖМИТЕ "Esc"
П.3
ПОВТОРИТЬ П.2 ,ВЫБРАВ В МЕНЮ ПРОГРАММЫ ПУНКТ "БЕЗ УЧЕТА ПОТЕРЬ
"
П.4
ВЫПОЛНИТЬ РАСЧЕТ ОПТИМАЛЬНОГО РЕЖИМА РАСПРЕДЕЛЕНИЯ МОЩНОСТИ В ТЕПЛОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЕ С УЧЕТОМ ПОТЕРЬ АКТИВНОЙ МОЩНОСТИ И УЧЕТОМ ОГРАНИЧЕНИЯ ПЕРЕДАВАЕМОЙ
МАКСИМАЛЬНОЙ МОЩНОСТИ ПО ЛИНИИ 1-2
ПОРЯДОК ДЕЙСТВИЙ:
В МЕНЮ ПРОГРАММЫ ВЫБРАТЬ ПУНКТ "С УЧЕТОМ ОГРАНИЧЕНИЯ ПЕРЕДАВАЕМОЙ МОЩНОСТИ"
ВВЕСТИ ПАРАМЕТРЫ РАСЧИТАННЫЕ В П.1
ИЗ ТАБЛИЦЫ ИСХОДНЫХ ДАННЫХ ДЛЯ СВОЕГО ВАРИАНТА ВЗЯТЬ Рмах
СПИСАТЬ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ РАСЧЕТА
ПОВТОРИТЬ РАСЧЕТЫ П.4, ИЗМЕНЯЯ Рмах В ПЕДЕЛАХ УКАЗАННЫХ В ТАБЛИЦЕ ИСХОДНЫХ ДАННЫХ ДЛЯ СВОЕГО ВАРИАНТА С ШАГОМ 1 МВт
ПОСТРОИТЬ ЗАВИСИМОСТЬ Рмах ОТ Кшт
6. Требования к отчету
Отчет по лабораторной работе должен содержать:
1) титульный лист
2) цель работы
3) схему рассматриваемой теплоэнергетической системы
4) исходные данные для расчета начальных значений параметров оптимизации
5) расчета начальных значений параметров оптимизации
6) таблицу удельных приростов электростанций
7) график, построенный по данным таблицы удельных приростов электростанций
8) результаты расчета трех оптимизационных режимов в виде таблиц
9) график зависимости kш
от Рмах
по результатам расчета третьего оптимизационного режима
7. Контрольные вопросы
1 Сущность метода неопределенных множителей Лагранжа для расчета
оптимизационных режимов энергосистем.
2 Что представляют собой постоянные множители Лагранжа при отыска –
нии экстремума функции ?
3 Как выглядит уравнение связи при n отдельных электростанциях и
å РН
= const DРН
= const ?
4 Что называется удельным приростом затрат агрегата и от чего в данном
случае он зависит ?
5 Как выглядит критерий оптимального распределения в теплоэнерге -
тической сети по методу неопределенных множителей Лагранжа и что в
него входит?
6 Сущность метода штрафных функций при расчете режимов ограниче -ния передаваемой мощности
7 Что такое коэффициент штрафа и от чего он зависит ?
8 Требования, предъявляемые к штрафным функциям
9 Какие ограничения учитываются штрафными функциями ?
10 Как выглядит критерий оптимального распределения мощности с учетом штрафных функций и что в него входит ?
8. Литература
1. Горнштейн В. М. « Методы оптимизации режимов энергосистем » - М
Энергия 1981г
2. Холмский В. Г. « расчет и оптимизация режимов электрических сетей » - М Высшая школа 1975г
|