| Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет
АРХИТЕКТУРА ЭВМ И ВС
Методические указания к лабораторным работам
для студентов 1-го курса ФПМИ
Составители:
Доцент кафедры ПВТ к.т.н. Маркова В.П.
Ассистент кафедры ПВТ к.ф.-м.н. Куликов И.М.
Новосибирск 2011
Введение
Целями лабораторных работ являются приобретение практических знаний по:
- идентификации оборудования и программного окружения ЭВМ,
- представлению вещественных чисел в ЭВМ,
- сравнению различных способов обхода памяти,
- программному определению размера и степени ассоциативности кэш-памяти различных уровней,
- использованию SIMD-расширения архитектуры x86,
- использованию интерфейса OpenMP для программирования простых многопоточных приложений.
Порядок выполнения работ
Лабораторные работы 1, 2 и 3 являются обязательными для выполнения, лабораторная работа 4 является дополнительной. За лабораторные работы 1 и 2 выставляются максимум по 10 баллов, за лабораторную работу 3 выставляется максимум 20 баллов, лабораторная работа 4 оценивается максимум 40 баллов. Количество баллов, полученных за выполнение каждой из лабораторных работ, определяется по выполненным заданиям к лабораторной работе в соответствии с баллом такого задания и сроком сдачи. В случае сдачи лабораторной работы после крайней даты сдачи дополнительные задания не засчитываются и соответствующие баллы за них не выставляются. Базовые задания первых трёх лабораторных работ должны быть выполнены обязательно, без них лабораторная работа считается не сданной.
Отчёт по лабораторной работе нужно подготавливать в электронном виде и высылать на e-mail преподавателя [email protected], по результатам сдачи отчёта студент при необходимости приглашается на защиту. В отчёт необходимо включить титульный лист; список выполненных заданий по лабораторной работе; текст программы; необходимые тесты, графики зависимостей, результаты замера времени и т. п.; выводы, сделанные на основании выполнения лабораторной работы.
Студенты, сдавшие четыре лабораторные работы и получившие в сумме максимальный балл (80 баллов
) претендуют на получение зачёта «автоматом» с максимальным баллом по предмету (100 баллов
). Для допуска к зачёту необходимо набрать 31 балл
за лабораторные работы.
Лабораторная работа № 1
Представление чисел и определения типа оборудования
Цель работы.
Идентификация оборудования и программного окружения ЭВМ, изучение представления вещественных чисел в ЭВМ.
Методические указания.
1. Представление беззнаковых целых чисел
Для представления беззнаковых целых чисел необходимо перевести из десятичной системы исчисления в двоичную. Например, число 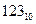 можно представить в виде суперпозиции по степеням двойки: можно представить в виде суперпозиции по степеням двойки:
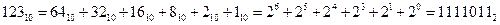 , ,
где единицы в двоичном представлении числа стоят на позиции соответствующих степеней двоек. Для простоты рассмотрим беззнаковый однобайтовый тип данных (тип unsigned
char
в языках С/С++). Для записи числа 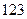 в такой тип данных необходимо дополнить двоичное представление до 8 знаков в такой тип данных необходимо дополнить двоичное представление до 8 знаков 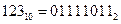 и записать полученные значения в соответствующие биты: и записать полученные значения в соответствующие биты:
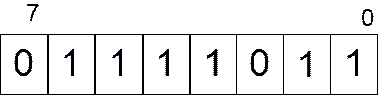
Рисунок 1.
2. Представление знаковых целых чисел
В случае знаковых типов данных старший бит отвечает за знак числа (1 – отрицательное число, 0 – положительное число). Основной проблемой является представление отрицательных чисел. Для такого представления существует следующий алгоритм:
1. нахождение двоичного представления модуля числа,
2. нахождение двоичного дополнения числа,
3. прибавление единицы.
Рассмотрим алгоритм на примере. Представим число 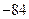 в знаковом однобайтном типе данных (тип char
в языках С/С++): в знаковом однобайтном типе данных (тип char
в языках С/С++):
1. Двоичное представление 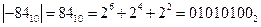 , ,
2. Для нахождения двоичного представления инвертируем все биты числа 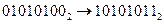 , ,
3. Прибавляем единицу 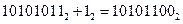 . .
После этого записываем полученные значения в соответствующие биты:
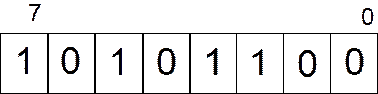
Рисунок 2.
3. Представление вещественных чисел
Основной интерес в вычислениях представляют вещественные типы данных и погрешности округления, связанные с ними. По стандарту IEEE 754 вещественное число 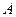 представляется в виде: представляется в виде:
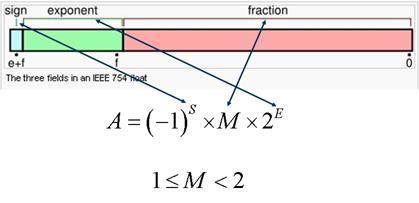
Рисунок 3.
Где  – однобитовый знак числа, – однобитовый знак числа, 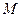 – нормализованная мантисса, – нормализованная мантисса, 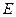 – показатель степени двойки. В случае типа float
под мантиссу выделяется 23 бита, экспоненту 8 бит, в случае типа double
52 бита, экспоненту 11 бит. – показатель степени двойки. В случае типа float
под мантиссу выделяется 23 бита, экспоненту 8 бит, в случае типа double
52 бита, экспоненту 11 бит.
Приведём пример представления вещественного числа 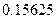 в типе float
. Основной задачей является запись числа в виде в типе float
. Основной задачей является запись числа в виде 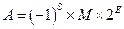 . Число можно записать в виде . Число можно записать в виде 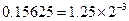 , в данном случае мантисса имеет вид , в данном случае мантисса имеет вид 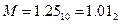 нормализация мантиссы позволяет отбросить единицу и записывать только дробную часть. Таким образом нормализация мантиссы позволяет отбросить единицу и записывать только дробную часть. Таким образом 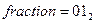 . Далее записываем показатель степени двойки. При этом нужно учитывать, что эта степень может быть как отрицательной так и положительной. Для этого показатель степени имеет вид: . Далее записываем показатель степени двойки. При этом нужно учитывать, что эта степень может быть как отрицательной так и положительной. Для этого показатель степени имеет вид:
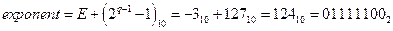 , ,
где 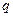 – количество бит на показатель степени двойки. В результате число – количество бит на показатель степени двойки. В результате число 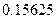 представимо в виде: представимо в виде:

Рисунок 4.
В завершении описания представления вещественных чисел нужно отметить, что для стандартных типов данных (float
и double
) имеют место следующие значения:
Таблица 1.
| Тип
|
Минимальный порядок*
|
Максимальный порядок
|
Число значащих знаков
|
| float
|
– 45
|
38
|
7
|
| double
|
– 323
|
308
|
15
|
(*) Стоит отметить, что мантисса может быть ненормализованной, что и приводит к таким значениям минимального порядка.
4. Идентификация оборудования и программного окружения
Средствами операционной системы Windows можно узнать достаточно много информации об оборудовании, памяти (функция GlobalMemoryStatus
), жёстких дисках (функция GetDiskFreeSpace
), сети и мониторе (функция GetSystemMetrics
при различных параметрах), программном окружении (функции GetComputerName
и GetUserName
) и о многом другом. Подробное описание функций и примеры их использования можно найти в справочной системе MSDN.
Для определения таких параметров процессора, как фирма производитель, наличие расширений, количества и параметров кэшей команд и данных, TLB и других параметров в случае архитектур x86 используется инструкция процессора cpuid
, которая имеет интерфейс на языке С/С++ __cpuid
. Так для определения идентификатора процессора имеет место следующий код:
#include <intrin.h> // подключение описания функции __cpuid
…
int CPUInfo[4];
char CPUString[32];
__cpuid(CPUInfo, 0);
memset(CPUString, 0, sizeof(CPUString));
*((int*)CPUString) = CPUInfo[1];
*((int*)(CPUString+4)) = CPUInfo[3];
*((int*)(CPUString+8)) = CPUInfo[2];
printf(" CPU vendor: %s\n",CPUString);
…
Первый параметр функции __cpuid
– 4-х элементный целочисленный массив, который соответствует регистрам eax, ebx, ecx, edx после выполнения инструкции. Второй параметр функции – номер функции инструкции. Подробная информация о номерах функций инструкции cpuid
и содержимом регистров приведена в документах [1,2] для процессоров Intel и AMD. Так например с помощью функций 0x80000002, 0x80000003, 0x80000004 можно узнать полное название процессора.
Задание.
1. В соответствии с вариантом задания записать представление целого числа в типе char
и вещественного числа в типе float
(Обязательное задание
– 5 баллов).
2. С помощью функций WinAPI определить информацию об оперативной памяти (Дополнительное задание
– 1 балл).
3. С помощью функций WinAPI определить информацию о памяти на одном из жёстких дисков (Дополнительное задание
– 2 балла).
4. С помощью инструкции cpuid определить название процессора (Дополнительное задание
– 2 балла).
5. Крайний срок сдачи – 1 апреля 2011 года
.
Варианты.
1. Целое число –12, вещественное число 12.5.
2. Целое число –23, вещественное число 12.125.
3. Целое число –56, вещественное число 12.25.
4. Целое число –78, вещественное число 12.75.
5. Целое число –89, вещественное число 12.625.
6. Целое число –90, вещественное число 24.5.
7. Целое число –21, вещественное число 24.125.
8. Целое число –45, вещественное число 24.25.
9. Целое число –78, вещественное число 24.75.
10. Целое число –86, вещественное число 24.625.
Лабораторная работа № 2
Исследование кэш-памяти и обхода памяти
Цель работы.
Сравнение различных способов обхода памяти, программное определение размера и степени ассоциативности кэш-памяти различных уровней.
Методические указания.
1. Кэш-память
Кэш-память является промежуточным хранилищем данных между процессором и оперативной памятью. Она содержит копии наиболее часто используемых блоков данных из оперативной памяти. Размер кэш-памяти составляет от нескольких килобайт до нескольких мегабайт, а скорость доступа к ней в несколько раз превосходит скорость доступа к оперативной памяти, но уступает скорости обращения к регистрам. Каждый раз, когда к ячейке оперативной памяти происходит обращение (чтение или запись), ее копия заносится в кэш-память, вытеснив при этом оттуда копию другой ячейки. Поэтому повторное обращение к той же ячейке произойдет быстрее. Значения переменных программы и небольшие массивы, для которых не нашлось места в регистрах, обычно располагаются в кэш-памяти. Большие массивы могут поместиться в кэш-память только частично. Допустим, некоторая программа производит многократную обработку элементов массива. Если построить график зависимости времени обработки массива от размера массива, то он должен иметь нелинейный характер. При превышении размера кэш-памяти время обращения к элементам массива несколько возрастет (на графике будет наблюдаться скачок). Данные из оперативной памяти в кэш-память (и обратно) считываются целыми строками. Размер кэш-строки в большинстве распространенных процессоров составляет 16, 32, 64, 128 байт. При последовательном обходе попытка чтения первого элемента кэш-строки вызывает копирование всей строки из медленной оперативной памяти в кэш. Чтение нескольких последующих элементов выполняется намного быстрее, т.к. они уже находятся в быстрой кэш-памяти. В большинстве современных микропроцессорах реализована аппаратная предвыборка данных. Ее суть состоит в том, что при последовательном обходе очередные кэш-строки копируются из оперативной памяти в кэш-память еще до того, как к ним произошло обращение. За счет этого скорость последовательного обхода данных еще возрастает.
Большинство современных микропроцессоров имеют множественно-ассоциативную (наборно-ассоциативную) организацию кэш-памяти. При множественно-ассоциативной организации кэш-память разделена на несколько банков, и каждый блок данных из оперативной памяти может быть помещен в одну из определенного множества (набора) строк кэш-памяти. Число строк в множестве определяется числом банков. Схема кэш-памяти данных первого уровня на Pentium III (16 Кб):
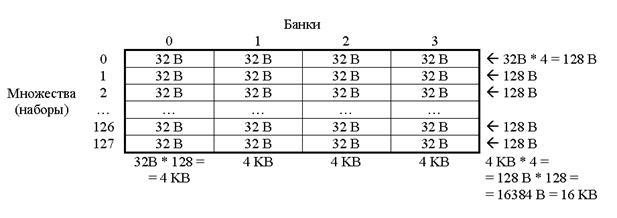
Рисунок 5.
В какой конкретный элемент множества строка будет записана, определяется алгоритмом замещения (циклический, случайный, LRU, псевдо-LRU, …). Таким образом, блоки, отстоящие на определенное расстояние в памяти (в примере: на 212
B = 4096 B = 4 KB), помещаются в одно и то же множество строк. Число элементов в каждом множестве (число банков) называется степенью ассоциативности
кэш-памяти. Например, кэш данных L1 в Pentium III имеет объем 16 KB, степень ассоциативности 4 (4-way set-associative), размер строки 32B:
16KB = 4-way * 4 KB = 4-way * 128 множеств * 32B
Данные, расположенные в памяти с шагом на расстоянии 4KB приходятся на одно множество. На все эти данные приходится всего 4 кэш-строки, т.е. 4 * 32 = 128 B. Если выполнять обход данных с шагом 4 KB, то из всех 16 KB кэша L1 будет использоваться всего 128 B, которые будут постоянно перезаписываться (эффект «буксования» кэша). Производительность при этом будет такая же, как при отсутствии кэш-памяти. Если вычислительная система имеет несколько уровней кэш-памяти, то у каждого уровня может быть своя степень ассоциативности. Определить степени ассоциативности кэш-памяти можно следующим способом. Выполняется обход N блоков данных суммарным объемом BlockSize, отстоящих друг от друга на величину Offset:
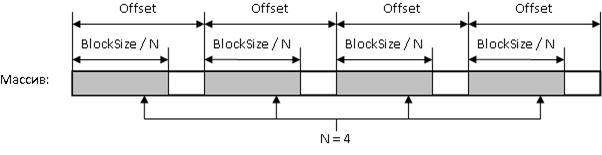
Рисунок 6.
BlockSize должен быть не больше объема исследуемого уровня кэш-памяти. Offset должно быть кратно величине «размер кэша» / «ассоциативность», т.е. кратно размеру банка ассоциативности. Как правило, это степени двоек, так что можно взять заведомо кратное такому значению расстояние (например, 1MB). Изменяя число частей N, мы увидим, как меняется время обхода. Когда N превысит число банков, время обхода сильно возрастет.
Обход элементов следует производить в таком порядке:
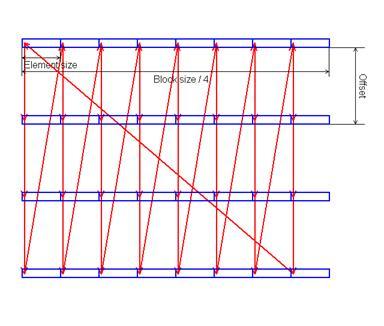
Рисунок 7.
2. Функции замера времени
Для замера времени небольших операций (несколько сотен инструкций) используется инструкция процессора rdtsc
, которая лежит в основе функций WinAPI QueryPerformanceFrequency
и QueryPerformanceCounter
. Пример использования этих функций приведён ниже:
#include <stdio.h>
#include <windows.h>
int main()
{
LARGE_INTEGER b_start,b_stop,b_time,freq;
double time, pi;
QueryPerformanceFrequency(&freq);
QueryPerformanceCounter(&b_start);
pi = pi_calculate();
QueryPerformanceCounter(&b_stop);
b_time.QuadPart = b_stop.QuadPart - b_start.QuadPart;
printf("Time: %lf sec Pi = %lf\n",
(double)(b_time.QuadPart)/(double)(freq.QuadPart) ,pi);
return 0;
}
3. Процедура умножения матриц
Самым быстрым способом обхода является прямой последовательный. Это значит, что после обращения в программе к некоторому элементу происходит обращение к элементу, следующему в памяти прямо за ним. Рассмотрим размещение в памяти двумерного массива в программе на языке Си.
float A[N][N];
Известно, что в языке Си массивы располагаются в памяти по строкам (сначала идут элементы первой строки, затем элементы второй строки и т.д.). Значит, в памяти он разместится следующим образом:
| …
|
A0,0
|
A0,1
|
A0,2
|
…
|
A0,N-1
|
A1,0
|
A1,1
|
A1,2
|
…
|
A1,N-1
|
…
|
AN-1,0
|
AN-1,1
|
AN-1,2
|
…
|
AN
-1,
N
-1
|
…
|
Получается два варианта перебора элементов массива:
| Быстро
:
for
(i=0;i<N;i++)
for
(j=0;j<N;j++) A[i][j]=x;
|
Медленно:
for
(j=0;j<N;j++)
for
(i=0;i<N;i++) A[i][j]=x;
|
Рассмотрим задачу перемножения двух квадратных матриц N×N. Если напрямую запрограммировать известную формулу: 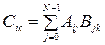 , например, на языке Си, получим следующий фрагмент программы: , например, на языке Си, получим следующий фрагмент программы:
for (i=0;i<N;i++)
for (k=0;k<N;k++)
for (j=0;j<N;j++) C[i][k]+=A[i][j]*B[j][k];
Заметим, что в этом случае массив A перебирается по строкам, а массив B – по столбцам (смотрим на внутренний цикл). Зная, что массивы в языке Си хранятся по строкам, приходим к выводу, что элементы массива A перебираются последовательно, а элементы массива B – нет. В данном случае порядок обхода массива C практически не важен, поскольку между обращениями к различным его элементам проходит довольно много времени. Чтобы ускорить программу, нужно, чтобы, по крайней мере, во внутреннем цикле элементы массивов перебирались последовательно. Для этого необходимо либо заранее транспонировать массив B, либо переставить циклы следующим образом:
for (i=0;i<N;i++)
for (j=0;j<N;j++)
for (k=0;k<N;k++) C[i][k]+=A[i][j]*B[j][k];
Задание
.
1. Реализовать прямой обход памяти (Обязательное задание
– 1 балла).
2. Реализовать обратный обход памяти (Обязательное задание
– 1 балла).
3. Реализовать случайный обход памяти (Обязательное задание
– 1 балла).
4. Определить степень ассоциативности кэш-памяти (Обязательное задание
– 2 балла).
5. Сравнить умножение двух квадратных матриц с использованием стандартного алгоритма и алгоритма с учётом прямого обхода памяти (Дополнительное задание
– 5 баллов).
6. Крайний срок сдачи – 15 апреля 2011 года
.
Лабораторная работа № 3
Использование SIMD-расширений архитектуры x86
Цель работы.
Научиться использовать SIMD-расширения архитектуры x86 в программах на языках С/С++.
Методические указания.
1.
SIMD
-расширения архитектуры
x
86
SIMD-расширения (Single Instruction Multiple Data) были введены в архитектуру x86 с целью повышения скорости обработки потоковых данных. Основная идея заключается в одновременной обработке нескольких элементов данных за одну инструкцию.
1.1. Расширение
MMX
Первой SIMD-расширение в свой x86-процессор ввела фирма Intel – это расширение MMX. Оно стало использоваться в процессорах Pentium MMX (расширение архитектуры Pentium или P5) и Pentium II (расширение архитектуры Pentium Pro или P6). Расширение MMX работает с 64-битными регистрами MM0-MM7, физически расположенными на регистрах сопроцессора, и включает 57 новых инструкций для работы с ними. 64-битные регистры логически могут представляться как одно 64-битное, два 32-битных, четыре 16-битных или восемь 8-битных упакованных целых. Еще одна особенность технологии MMX – это арифметика с насыщением. При этом переполнение не является циклическим, как обычно, а фиксируется минимальное или максимальное значение. Например, для 8-битного беззнакового целого x:
обычная арифметика: x=254; x+=3; // результат x=1
арифметика с насыщением: x=254; x+=3; // результат x=255
1.2. Расширение 3
DNow
!
Технология 3DNow! была введена фирмой AMD в процессорах K6-2. Это была первая технология, выполняющая потоковую обработку вещественных данных. Расширение работает с регистрами 64-битными MMX, которые представляются как два 32-битных вещественных числа с одинарной точностью. Система команд расширена 21 новой инструкцией, среди которых есть команда выборки данных в кэш L1. В процессорах Athlon и Duron набор инструкций 3DNow! был несколько дополнен новыми инструкциями для работы с вещественными числами, а также инструкциями MMX и управления кэшированием.
1.3. Расширение
SSE
С процессором Intel Pentium III впервые появилось расширение SSE (Streaming SIMD Extension). Это расширение работает с независимым блоком из восьми 128-битных регистров XMM0-XMM7. Каждый регистр XMM представляет собой четыре упакованных 32-битных вещественных числа с одинарной точностью. Команды блока XMM позволяют выполнять как векторные (над всеми четырьмя значениями регистра), так и скалярные операции (только над одним самым младшим значением). Кроме инструкций с блоком XMM в расширение SSE входят и дополнительные целочисленные инструкции с регистрами MMX, а также инструкции управления кэшированием.
1.4. Расширение
SSE
2
В процессоре Intel Pentium 4 набор инструкций получил очередное расширение – SSE2. Оно позволяет работать с 128-битными регистрами XMM как с парой упакованных 64-битных вещественных чисел двойной точности, а также с упакованными целыми числами: 16 байт, 8 слов, 4 двойных слова или 2 учетверенных (64-битных) слова. Введены новые инструкции вещественной арифметики двойной точности, инструкции целочисленной арифметики, 128-разрядные для регистров XMM и 64-разрядные для регистров MMX. Ряд старых инструкций MMX распространили и на XMM (в 128-битном варианте). Кроме того, расширена поддержка управления кэшированием и порядком исполнения операций с памятью.
1.5. Расширение
SSE
3
Дальнейшее расширение системы команд – SSE3 – вводится в процессоре Intel Pentium 4 с ядром Prescott. Это набор из 13 новых инструкций, работающих с блоками XMM, FPU, в том числе двух инструкций, повышающих эффективность синхронизации потоков, в частности, при использовании технологии Hyper-Threading.
1.6. Поддержка
SIMD
-расширений архитектурой
x
86-64
Процессоры AMD Athlon64 и AMD Opteron с архитектурой x86-64 поддерживают все выше перечисленные SIMD-расширения, кроме SSE3. Кроме того, число XMM регистров у этих процессоров увеличилось до 16 (XMM0-XMM15). Подробное описание типов и команд SSE приведено в приложении.
2.
Встроенные функции потокового SIMD расширения
Типы данных
Для работы с векторными данными, содержащими несколько упакованных значений, используются следующие типы:
__m64 – 64-бит (регистр MMX)
1 * 64-битное целое
2 * 32-битных целых
4 * 16-битных целых
8 * 8-битных целых.
__m128 – 128-бит (регистр XMM):
4 * 32-битных вещественных (SSE),
2 * 64-битных вещественных (SSE2),
2 * 64-битное целых (SSE2),
4 * 32-битных целых (SSE2),
8 * 16-битных целых (SSE2),
16 * 8-битных целых (SSE2).
Для наибольшей эффективности элементы таких типов данных должны быть выровнены в памяти по соответствующей границе. Например, начало массива элементов типа __m64 выравнивается по 8 байтам, а массив элементов __m128 – по 16 байтам. Статические переменные и массивы компилятор выравнивает автоматически. Динамические данные компилятор обычно выравнивает по только величине 4 байта. Если данные векторных типов оказались невыровненными, то для работы с ними следует применять специальные команды невыровненного чтения и записи (они работают медленнее обычных – выровненных). Для выделения памяти с выравниванием используется функция:
void *_mm_malloc(int size, int align)
size – объем выделяемой памяти в байтах (как в malloc),
align – выравнивание в байтах.
Для освобождения памяти, выделенной таким образом, используется функция:
void _mm_free(void *p);
Например:
float *x; // массив для обработки с помощью инструкций SSE
x=(float)_mm_malloc(N*sizeof(float),16);
// … здесь обработка …
_mm_free(x);
Встроенные функции
SSE
для работы с вещественными числами
Заголовочный файл xmmintrin.h содержит объявления встроенных функций (intrinnsics) SSE.
Арифметические функции
| Функция
|
Инструкция
|
Операция
|
R0
|
R1
|
R2
|
R3
|
| _mm_add_ss
|
ADDSS
|
сложение
|
a0 [op] b0
|
a1
|
a2
|
a3
|
| _mm_add_ps
|
ADDPS
|
сложение
|
a0 [op] b0
|
a1 [op] b1
|
a2 [op] b2
|
a3 [op] b3
|
| _mm_sub_ss
|
SUBSS
|
вычитание
|
a0 [op] b0
|
a1
|
a2
|
a3
|
| _mm_sub_ps
|
SUBPS
|
вычитание
|
a0 [op] b0
|
a1 [op] b1
|
a2 [op] b2
|
a3 [op] b3
|
| _mm_mul_ss
|
MULSS
|
умножение
|
a0 [op] b0
|
a1
|
a2
|
a3
|
| _mm_mul_ps
|
MULPS
|
умножение
|
a0 [op] b0
|
a1 [op] b1
|
a2 [op] b2
|
a3 [op] b3
|
| _mm_div_ss
|
DIVSS
|
деление
|
a0 [op] b0
|
a1
|
a2
|
a3
|
| _mm_div_ps
|
DIVPS
|
деление
|
a0 [op] b0
|
a1 [op] b1
|
a2 [op] b2
|
a3 [op] b3
|
| _mm_sqrt_ss
|
SQRTSS
|
квадратный корень
|
[op] a0
|
a1
|
a2
|
a3
|
| _mm_sqrt_ps
|
SQRTPS
|
квадратный корень
|
[op] a0
|
[op] b1
|
[op] b2
|
[op] b3
|
| _mm_rcp_ss
|
RCPSS
|
обратное значение
|
[op] a0
|
a1
|
a2
|
a3
|
| _mm_rcp_ps
|
RCPPS
|
обратное значение
|
[op] a0
|
[op] b1
|
[op] b2
|
[op] b3
|
| _mm_rsqrt_ss
|
RSQRTSS
|
обратное значение квадратного корня
|
[op] a0
|
a1
|
a2
|
a3
|
| _mm_rsqrt_ps
|
RSQRTPS
|
обратное значение квадратного корня
|
[op] a0
|
[op] b1
|
[op] b2
|
[op] b3
|
| _mm_min_ss
|
MINSS
|
минимум
|
[op](a0,b0)
|
a1
|
a2
|
a3
|
| _mm_min_ps
|
MINPS
|
минимум
|
[op](a0,b0)
|
[op](a1,b1)
|
[op](a2,b2)
|
[op](a3,b3)
|
| _mm_max_ss
|
MAXSS
|
максимум
|
[op](a0,b0)
|
a1
|
a2
|
a3
|
| _mm_max_ps
|
MAXPS
|
максимум
|
[op](a0,b0)
|
[op](a1,b1)
|
[op](a2,b2)
|
[op](a3,b3)
|
Функции сравнения
Каждая встроенная функция сравнения выполняет сравнение операндов a и b. В векторной форме сравниваются четыре вещественных значения параметра a с четырьмя вещественными значениями параметра b, и возвращается 128-битная маска. В скалярной форме сравниваются младшие значения параметров, возвращается 32-битная маска, остальные три старших значения копируются из параметра a. Маска устанавливается в значение 0xffffffff для тех элементов, результат сравнения которых истина, и 0x0, где результат сравнения ложь.
| Имя
|
Сравнение
|
Инструкция
|
| _mm_cmpeq_ss
|
равно
|
CMPEQSS
|
| _mm_cmpeq_ps
|
равно
|
CMPEQPS
|
| _mm_cmplt_ss
|
меньше
|
CMPLTSS
|
| _mm_cmplt_ps
|
меньше
|
CMPLTPS
|
| _mm_cmple_ss
|
меньше или равно
|
CMPLESS
|
| _mm_cmple_ps
|
меньше или равно
|
CMPLEPS
|
| _mm_cmpgt_ss
|
больше
|
CMPLTSS
|
| _mm_cmpgt_ps
|
больше
|
CMPLTPS
|
| _mm_cmpge_ss
|
больше или равно
|
CMPLESS
|
| _mm_cmpge_ps
|
больше или равно
|
CMPLEPS
|
| _mm_cmpneq_ss
|
не равно
|
CMPNEQSS
|
| _mm_cmpneq_ps
|
не равно
|
CMPNEQPS
|
| _mm_cmpnlt_ss
|
не меньше
|
CMPNLTSS
|
| _mm_cmpnlt_ps
|
не меньше
|
CMPNLTPS
|
| _mm_cmpnle_ss
|
не меньше или равно
|
CMPNLESS
|
| _mm_cmpnle_ps
|
не меньше или равно
|
CMPNLEPS
|
| _mm_cmpngt_ss
|
не больше
|
CMPNLTSS
|
| _mm_cmpngt_ps
|
не больше
|
CMPNLTPS
|
| _mm_cmpnge_ss
|
не больше или равно
|
CMPNLESS
|
| _mm_cmpnge_ps
|
не больше или равно
|
CMPNLEPS
|
| _mm_cmpord_ss
|
упорядочены
|
CMPORDSS
|
| _mm_cmpord_ps
|
упорядочены
|
CMPORDPS
|
| _mm_cmpunord_ss
|
неупорядочены
|
CMPUNORDSS
|
| _mm_cmpunord_ps
|
неупорядочены
|
CMPUNORDPS
|
| _mm_comieq_ss
|
равно
|
COMISS
|
| _mm_comilt_ss
|
меньше
|
COMISS
|
| _mm_comile_ss
|
меньше или равно
|
COMISS
|
| _mm_comigt_ss
|
больше
|
COMISS
|
| _mm_comige_ss
|
большеили равно
|
COMISS
|
| _mm_comineq_ss
|
не равно
|
COMISS
|
| _mm_ucomieq_ss
|
равно
|
UCOMISS
|
| _mm_ucomilt_ss
|
меньше
|
UCOMISS
|
| _mm_ucomile_ss
|
меньше или равно
|
UCOMISS
|
| _mm_ucomigt_ss
|
больше
|
UCOMISS
|
| _mm_ucomige_ss
|
больше или равно
|
UCOMISS
|
| _mm_ucomineq_ss
|
не равно
|
UCOMISS
|
Операции преобразования
типов
| Имя функции
|
Операция
|
Инструкция
|
| _mm_cvtss_si32
|
Преобразует младший float в 32-битное целое
|
CVTSS2SI
|
| _mm_cvtps_pi32
|
Преобразует два младших float в два упакованных 32-битных целых
|
CVTPS2PI
|
| _mm_cvttss_si32
|
Преобразует младший float в 32-битное целое, отбрасывая дробную часть
|
CVTTSS2SI
|
| _mm_cvttps_pi32
|
Преобразует два младших float в два упакованных 32-битных целых, отбрасывая дробную часть
|
CVTTPS2PI
|
| _mm_cvtsi32_ss
|
Преобразует 32-битное целое в float
|
CVTSI2SS
|
| _mm_cvtpi32_ps
|
Преобразует два упакованных 32-битных целых в два младших float
|
CVTTPS2PI
|
| _mm_cvtpi16_ps
|
Преобразует четыре упакованных 16-битных целых в упакованные float
|
составная
|
| _mm_cvtpu16_ps
|
Преобразует четыре упакованных беззнаковых 16-битных целых в упакованные float
|
составная
|
| _mm_cvtpi8_ps
|
Преобразует четыре младших упакованных 8-битных целых в четыре упакованных float
|
составная
|
| _mm_cvtpu8_ps
|
Преобразует четыре младших упакованных беззнаковых 8-битных целых в четыре упакованных float
|
составная
|
| _mm_cvtpi32x2_ps
|
Преобразует две пары упакованных 32-битных целых в четыре упакованных float
|
составная
|
| _mm_cvtps_pi16
|
Преобразует четыре упакованных float в четыре 16-битных целых
|
составная
|
| _mm_cvtps_pi8
|
Преобразует четыре упакованных float в четыре младших 8-битных целых
|
составная
|
Другие функции
| Имя функции
|
Операция
|
Инструкция
|
| _mm_shuffle_ps
|
перестановка упакованных значений
|
SHUFPS
|
| _mm_shuffle_pi16
|
перестановка упакованных значений
|
PSHUFW
|
| _mm_unpackhi_ps
|
выборка старших значений
|
UNPCKHPS
|
| _mm_unpacklo_ps
|
выборка младших значений
|
UNPCKLPS
|
| _mm_loadh_pi
|
загрузка старших значений
|
MOVHPS reg, mem
|
| _mm_storeh_pi
|
сохранение старших значений
|
MOVHPS mem, reg
|
| _mm_movehl_ps
|
копирование старшей половины в младшую
|
MOVHLPS
|
| _mm_movelh_ps
|
копирование младшей половины в старшую
|
MOVLHPS
|
| _mm_loadl_pi
|
загрузка младших значений
|
MOVLPS reg, mem
|
| _mm_storel_pi
|
сохранение младших значений
|
MOVLPS mem, reg
|
| _mm_movemask_ps
|
создание знаковой маски
|
MOVMSKPS
|
| _mm_getcsr
|
сохранить регистр состояния
|
STMXCSR
|
| _mm_setcsr
|
установить регистр состояния
|
LDMXCSR
|
Команды для инициализации и работы с памятью
Инициализация
памяти
| Имя функции
|
Операция
|
Инструкция
|
| _mm_load_ss
|
загрузить младшее значение и очистить остальные три значения
|
MOVSS
|
| _mm_load1_ps
|
загрузить одно значение во все четыре позиции
|
MOVSS + Shuffling
|
| _mm_load_ps
|
Загрузить четыре значения по выровненному адресу
|
MOVAPS
|
| _mm_loadu_ps
|
Загрузить четыре значения по невыровненному адресу
|
MOVUPS
|
| _mm_loadr_ps
|
Загрузить четыре значения в обратном порядке
|
MOVAPS + Shuffling
|
Инициализация значений
| Имя функции
|
Операция
|
Инструкция
|
| _mm_set_ss
|
устанавливает самое младшее значение и обнуляет три остальных
|
составная
|
| _mm_set1_ps
|
устанавливает четыре позиции в одно значение
|
составная
|
| _mm_set_ps
|
устанавливает четыре значения, выровненные по адресу
|
составная
|
| _mm_setr_ps
|
устанавливает четыре значения в обратном порядке
|
составная
|
| _mm_setzero_ps
|
Обнуляет все четыре значения
|
составная
|
Операции записи
| Имя функции
|
Операция
|
Инструкция
|
| _mm_store_ss
|
записать младшее значение
|
MOVSS
|
| _mm_store1_ps
|
записать младшее значение во все четыре позиции
|
MOVSS + Shuffling
|
| _mm_store_ps
|
записать четыре значения по выровненному адресу
|
MOVAPS
|
| _mm_storeu_ps
|
записать четыре значения по невыровненному адресу
|
MOVUPS
|
| _mm_storer_ps
|
записать четыре значения в обратном порядке
|
MOVAPS + Shuffling
|
| _mm_move_ss
|
записать младшее значение и оставить без изменения три остальных значения
|
MOVSS
|
Поддержка кэш-памяти в
SSE
| Имя функции
|
Операция
|
Инструкция
|
| _mm_prefetch
|
Загружает одну кэш-строку по указанному адресу в кэш-память
|
PREFETCH
|
| _mm_stream_pi
|
Записывает данные в память без записи в кэш
|
MOVNTQ
|
| _mm_stream_ps
|
Записывает данные в память без записи в кэш по адресу, выровненному по 16 байт
|
MOVNTPS
|
| _mm_sfence
|
Гарантирует, что все предшествующие записи в память завершатся до следующей записи.
|
SFENCE
|
3. Использование встроенных функций
SSE
в программе на языке Си
// скалярное произведение векторов
#include <stdio.h>
#include <xmmintrin.h>
#define N 10000000
// «обычная» функция
float inner1(float *x,float *y,int n)
{
float s;
int i;
s=0;
for(i=0;i<n;i++)
s+=x[i]*y[i];
return s;
}
// функция с использованием SSE intrinsics
float inner2(float *x,float *y,int n)
{
float sum;
int i;
__m128 *xx,*yy;
__m128 p,s;
xx=(__m128 *)x;
yy=(__m128 *)y;
s=_mm_set_ps1(0);
for (i=0;i<n/4;i++)
{
p=_mm_mul_ps(xx[i], yy[i]); // векторное умножение четырех чисел
s=_mm_add_ps(s,p); // векторное сложение четырех чисел
}
p=_mm_movehl_ps(p,s); // перемещение двух старших значений s в младшие p
s=_mm_add_ps(s,p); // векторное сложение
p=_mm_shuffle_ps(s,s,1);//перемещение второго значения в s в младшую позицию в p
s=_mm_add_ss(s,p); // скалярное сложение
_mm_store_ss(&sum,s); // запись младшего значения в память
return sum;
}
int main()
{
float *x,*y, s;
long t;
int i;
// выделение памяти с выравниванием
x=(float *)_mm_malloc(N*sizeof(float),16);
y=(float *)_mm_malloc(N*sizeof(float),16);
for (i=0;i<N;i++)
{
x[i]=10*i/N;
y[i]=10*(N-i-1)/N;
}
// Using x87
s=inner1(x,y,N);
printf("Result: %f\n",s);
// Using SSE
s=inner2(x,y,N);
printf("Result: %f\n",s);
_mm_free(x);
_mm_free(y);
return 0;
}
Задание.
1. Реализовать процедуру умножения квадратных матриц (размером кратным четырём) без использования специальных расширений и с использованием расширений SSE, сравнить время выполнения этих реализаций (Обязательное задание
– 10 баллов).
2. В соответствии с вариантом задания реализовать матрично-векторную (с одинаковым размером матриц и векторов кратным четырём) процедуру с использованием расширений SSE (Дополнительное задание
– 7 баллов).
3. С использованием инструкции cpuid
определить наличие расширения SSE (Дополнительное задание
– 3 балла).
4. Крайний срок сдачи – 7 мая 2011 года
.
Варианты.
В предложенных вариантах предполагается, что 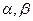 – скаляры, – скаляры, 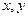 – векторы, – векторы, 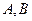 – матрицы: – матрицы:
1. Операция 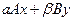 . .
2. Операция 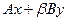 . .
3. Операция 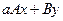 . .
4. Операция 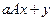 . .
5. Операция 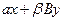 . .
6. Операция 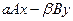 . .
7. Операция 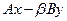 . .
8. Операция 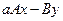 . .
9. Операция 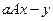 . .
10. Операция  . .
Лабораторная работа № 4
Программирование многоядерных архитектур
Цель работы.
Использование интерфейса OpenMP для программирования простых многопоточных приложений.
Методические указания.
1. Интерфейс
OpenMP
OpenMP – интерфейс прикладного программирования (API) для масштабируемых SMP-систем (симметричные мультипроцессорные системы) в модели общей памяти.
Исполняемый процесс в памяти может состоять из множественных нитей, которые имеют общее адресное пространство, но разные потоки команд и раздельные стэки. В простейшем случае, процесс состоит из одной нити, выполняющую функцию main. Нити иногда называют также потоками, легковесными процессами, LWP (light-weight processes). OpenMP основан на существовании множественных потоков в общедоступной памяти [3]. Схема процесса представлена на рисунке.

Рисунок 8.
Все программы OpenMP начинаются как единственный процесс с главным потоком. Главный поток выполняется последовательно, пока не сталкиваются с первой областью параллельной конструкции. Создание нескольких потоков (FORK) и объединение (JOIN) проиллюстрировано на рисунке.

Рисунок 9.
2. Примеры программ с использованием
OpenMP
2.1. Определение и печать номера потока
#include <omp.h>
#include <stdio.h>
void main ()
{
int nthreads, tid;
/* Fork a team of threads giving them their own copies of variables */
#pragma omp parallel private(tid)
{
/* Obtain and print thread id */
tid = omp_get_thread_num();
printf("Hello World from thread = %d\n", tid);
/* Only master thread does this */
if (tid == 0)
{
nthreads = omp_get_num_threads();
printf("Number of threads = %d\n", nthreads);
}
} /* All threads join master thread and terminate */
}
2.2. Распределение работы
#include <stdio.h>
#include <omp.h>
#define CHUNKSIZE 100
#define N 1000
void main ()
{
int i, chunk;
float a[N], b[N], c[N];
/* Some initializations */
for (i=0; i < N; i++)
a[i] = b[i] = i * 1.0;
chunk = CHUNKSIZE;
#pragma omp parallel shared(a,b,c,chunk) private(i)
{
#pragma omp for schedule(dynamic,chunk) nowait
for (i=0; i < N; i++)
c[i] = a[i] + b[i];
} /* end of parallel section */
}
2.3.
Использование
секций
#include <stdio.h>
#include <omp.h>
#define N 1000
void main ()
{
int i;
float a[N], b[N], c[N], d[N];
/* Some initializations */
for (i=0; i < N; i++)
{
a[i] = i * 1.5;
b[i] = i + 22.35;
}
#pragma omp parallel shared(a,b,c,d) private(i)
{
#pragma omp sections nowait
{
#pragma omp section
for (i=0; i < N; i++)
c[i] = a[i] + b[i];
#pragma omp section
for (i=0; i < N; i++)
d[i] = a[i] * b[i];
} /* end of sections */
} /* end of parallel section */
}
2.4. Параллельная реализация одиночных циклов
#include <stdio.h>
#include <omp.h>
#define N 1000
#define CHUNKSIZE 100
void main ()
{
int i, chunk;
float a[N], b[N], c[N];
/* Some initializations */
for (i=0; i < N; i++)
a[i] = b[i] = i * 1.0;
chunk = CHUNKSIZE;
#pragma omp parallel for shared(a,b,c,chunk) private(i) schedule(static,chunk)
for (i=0; i < n; i++)
c[i] = a[i] + b[i];
}
2.5. Критические секции
#include <omp.h>
void main()
{
int x;
x = 0;
#pragma omp parallel shared(x)
{
#pragma omp critical
x = x + 1;
} /* end of parallel section */
}
2.6.
Редуцируемые
операции
#include <omp.h>
#include <stdio.h>
void main ()
{
int i, n, chunk;
float a[100], b[100], result;
/* Some initializations */
n = 100;
chunk = 10;
result = 0.0;
for (i=0; i < n; i++)
{
a[i] = i * 1.0;
b[i] = i * 2.0;
}
#pragma omp parallel for default(shared) private(i) schedule(static,chunk) \ reduction(+:result)
for (i=0; i < n; i++)
result = result + (a[i] * b[i]);
printf("Final result= %f\n",result);
}
Задание.
1. В соответствии с вариантом задания реализовать алгоритм с использованием интерфейса OpenMP (Дополнительное задание:
варианты 1,2 и 3 – 20 баллов, вариант 4 – 30 баллов).
2. Защита лабораторной работы (Дополнительное задание
– 10 баллов).
3. Крайний срок сдачи – 20 мая 2011 года
.
4. Крайний срок защиты – 25 мая 2011 года
.
Варианты.
1. Скалярное произведение двух векторов.
2. Умножение матрицы на вектор.
3. Умножение матрицы на матрицу.
4. Решение системы линейных алгебраических уравнений методом Гаусса.
Литература
1. Спецификация инструкции cpuid для процессоров Intel http://www.intel.com/Assets/PDF/appnote/241618.pdf
2. Спецификация инструкции cpuid для процессоров AMD http://support.amd.com/us/Embedded_TechDocs/25481.pdf
3. Корнеев В.Д. Параллельное программирование кластеров // Новосибирск. НГТУ. 2008. – 312 с.
|