| Федеральное агентство по образованию
Ухтинский государственный технический университет
ВЫЧИСЛЕНИЕ КООРДИНАТ ТОЧЕК В ТЕОДОЛИТНОМ ХОДЕ
Методические указания к выполнению расчетно-графической работы по дисциплине “Инженерная геодезия”
Ухта 2008
УДК 528.425 (075.8)
Ф 34
Федотов, Н.С. Вычисление координат точек в теодолитном ходе [Текст]: метод. указания / Н.С. Федотов, В.Ю. Дудников, С.Б. Дудникова.– Ухта: УГТУ, 2008.- 14 с., ил.
Методические указания предназначены для студентов специальностей: 130501
Проектирование и эксплуатация магистральных трубопроводов, 250401
Лесоинженерное дело. В методических указаниях рассмотрены вопросы решения обратной геодезической задачи и вычисления координат точек в теодолитном ходе с помощью калькулятора. Содержание методических указаний соответствует рабочей учебной программе.
Методические указания рассмотрены и одобрены на заседании кафедры ТМЛиПГ 27.05.2008 г., протокол №8
Рецензент: О.Н. Бурмистрова, д.т.н., зав. кафедрой ТМЛиПГ Ухтинского государственного технического университета
План 2008 г., позиция 237
Подписано в печать_16.06.2008
_ Компьютерный набор.
Объем 14 с. Тираж 100 экз. Заказ № 220.
© Ухтинский государственный технический университет, 2008
169300, г. Ухта, ул. Первомайская, 13.
Отдел оперативной типографии УГТУ.
169300, г. Ухта, ул. Октябрьская, 13.
1.
Цель и задачи расчетно-графической работы.
Настоящее методическое указание имеет своей целью оказать помощь студентам в обработке результатов полевых измерений и получить координаты точек разомкнутого теодолитного хода.
Геодезические работы, как правило, имеют два этапа: полевые работы (измерения на местности) и камеральные работы (обработка результатов полевых измерений) и составление плана участка местности.
2.
Краткие сведения о разомкнутом теодолитном ходе.
Полевые работы при тахеометрической съемке заключаются в создании на подлежащем к съемке участке ломанной или замкнутой линии, представляющую ту или иную фигуру, ее называют теодолитным ходом (рис. 1). Точки перегибов линии, закрепляемых на местности деревянными кольями или другими знаками, называют вершинами, а прямые, соединяющие вершины – сторонами теодолитного хода.
 Углы при вершинах теодолитного хода измеряют с точностью 30″ теодолитом, а длины сторон – мерными приборами с относительной погрешностью чаще всего с относительной погрешностью 1:2000 (рис. 2). Горизонтальные проложения сторон определяют с учетом угла наклона местности, который также измеряется теодолитом. Опираясь на полученный теодолитный ход, который является плановым обоснованием тахеометрической съемки, производится съемка характерных точек контуров местности (ситуации) с зарисовкой на схематических чертежах, называемых абрисами. Углы при вершинах теодолитного хода измеряют с точностью 30″ теодолитом, а длины сторон – мерными приборами с относительной погрешностью чаще всего с относительной погрешностью 1:2000 (рис. 2). Горизонтальные проложения сторон определяют с учетом угла наклона местности, который также измеряется теодолитом. Опираясь на полученный теодолитный ход, который является плановым обоснованием тахеометрической съемки, производится съемка характерных точек контуров местности (ситуации) с зарисовкой на схематических чертежах, называемых абрисами.
Рис.1.

Рис. 2.
Зная координаты Х,У пунктов государственной геодезической сети (пункты триангуляции - Δ и полигонометрии - □ ) на которые опирается теодолитный ход, решая обратную геодезическую задачу вычисляют α – начальный и конечный дирекционный угол хода.
3.
Исходные данные и материалы, выдаваемые студентам.
3.1. Вариант с исходными данными и результатами полевых измерений
приведен в табл. 1.
Таблица 1
| №
точек
хода
|
Измеренные углы β
(градусы и минуты)
|
Измеренные длины линий d
,
(м)
|
Координаты
|
| Х, (м)
|
У, (м)
|
| п.т. Заимка
|
8292.43
|
2922.15
|
| п.т. Лесной
|
1300
42.2/
|
4922.46
|
5383.77
|
| 348.52
|
| т.1
|
2750
20.8/
|
| 277.15
|
| т.2
|
1270
15.9/
|
| 374.92
|
| т.3
|
2390
51.5/
|
| 381.44
(ν=20
43/
)
|
| т.4
|
1490
57.5/
|
| 293.22
|
| п.п. 43
|
2640
01.9/
|
3696.40
|
5892.75
|
| п.п. 44
|
3523.42
|
5388.85
|
3.2. Бланк “Ведомость вычисления координат” (прил. 1) в который переписываются данные из табл.1.
4.
Решение обратных геодезических задач.
Обратная геодезическая задача – определение длины d
и дирекционного угла a направления отрезка прямой линии по данным координатам его начальной и конечной точек.
Дирекционные углы сторон опорных пунктов п.т. Заимка- п.т. Лесной и п.п. 43 – п.п. 44 определяются решением обратных задач по формулам:
 ; ; 
и далее  . .
Решение обратных задач выполняется с помощью калькулятора, в последовательном порядке, приведенном в табл. 2.
Таблица 2
| №
действий
|
Обозначения
|
Действия
|
1. п.т. Заимка
2. п.т. Лесной
|
1. п.п. 43
2. п.п. 44
|
| 1
|
У2
|
Из задания
|
5383.77
|
5388.85
|
| 2
|
У1
|
Из задания
|
2922.15
|
5892.75
|
| 3
|
∆У
|
У2
- У1
|
2461.62
|
-503.90
|
| 10
|
Sinα
|
С помощью калькулятора
|
0,589854
|
-0,945821
|
| 11
|
d1
|

|
4173,30
|
532,76
|
| 4
|
X2
|
Из задания
|
4922.46
|
3523.42
|
| 5
|
X1
|
Из задания
|
8292.43
|
3696.40
|
| 6
|
∆X
|
X2
- X1
|
-3369.97
|
-172.98
|
| 12
|
Cosα
|
С помощью калькулятора
|
-0,807510
|
-0,324688
|
| 13
|
d2
|

|
4173,29
|
532,76
|
| 7
|
tgr
|

|
0.73046
|
2.91305
|
| 8
|
r
|
С помощью калькулятора
|
36,14656
36 08,8
|
71,05356
71 03,2
|
| 9
|
α
|
По формулам перехода
|
143 51,2
|
251 03,1
|
| 14
|
∆ d
|

|
0,01
|
0.00
|
| 15
|
dсред.
|

|
4173,30
|
532,76
|
Примечание: по знакам приращений координат определяется четверть в которой расположено определяемое направление и, используя формулы перехода (рис. 3.) вычисляют дирекционные углы.
Формулы перехода

Рис. 3.
Вычислительная обработка “Ведомости вычисления координат”.
5.1
Подготовительный этап.
На лицевой стороне бланка “Ведомости вычисления координат” рисуется схема теодолитного хода (рис.2). На схеме показываются измеренные углы β (левые по ходу), начальный и конечный дирекционные углы αнач.
, αкон.
, длины линий d
,
координаты начальной и конечной течек хода Хнач.
, Унач.
, Хкон.
, Укон.
В “Ведомость вычисления координат” из табл. 1 переписываются следующие исходные данные:
5.1.1. Измеренные углы β (колонка 2),
5.1.2. Начальный и конечный дирекционные углы αнач.
, αкон.
(из решения обратных геодезических задач αнач.
– задача п.т. Лесной и п.т. Заимка, αкон.
– задача п.п. 43 и п.п. 44) (колонка 5),
5.1.3. Длины линий (горизонтальные проложения) d
(колонка 6).
Внимание:
длина линии 3-4 (
d
=381.44 м.) имеет угол наклона к горизонту
ν=20
43/
, следовательно вычисляется горизонтальное проложение по формуле
d
=
d
•
Cos
ν = 381.44 •
Cos
20
43/
= 381.01 м.
5.1.4. Координаты начальной и конечной точек хода Хнач.
, Унач.
, Хкон.
, Укон.
(колонки 11,12).
5.2. Вычислительный этап.
Решением прямой геодезической задачи является уравнивание измеренных на местности углов и вычисленных приращений.
Общий алгоритм уравнивания заключается в сравнении суммы измеренных величин с ее теоретическим значением. Разница этих величин называется фактической невязкой, она не должна превышать определенного значения, называемого допустимой (теоретической) невязкой. Значения допустимых невязок определяются по формулам, вытекающим из теории погрешностей, иными словами, они задаются нормативными документами.
Если фактическая невязка не превышает допустимую, ее распределяют на измеренные величины, а если превышает, то результаты полевых измерений бракуются и возвращаются для повторных измерений.
Рассмотрим, например алгоритма уравнивания углов β и приращений координат Dx, Dy.
5.2.1.
Вычисляется сумма измеренных углов ∑ βизм
. В примере (прил. 2) ∑ βизм.
=11870
9.8/
. При суммировании необходимо помнить, что в одном градусе 60/
.
+
1300
42.2/
2750
20.8/
+
1270
15.9/
+
2390
51.5/
+
1490
57.5/
2640
01.9/
---------------------------
11840
189.8/
(189.8/
= 30
09.8 /
) = 11870
09.8/
5.2.2.
Вычисление теоретической суммы углов ∑ βтеор по формуле:
∑ βтеор.
= αкон.
+ 1800
•
n - αнач.
, где n – количество точек хода.
В нашем примере: ∑ βтеор.
= 2510
03.1/
+ 1800
•
6 – 1430
51.2/
= 11870
11.9/
5.2.3.
Вычисление фактической угловой невязки fβ
по формуле:
 = ∑ βизм.
- ∑ βтеор. = ∑ βизм.
- ∑ βтеор.
В нашем примере:  = 11870
09.8/
- 11870
11.9/
= - 2.1/ = 11870
09.8/
- 11870
11.9/
= - 2.1/
Фактическая угловая невязка может быть и с плюсом и с минусом.
5.2.4.
Вычисление допустимой угловой невязки fдоп.
по формуле:
 = 01/
• = 01/
•
 , где n - количество точек хода. , где n - количество точек хода.
 В нашем примере: В нашем примере:  = 01/
• = 01/
•
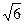 = 2.4/
. = 2.4/
.
Фактическая невязка по абсолютной величине (модулю) не должна превышать допустимую / / ≤ / ≤  . В противном случае необходимо проверить вычисления. Значения ∑ βизм.
, ∑ βтеор.
, . В противном случае необходимо проверить вычисления. Значения ∑ βизм.
, ∑ βтеор.
,  , ,  .
записываются в ведомость вычисления координат (см. прил. 2). .
записываются в ведомость вычисления координат (см. прил. 2).
5.2.5.
Вычисление поправок в измеренные углы по формулам:
Если  £ £ , т.е. невязка допустима, то вычисляют поправки dβ
в измеренные углы путем деления невязки на число углов с округлением поправок до 0,1¢. Поправки имеют знак, противоположный знаку невязки, между собой могут различаться на 0,1/
, их записывают в графу поправки. , т.е. невязка допустима, то вычисляют поправки dβ
в измеренные углы путем деления невязки на число углов с округлением поправок до 0,1¢. Поправки имеют знак, противоположный знаку невязки, между собой могут различаться на 0,1/
, их записывают в графу поправки.
dβ
= 
Контролируют правильность вычисления поправок. Их сумма должна точно равняться невязке с противоположным знаком, т.е.
 В нашем примере: В нашем примере:  = -02.1/
, n=6. = -02.1/
, n=6.
5.2.6.
Вычисление исправленных углов по формуле:
 . .
В нашем примере: 1300
42.2/
+ 0.3/
= 1300
42.5/
2750
20.8/
+ 0.4/
= 2750
21.2/
и т.д.
Контролируют правильность вычисления исправленных углов: сумма исправленных углов должна равняться теоретической сумме углов
∑ βиспр. =
∑ βтеор
5.2.7.
Вычисление дирекционных углов по формулам:
an
+1
= an
+ bиспр.
 180°, 180°,
т.е. дирекционный угол линии последующей равен дирекционному углу линии предыдущей плюс левый угол заключенный между этими сторонами плюс или минус 180°.
При вычислении, если an
+ bиспр.
< 180° , то необходимо прибавить 180, если an
+ bиспр
>180 получилось больше 1800
, то необходимо отнять 1800
.
Контролем вычислений является получение дирекционного угла конечной стороны. Дирекционные углы записываются в графу “Дирекционные углы” (прил. 2)
В нашем примере: a2
= +
1430
51.2/
1300
42.5/
-
2740
33.7/
1800
00.0/
940
33.7/
……………..
a7
= +
1670
00.8/
2640
02.3/
-
3310
03.1/
1800
00.0/
2510
03.1/
= αкон.
5.2.8.
Вычисление приращений координат Dx, Dy по формулам:
∆x =
d
× cos α
∆y =
d × sin α,
где d – длина линии, α – соответствующий дирекционный угол.
Вычисления выполняются с помощью калькулятора. Значения Dx, Dy записываются в графу “Приращения вычисленные” с округлением до сотых (прил. 2). Пример вычисления приращений координат приведён в табл. 3.
Таблица 3
| Задача
|
Последовательность нажатия клавиш
|
Показания индикатора
|
Примечание
|
| Установить режим работы калькулятора
DEG
|
| Значения минут переводятся в градусы
|
33.7/
: 60/
=
|
0.56167
|
| К полученному числу прибавляется значения градусов
|
+ 940
=
|
94.561670
|
Угол α,
выраженный
в градусах
|
| Полученные градусы запоминаются
|
F ЗАП
или
Х →М
|
94.561670
|
Число в регистре
памяти
|
| Вычисляется
Dx
|
F Cos
Х 348.52
|
-0.07953
-27.71852
|
cos α
Dx
|
| |
F ИП
или
МR
|
94.561670
|
Значение α,
вызывается
из памяти
|
| Вычисляется
Dy
|
F Sin или
Sin
Х 348.52
|
0.99683
+ 347.41599
|
sin
α
Dy
|
Значения Dx, Dy записываются в соответствующую графу.
Dx = - 27.72, Dy= + 347.42
5.2.9.
Вычисление невязок приращений координат f
Δ
х
, f
Δy
по формулам:
f
Δ
х
= ΣΔXвыч
.
− ΣΔXтеор
.
,
f
Δy
= ΣΔYвыч
.
− ΣΔYтеор
.
где - ΣΔXвыч
.
, ΣΔYвыч
.
сумма вычисленных приращений координат Dx, Dy.
Теоретическая сумма приращений координат вычисляется по формулам:
ΣΔXтеор.
= Хкон
.
– Xнач
.
ΣΔYтеор
= Yкон
.
– Yнач.
где - Хкон.
, Xнач.
Yкон.
, Yнач.
координаты начальной и конечной точек хода -
Xнач.
= XП.Т.Л.
, Хкон.
= XП.П.43.
, Yнач.
= YП.Т.Л.
, Yкон.
= YП.П.43.
Значения сумм и невязок записывают в ведомость вычисления координат (прил. 2). В нашем примере:
ΣΔXвыч.
= -1225.74, ΣΔYвыч.
= +508.70.
ΣΔXтеор.
=3696.40 – 4922.46 = -1226.06
ΣΔYтеор
= 5892.75 – 5383.77 = 508.98
f
Δ
х
= - 1225.74 – (-1226.06) = +0.32
f
Δy
= 508.70 – 508.98 = - 0.28
5.2.10.
Вычисление абсолютной и относительной невязок хода.
f
абс.
=

f
абс.
f
отн
=-------
Σ
d
где - Σd сумма длин линий хода.
f
отн
вычисляется в виде простой дроби, в числителе которой стоит единица. Если f
отн
>
1/2000, то необходимо проверить вычисления Dx и Dy. Значения f
абс.
и f
отн
записываются в ведомость вычисления координат.
В нашем примере: f
абс
=
 = 0.43 м. = 0.43 м.
f
отн
= 0.43/1674.22 = 1/3894 =1/3900
Чтобы получить f
отн
в виде простой дроби в числителе которой стоит единица, для этого f
абс
/
f
абс
=0.43/0.43 =1,
а в знаменателе Σ
d
/ f
абс
=1674.22/0.43 =3894
и полученное число округляется до сотен метров.
В результате получим f
отн
= 1/3900.
5.2.11.
Вычисление поправок в приращения координат по формулам:
(
δ
x)i
= -
f
Δ
х
/
Σd × di
(
δ
y)i
= -
f
Δy
/
Σd × di
Поправки вводятся пропорционально длинам линий хода с обратным знаком невязок, вычисляются с точностью сотых и записываются в графу “поправки (δ
x
)
I
и (δ
y
)
i
” или над каждым вычисленным приращением Dx, Dy (прил. 2).
Контролем вычисления поправок является равенство:
Σ (
δ
x)i
= -
f
Δ
х
,
Σ (
δ
y)i
= -
f
Δy
Внимание: если равенство не соблюдается, то проверьте правильность округления поправок до сотых или измените их на 0.01.
В нашем примере:
(δ
x
)1
=
- 0.32 /1674.82 x 348.52 = - 0.07 м,
(δ
x
)2
=
- 0.32 /1674.82 x 277.15 = - 0.05 м и т.д.
(δ
y
)1
= - (-0.28) / 1674.82 x 348.52 = + 0.06 м,
(δ
y
)2
= - (-0.28) / 1674.82 x 277.15 = + 0.05 м и т.д.
5.2.12.
Вычисление исправленных значений Dx, Dy по формулам
Dxисп.
i
= Dxвыч.
i
+ δ
xi
Dyисп.
i
= Dyвыч.
i
+ δ
yi
Каждому значению Dxвыч
и Dyвыч
соответствует своя поправка. Контролем служит равенство:
ΣDxисп.
i
= ΣΔXтеор
ΣDyисп.
= ΣΔYтеор
В нашем примере:
Dxисп.1
= -27.72 + (-0.07) = -27.79
Dxисп.2
= -273.01 + (-0.05) = -273.06 и т.д.
Dyисп.1
= 397.42 + (0.06) = 347.48
Dyисп.2
= -47.72 + (0.05) = 47.67 и т.д.
5.2.13.
Вычисление координат Х и Y точек теодолитного хода по формулам:
Хn
+1
= Xn
+ Dxисп.
i
n = 1,2,3,4,5,6
Yn+1
= Yn
+ Dyисп
.i
i= 1,2,3,4,5
Координаты следующей точки равны координатам предыдущей точки плюс соответствующие приращения:
Х2
= X1
+ Dxисп.1
Х3
= X2
+ Dxисп.2
Х4
= X3
+ Dxисп.3
и т.д.
Y2
= Y1
+ Dyисп.1
Y3
= Y2
+ Dyисп.2
и т.д.
Контролем вычисления координат являются равенства:
X6
= Xкон.
; Y6
= Yкон.
В нашем примере: X2
= 4922.46 + (-27.79) = 4894.67
X3
= 4894.67 + (-273.06) = 4621.61
…………………………………..
X6
= 3982.18 + (-285.78)= 3696.40 = Xкон.
Y2
= 5383.77 + 347.48 = 5731.25
Y3
= 5731.25 + (-47.67) = 5683.58
Y6
=5826.81 + 65.94 = 5892.75 = Yкон.
На этом обработка ведомости вычисления координат закончена.
6. Контрольные вопросы
1. Что такое теодолитный ход?
2. Как вычислить угловую невязку fβ
в теодолитном ходе?
3. Как вычислить допустимую угловую невязку fβ
доп
в теодолитном ходе?
4. Как распределить поправки в углы теодолитного хода?
5. Порядок вычисления дирекционных углов.
6. Формулы вычисления приращений координат.
7. Вычисление невязок f
Δ
х
и f
Δy
приращений координат.
8. Что такое абсолютная f
абс
и относительная f
отн
невязки в теодолитном ходе?
9. Как распределяются поправки в приращения координат?
10. Вычисление координат точек теодолитного хода и их контроль.
ЛИТЕРАТУРА
1. Закатов, П.С. Инженерная геодезия [Текст] / П.С. Закатов.- М: Недра, 1976.- 582 с.
2. Федоров, В.И. Инженерная геодезия [Текст] / В.И. Федоров, П.И. Шилов.- М: Недра, 1982.- 357 с.
3. Хейфец, Б.С. Практикум по инженерной геодезии [Текст] / Б.С. Хейфец, Б.Б. Данилевич.- М: Недра, 1979.- 332 с.
Приложение 1
Ведомость вычисления координат вершин теодолитного хода
| № вершин хода
|
Измерен-ные углы
β
|
Поп-равки
υ
|
Исправлен-
ные углы
βиспр.
|
Дирекцион-ные углы
α
|
Длины линий (гориз. пролож.)
|
Приращения координат, м
|
Координаты
|
№ вершин хода
|
| вычисленные
|
исправленные
|
| °
|
¢
|
‘
|
°
|
¢
|
°
|
¢
|
+
-
|
Dх
|
+
-
|
Dу
|
+
-
|
Dх
|
+
-
|
Dу
|
х
|
у
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
| П.т. Заимка
|
-
|
-
|
-
|
-
|
8292.43
|
2922.15
|
П.т. Заимка
|
| 143
|
51,2
|
| П.т. Лесной
|
130
|
42,2
|
4922.46
|
5383.77
|
П.т. Лесной
|
| 348,52
|
|
|
|
|
|
|
|
|
| 1
|
275
|
20,8
|
|
|
|
|
|
|
1
|
| 277,15
|
|
|
|
|
|
|
|
|
| 2
|
127
|
15,9
|
|
|
|
|
|
|
2
|
| 374,92
|
|
|
|
|
|
|
|
|
| 3
|
239
|
51,5
|
|
|
|
|
|
|
3
|
| 381,01
|
|
|
|
|
|
|
|
|
| 4
|
149
|
57,5
|
|
|
|
|
|
|
4
|
| 293,22
|
|
|
|
|
|
|
|
|
| П.П.43
|
264
|
01,9
|
3696.40
|
5892.75
|
П.П.43
|
| 251
|
03,1
|
| П.П.44
|
3523.42
|
5388.85
|
П.П.44
|
Приложение 2
Ведомость вычисления координат вершин теодолитного хода
| № вершин хода
|
Измерен-ные углы
β
|
Поп-равки
υ
|
Исправлен-
ные углы
βиспр.
|
Дирекцион-ные углы
α
|
Длины линий
S, (м)
|
Приращения координат, (м)
|
Координаты, (м)
|
№ вершин хода
|
| вычисленные
|
исправленные
|
| °
|
¢
|
‘
|
°
|
¢
|
°
|
¢
|
+
-
|
Dх
|
+
-
|
Dу
|
+
-
|
Dх
|
+
-
|
Dу
|
х
|
у
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
| П.т. Заимка
|
-
|
-
|
-
|
-
|
8292.43
|
2922.15
|
П.т. Заимка
|
| 143
|
51,2
|
| П.т. Лесной
|
130
|
42,2
|
+0,3
|
130
|
42,5
|
-0,07
|
+0,06
|
4922.46
|
5383.77
|
П.т. Лесной
|
| 94
|
33,7
|
348,52
|
-
|
27,72
|
+
|
347,42
|
-
|
27,79
|
+
|
347,48
|
| 1
|
275
|
20,8
|
+0,4
|
275
|
21,2
|
|
-0,05
|
|
+0,05
|
|
|
|
|
4894,67
|
5731,25
|
1
|
| 189
|
54,9
|
277,15
|
-
|
273,01
|
-
|
47,72
|
-
|
273,06
|
-
|
47,67
|
| 2
|
127
|
15,9
|
+0,3
|
127
|
16,2
|
|
-0.07
|
|
+0,06
|
|
|
|
|
4621,61
|
5683,58
|
2
|
| 137
|
11,1
|
374,92
|
-
|
275,02
|
+
|
254,81
|
-
|
275,09
|
+
|
254,87
|
| 3
|
239
|
51,5
|
+0,3
|
239
|
51,8
|
|
-0,07
|
|
+0,06
|
|
|
|
|
4346,52
|
5938,45
|
3
|
| 197
|
02,9
|
381,01
|
-
|
364,27
|
-
|
111,70
|
-
|
364,34
|
-
|
111,64
|
| 4
|
149
|
57,5
|
+0,4
|
149
|
57,9
|
|
-0,06
|
|
+0,05
|
|
|
|
|
3982,18
|
5826,81
|
4
|
| 167
|
00,8
|
293,22
|
-
|
285,72
|
+
|
65,89
|
-
|
285,78
|
+
|
65,94
|
| П.П.43
|
264
|
01,9
|
+0,4
|
264
|
02,3
|
3696.40
|
5892.75
|
П.П.43
|
| 251
|
03,1
|
| П.П.44
|
3523.42
|
5388.85
|
П.П.44
|
| ∑S=
|
1674,82
|
| ∑∆ хвыч
=
|
-1225,74
|
∑Dувыч.
= +508,70
|
| ∑ βизм.
=
|
1187
|
9,8
|
+2,1
|
1187
|
11,9
|
∑∆ хтеор
=
|
-1226,06
|
∑Dутеор
= +508,98
|
| ∑ βтеор.
=
|
1187
|
11,9
|
ƒDх =
|
+0,32
|
ƒDу= -0,28
|
| ƒβ
=
|
-2,1
|
ƒабс.
= √0,322
+0,282
= 0,43
|
| ƒβдоп.
=
|
±2,4
|
ƒотн..
=
|
0,43
|
=
|
1
|
| |
|
|
1674,22
|
3900
|
|