| 
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Томский политехнический университет
| |
²УТВЕРЖДАЮ²
Декан ЭФФ
____________ Евтушенко Г.С.
«_____» ____________ 2010 г.
|
ПРОЕКТИРОВАНИЕ ЦИФРОВОГО ФИЛЬТРА
МЕТОДОМ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
В ПАКЕТЕ ПРОГРАММ MATHCAD
Методические указания
по выполнению лабораторной работы №5
по курсу “Цифровая обработка сигналов”
ТОМСК 2010
Лабораторная работа №5
Проектирование цифрового фильтра
методом билинейного преобразования в пакете программ Mathcad
1. ЦЕЛЬ РАБОТЫ
1.1. изучение метода билинейного преобразования и различных видов аппроксимации фильтров-прототипов;
1.2. синтез передаточной функции цифрового фильтра (ЦФ) по аналоговому прототипу методом билинейного преобразования;
1.3. исследование переходной и амплитудно-частотной (АЧХ) характеристики фильтра.
2. КРАТКИЕ ПОЯСНЕНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
2.1.
Задачи и методы синтеза цифровых фильтров
Синтез ЦФ в общем случае включает синтез передаточной функции
и структуры фильтра по заданной его частотной или импульсной характеристике, а также оценку требуемой разрядности
чисел для коэффициентов фильтра и отсчетов входного, выходного и внутренних сигналов.
Синтез передаточной функции ЦФ
H(z) по заданной частотной характеристике Hd
(j×ω) заключается в ее аппроксимации
и определении коэффициентов передаточной функции
. Методы синтеза разделяются на аналитические, итерационные и численные.
По виду аппроксимируемой частотной характеристики Hd
(j×ω) различают цифровые фильтры со ступенчато-образной амплитудно-частотной характеристикой (АЧХ) – фильтры нижних частот (ФНЧ), верхних частот (ФВЧ), полосно-пропускающие (ППФ), полосно-заграждающие (ПЗФ), многополосные (МПФ) (рис. 1) и ЦФ с произвольной частотной характеристикой. Могут быть синтезированы также ЦФ с частотной характеристикой цифрового дифференциатора и преобразователя Гильберта.
Так как частотные характеристики ЦФ периодичны по частоте с периодом ωд
и их модуль (АЧХ) и аргумент (ФЧХ) обладают свойствами соответственно четной и нечетной симметрии относительно частот ω = 0 или ωд
/2, то их достаточно задать в полосе частот (0– ωд
/2) или полосе (0–π) нормированных частот λ= ω×Tд
(рис. 1).
Исходными данными для синтеза ЦФ по заданной частотной характеристике (рис.1) являются:
· частоты среза, задерживания ωс
, ωз
, определяющие границы и значения полос пропускания, задерживания и переходных полос фильтра;
· допустимая неравномерность АЧХ фильтра в полосе пропускания (или ослабление на границах полосы пропускания в случае монотонных АЧХ) АП
, дБ;
· минимальное затухание АЧХ в полосе задерживания АЗ
, дБ.
Параметрам АП
, АЗ
, определяющим допустимые погрешности аппроксимации заданной идеализированной АЧХ |Hd
(j×ω)|, соответствуют на рис. 1 уровни допустимого отклонения расчетной АЧХ |H(j×ω)| от 1 в полосе пропускания (1–δ1
) и от нуля в полосе задерживания δ2
: АП
=20×lg[1/(1–δ1
)], дБ; АЗ
=20×lg(1/δ2
), дБ.
Выделенные на рис. 1 пунктиром области образуют поле допусков на погрешности аппроксимации, в которые должна уложиться расчетная аппроксимирующая АЧХ |H(j×ω)|, показанная на рис. 1, в.
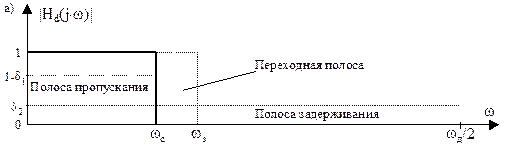
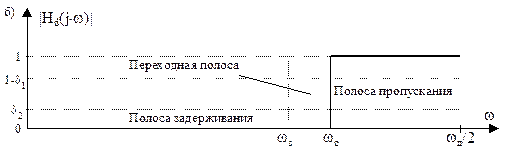

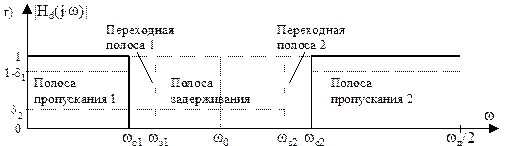
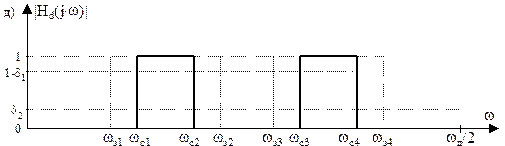
Рис. 1. Примеры задания АЧХ ЦФ
2.2.
Метод билинейного преобразования
Метод билинейного преобразования относится к аналитическим методам
расчета.
По методу билинейного преобразования синтезируемому ЦФ ставится в соответствие некоторый аналоговый фильтр-прототип (АФП ) с передаточной функцией Н(s) и частотной характеристикой H(j×Ω), однозначно связанными с передаточной функцией H(z) и частотной характеристикой H(j×ω) ЦФ:
АФП ЦФ АФП ЦФ
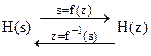 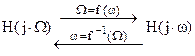
Связь эта определяется прямой s=f(z) и обратной z=f-1
(s) преобразующими функциями и соответствующими им при s=j×Ω и z=ej
×ωTд
преобразованиями частот
Ω=f(ω), ω=f-1
(Ω) аналогового и цифрового фильтров.
С помощью этих преобразований определяются требования к АФП, по которым хорошо разработанными методами синтезируется его передаточная функция H(s), преобразуемая затем в искомую передаточную функцию ЦФ H(z).
Преобразующие функции должны удовлетворять следующим условиям:
· левая S-полуплоскость s=σ+j y, σ<0, в которой размещаются полюсы устойчивого АФП, должна однократно отображаться внутрь круга единичного радиуса |z|<1, в котором на Z-плоскости размещаются полюса устойчивого ЦФ, т.е. устойчивому АФП должен соответствовать устойчивый ЦФ;
· вся мнимая ось частот j×Ω АФП, Ω=(0 ± ∞), должна однократно, т.е. в один обход, отображаться на окружность единичного радиуса Z-плоскости  , ω=(0 ± ωд
/2), обеспечивая близость частотных характеристик обоих фильтров. , ω=(0 ± ωд
/2), обеспечивая близость частотных характеристик обоих фильтров.
Этим условиям отвечает билинейное преобразование, которое определяется следующим образом:
| s=f(z)=(2/T)[(1–z-1
)/(1+z-1
)]
|
(1)
|
Можно также найти обратное соотношение
| z-1
=[(2–s×T)/(2+s×T)]
|
(2)
|
Из свойств процедуры перехода на основе билинейного преобразования следует, что мнимая ось S-плоскости отображается в единичную окружность в Z-плоскости (где |z|=1)

Рис. 2. Свойства процедуры перехода на основе билинейного преобразования
Билинейное преобразование – однозначная функция. Это означает, что каждой точке в Z-плоскости соответствует точно одна точка в s-плоскости и наоборот. Из этого свойства однозначности следует, что отсутствует эффект наложения спектров
при билинейной процедуре отображения.
Методика расчета цифровых фильтров на основе метода билинейного преобразования включает в себя нахождение подходящей передаточной функции Н(s) аналогового фильтра и применение к ней билинейного преобразования для получения передаточной фикции H(z) требуемого цифрового фильтра
| 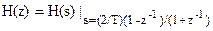
|
(3)
|
При этом преобразовании будут сохраняться и частотные характеристики, и свойства устойчивости аналогового фильтра. Однако это не означает, что частотные характеристики аналогового и цифрового фильтра идентичны, одинакова только их «форма». Например, если амплитудно-частотная характеристика аналогового фильтра монотонно спадает при 0 <W< ¥, то соответствующий цифровой фильтр, полученный с помощью соотношения (3), будет обладать монотонно спадающей АЧХ при 0 <w< ¥,. То есть, если АЧХ аналогового фильтра имеет k подъемов и спадов при 0 <W< ¥, то и амплитудно-частотная характеристика соответствующего цифрового фильтра будет обладать k подъемами и спадами.
В результате перехода к нормированным частотам ЦФ частотные преобразования принимают вид
| 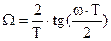
|
(4)
|
Характер деформации частот при билинейном преобразовании показан на рис. 3.
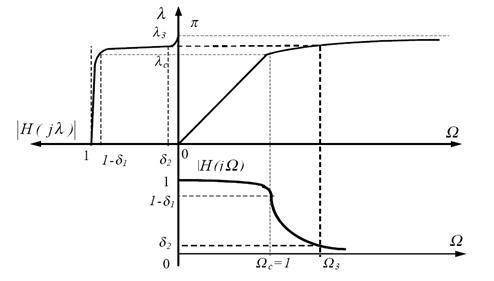
Рис. 3. Преобразование АЧХ аналогового ФНЧ в АЧХ цифрового ФНЧ
Для обеспечения равенства 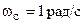 необходимо деформировать частоту аналогового ФНЧ – прототипа: необходимо деформировать частоту аналогового ФНЧ – прототипа: 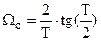 . .
Билинейное преобразование обеспечивает простую процедуру перехода от аналоговых к цифровым фильтрам и сохраняет вид частотных характеристик при преобразовании. Это означает, что широкополосные аналоговые фильтры с крутой переходной областью отображаются в широкополосные цифровые фильтры без эффекта наложения
. В этом заключается основное преимущество этого метода по сравнению с методом инвариантности импульсной характеристики. Недостатком билинейного преобразования является то, что нелинейность соотношения между цифровой частотой w и аналоговой частотой Ω приводит к искажению частотных характеристик
аналоговых фильтров. Кроме того, при этом преобразовании не сохраняется импульсная характеристика
.
2.3.
Порядок синтеза РЦФ по аналоговому прототипу
Возможны два метода проектирования ЦФ по аналоговому прототипу.
В первом методе расчет аналогового фильтра-прототипа (АФП) начинается с нахождения соответствующего аналогового фильтра-прототипа низких частот (АФПНЧ). В дальнейшем используется подходящее аналоговое частотное преобразование
для перевода этого прототипа низких частот в требуемый АФП. Наконец, на основе процедуры отображения
этот аналоговый фильтр преобразуется в желаемый цифровой БИХ-фильтр (фильтр с бесконечной импульсной характеристикой), который удовлетворяет предъявленным требованиям. Полностью эта процедура расчета показана на рис. 3.а.
Процедуры перехода на основе метода инвариантности импульсной характеристики
и метода Эйлера
не обеспечивают хороших методов расчета цифровых фильтров, если полоса аналогового фильтра не ограничена низкими частотами. Метод билинейного преобразования
(из-за нелинейного соотношения между цифровой частотой w и аналоговой частотой W) дает лучшие результаты только для тех частотных характеристик аналогового фильтра, которые представляют собой ступенчато-образную функцию. Это означает, что процедура отображения
(рис. 3.а) не обеспечивает хороших методов расчета фильтров верхних частот, заграждающих и некоторых типов полосовых фильтров.
Для исключения этих недостатков используется другой подход к расчету цифровых БИХ-фильтров. Такой способ изображен на рис. 3.б. В этом случае процедура отображения
всегда имеет дело с нормированным цифровым прототипом низких частот. Следовательно, рассмотренные в предыдущих подразделах три процедуры перехода смогут обеспечить хорошие результаты. В основном этот подход состоит в нахождении подходящего нормированного аналогового фильтра-прототипа низких частот. Аналоговый прототип отображается в цифровой фильтр-прототип низких частот (ЦФПНЧ
). Наконец, используется цифровое частотное преобразование
для перехода от цифрового прототипа низких частот к окончательному варианту, т.е. цифровому фильтру с подходящими характеристиками в полосе пропускания и полосе задерживания и удовлетворяющему предъявленным требованиям.

а) б)
Рис. 3. Процедуры расчета цифровых фильтров
2.4.
Синтез аналогового ФНЧ-прототипа (АФПНЧ)
Синтез АФПНЧ включает выбор аппроксимирующей функции, определение порядка фильтра m, значений нулей s0i
и полюсов spi
и передаточной функции по заданным граничным частотам Ωс
= 1, Ωз
и допускам на погрешности аппроксимации δ1
, δ2
( Aп
, Aз
).
Нули и полюса синтезированного АФПНЧ полностью определяют его передаточную функцию H(s):
| 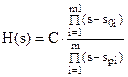
|
(5)
|
где С – нормирующий множитель; m1
– число конечных нулей (m1
< m).
Следует отметить, что полюса АФПНЧ являются вещественными или комплексно-сопряженными числами (со знаком минус перед реальной частью), а конечные нули чисто мнимыми.
Синтез АФПНЧ заключается в аппроксимации его заданной идеализированной ЧХ с помощью соответствующих аппроксимирующих функций.
В качестве аппроксимирующих функций используются полиномы и дроби. К полиномиальным относятся аппроксимации Тейлора (фильтры Баттерворта), Чебышева, к дробным – Кауэра–Золоторева (эллиптические фильтры), Чебышева инверсная.
Передаточные функции фильтров с полиномиальной аппроксимацией не имеют конечных нулей, их частотные характеристики монотонны в полосе задерживания.
У фильтров с дробной аппроксимацией передаточные функции имеют нули на конечных частотах в полосе задерживания, а частотные характеристики – пульсации (в том числе равноволновые) в этой полосе. Фильтры Чебышева и эллиптические имеют равноволновые пульсации и в полосе пропускания.
Типичные графики частотных характеристик нормализованного АФПНЧ с полиномиальной и дробной аппроксимациями приведены на рис. 4.
Для частотных характеристик с равноволновыми пульсациями на графиках указаны соответствующие им частоты нулей и полюсов Ωpi
, Ω0i
ПФ.
Фильтры с дробной аппроксимацией обеспечивают лучшие характеристики затухания при одинаковом порядке фильтра или меньшее значение порядка при заданном затухании частотной характеристики.
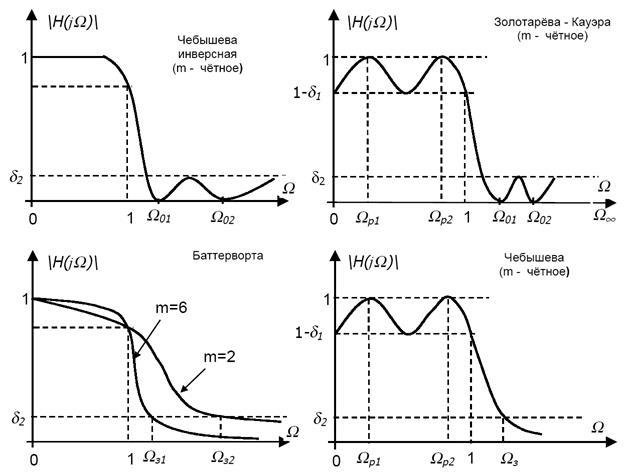 Рис. 4. Графики частотных характеристик нормализованного АФПНЧ, соответствующие различным аппроксимирующим функциям Рис. 4. Графики частотных характеристик нормализованного АФПНЧ, соответствующие различным аппроксимирующим функциям
Фильтр Баттерворта.
Аппроксимация АФПНЧ Баттерворта имеет вид
| 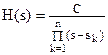
|
(6)
|
где 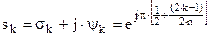 , С – константа нормирования. , С – константа нормирования.
На практике порядок фильтра Баттерворта определяется по заданному ослаблению АЗ
на некоторой частоте WЗ
.
| 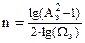
|
(7)
|
Если фильтр имеет четный порядок n, то удобно представлять передаточную функцию фильтра в виде произведения биквадратных звеньев
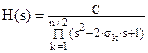 , , 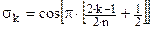 . .
Фильтр Чебышева 1.
Аппроксимация АФПНЧ Чебышева 1 при порядке фильтра n имеет вид
| 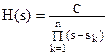
|
(8)
|
где 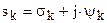 , ,  , , 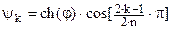 , ,  , , 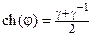 , , 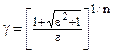 , e – пульсации в полосе пропускания. , e – пульсации в полосе пропускания.
На практике порядок фильтра Чебышева 1 определяется по заданному ослаблению АЗ
на некоторой частоте WЗ
и пульсации в полосе пропускания e.
| 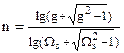 , , 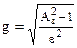 . .
|
(9)
|
Если фильтр имеет четный порядок n, то удобно представлять передаточную функцию фильтра в виде произведения биквадратных звеньев
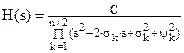 . .
Фильтр Чебышева 2 (инверсный).
Аппроксимация АФПНЧ Чебышева 2 (инверсная) имеет вид
| 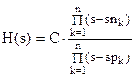
|
(10)
|
где  – полюса, – полюса, 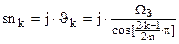 – нули. – нули.
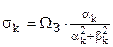 , ,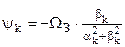 , ,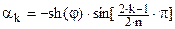 , ,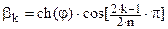 , ,  , , 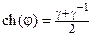 , , 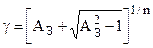 . .
На практике порядок фильтра Чебышева 2 также определяется по заданному ослаблению АЗ
на некоторой частоте WЗ
и пульсации в полосе пропускания (выражение 9).
Если фильтр имеет четный порядок n, то удобно представлять передаточную функцию фильтра в виде произведения биквадратных звеньев
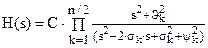 . .
2.5.
Переход от АФПНЧ к ЦФ заданного типа
Аналоговый фильтр-прототип низких частот (АФПНЧ) преобразуется к требуемому аналоговому фильтру-прототипу (АФП) с помощью следующих частотных преобразований:
АФПНЧ-АФНЧ
: 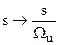 (фильтр низких частот); (фильтр низких частот);
АФПНЧ-АФВЧ
:  (фильтр высоких частот); (фильтр высоких частот);
АФПНЧ-АПФ
: 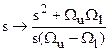 (полосовой фильтр); (полосовой фильтр);
АФПНЧ-АРФ
:  (режекторный фильтр). (режекторный фильтр).
Wu
– верхняя частота среза, Wl
– нижняя частота среза.
Полученный АФП преобразуется в требуемый ЦФ с помощью билинейного преобразования (1, 3).
АФПНЧ может быть преобразован в ЦФПНЧ путем билинейного преобразования (1, 3). Далее выполняются частотные преобразования для получения требуемого ЦФ:
ЦФПНЧ-ЦФНЧ
: 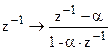 , , 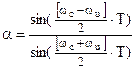 ; ;
ЦФПНЧ-ЦФВЧ
: 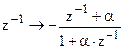 , , 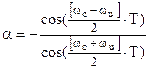 ; ;
ЦФПНЧ-ЦПФ
: 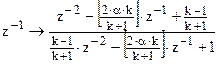 , , 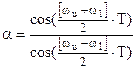 , , 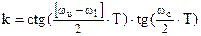 ; ;
ЦФПНЧ-ЦРФ
: 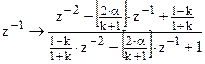 , , 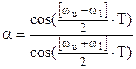 , , 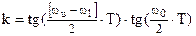 . .
wu
– верхняя частота среза, wl
– нижняя частота среза, w0
– центральная частота ПФ и РФ, wс
– частота среза ЦФПНЧ, T – период дискретизации.
2.6.
Особенности синтеза ЦФ методом билинейного преобразования в
Mathcad
Особенности расчета ЦФ в пакете программ Mathcad нагляднее всего отобразить на конкретном примере.
В качестве примера далее показан расчет цифрового полосового фильтра (ПФ) с аппроксимацией Чебышева 1 рода, порядок АФПНЧ – 2.
2.6.1. Ввод исходных данных

2.6.2. Расчет полюсов нормированного ФНЧ

2.6.3. Расчет АЧХ фильтра-прототипа


Рис. 5. График АЧХ АФП (полосовой фильтр Чебышева 1 рода)
2.6.4. Расчет коэффициентов ЦФ

2.6.5. Расчет АЧХ синтезированного ЦФ
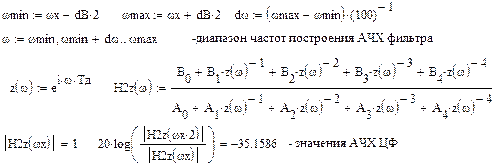

Рис. 6. График АЧХ синтезированного ЦФ (полосовой фильтр Чебышева 1 рода)
2.6.6. Реакция ЦФ на гармонический сигнал


Рис. 7. Реакция ЦФ на гармонический сигнал (fx=100 Гц)
2.6.7. Реакция ЦФ на ступенчатое воздействие
При моделировании переходной характеристики
ЦФ
ступенчатое входное воздействие задается следующим образом
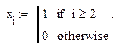

Рис. 8. Переходная характеристика ЦФ
2.6.8. Расчет полюсов ЦФ
Зная коэффициенты знаменателя передаточной функции ЦФ (матрица A), можно определить полюса ЦФ. Для этого необходимо сначала инвертировать порядок следования коэффициентов в матрице (поскольку в знаменателе передаточной функции ЦФ коэффициенты матрицы A соответствуют переменной z-1
).

Если модули полюсов ЦФ меньше 1, то ЦФ устойчивый. В данном случае все полюса лежат внутри окружности единичного радиуса, следовательно, ЦФ устойчивый.
2.7.
Особенности синтеза других типов ЦФ
2.7.1. Полосовой фильтр (ПФ) Баттерворта (АФПНЧ 2 порядка)
Коэффициенты фильтра рассчитываются так же, как показано выше в примере расчета ПФ Чебышева 1 рода (АФПНЧ 2 порядка), п. 2.6
, полюса фильтра-прототипа определяются выражениями

2.7.2. ФНЧ Чебышева 1 рода (АФПНЧ 2 порядка)
Расчет полюсов фильтра аналогичен показанному в примере расчету полосового фильтра Чебышева 1 рода (АФПНЧ 2 порядка), п. 2.6
.
При переходе от нормированного АФПНЧ к АФП используется преобразование
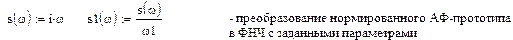
Коэффициенты фильтра рассчитываются следующим образом:
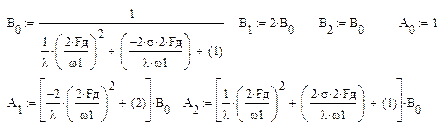
Очевидно, что порядок цифрового фильтра равен при этом 2. Следовательно, уменьшается количество слагаемых числителя и знаменателя передаточной функции ЦФ
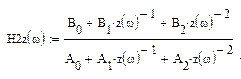 , ,
а также количество обнуляемых выходных отсчетов и порядок алгоритма работы цифрового фильтра.

 . .
3. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
При выполнении лабораторной работы используется пакет программ Mathcad версии 2000 и выше.
4. ПРОГРАММА ЛАБОРАТОРНОЙ РАБОТЫ
4.1. Выполнить синтез АФ-прототипа, в результате которого получить значения его полюсов PP и нулей P0, рассчитать и проанализировать АЧХ АФ-прототипа (АФП).
4.2. Рассчитать коэффициенты передаточной функции ЦФ, а также значения полюсов ЦФ. Проанализировать положение полюсов и нулей на комплексной Z-плоскости.
4.3. Рассчитать и проанализировать АЧХ ЦФ, проверить соответствие АЧХ заданным требованиям.
4.4. Найти отклик фильтра на сигнал в виде ступеньки – переходную характеристику фильтра.
4.5. Найти отклики фильтра на гармонические сигналы в полосе пропускания и полосе задерживания, оценить избирательные свойства фильтра.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
5.1. Что такое импульсная характеристика и передаточная функция ЦФ?
5.2. Как найти передаточную функцию ЦФ по разностному уравнению?
5.3. Как определяется частотная характеристика ЦФ?
5.4. Что такое порядок ЦФ и как сказывается его значение при реализации фильтра?
5.5. Что такое нули и полюса передаточной функции ЦФ?
5.6. Как определить устойчивость ЦФ по значениям его нулей и полюсов?
5.7. Как найти значения нулей и полюсов биквадратного звена по его коэффициентам?
5.8. Что такое билинейная преобразующая функция? Как преобразуются частоты аналогового и цифрового фильтров при билинейном преобразовании?
5.9. Как определяются требования к аналоговому фильтру-прототипу в методе билинейного преобразования?
5.10. Каковы особенности аппроксимирующих функций, используемых при синтезе ЦФ? Как зависит порядок синтезируемого ЦФ от вида аппроксимирующей функции?
5.11. Как преобразуется аналоговый ФНЧ-прототип в цифровой ПФ, ФНЧ, ФВЧ, РФ?
5.12. Какая функция Mathcad позволяет рассчитать полюса ЦФ по его коэффициентам? Как определить устойчивость ЦФ по его полюсам?
5.13. Записать выражение для тестового сигнала при определении переходной характеристики ЦФ.
5.14. Записать алгоритм работы ЦФ 3 порядка в программе Mathcad.
5.15. Как определяется передаточная функция полосового фильтра-прототипа в программе Mathcad?
6. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОГО ЗАДАНИЯ
6.1. Подготовить и ввести в программу исходные данные (п. 2.6.1
) в соответствии с заданным вариантом (по номеру компьютера), необходимые для синтеза цифрового ФНЧ
: аппроксимация – по Чебышеву 1
(п. 2.7.2
); частота среза Fс
; коэффициент усиления K0; порядок фильтра-прототипа N=2, пульсации в полосе пропускания – 1дБ.
| Вариант
|
1
|
2
|
3
|
4
|
5
|
6
|
| Fс
|
100 Гц
|
200 Гц
|
300 Гц
|
400 Гц
|
500 Гц
|
600 Гц
|
| K0
|
10
|
20
|
30
|
40
|
50
|
60
|
При расчете необходимо внести предыскажение частоты среза Fс для компенсации искажения, вносимого билинейным преобразованием. При этом получаем частоту среза фильтра-прототипа F1.
6.2. Выполнить расчет полюсов АФП и анализ их расположения на комплексной плоскости (п. 2.6.2
).
6.3. Выполнить расчет передаточной функции и построить график АЧХ фильтра-прототипа (п. 2.6.3
).
6.4. Выполнить расчет коэффициентов ЦФ (п. 2.6.4
).
6.5. Выполнить расчет полюсов ЦФ и анализ их расположения на комплексной плоскости (п. 2.6.8
).
6.6. Построить АЧХ ЦФ (п. 2.6.5
). По графику АЧХ проверить ее соответствие заданным требованиям. Записать значения АЧХ на частотах среза и задерживания (2×Fc
).
6.7. Построить переходную характеристику цифрового фильтра и определить время установления (п. 2.6.7
).
6.8. Определить отклик ЦФ на входной гармонический сигнал (п. 2.6.6
) с частотой Fx=Fc
и единичной амплитудой. Проверить правильность расчетов по значениям АЧХ.
6.9. Определить отклик ЦФ на входной гармонический сигнал (п. 2.6.6
) с частотой Fx=2×Fc
и единичной амплитудой. Проверить правильность расчетов по значениям АЧХ.
6.10. Выполнить синтез (п.п. 6.1 – 6.9)
цифрового полосового фильтра (ПФ) с аппроксимацией Баттерворта 2 порядка, полоса пропускания DF=0.1×Fc
. Частота среза Fc
остается прежней.
7. СПИСОК ЛИТЕРАТУРЫ
1. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. /Пер. с англ. под ред. Ю.Н. Александрова. – М.: Мир, 1978. – 848 с.
2. Гольденберг Л.М. и др. Цифровая обработка сигналов. – 2-е изд., перераб. и доп. – М.: Радио и связь, 1990. – 256 с.
3. Каганов В.И. Радиотехника+компьютер+Mathcad. – М.: Горячая линия - Телеком, 2001. – 416 с.
4. Глинченко А.С. Цифровая обработка сигналов: учебное пособие. В 2 ч. Ч.1. – Красноярск: Изд-во КГТУ, 2001. – 199 с.
5. Сергиенко А.Б. Цифровая обработка сигналов. – СПб.: Питер, 2003. – 604 с.
ПРОЕКТИРОВАНИЕ ЦИФРОВОГО ФИЛЬТРА
МЕТОДОМ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
В ПАКЕТЕ ПРОГРАММ MATHCAD
Методические указания к лабораторной работе №5
по курсу “Цифровая обработка сигналов”
Составитель Якимов Евгений Валерьевич
|