| ГОСУДАРСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ ПО РЫБОЛОВСТВУ
Астраханский государственный технический университет
Институт информационных технологий и коммуникаций
Кафедра
АСОИУ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению практических работ для студентов специальности
220200 «Автоматизированные системы обработки информации и управления» по дисциплине
«Основы теории автоматического управления»
Астрахань - 2004 г.
Авторы: асс. кафедры АСОИУ Щербатов И.А.
Рецензент: ст.пр. кафедры АСОИУ к.т.н. Антонов О.В.
Методические указания предназначены для студентов специальности 220200 «Автоматизированные системы обработки информации и управления», выполняющих практические работы по дисциплине «Основы теории автоматического управления».
Методические указания содержат задания для выполнения работ по классической теории автоматического управления.
Методическое пособие утверждено на заседании кафедры АСОИУ института ИТиК от _12
_ _ноября
_ 2004 г., протокол №_4
_.
СОДЕРЖАНИЕ
Практическая работа №1. «Анализ технологического процесса как объекта управления»………………………………………....4.
Практическая работа №2. «Переходные процессы в системах автоматического регулирования»……………………………….10
Практическая работа №3. «Построение временных характеристик типовых динамических звеньев»………………30
Практическая работа №4. «Преобразование структурных
схем»………………………………………………………………34
Практическая работа №5. «Устойчивость линейных
систем»……………………………………………………………37
Практическая работа №6. «Построение переходных процессов. Расчет настроек регулятора»……………………………………42
Список рекомендованной литературы……………………….…52
Практическая работа №1. «Анализ технологического процесса как объекта управления».
1. Цель работы:
1.1. Научиться производить анализ технологического процесса как объекта управления.
1.2. Изучить основные принципы регулирования.
2. Общие сведения.
Теория автоматического управления (ТАУ) является теоретической базой разработки большинства автоматических устройств. Предметом изучения ТАУ являются принципы построения, методы анализа и синтеза широко распространенных систем автоматического регулирования и управления.
Основоположником ТАУ, возникшей немногим более века назад, является проф. Петербургского технологического института И.А. Вышнеградский (1831—1895). Основы ТАУ были изложены в его работе "О регуляторах прямого действия" (1876 г.) В этой работе он впервые показал, что процессы в устройстве управления и связанном с ним объектом неразрывно связаны между собой и требуют совместного исследования.
В устройствах управления важное место занимает проблема обеспечения устойчивости движения. Основоположником строгой теории устойчивости является профессор Харьковского университета А.М. Ляпунов (1857-1918).
Дадим несколько базовых определений.
Управление
– осуществление совокупности воздействий на какой-либо процесс, выбранных из множества возможных на основании информации о внутренних и внешних условиях протекания этого процесса и направленных на поддержание условий протекания этого процесса или улучшение его в соответствии с некоторой заданной целью.
Производственный, технологический или технический объект, нуждающийся для определенного взаимодействия с другими объектами или процессами в специально организованном управляющем воздействии, называется объектом управления
(ОУ).
Более частным случаем понятия "управление
" является понятие "регулирование
". Регулирование
- поддержание каких-либо величин, характеризующих процесс, на определенных значениях или изменение их по какому-либо закону.
Регулируемая
(управляемая
) величина – параметр, который является определяющим для нормального протекания управляемого процесса.
Заданное значение
Хз– значение регулируемой
(управляемой
) величины, которое должно обеспечиваться системой автоматического регулирования
.
Регулятор
– техническое устройство, реализующее функцию автоматического регулирования.
Система автоматического регулирования
– совокупность объекта управления и определенным образом присоединенного к нему регулятора, находящихся во взаимодействии.
Регулирующее воздействие
Хр – вырабатываемое регулятором изменение входного параметра объекта, направленное на удовлетворение целей управления.
Управляющее
(задающее
) воздействие – изменение заданного значения Хз
Возмущающее воздействие
Хв – изменение входного параметра объекта, не являющееся следствием работы системы автоматического регулирования.
Рассмотрим основные принципы регулирования используемые в ТАУ.

Рис. 1. Типовая структурная схема системы автоматического регулирования.
a) Регулирование по разомкнутому циклу.
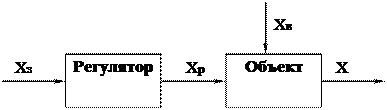
б) Регулирование по возмущению.

в) Регулирование с обратной связью.
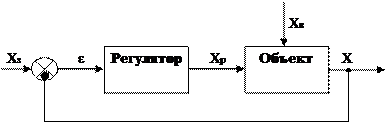
г) Комбинированная система.

3. Задание на практическую работу.
3.1.Произвести анализ процесса как объекта управления (определить границы объекта управления, выделить регулируемые, управляющие и возмущающие величины, дать характеристику объекта по самовыравниванию, оценить динамические характеристики по управлению и возмущению, сформулировать цель управления)
3.2.Выбрать принцип регулирования и обосновать сделанный выбор.
3.3.Предложить техническую реализацию системы автоматического регулирования.
3.4.По структурной схеме САР детализировать звенья и связи.

Рис. 2. Развернутая схема системы автоматического регулирования.
ЗУ – задающее устройство, СУ – сравнивающее устройство, Р – регулятор, У – усилитель, ИМ - исполнительный механизм, РО – регулирующий орган, ОУ – объект управления, ЧЭ – чувствительный элемент, ПДП – преобразователь дистанционной передачи.
3.5.Произвести классификацию САР.
4. Варианты заданий на практическую работу.
1. Поддержание микроклимата в помещении.
2. Холодильная камера.
3. Сливной бачок для унитаза.
4. Дверная система
5. Телообменник.
6. Паровая машина.
7. Духовой шкаф.
8. Печь отпуска металлоизделий.
9. Водонапорная башня.
10. Система вторичного электропитания.
11. Печь-утилизатор.
12. Сушилка для томатной пасты.
5. Контрольные вопросы.
1. Дайте определение понятия управления?
2. Какие принципы регулирования Вам известны?
3. Что называется вектором выходного состояния объекта управления?
4. Что называется возмущающим воздействием?
5. Что называется структурной схемой САР.
6. Укажите на основные принципы классификации систем автоматического управления?
7. Что называется ошибкой управления?
8. Назовите основные причины отклонения вектора выходного состояния от требуемого значения?
9. Нарисуйте структурную схему объекта управления?
10. Для каких целей необходимы управляющие воздействия?
11. Что называется управляющим устройством?
12. Что называется системой автоматического регулирования?
Практическая работа №2. «Переходные процессы в системах автоматического регулирования».
1. Цель работы:
1.1. Изучить виды переходных процессов.
1.2. Изучить количественные показатели качества переходных процессов.
2. Общие сведения.
Устойчивость, то есть способность к затуханию переходных процессов, является необходимым, но далеко не достаточным условием практической пригодности систем. Этот критерий позволяет очень грубо оценить переходные процессы. Рассмотрим, как выглядят переходные характеристики для трех основных режимов с точки зрения устойчивости.

Рис. 1. Виды переходных характеристик.
Использовав, как показано на рис. 1, критерий устойчивости по виду переходной характеристики (переходного процесса), мы можем сказать, что система устойчива, если переходный процесс затухает. Однако система может быть устойчивой, но ее переходные процессы, в зависимости от изменения параметров, будут сильно различаться, как это показано на рис. 2.

Рис. 2. Виды устойчивых переходных характеристик.
Мы видим, что эти процессы существенно отличаются по виду, имеют разные частоту колебаний, время завершения, амплитуду отклонения от заданной величины. В связи с этим возникает необходимость сравнения, оценки устойчивых временных характеристик систем.
Следует отметить, что специалистов интересует не только переходные процессы при изменении управляющих воздействий, но и переходные процессы при изменении возмущающих воздействий.
Таким образом, важным понятие для систем управления является понятие качества переходных процессов, то есть становится важным сам характер протекания процессов, особенно такие факторы, как длительность, колебательность и динамическое отклонение регулируемой переменной от заданной величины.
Для оценки качества переходных процессов требуются характеристики, критерии или показатели качества, которые могут быть выражены численно.
Критерии качества имеют следующие области применения:
1. Сравнительный анализ систем автоматического управления при изменении параметров объекта управления, или при сравнении систем разного вида для одного и того же объекта управления.
2. Синтез, выбор параметров систем автоматического управления, обеспечивающих заданные критерии качества переходных процессов, требованиям технического задания на разработку системы.
Известно, что переходный процесс в системе управления зависит не только от свойств самой системы, но и от характера (вида) входного воздействия. Поэтому поведение системы при оценке качества переходных процессов рассматривают при типовых внешних воздействиях. В качестве таких типовых воздействий чаще всего используют:
· единичную ступенчатую функцию, реже, линейнонарастающий сигнал,
· воздействие гармонической функцией.
Оценки качества делятся на две группы:
1. Прямые показатели качества переходных процессов. Они характеризуют непосредственно сам переходный процесс, реакцию системы на типовое воздействие, чаще всего, на единичную ступенчатую функцию.
2. Косвенные показатели (критерии) качества. Они оценивают качество переходных процессов по другим характеристикам системы, таким как частотные характеристики, характер и расположение корней характеристического уравнения (полюсов передаточной функции), интегралы временной функции переходного процесса.
Оценка качества переходного процесса при воздействии ступенчатой функции.
Прямые оценки качества определяют по графику переходной характеристики системы управления 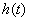 , то есть при воздействии на систему единичной ступенчатой функции – , то есть при воздействии на систему единичной ступенчатой функции –

и при нулевых начальных условиях, или по кривой переходного процесса регулируемой переменной 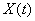 при воздействии на вход ступенчатой функции с амплитудой, соответствующей номинальному или иному определенному значению регулируемой переменной. при воздействии на вход ступенчатой функции с амплитудой, соответствующей номинальному или иному определенному значению регулируемой переменной.
· Рассмотрим систему управления с единичной отрицательной обратной связью, структурная схема которой показана на рис. 3.

Рис. 3.Схема с единичной отрицательной обратной связью.
На вход системы поступает ступенчатый сигнал, на выходе можно наблюдать реакцию системы, кроме того, в качестве переходного процесса может рассматриваться изменение ошибки регулирования –
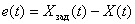 . .
Примерные графики изменения сигнала на выходе и ошибки регулирования показаны соответственно на рис. 4 и 5.
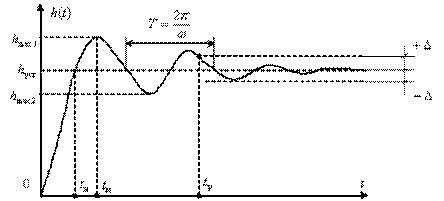
Рис. 4.Вид возможной переходной функции процесса.

Рис. 5. Вид возможной переходной функции процесса.
Рассмотрим прямые оценки качества переходных процессов, показанные на рис. 4 и 5:
1.  – минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью – – минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью –
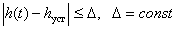 . .
 предварительно задается в процентах от установившегося значения предварительно задается в процентах от установившегося значения 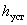 , где нет определенных требований – принимают , где нет определенных требований – принимают 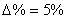 . .
2.  – перегулирование – максимальное отклонение от установившегося значения, выраженное в относительных единицах или процентах – – перегулирование – максимальное отклонение от установившегося значения, выраженное в относительных единицах или процентах –
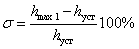 или или 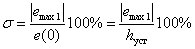 . .
Обычно требования по перегулированию составляют 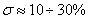 , иногда к качеству процессов может быть предъявлено требование , иногда к качеству процессов может быть предъявлено требование 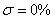 , на пример в системах позиционирования манипуляторов промышленных роботов. , на пример в системах позиционирования манипуляторов промышленных роботов.
3. 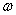 – частота колебаний – – частота колебаний –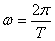 , ,
где  – период колебаний для колебательных процессов. – период колебаний для колебательных процессов.
4.  – это число полных колебаний, которое имеет – это число полных колебаний, которое имеет 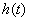 или или 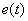 за время регулирования за время регулирования  , обычные требования по числу колебаний , обычные требования по числу колебаний 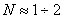 , в некоторых системах накладывают ограничение на колебательность , в некоторых системах накладывают ограничение на колебательность  , на пример, в системах с существенным люфтом в механических передачах. , на пример, в системах с существенным люфтом в механических передачах.
5. 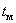 – время достижения первого максимума. – время достижения первого максимума.
6. 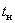 – время нарастания переходного процесса, время от начала переходного процесса до момента первого пересечения графиком линии установившегося значения. – время нарастания переходного процесса, время от начала переходного процесса до момента первого пересечения графиком линии установившегося значения.
7. 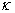 – декремент затухания, равный отношению модулей двух смежных перегулирований – – декремент затухания, равный отношению модулей двух смежных перегулирований –
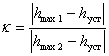 . .
Перечисленные выше показатели могут быть дополнены и другими, если этого требуют специфические технические задания на разработку или исследование систем управления.
Устойчивые переходные процессы, возникающие при ступенчатом воздействии, принято делить на три группы:
1. Монотонные процессы. Такие процессы, где первая производная выходной величины по времени не меняет знак.
2. Апериодические процессы. Здесь производная меняет знак не более одного раза.
3. Колебательные процессы. Производная меняет свой знак периодически
На рис. 6 показан примерный вид колебательного, апериодического и монотонного процессов.
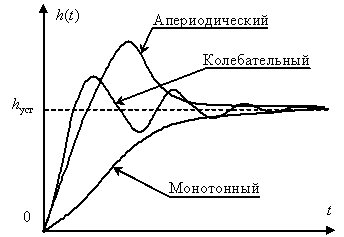
Рис. 6.Оценка вида процессов по переходной функции.
3. 3адания на практическую работу.
3.1. Произвести анализ переходного процесса по виду и устойчивости.
3.2. Оценить характер переходного процесса.
3.3. Оценить количественные характеристики переходного процесса.
4. Варианты заданий на практическую работу.
Вариант 1.
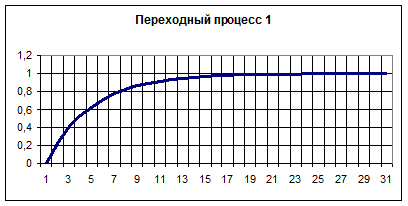  
Вариант 2.


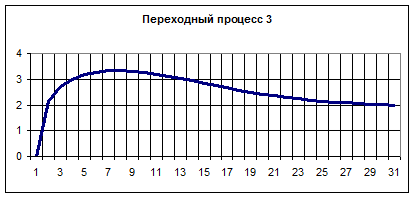
Вариант 3.
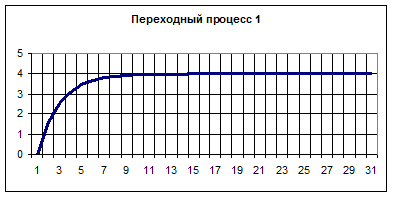 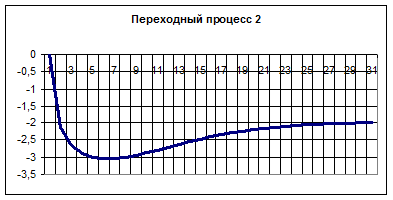 
Вариант 4.
 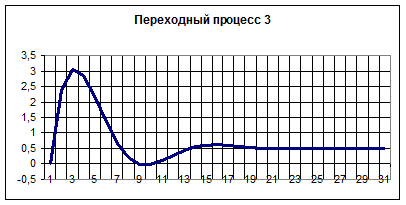 
Вариант 5.



Вариант 6.



Вариант 7.



Вариант 8.



Вариант 9.



Вариант 10.



Вариант 11.



Вариант 12.



5. Контрольные вопросы.
1. В каких системах автоматического управления важен характер и параметры протекания переходных процессов?
2. Перечислите основные области применения критериев качества.
3. Какие показатели качества относят к прямым показателям?
4. Какие показатели (критерии) качества относят к косвенным критериям?
5. Как определить время регулирования по графику переходного процесса?
6. Как определить перегулирование по графику переходного процесса?
7. Как определить время нарастания по графику переходного процесса?
8. Какие переходные процессы относят к апериодическим процессам?
9. Какие переходные процессы относят к монотонным процессам?
Практическая работа №3. «Построение временных характеристик типовых динамических звеньев».
1. Цель работы:
1.1. Научиться строить временные характеристики типовых динамических звеньев.
1.2. Научиться производить расчет передаточной функции одноконтурной САУ.
2. Общие сведения.
В теории автоматического управления рассматривают и используют следующие частотные характеристики динамических звеньев:
1. Амплитудно-частотная характеристика (АЧХ) –
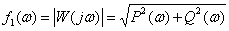 . .
2. Фазочастотная характеристика (ФЧХ) –
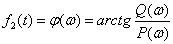 . .
3. Вещественная частотная характеристика (ВЧХ) –
 . .
4. Мнимая частотная характеристика (МЧХ) –
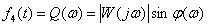 . .
5. Амплитудно-фазовая частотная характеристика (АФЧХ), которая определяется как годограф (след движения конца) вектора 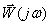 , построенный на комплексной плоскости при изменении частоты от 0 до , построенный на комплексной плоскости при изменении частоты от 0 до 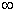 . .
На рис. 1 покажем частотные характеристики некоторого динамического звена.

Рис. 1. Частотные характеристики некоторого динамического звена.
3. Задание на практическую работу.
3.1. Для типовых элементарных динамических звеньев, заданных передаточными функциями, произвести расчет:
- амплитудно-частотной характеристики;
- фазо-частотной характеристики;
- комплексно-частотной характристики.
Результаты представить в виде графиков.
3.2. Произвести расчет переходной функции звена h(t). Поочередно изменить каждый из параметров звена, оценить его влияние на переходную функцию.
3.3. Соединить указанные звенья по указанной схеме, произвести расчет частотных характеристик соединения.
Передаточные функции звеньев:
1) Пропорциональное безинерционное звено 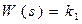
2) Интегрирующее звено 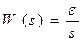
3) Апериодическое звено 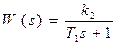
4) Дифференцирующее звено 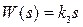
5) Реальное дифференцирующее звено 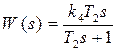
6) Звено чистого запаздывания 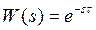
7) Звено 2-го порядка 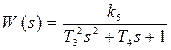
Схемы соединения:
 1) 1)
2)
- Варианты заданий на практическую работу.
| № варианта
|
k1
|
e
|
k2
|
T1
|
k3
|
k4
|
T2
|
τ
|
T3
|
T4
|
Схема
|
Блоки
|
| 1
|
1
|
0,5
|
20
|
5
|
0,05
|
2
|
80
|
3
|
1
|
2
|
1
|
1,2,3
|
| 2
|
2
|
1,5
|
19
|
10
|
0,1
|
4
|
75
|
6
|
2
|
3
|
2
|
3,4,1
|
| 3
|
3
|
2,5
|
18
|
15
|
0,15
|
6
|
70
|
9
|
3
|
9
|
1
|
3,5,6
|
| 4
|
4
|
3,5
|
17
|
20
|
0,2
|
8
|
65
|
12
|
4
|
8
|
2
|
2,3,1
|
| 5
|
5
|
4,5
|
16
|
25
|
0,25
|
10
|
60
|
15
|
5
|
3
|
1
|
2,4,1
|
| 6
|
6
|
5,5
|
15
|
30
|
0,3
|
12
|
55
|
18
|
6
|
15
|
2
|
3,4,2
|
| 7
|
7
|
6,5
|
14
|
35
|
0,35
|
14
|
50
|
21
|
7
|
14
|
1
|
1,2,3
|
| 8
|
8
|
7,5
|
13
|
40
|
0,4
|
16
|
45
|
24
|
8
|
2
|
2
|
3,4,1
|
| 9
|
9
|
8,5
|
12
|
45
|
0,45
|
18
|
40
|
27
|
9
|
24
|
1
|
3,5,6
|
| 10
|
10
|
9,5
|
11
|
50
|
0,5
|
20
|
35
|
30
|
10
|
20
|
2
|
2,3,1
|
| 11
|
11
|
10,5
|
10
|
55
|
0,55
|
22
|
30
|
33
|
11
|
5
|
1
|
2,4,1
|
| 12
|
12
|
11,5
|
9
|
60
|
0,6
|
24
|
25
|
36
|
12
|
30
|
2
|
3,4,2
|
5. Контрольные вопросы.
1.Как рассчитывается Амплитудно-Частотная Характеристика?
2.Что называют Фазо-Частотной Характеристикой?
3.Привести передаточные функции типовых динамических звеньев.
4.Как рассчитывается передаточная функция одноконтурной системы охваченной единичной обратной связью?
5.Приведите передаточные функции параллельного и последовательного соединения звеньев?
Практическая работа №4. «Преобразование структурных схем».
1. Цель работы:
1.1. Научиться строить структурные схемы АСР.
1.2. Изучить основные приемы преобразования структурных схем.
2. Общие сведения.
При преобразовании сложных структурных схем к более простому виду, часто приходиться переносить точки ветвления по направлению прохождения сигнала и против него, а также перенос элементов суммирования.
Рассмотрим эти случаи по отдельности.
Если осуществляется перенос точки ветвления против направления прохождения сигнала, то в переносимую ветвь нужно включить передаточные функции элементов встречающихся на пути прохождения сигнала между прежней и новой точкой ветвления (рис.1).
 . .
Если осуществляется перенос точки ветвления по направлению прохождения сигнала, то в переносимую ветвь нужно включить обратные передаточные функции элементов встречающихся на пути прохождения сигнала между прежней и новой точкой ветвления (рис.2).
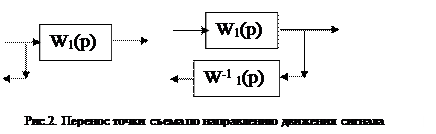
Если осуществляется перенос сумматора по направлению прохождения сигнала, то в переносимую ветвь нужно включить передаточные функции элементов встречающихся на пути прохождения сигнала между прежней и новой точкой ветвления (рис.3).

3. Задание на практическую работу.
3.1. Математическая модель объекта, имеющего один вход и один выход, задана в виде дифференциального уравнения вида:
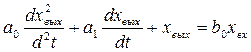
где 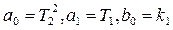
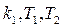 - коэффициент усиления и постоянные времени соответственно. - коэффициент усиления и постоянные времени соответственно.
Преобразовать эту модель в структурную схему, представляющую собой соединение двух типовых элементарных звеньев с обратной связью.
Построить КЧХ системы, используя варианты заданий.
3.2. Найти передаточную функцию замкнутой системы изображенной на рис. 4, предварительно преобразовав ее к простому виду с помощью правил структурного преобразования.

4. Варианты заданий на практическую работу.
Использовать таблицу вариантов практической работы №3.
5. Контрольные вопросы.
1. Как осуществляется перенос точки ветвления против направления движения сигнала?
2. Как осуществляется перенос точки ветвления по направлению движения сигнала?
3. Как осуществляется перенос сумматора?
Практическая работа №5. «Устойчивость линейных систем».
1. Цель работы:
1.1. Изучить алгебраические критерии устойчивости.
1.2. Изучить частотные критерии устойчивости.
2. Общие сведения.
Критериями устойчивости называют признаки, позволяющие определить знак корней характеристического уравнения, то есть решить вопрос устойчивости, не находя самих корней.
Существуют следующие критерии устойчивости линейных систем:
1) Алгебраические критерии устойчивости:
- критерий Гурвица;
- критерий Рауса;
- критерий Вышнеградского.
2) Частотные критерии устойчивости:
- критерий Найквиста;
- критерий Михайлова.
Критерий Гурвица.
Составляем характеристическое уравнение системы, а0
> 0
a0
sn
+ a1
sn-1
+ … + an-1
s + an
= 0
Затем составляем систему определителей:
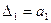   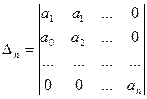
Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы при а0 > 0 все определители Гурвица были больше нуля:
Следствием будет являться необходимое условие устойчивости:
ai
> 0 – коэффициенты характеристического уравнения
Отрицательность коэффициентов однозначно указывает на неустойчивость системы.
Критерий Михайлова.
Характеристическое уравнение системы, а0
> 0
a0
sn
+ a1
sn-1
+ … + an-1
s + an
= 0
Составляется вектор Михайлова:
M(jω) = a0
(jω) n
+ a1
(jω) n-1
+ … + an
= U(ω) + j V(ω)
Система будет устойчивой, если годограф Михайлова (рис. 2), начинаясь с положительной вещественной полуоси будет описан вектором, вращающимся в положительном направлении, нигде не обращающемся в нуль и последовательно проходящем n квадрантов, где n – степень характеристического уравнения.
Критерий Найквиста.
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по КЧХ разомкнутой системы
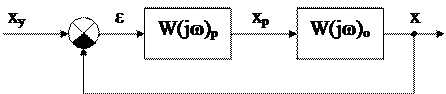
Рис. 1. Структурная схема замкнутой системы с обратной связью.
Строится КЧХ разомкнутой системы. Если разомкнутая система устойчива или нейтральна и ее КЧХ при изменении частоты

Рис.2. Годограф Михайлова.
от 0 до ¥ не охватывает в комплексной плоскости точку (-1; j0), то замкнутая система устойчива.
Охватываемой областью считается область, лежащая справа от КЧХ при движении по ней в сторону увеличения частоты. Это область замкнута при рассмотрении -¥ < ω < ¥.
3. Задание на практическую работу.
1. Характеристическое уравнение системы имеет вид:
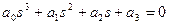
Определить устойчивость этой системы, используя критерий Гурвица.

Рис.3. КЧХ разомкнутой системы.
2. Передаточная функция разомкнутой системы имеет вид:
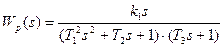
Определить устойчивость замкнутой системы, используя критерий Гурвица.
3. Используя в качестве передаточной функции разомкнутой системы последовательное соединение звеньев указанных для вашего варианта в таблице практической работе №3 рассчитать с помощью критерия Михайлова коэффициент усиления замкнутой системы, при котором замкнутая система будет находиться на границе устойчивости.
4. Используя условия предыдущего задания с помощью критерия Найквиста определить интервалы общего коэффициента усиления замкнутой системы при которых: а) система устойчива; б) находится на границе устойчивости; в) система не устойчива.
4. Варианты заданий на практическую работу.
| №
варианта
|
a0
|
a1
|
a2
|
a3
|
k1
|
T1
|
T2
|
T3
|
| 1
|
2
|
0.5
|
1
|
0.2
|
1
|
1
|
2
|
2
|
| 2
|
0.22
|
0.8
|
1.2
|
0.4
|
0.2
|
2
|
1.5
|
4
|
| 3
|
0.82
|
1.8
|
0.6
|
0.74
|
0.8
|
3
|
5
|
1
|
| 4
|
2
|
3
|
1
|
0.5
|
1.2
|
4
|
0.8
|
1.5
|
| 5
|
1
|
1
|
2
|
1
|
1
|
3
|
1.3
|
3
|
| 6
|
0.83
|
0.2
|
1.5
|
0.58
|
0.7
|
1
|
1
|
1
|
| 7
|
0.46
|
0.9
|
1.12
|
1.94
|
0.6
|
2
|
1.7
|
2
|
| 8
|
1.5
|
2
|
1
|
3.5
|
1.3
|
5
|
2
|
4
|
| 9
|
4
|
5
|
1
|
2
|
1.1
|
7
|
5
|
3
|
| 10
|
2
|
14.5
|
0.95
|
2.5
|
0.9
|
4
|
1.8
|
1
|
| 11
|
2
|
5
|
2
|
4
|
2
|
2
|
0.9
|
2
|
| 12
|
1
|
6
|
3
|
2
|
1.7
|
3
|
2
|
1.5
|
5. Контрольные вопросы.
1. Сформулируйте критерий Гурвица.
2. Устойчивость каких систем возможно определить с помощью критериев Михайлова и Найквиста?
Практическая работа №6. «Построение переходных процессов. Расчет настроек регулятора».
1. Цель работы:
1.1. Изучить построение переходного процесса с методом Акульшина.
1.2. Научиться рассчитывать настроечные параметры регуляторов.
2. Общие сведения.
2.1. Метод Акульшина относится к приближенным методам построения переходных процессов и позволяет находить вид переходного процесса под воздействием ступенчатых входных сигналов (рис. 1).
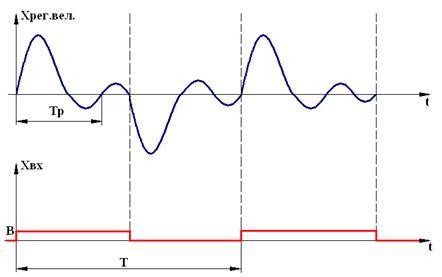
Рис.1. Построение переходного процесса.
При этом должно выполняться следующее условие: 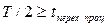
Входной сигнал преобразуется в ряд Фурье для прямоугольной волны вида:
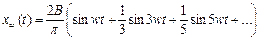
где 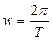 . .
Затем строиться годограф замкнутой системы: 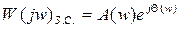 . .
Далее оцениваем влияние, оказываемое каждой гармоникой, для этого разложим хрег
в ряд:
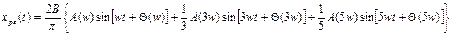 По принципу суперпозиции реакция системы на сумму входных воздействий равна сумме реакций на каждое входной воздействие. Оценивается воздействие каждой гармоники входного сигнала По принципу суперпозиции реакция системы на сумму входных воздействий равна сумме реакций на каждое входной воздействие. Оценивается воздействие каждой гармоники входного сигнала
При практически используемых степенях затухания переходных процессов, он затухает не более, чем за три рабочих периода Тр
.
Тогда Т=6Тр
, 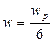
Рабочую частоту находят, как показано на рис. 2. Для этого необходимо построить АЧХ замкнутой системы.
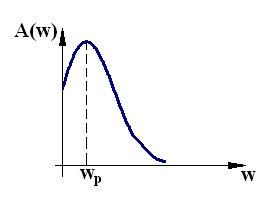
Рис. 2. Построение АЧХ системы.
Затем в интервале 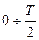 строят переходной процесс. Достаточная точность при этом достигается при строят переходной процесс. Достаточная точность при этом достигается при 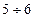 гармониках хвх
. гармониках хвх
.
2.2. Алгоритм функционирования регулятора (закон регулирования) – уравнение, устанавливающее связь между входными и выходными величинами.

Рис. 3. Структурная схема регулятора.
Классификация регуляторов:
- астатические и статические
- прямого и непрямого действия
- с корректирующими элементами и без них
- с постоянной или пропорциональной скоростью сервомотора
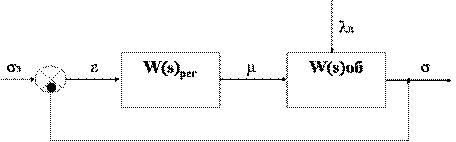
Рис. 4. Структурная схема.
При автоматизации технологических процессов важнейшей является задача стабилизации выходных координат объектов регулирования. Для этого в основном используются одноконтурные системы регулирования, состоящие из объекта и регулятора (рис. 4).
При этом необходимо обеспечить системе определенный запас устойчивости и удовлетворительное качество переходных процессов. Реализовать это возможно с помощью расчета настроечных параметров регуляторов. Методов и алгоритмов расчета последних существует большое количество, однако условно их можно разделить на две группы. Первая – расчет оптимальных параметров настройки, сопряженные с выполнением значительного объема вычислительных процедур. И вторая, позволяющая рассчитать приближенные параметры.
Два наиболее характерных метода:
- метод расширенных амплитудно-частотных характеристик;
- метод незатухающих колебаний.
Рассмотрим типовые промышленные регуляторы.
Интегральный (И-регулятор).
Передаточные функции И-регулятора: 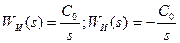
И-регулятор имеет один настроечный параметр – С0
.
С увеличением С0
увеличивается время переходного процесса и уменьшаются динамические ошибки
Пропорциональный (П-регулятор)
Передаточная функция WП
(s) = С1
П-регулятор имеет один настроечный параметр – С1
.
Пропорционально-интегральный регулятор (ПИ-регулятор).
Передаточная функция ПИ-регулятора: 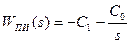
Пропорционально-интегрально-дифференциальный регулятор (ПИД-регулятор).
Передаточная функция ПИ-регулятора:
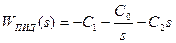
Рассмотрим метод незатухающих колебаний. Определение настроек регулятора производится в два этапа. На первом определяется критическая частота 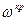 и критическая настройка П-регулятора и критическая настройка П-регулятора 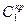 , при которой в замкнутой САР возникают незатухающие колебания. На втором – определение по , при которой в замкнутой САР возникают незатухающие колебания. На втором – определение по 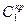 настроечных параметров регуляторов по приближенным формулам. настроечных параметров регуляторов по приближенным формулам.
Определение 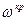 и и 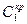 . .
Если разомкнутая система устойчива (или нейтральна) и ее АФХ проходит через точку (1, j0), то замкнутая САР будет находиться на границе устойчивости. Условие нахождения системы на границе устойчивости, имеет вид:
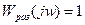
или, учитывая, что 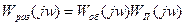 , получаем , получаем
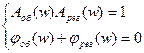
где  - амплитудно-частотная характеристика и фазо-частотная характеристика характеристика объекта и регулятора соответственно. - амплитудно-частотная характеристика и фазо-частотная характеристика характеристика объекта и регулятора соответственно.
Поскольку АФХ П-регулятора имеет вид

тогда для расчета критической частоты 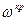 и критической настройки П-регулятора и критической настройки П-регулятора 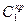 получим два уравнения: получим два уравнения:
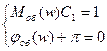
Из второго уравнения находится значение 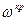 , затем из первого по формуле: , затем из первого по формуле:
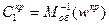
Определение настроек регуляторов. Расчет настроек регуляторов по 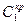 и и 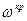 осуществляется по приближенным формулам. осуществляется по приближенным формулам.
Для П-регулятора:
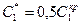
Для ПИ-регулятора:

Ткр
– период незатухающих колебаний САР.
Для ПИД-регулятора:

где Тиз
, Тпр
– время изодрома и предварения.
Приближенные формулы определяют настройки регуляторов, обеспечивающие степень затухания процесса регулирования более чем 0,75.
Приближенные настройки регулятора можно найти по параметрам динамики объекта: времени запаздывания t, постоянной времени Т и коэффициента усиления k.
П-регулятор.
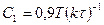
ПИ-регулятор.
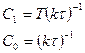
ПИД-регулятор.
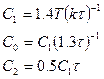
Приближенные формулы определяют настройки регуляторов, обеспечивающие степень затухания процесса регулирования более чем 0,75.
3. Задание на практическую работу.
3.1. Для типовых элементарных динамических звеньев, заданных передаточными функциями, произвести построение переходного процесса при ступенчатом единичном воздействии методом Акульшина. Оценить погрешность по сравнению с точным решением дифференциального уравнения. Параметры звеньев указаны в таблице.
Передаточные функции звеньев:
1) Апериодическое звено 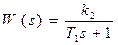
2) Реальное дифференцирующее звено 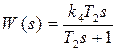
3) Звено 2-го порядка 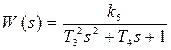
3.2. Динамические свойства объекта заданы дифференциальным уравнением вида:
a0
xвых
’’’
+ a1
xвых
’’
+ a2
xвых
’
+ a3
xвых
= b0
xвх
Коэффициенты уравнения указаны в таблице. Рассчитать приближенные настроечные параметры П-,ПИ-,ПИД-регуляторов методом незутухающих колебаний. Для указанного регулятора методом Акульшина построить переходный процесс в замкнутой системе по управляющему воздействию. Оценить качество переходного процесса и сравнить с заданным.
4. Варианты заданий на практическую работу.
| №
|
k2
|
T1
|
k4
|
T2
|
T3
|
T4
|
k5
|
m
|
Регу-лятор
|
| 1
|
20
|
5
|
2
|
80
|
1
|
2
|
10
|
0,221
|
И
|
| 2
|
19
|
10
|
4
|
75
|
2
|
3
|
9
|
0,227
|
П
|
| 3
|
18
|
15
|
6
|
70
|
3
|
9
|
8
|
0,233
|
ПИ
|
| 4
|
17
|
20
|
8
|
65
|
4
|
8
|
7
|
0,239
|
И
|
| 5
|
16
|
25
|
10
|
60
|
5
|
3
|
6
|
0,245
|
П
|
| 6
|
15
|
30
|
12
|
55
|
6
|
15
|
5
|
0,251
|
ПИ
|
| 7
|
14
|
35
|
14
|
50
|
7
|
14
|
4
|
0,257
|
И
|
| 8
|
13
|
40
|
16
|
45
|
8
|
2
|
3
|
0,263
|
П
|
| 9
|
12
|
45
|
18
|
40
|
9
|
24
|
2
|
0,269
|
ПИ
|
| 10
|
11
|
50
|
20
|
35
|
10
|
20
|
1
|
0,275
|
И
|
| 11
|
10
|
55
|
22
|
30
|
11
|
5
|
20
|
0,281
|
П
|
| 12
|
9
|
60
|
24
|
25
|
12
|
30
|
19
|
0,287
|
ПИ
|
| а0
|
а1
|
а2
|
а3
|
в0
|
| 4
|
10
|
6
|
2
|
4
|
| 8
|
20
|
8
|
8
|
6
|
| 5
|
15
|
10
|
12
|
8
|
| 2
|
25
|
12
|
22
|
10
|
| 9
|
35
|
14
|
14
|
12
|
| 3
|
30
|
16
|
10
|
14
|
| 7
|
15
|
14
|
8
|
16
|
| 2
|
20
|
12
|
12
|
18
|
| 8
|
45
|
10
|
18
|
20
|
| 9
|
15
|
8
|
20
|
22
|
| 3
|
75
|
6
|
10
|
24
|
| 6
|
35
|
4
|
8
|
26
|
5. Контрольные вопросы.
1. Для чего применяется метод Акульшина?
2. В чем заключается сущность метода Акульшина?
3. Как рассчитывается рабочая частота?
4. Приведите передаточные функции И-регулятора.
5. Приведите передаточные функции ПИ-регулятора.
6. Приведите передаточные функции ПИД-регулятора.
7. Как осуществляется расчет настроек регулятора методом незатухающих колебаний?
8. Как осуществляется расчет настроек регулятора по параметрам динамики объекта?
Список рекомендованной литературы.
1.
Воронов А.А. (ред). Теория автоматического управления, части 1 и 2. М.: Высшая школа, 1986.
2.
Нетушил А.В. (ред). Теория автоматического управления. М.: Высшая школа, 1976.
3.
Шаталов А.С. (ред.). Теория автоматического управления. М.: Высшая школа, 1977
4.
Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. М.: Наука, 1974.
5.
Иванов В.А., Чемоданов В.К., Медведев В.С. Математические основы теории автоматического регулирования.М.: Высшая школа, 1973.
6.
Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Высшая школа, 1989.
7.
Воронов А.А. Устойчивость, управляемость, наблюдаемость. М.: Наука, 1979.
8.
Первозванский А.А. Курс теории автоматического управления. М.: Высшая школа, 1986.
9.
Бесекерский В.А. (ред). Сборник задач по теории автоматического регулирования и управления. М.: Наука, 1978.
10.
Шаталов А.С. (ред.) Задачник по теории автоматического управления. М.: Энергия, 1979.
АГТУ зак. тираж
|