| УРАВНЕНИЕ СОСТОЯНИЯ КРОВИ ПРИ ТЕЧЕНИИ
В МЕЛКИХ СОСУДАХ
А.Е. Медведев
Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
630090, Новосибирск,
e-
mail:
medvedev@
itam.
nsc.
ru
Введение.
Течение крови имеет ряд особенностей – в крупных кровеносных сосудах (более 1000 микрон) кровь ведет себя как ньютоновская вязкая несжимаемая жидкость, для более мелких сосудов необходимо учитывать реологические неньютоновские свойства течения крови [1]. Поэтому для математического описания течения крови в крупных сосудах обычно используется модель вязкой несжимаемой ньютоновской жидкости, а для мелких кровеносных сосудов – различные реологические модели неньютоновской жидкости.
Особенности течения крови.
Кровь (с точки зрения механики) представляет собой суспензию, состоящую из плазмы (вязкая несжимаемая жидкость) и эритроцитов (двояковогнутые деформируемые диски размером 8 мкм на 2.5 мкм, заполненные гелем). Одной из основных характеристик крови является показатель гематокрита 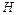 – объемное содержание эритроцитов в крови. Течение крови в сосудах отличается особенностями (эффектами): I) зависимость показателя гематокрита от диаметра сосуда (эффект Фареуса); II) существование пристеночного слоя плазмы без эритроцитов; III) тупой (по сравнению с профилем течения Пуазейля) профиль скорости крови; IV) вязкость крови падает с уменьшением размера сосуда (эффект Фареуса-Линдквиста. – объемное содержание эритроцитов в крови. Течение крови в сосудах отличается особенностями (эффектами): I) зависимость показателя гематокрита от диаметра сосуда (эффект Фареуса); II) существование пристеночного слоя плазмы без эритроцитов; III) тупой (по сравнению с профилем течения Пуазейля) профиль скорости крови; IV) вязкость крови падает с уменьшением размера сосуда (эффект Фареуса-Линдквиста.
Модель течения крови.
Рассмотрим кровь как суспензию, состоящую из двух несжимаемых фаз. Первая фаза – плазма крови, вторая – эритроциты. Относительная вязкость суспензии зависит от концентрации и, согласно формуле Эйнштейна, имеет вид
 (1) (1)
где 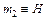 – объемная доля эритроцитов (локальный показатель гематокрита), – объемная доля эритроцитов (локальный показатель гематокрита), 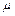 , , 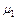 – динамическая вязкость крови и плазмы, соответственно. – динамическая вязкость крови и плазмы, соответственно.
Известно ([2]), что эритроциты неравномерно распределены по сечению сосуда, то есть объемная доля эритроцитов 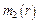 зависит от радиуса. Решение уравнений, аналогичных уравнениям Пуазейля, но с переменной вязкостью, дает скорость крови зависит от радиуса. Решение уравнений, аналогичных уравнениям Пуазейля, но с переменной вязкостью, дает скорость крови
 (2) (2)
где 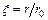 – безразмерный радиус, – безразмерный радиус, 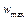 – максимальная скорость течения Пуазейля. – максимальная скорость течения Пуазейля.
Скорость крови 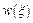 имеет более тупой профиль, по сравнению с параболическим решением Пуазейля имеет более тупой профиль, по сравнению с параболическим решением Пуазейля  . Это связано с тем, что концентрация эритроцитов . Это связано с тем, что концентрация эритроцитов 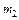 имеет максимум на оси сосуда и минимум на стенке. В силу этого относительная вязкость имеет максимум на оси сосуда и минимум на стенке. В силу этого относительная вязкость 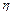 (1) имеет максимум на оси и минимум на стенке сосуда. Тогда в центре сосуда (при (1) имеет максимум на оси и минимум на стенке сосуда. Тогда в центре сосуда (при 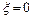 ) имеем ) имеем  , отсюда получим , отсюда получим  ; на стенке сосуда (при ; на стенке сосуда (при 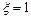 ) скорость течения крови ) скорость течения крови  . Таким образом, профиль скорости течения крови тупой, по сравнению с профилем скорости Пуазейля. . Таким образом, профиль скорости течения крови тупой, по сравнению с профилем скорости Пуазейля.
Для простоты примем, что распределение объемной доля эритроцитов 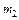 по сечению сосуда задается ступенчатой функцией: по сечению сосуда задается ступенчатой функцией:
 (5) (5)
где 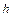 – относительная толщина пристеночного слоя плазмы, – относительная толщина пристеночного слоя плазмы, 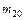 – объемная доля эритроцитов на оси сосуда. – объемная доля эритроцитов на оси сосуда.
Эффект образования пристеночного слоя связан с поперечной миграцией эритроцитов при движении по сосуду. В механике суспензий это явление называется эффектом Сегре-Зильберберга. Толщина пристеночного слоя зависит от диаметра трубы, свойств несущей жидкости и частиц. Поведение эритроцитов во время движения кардинально отличается от твердых частиц – эритроциты могут деформироваться и слипаться, образую “монетные столбики”. Для нахождения уравнения состояния крови были взяты экспериментальные данные по зависимости показателя гематокрита от диаметра сосуда (рис. 1a
).
Задача нахождения уравнения состояния крови сводится к решению алгебраического уравнения на толщину пристеночного слоя 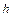 и объемной доли эритроцитов и объемной доли эритроцитов 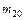 : :
 (5) (5)
где  , ,  – функция, аппроксимирующая экспериментальные данные на рис. 1a
. – функция, аппроксимирующая экспериментальные данные на рис. 1a
.
Выводы.
Проведено сравнение с известными экспериментальными данными [1-3] по относительной наблюдаемой вязкости 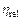 (рис. 1a
), по толщине пристеночного слоя (рис. 1a
), по толщине пристеночного слоя 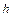 (рис. 2a
) и профилю продольной скорости крови (рис. 2a
) и профилю продольной скорости крови 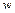 (рис. 2b
). Как видно из рис. 1 и 2, несмотря на грубое приближение профиля локального гематокрита ступенчатой функцией (5), результаты расчета по модели находятся в рамках погрешности экспериментальных измерений. (рис. 2b
). Как видно из рис. 1 и 2, несмотря на грубое приближение профиля локального гематокрита ступенчатой функцией (5), результаты расчета по модели находятся в рамках погрешности экспериментальных измерений.
Получена зависимость вязкости крови от диаметра сосуда для описания течения в сосудах диаметра больше 4.5 микрон. Данные зависимости имеют единые вид для сосудов всех размеров и переходят в формулы течения Пуазейля при больших диаметрах сосудов.
Работа выполнена при поддержке междисциплинарного интеграционного проекта СО РАН № 91.
СПИСОК ЛИТЕРАТУРЫ
1.
Левтов В.А., Регирер С.А., Шадрина Н.Х.
Реология крови. М.: Медицина, 1982. 272 с.
2.
Pries A.R., Secomb T.W.
In: Handbook of Physiology: Microcirculation. Ed. Tuma R.F., Dura W.N., Ley K. 2nd
ed. Academ Press. 2008. P. 3–36.
3.
Sharan M., Popel A.S.
A two-phase model for flow of blood in narrow tubes with increased effective viscosity near the wall // Biorheology. 2001. V. 38. P. 415–428.
4.
Long D.S., Smith M.L., Pries A.R. et al.
Microviscometry reveals reduced blood viscosity and altered shear rate and shear stress profiles in microvessels after hemodilution // Proc. Natl. Acad. Sci. USA. 2004. V. 101. N. 27. P. 10060–10065.
|