| УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ. ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ
СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 2
1. Уравнение в полных дифференциалах. 3
2. Интегрирующий множитель. 5
ЗАКЛЮЧЕНИЕ. 8
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.. 10
ВВЕДЕНИЕ
Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины.
Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. Большое значение, которое имеют дифференциальные уравнения для математики и, особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач.
Дифференциальное уравнение является основой математического моделирования. Дифференциальным уравнением называется соотношение между функциями и их производными. Если функции одной переменной, то имеем обыкновенные дифференциальные уравнения, если функции нескольких переменных, то дифференциальное уравнение в частных производных[1]
.
Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).
1. Уравнение в полных дифференциалах.
Пусть уравнение вида f(t, x)dx + g(t,x)dt = 0, F
(t, x) = C является уравнением в полных дифференциалах
, т. е. существует такая дифференцируемая функция F
(t, x), что
dF
(t, x) = f(t, x)dx + g(t, x)dt ((t, x) О D
(f) = D
(g)).
Тогда следующее уравнение является его полным интегралом:
F
(t
, x
) = C
(t
, x
Î D
1
).
Доказательство. Пусть функции t
= y(s
), x
= j(s
) определены на некотором промежутке J
Ì R
. Тот факт, что пара (y, j) есть решение уравнения f(t, x)dx + g(t,x)dt = 0, F
(t, x) = C эквивалентен тождеству
[f
(t
, x
)dx
+ g
(t
, x
)dt
]|t
=
y
, dt
=
y¢
ds
, x
=
j
, dx
=
j¢
ds
º 0,
которое, в свою очередь эквивалентно тождеству
[d
F(t
, x
)]|t
=
y
, dt
=
y¢
ds
, x
=
j
, dx
=
j¢
ds
º 0.
Последнее в точности означает, что
d
[F(t
, x
)]|t
=
y
, x
=
j
º 0 и y, j Î D
1
,
или, что, то же,
F[y(s
), j(s
)] º C
и y, j Î D
1
.
Таким образом, f(t, x)dx + g(t,x)dt = 0, F
(t, x) = C
Û F(t
, x
) = C
(t
, x
Î D
1
).
Для уравнения с разделяющимися переменными f
(x
)dx
– g
(t
)dt
= 0 существует функция F(t
, x
) = F
(x
) – G
(t
), дифференциал которой совпадает с левой частью этого уравнения. Следовательно, это есть частный случай уравнения в полных дифференциалах.
Обобщенное утверждение об уравнении в полных дифференциалах
[2]
. Пусть в уравнении
f
1
(x
)dx
1
+ f
2
(x
)dx
2
+ ... + fn
(x
)dxn
= 0
функции fi
(x) = fi
(x1
, ..., xn
) непрерывны вместе со своими частными производными ¶fi
/¶xk
(i ¹ k) на декартовом произведении интервалов J1
× J2
×... × Jn
= D.
Тогда левая часть уравнения f
1
(x
)dx
1
+ f
2
(x
)dx
2
+ ... + fn
(x
)dxn
= 0 будет полным дифференциалом некоторой функции F(x) в том и только том случае, если
| ¶Fi
¶xk
|
=
|
¶Fk
¶xi
|
(i
, k
= 1, 2, ..., n
; i
¹ k
; x
Î D).
|
При этом функция F находится по формуле
| F(x
) =
|
n
å
k
= 1
|
ò
|
xk
x
0
k
|
f
(x
1
, ..., xk
–1
, x, x
0
k
+1
, ..., x
0
n
) d
x
|
(x0
k
Î Jk
— произвольные фиксированные точки), а полный интеграл уравнения f
1
(x
)dx
1
+ f
2
(x
)dx
2
+ ... + fn
(x
)dxn
= 0 можно записать в виде:
F(x
) = C
(x
Î D
1
).
В частности, условиям данной теоремы удовлетворяет уравнение с разделенными переменными
f
1
(x
1
)dx
1
+ f
2
(x
2
)dx
2
+ ... + fn
(xn
)dxn
= 0,
если функции fk
: Jk
® R
непрерывны; полный интеграл имеет вид
F
1
(x
1
) + F
2
(x
2
) + ... + Fn
(xn
) = 0,
где Fk
–первообразная fk
(k
= 1, ..., n
).
2. Интегрирующий множитель.
Итак, если для уравнения f(t, x)dx + g(t,x)dt = 0, F
(t, x) = C условие полного дифференциала (необходимый признак уравнения в полных дифференциалах:
| ¶f
¶t
|
=
|
¶g
¶x
|
((t
, x
) Î J
1
×J
2
).
|
не выполнено, то иногда удается найти функцию m = m(t
, x
), такую, что для уравнения
m · f
(t
, x
)dx
+ m · g
(t
, x
)dt
= 0
оно уже выполнено. В этом случае функция m называется интегрирующим множителем
. Общего способа нахождения интегрирующего множителя не существует, однако можно указать простые признаки существования и прием построения интегрирующих множителей, зависящих только от x или только от t.
Если, например, считать, что m зависит только от x, то
| ¶m · f
¶t
|
= m
|
¶f
¶t
|
=
|
¶m · g
¶x
|
= m¢ + m
|
¶g
¶x
|
,
|
и аналог условия
| ¶f
¶t
|
=
|
¶g
¶x
|
((t
, x
) Î J
1
×J
2
).
|
для m · f
(t
, x
)dx
+ m · g
(t
, x
)dt
= 0 выглядит так:
| m¢ =
|
é
ê
ë
|
æ
ç
è
|
¶f
¶t
|
–
|
¶g
¶x
|
ö
÷
ø
|
/
|
g
|
ù
ú
û
|
· m.
|
Если выражение в квадратных скобках не зависит от t
, то
| m¢ =
|
é
ê
ë
|
æ
ç
è
|
¶f
¶t
|
–
|
¶g
¶x
|
ö
÷
ø
|
/
|
g
|
ù
ú
û
|
· m.
|
есть линейное однородное уравнение относительно m = m(x
); оно легко решается и дает интегрирующий множитель для f(t, x)dx + g(t,x)dt = 0, F
(t, x) = C .
Аналогично ищется интегрирующий множитель, зависящий только от t
.
Найдем интегрирующий множитель m = m(x
) для уравнения
(3t
2
/x
2
– 1)dt
+ (3 – 2t
/x
)dx
= 0
(оно получено почленным делением уравнения (3t
2
– x
2
)dt
+ (3x
2
– 2tx
)dx
= 0 на x
2
, поэтому мы заранее знаем, что интегрирующий множитель m = x
2
существует). Выпишем для уравнения (3t
2
/x
2
– 1)dt
+ (3 – 2t
/x
)dx
= 0, умноженного почленно на m, условие полного дифференциала:
| ¶m · (3 – 2t
/x
)
¶t
|
= m ·
|
æ
ç
è
|
–
|
2
x
|
ö
÷
ø
|
;
|
| ¶m · (3t
2
/x
2
– 1)
¶x
|
= m¢(3t
2
/x
2
– 1) + m ·
|
æ
ç
è
|
–
|
6t
2
x
3
|
ö
÷
ø
|
;
|
,
| m¢ =
|
é
ê
ë
|
æ
ç
è
|
–
|
2
x
|
+
|
6t
2
x
3
|
ö
÷
ø
|
/
|
(3t
2
/x
2
– 1)
|
ù
ú
û
|
· m =
|
2
x
|
m.
|
Поскольку выражение в квадратных скобках оказалось не зависящим от t
, искомый интегрирующий множитель существует и находится из уравнения:
| ¶m
m
|
=
|
2dx
x
|
; m = Cx
2
.
|
В частности, мы получили уже известный нам заранее интегрирующий множитель m = x
2
.
ЗАКЛЮЧЕНИЕ
Одним из распространенных способов изучения явлений математическими методами является моделирование этих явлений в виде дифференциальных уравнений[3]
.
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, искомую функцию и их производные.
Если искомая функция y является функцией одного аргумента x, то дифференциальное уравнение называется обыкновенным дифференциальным уравнением. Если искомая функция зависит от нескольких аргументов, то дифференциальное уравнение называется уравнением в частных производных.
Если в дифференциальном уравнении
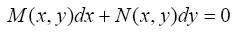
функции М
(х
, у
) и N
(x
, y
) удовлетворяют условию 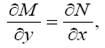 такое уравнение называется уравнением в полных дифференциалах. Смысл названия объясняется тем, что при этом существует функция U (x, y) такая, что
Тогда из уравнения
следует, что
что является общим интегралом исходного уравнения. Таким образом, задача сводится к отысканию функции U
. Ее можно найти в виде:
любые числа, входящие в область определения функций М
и N
, а  – произвольная постоянная.
Интегрирующий множитель, множитель, после умножения на который левая часть дифференциального уравнения
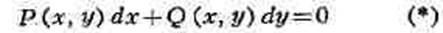
обращается в полный дифференциал (дифференциальное исчисление) некоторой функции V(x, y). T. о., если
Если 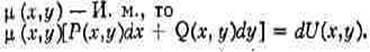 множитель мю (x,y) известен, то задача интегрирования уравнения (*) сводится к квадратурам, т. к. остаётся найти функцию U(x, y) по её полному дифференциалу[4]
.
В нашем реферате мы рассмотрели уравнение в полных дифференциалах и интегрирующий множитель.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Берман Г.Н Сборник задач по курсу математического анализа. - М.: Наука, 2005. - 384с.
2. Бибиков Ю.Р. Курс обыкновенных дифференциальных уравнений. – М.: Высшая школа, 2002. – 304 с.
3. Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальное и интегральное исчисление. – М.: Наука, 2002.
4. Бугров Я.С., Никольский С. М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 2003.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 2001, ч. I, II.
6. Задачи и упражнения по математическому анализу / Под ред. Б.П. Демидовича. - М.: Наука, 2001. - 416 с.
7. Краснов М.Л., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновенным дифференциальным уравнениям. – М., Высш. школа, 2001.
8. Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, 2002.
9. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1999. – 332 с.
10. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения:примеры и задачи. – М.: Высшая школа, 2003. – 383 с.
[1]
Бибиков Ю.Р. Курс обыкновенных дифференциальных уравнений. – М.: Высшая школа, 2002. – 304 с.
[2]
Задачи и упражнения по математическому анализу / Под ред. Б.П. Демидовича. - М.: Наука, 2001. - 416 с.
[3]
Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1999. – 332 с.
[4]
Краснов М.Л., Киселев А.И., Макаренко Г.И. Сборник задач по обыкновенным дифференциальным уравнениям. – М., Высш. школа, 2001.
|
