| ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУВПО «Самарский государственный архитектурно-строительный
университет»
Факультет информационных систем и технологий
Кафедра прикладной математики и вычислительной техники
РЕФЕРАТ
по дисциплине
«ТЕХНОЛОГИЯ/МЕТОДОЛОГИЯ НАУЧНЫХ ИССЛЕДОВАНИЙ»
на тему:
«Компьютерный анализ опытов Стокса»
III СЕМЕСТР 2 КУРС
Методический руководитель: Декан ФИСТ, д.т.н., профессор
Пиявский Семен Авраамович
Научный руководитель: Семёнов Алексей Владимирович
| Проверили:
|
Выполнила: студентка ГИП-107
Сулковская А.С.
|
| |
|
| |
|
| |
|
| |
|
Общая оценка____________________
Методический руководитель Пиявский С.А. Оценка Дата
2008 год
Содержание
1. Введение 3
2. Основная часть 4
2.1 Основы теории 4
2.2 Формула Стокса в векторной форме 6
2.3 Исследование 8
3. Список используемой литературы 9
Введение
СТОКС, ДЖОРДЖ ГАБРИЕЛ
(Stokes, George Gabriel) (1819–1903), английский физик и математик. Родился 13 августа 1819 в Скрине (Ирландия). В 1841 окончил Кембриджский университет, с 1849 – профессор математики этого университета. Работы Стокса относятся к области гидродинамики, оптики, спектроскопии, математической физики. В 1845 Стокс разработал теорию вязкости жидкостей, математическую теорию движения вязких жидкостей (уравнение Навье – Стокса). Вывел формулу (1851) для силы сопротивления, действующей на твердый шар малого размера при его движении в бесконечно вязкой среде (закон Стокса). В 1849 опубликовал несколько работ по оптике: исследовал кольца Ньютона, аберрацию, дифракцию, интерференцию и поляризацию света. В 1852 установил, что длина волны люминесценции всегда больше длины волны возбуждающего света (правило Стокса). Показал, что при отражении света происходит сдвиг фазы на половину длины волны.
Стокс внес значительный вклад в математику: исследовал сходимость бесконечных рядов, вывел одну из важнейших формул векторного анализа, ныне носящей его имя.
С 1885 по 1890 был президентом Лондонского королевского общества. Умер Стокс в Кембридже 1 февраля 1903.
2. Основная часть.
2.1
Основы
теории
В установившемся потоке жидкости скорость отдельных частиц (слоёв) различна. В случае течения жидкостей по трубкам наименьшей скоростью обладает слой, перемещающийся около стенки трубки. Скорость остальных, параллельных стенке слоёв возрастает, и максимальная скорость наблюдается по осевой линии трубы.
Определение коэффициента по Стоксу
Теория опыта
Тело, движущиеся в вязкой жидкости, увлекает за собой ближайшие слои жидкости, а те, в свою очередь, - более отдалённые слои. На движение жидкости, на преодоление внутреннего трения тратится энергия. Благодаря этому движущееся тело очень быстро теряет своё ускорение и начинает двигаться равномерно.
Действительно, на движущееся тело действует три силы: сила тяжести Р,
выталкивающая сила f
,
равная Vpg
(V
-объём тела, p
- плотность вязкой жидкости, g
– свободное ускорение) и сила внутреннего трения F
, равная по исследованиям Стокса для шариков малых размеров
F
=6П
r
u
,
,где r
- радиус шарика;
u
- скорость шарика;
n
-коэффициент внутреннего трения.
В начале движения Р >
F
+
f
и шарик движется с ускорением, но так как сила трения возрастает с увеличением скорости, то в некоторый момент сила Р
оказывается равной F
+
f
и шарик начинает с этого момента двигаться равномерно.
Поэтому мы имеем право записать:
Р >
F
+
f
или
mg
=
Vpg
+6П
rnu
;
4/3 П
r
3
б
g
=4/3П
r
3
pg
+6П
rnu
.
Отсюда получаем:
n
=2/9*(б-
p
)/
u
*
r
2
g
,
,где б
– плотность вещества шарика;
p
– плотность жидкости.
По этой формуле и вычисляется коэффициент вязкости.
Формула Стокса в векторной форме
Вихревым вектором
(вихрем), или ротором
векторного поля
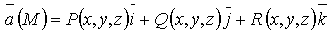 называется вектор, имеющий координаты: называется вектор, имеющий координаты:

Тем самым векторное поле  порождает векторное поле вихря порождает векторное поле вихря 
Через символический вектор Гамильтона 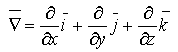 вихревой вектор записывается как векторное произведение вектора вихревой вектор записывается как векторное произведение вектора  на вектор поля на вектор поля  т. е. т. е.

Как легко видеть, выражение

стоящее под знаком поверхностного интеграла в формуле Стокса, представляет собой скалярное произведение 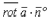 вихря векторного поля вихря векторного поля  на единичный вектор нормали на единичный вектор нормали  к поверхности S
. к поверхности S
.
Следовательно, формулу Стокса
можно представить в векторной форме следующим образом:
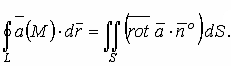
Левая и правая части формулы (3.44) представляют, соответственно, циркуляцию векторного поля  и поток его вихря. Значит, формула Стокса утверждает: циркуляция векторного поля и поток его вихря. Значит, формула Стокса утверждает: циркуляция векторного поля  по замкнутому контуру L
равна потоку его вихря по замкнутому контуру L
равна потоку его вихря  (M)
через поверхность S
, натянутую на этот контур. (M)
через поверхность S
, натянутую на этот контур.
Можно определить проекцию вектора  на любое направление на любое направление  следующим образом: следующим образом:

т.е.  есть вектор, проекция которого на любое направление есть вектор, проекция которого на любое направление  равна пределу отношения циркуляции векторного поля по контуру L
плоской площадки τ, перпендикулярной этому направлению равна пределу отношения циркуляции векторного поля по контуру L
плоской площадки τ, перпендикулярной этому направлению  , к площади этой площадки, когда размеры этой площадки стремятся к нулю. , к площади этой площадки, когда размеры этой площадки стремятся к нулю.
Или другими словами:  есть вектор, нормальный к поверхности, на которой плотность циркуляции достигает наибольшего значения. есть вектор, нормальный к поверхности, на которой плотность циркуляции достигает наибольшего значения.
Это, кроме прочего, означает и то, что вихрь поля (как и градиент, так и дивергенция) не зависит от выбора системы координат, а является характеристикой самого поля.
2.2
Исследование
Для своего опыта я выбрала материал шарика: железо, изучаемая жидкость: машинное масло;
С помощью написанной мною программы, я провела несколько опытов для шариков разного радиуса и для различной скорости падения.
| № опыта
|
Радиус (мм)
|
Скорость (м/с)
|
Вязкость (кг/(м*с))
|
| 1
|
2
|
9,8
|
0,00113
|
| 2
|
4
|
10
|
0,0022148
|
| 3
|
6
|
10,2
|
0,003257059
|
| 4
|
8
|
10,4
|
0,004259231
|
| 5
|
10
|
10,6
|
0,005223585
|
| 6
|
12
|
10,8
|
0,006152222
|
| 7
|
14
|
11
|
0,007047091
|
| 8
|
16
|
11,2
|
0,00791
|
| 9
|
18
|
11,4
|
0,008742632
|
| 10
|
20
|
11,6
|
0,009546552
|
Далее была вычислена средняя вязкость по заданному диапазону скоростей и радиусов:
| Средняя вязкость
|
| 0,005548317
|
Список используемой литературы
1.
Пиявский С.А. «Технология научного исследования», Самара, 2006 г.
2.
Семенов П.А. «Учебник по Delphy 7», Москва, 2007 г.
3.
«Оптика и квантовая физика, лабораторные работы по физике»
|