Разработка модели выбора маршрута железнодорожным транспортом
Авджи Н.И., Мартыненко Т.В.
Общая постановка проблемы
В настоящее время решению задач оптимизации перевозочных процессов и обеспечения безопасности перевозок железнодорожным транспортом посвящено большое количество научных работ. Задача оптимизации перевозочных процессов часто делится на подзадачи: сокращение эксплуатационных затрат, обеспечение роста прибыли, оптимальное размещение маршрутов движения составов, создание условий для развития железнодорожного транспорта. Кроме перечисленных задач, на современном уровне развития железнодорожного транспорта в Украине, очевидна необходимость в развитии системы фирменного обслуживания клиентов.
Анализ литературы
Необходимость такой системы обусловлена спадом объемов перевозок железнодорожным транспортом по причине увеличения доли автомобильного транспорта. Ранее разработанные алгоритмы Юсиповым Р.А. в диссертации «Прогнозирование показателей в оперативных планах поездной и грузовой работы», Шапкиным И.Н. «Организация железнодорожных перевозок на основе информационных технологий», Макаровым В.М. «Разработка и применение математической модели оперативного прогнозирования поездной работы» и другими являются не эффективными, т.к. в них не учитывается качество перевозочного процесса.
Цель статьи
Разработать модель выбора маршрута транспортировки груза железнодорожным транспортом с одной станции на другую. Основным критерием выбора маршрута рассматривать требования к качеству перевозочного процесса и требования клиента.
Разработка модели
Оценка некоторых требований клиентов затруднена отсутствием данных (например, сохранность груза, безопасность перевозки). Многие из требований не могут быть описаны точными значениями по причине невозможности формализованного описания параметров этих факторов либо субъективности отдельных мнений (например, техническое качество состава, состояние станции). Так как требования клиентов к уровню качества обладают значительной неопределенностью, в данной работе предлагается использовать средства муравьиного алгоритма.
В условиях данной задачи в роли муравья выступает поезд, который начиная движение со станции, должен пройти по всем указанным точкам; ребром является железнодорожная сеть между станциями, а вес ребра определяет расстояние между ними. Моделирование поведения муравьёв связано с распределением феромона на тропе – ребре графа. При этом вероятность включения ребра в маршрут отдельного муравья пропорциональна количеству феромона на этом ребре, а количество откладываемого феромона пропорционально длине маршрута. Чем короче маршрут, тем больше феромона будет отложено на его рёбрах, следовательно, большее количество муравьёв будет включать его в синтез собственных маршрутов. Моделирование такого подхода, использующего только положительную обратную связь, приводит к преждевременной сходимости – большинство муравьёв двигается по локально оптимальному маршруту. Избежать этого можно, моделируя отрицательную обратную связь в виде испарения феромона. При этом если феромон испаряется быстро, то это приводит к потере памяти колонии и забыванию хороших решений, с другой стороны, большое время испарения может привести к получению устойчивого локального оптимального решения.
Целевая функция является составной, т.е. состоит из двух частей: общее время пути (1) и качество перевозочного процесса (2). Минимизация количества поездок является более привилегированной, чем минимизация времени.

где Сij – матрица расстояний между точками, Xij – матрица переходов, k – качество перевозочного процесса
Основная идея алгоритма – использование двух типов муравьев: один максимизирует качество перевозочного процесса для выполнения доставки, а второй – время в пути. В рамках данной статьи будет создано начальное решение и описание процесса реинициализации.
На первой стадии клиенты случайным образом связываются поочередно с поездами. На второй стадии создается маршрут для каждого поезда, итеративно добавляя связанных клиентов. Влияние начального решения в алгоритмах муравьиной колонии не так велико, поэтому для инициализации не будет использована трудоемкая процедура.
Мы используем два типа муравьев: качественные и маршрутные. Мощность тропы качественного муравья представляет вероятность для клиента, того, что он будет обслужен неким поездом с определенным качеством. Мощность тропы маршрутного муравья является вероятностью посещения клиента сразу после обслуженного клиента. Пусть L – значение целевой функции, которое является общей длиной маршрута в начальном решении. Изначально будет установлено при i=1..n, j=1..k, i?j. На втором шаге мощность тропы будет переинициализирована.
Создание маршрута муравьем
Для связывания точек с поездами с учетом того, что соблюдается качество перевозочного процесса и грузоподъемность поезда не превышена, будут использоваться такие критерии, как количество клиентов, множество не обслуженных клиентов, множество обслуживаемых клиентов поездом, грузоподъемность поезда, качество перевозочного процесса. Для связывания точек с поездами, нужно пошаговое выполнение действие, а именно:
инициализация множеств и установление грузоподъемности
случайный выбор клиента и назначение его поезду
удаление клиента из множества еще не обслуженных клиентов
выбор поезда для связывания с клиентом, если грузоподъемность более или равна спросу клиента. Выбор поезда производится по правилу
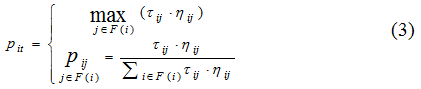
обновление грузоподъемности и добавление клиента в множество клиентов, обслуживаемых поездом
если множество еще не обслуженных клиентов равно 0, то алгоритм заканчивается, иначе – возвращаемся на шаг выбора.
Создание маршрута для каждого поезда
После того, как точки связаны с поездами, происходит решение задачи коммивояжера для каждого поезда. Муравей начинает движение со станции и последовательно строит решение путем выбора следующего клиента из множества доступных клиентов. Действие продолжается пока не будет найден маршрут, а потом повторяется для остальных поездов
Используя предложенную модель, можно определить маршрут перевозки груза железнодорожным транспортом, который будет максимально соответствовать требованиям клиента.
Выводы
Разработана модель выбора маршрута транспортировки груза железнодорожным транспортом. Выбор маршрута строится на базе анализа требований к качеству перевозочного процесса. Рассмотрена задача маршрутизации транспорта с использованием мультиколониальных муравьиных систем (MACS-VRP), которая использует одну муравьиную колонию с двумя типами муравьёв и феромона.
Список литературы
1.Бородин А.Ф., Москалев А.А., Прилепин Е.В. Автоматизированные центры управления местной работой // Железнодорожный транспорт. 2006. №6. – С. 35 – 40.
2. Шапкин И.Н. Организация железнодорожных перевозок на основе дискретных методов управления и твёрдого графика движения поездов // Транспорт. Наука, техника, управление: научный информационный сборник, М.: ВИНИТИ, 2008. – С. 2 – 8.
3. Шапкин И.Н., Щелоков А.И. Грузовым поездам – жесткий график. Железнодорожный транспорт, №9, 2007. – С. 2 – 5.
4. Кузнецов Г.А., Шевелев Ф.А. Реализация, учет и анализ выполнения // Железнодорожный транспорт.2005.№ 8. – С. 22 – 26.
5. http://masters.donntu.edu.ua/2011/fknt/murzin/library/docs/1.htm
6. Пегат А. Нечеткое моделирование и управление / А. Пегат. – М.: БИНОМ. Лаборатория знаний, 2009. – 798 с.
7. Пазойский Ю.О. Математическая модель оптимизации пассажирских перевозок в дальнем сообщении / Ю.О. Пазойский, Д.В. Глазков // Вестник ВНИИЖТ, 2004. № 2. – С. 46 – 47.
|