Приложение Булевой алгебры к синтезу комбинационных схем
Двоичная система логики:
1. Элементы Булевой алгебры:
а) числа
b) переменные
с) операции
d) выражения
e) функции
f) законы
А) Числа:
Два числа: логический ноль и логическая единица в Булевой алгебре отождествляются с понятиями “истина” и ”ложь”.
В) Переменные:
Булевы (логические, двоичные) переменные называются переменными, принимающими значение из множества - ноль и единица.
С) Операции:
1. Отрицание (инверсия).
2. Конъюнкция (логическое умножение).
3. Дизъюнкция (логическое сложение).
Унарной является операция отрицания.
Обозначения:
1. Отрицание  , ù x , ù x
2. Конъюнкция a&b, a·b, ab, aÙb
3. Дизъюнкция aÚb
D) Выражения:
Переменные, знакооперации, соединенные вместе при возможном наличии скобок для задания порядка выполнения операций.
Приоритет задается порядком операции.
Е) Функции:
Булевой (логической) функцией называется такая функция, аргументами которой являются булевы переменные, и сама функция принимает значение из множества ноль и единица.
Областью определения Булевой функции является совокупность 2n
двоичных наборов ее аргументов. Набор аргументов можно рассматривать как n-компонентный двоичный вектор.
Формы задания Булевой функции:
1. Аналитическая (в виде логического выражения)
2. Табличная (в виде таблицы истинности)
3. Графическая
4. Таблично-графическая (в виде карты Карно)
5. Числовая
6. Символическая форма
1) Аналитическая:
_ _
y=(x1
Ú x2
) x3
_ _ _ _ _ _
y=x1
x2
x3
Ú x1
x2
x3
Ú x1
x2
x3
2) Табличная:
x1
|
x2
|
x3
|
_
x1
Ú x2
|
y
|
| 0 |
0 |
0 |
1 |
1 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
0 |
| 1 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
1 |
0 |
Переход от аналитической к табличной однозначен! Обратный переход не является однозначным.
Основные законы (тождества)
1) ab=ba
aÚb=bÚa
2) Ассоциативный:
a(bc)=(ab)c
aÚ(bÚc)= (aÚb) Úc
3) Дистрибутивный:
a(bÚc)=abÚac
aÚ(bc)=(aÚb)(aÚc)
4) Закон двойного отрицания:
=
a=a
5) Тавтологии:
aa=a
aÚa=a
6) Законы нулевого элемента:
a0=0
aÚ0=a
7) Законы единичного элемента:
а1=а
аÚ1=1
8) Законы дополнительного элемента:
_
В Булевой алгебре дополнительным элементом к а является а.
_ _
аÚа=1; аа=0
9) Двойственности (деМоргана):
__ _ _
ab=aÚb
___ _ _
      aÚb=a b aÚb=a b
Cледствия:
ab=aÚb; aÚb=a b
10) Поглощения:
aÚab=a
a(aÚb)=a
11) Сокращения:
_
аÚаb=aÚb
_
a(aÚb)=ab _ _ _ _
Cледствия:
aÚab=aÚb; a(aÚb)=ab
12) Склеивания:
_ _
abÚab=a; (aÚb)(aÚb)=a
Комментарии:
1) Для доказательства законов можно использовать:
а) Метод совершенной индукции.
б) Использование одних законов для доказательства других законов.
Метод совершенной индукции состоит в доказательстве эквивалентности левой и правой части на всем множестве наборов аргументов. Для этого составляется таблица истинности.
2) Большинство законов задается парой соотношений, при этом одно соотношение можно получить из другого заменив операции конъюнкции на дизъюнкцию или дизъюнкцию на конъюнкцию (метод не применим в законах, в которых участвуют константы). С константами же константы заменяются на противоположные значения. (Дуальность законов Булевой алгебры)
3) Некоторые законы можно распространять на произвольное число элементов.
4) В любом законе можно заменить любую букву на произвольное логическое выражение.
5) Законы применяются для упрощения Булевых функций.
Разнообразие Булевых функций.
1. Булева функция от одной переменной.
2. Возможные функции от двух переменных.
Определение: Булева функция от n аргументов fn
(x) называется вырожденной по аргументу xi
, если ее значение не зависит от этого аргумента, то есть для всех наборов аргументов имеет место равенство:
f(x1
, x2
, ... , xi-1
, 0, xi+1
, ... , xn
) = f(x1
, x2
, xi-1
, 1, xi+1
, ... , xn
).
Функция запрета x1
Dx2
принимает значение, равное нулю при равенстве запрещающей переменной (x2
) единице и повторяет значение аргумента x1
при равенстве запрещающей переменной нулю.
Понятие импликации в Булевой алгебре отождествляется с выражением следования (если ... то ... ).
Пример: Имеют место два простых высказывания.
А. На небе тучи.
В. Идет дождь. В®А
| А |
В |
В®А |
| f |
f |
t |
| f |
t |
f |
| t |
f |
t |
| t |
t |
t |
Из истины не может следовать ложь!
Некоторые функции от трех переменных.
| Значение аргументов |
Значение функций
|
| Сумма по модулю 2 |
Исключающее ИЛИ |
Функция мажоритарности |
| x1
|
x2
|
x3
|
x1
Åx2
Åx3
|
XOR (x1
,x2
,x3
) |
x1
#x2
#x3
|
| 0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
0 |
1 |
| 1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
Функция - сумма по модулю 2 и исключающее ИЛИ являются эквивалентными только для двух аргументов.
n
Общее разнообразие функций от n аргументов равно 22
В самом компактном виде любую Булеву функцию можно представить символически:  , где n-количество аргументов, а N-десятичный эквивалент двоичного набора значений функции на упорядоченном множестве аргументов. , где n-количество аргументов, а N-десятичный эквивалент двоичного набора значений функции на упорядоченном множестве аргументов.
Пример:
f3
(x)=x1
Åx2
Åx3
=
Невырожденные функции от двух переменных с добавлением функции отрицания принято называть функциями Булевой алгебры. С учетом обращаемости некоторых базовых функций к некоторым аргументам, их общее количество равно девяти.
Нормальные формы Булевых функций
Нормальные формы - это особый класс аналитических выражений, используемых при решении задачи минимизации Булевых функций и для перехода от табличной формы задания к аналитической. Нормальные формы строятся на основании операций конъюнкции, дизъюнкции и отрицания, причем отрицание только единственной переменной.
Определение: Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция (дизъюнкция) конечного числа попарно различимых переменных или их отрицаний.
Элементарную конъюнкцию (дизъюнкцию) принято называть конъюнктивным (дизъюнктивным) термом.
В частном случае терм, как конъюнктивный так и дизъюнктивный может состоять из единственной буквы (литерала). Под буквой будем понимать аргумент Булевой функции и его отрицания.
Примеры конъюнктивных термов:
_ _
x1
, x2
, x1
x3
, x2
x4
x5
(терм)
___ _
x1
x2
, x1
x2
x3
(не терм)
Рангом терма называется количество букв входящих в него.
Дизъюнктивной (конъюнктивной) нормальной формой Булевой функции называется дизъюнкция (конъюнкция) конечного числа попарно различимых конъюнктивных (дизъюнктивных) термов.
Каноническая нормальная форма.
Конституентой единицы (нуля) называется конъюнктивный (дизъюнктивный) терм максимального ранга. Т.е. для Булевой функции от n переменных конституента включает в себя n букв.
Свойство конституенты: Конституента единицы (нуля) принимает значение единицы (нуля) на одном и только одном наборе аргументов.
Пример: _ _
n=4 x1
x2
x3
x4
(1010)=1
_ _ _
x1
Úx2
Úx3
Úx4
=0
Определение: Дизъюнктивная (конъюнктивная) нормальная форма называется канонической, если все ее дизъюнктивные (конъюнктивные) термы представляют собой конституенты единицы (нуля). Иногда канонические формы называют совершенными.
Пример получения канонических форм:
y=x1
Åx2
| x1
|
x2
|
y |
Конституента единицы |
Конституенты нуля |
| 0 |
0 |
0 |
- |
x1
Úx2
|
| 0 |
1 |
1 |
 1
x2 1
x2
|
- |
| 1 |
0 |
1 |
x1
 2 2
|
- |
| 1 |
1 |
0 |
- |
 1
Ú 1
Ú 2 2
|
КДНФ - каноническая дизъюнктивная нормальная форма:
_ _
y=x1
x2
Úx1
x2
ККНФ - каноническая конъюнктивная нормальная форма:
_ _
y=(x1
Úx2
)(x1
Úx2
)
1) С помощью канонических форм наиболее просто осуществляется переход от табличной формы задания Булевой функции к аналитической.
2) С помощью канонических форм можно осуществить преобразование любой функции в Булев базис.
3) Любая Булева функция за исключением логического нуля и логической единицы имеет единственные КДНФ и ККНФ. Логическую единицу можно представить в виде КДНФ и логический ноль в виде ККНФ.
4) Правило перехода от табличной формы задания Булевой функции к аналитической:
а) в таблице истинности выделяются все наборы аргументов, при которых функция равна единице (нулю).
б) для каждого из этих наборов составляют конституенты единицы (нуля).
в) объединением конституенты единицы (нуля) знаками дизъюнкции (конъюнкции) получается аналитическая форма в виде КДНФ (ККНФ).
Пояснение: при составлении конституент единицы (нуля) используют следующее правило:
Если некоторый аргумент принимает на наборе значение равное нулю, то в конституенту единицы он входит с отрицанием, а в конституенту нуля без него.
5) КДНФ и ККНФ представляют собой две различные, но эквивалентные аналитические формы булевой функции. Это означает, что из одной формы можно получить другую, используя законы Булевой алгебры.
_ _ _ _ _ _ _ _ _ _
y=(x1
Úx2
)(x1
Úx2
)=x1
x1
Úx1
x2
Úx2
x1
Úx2
x2
=x1
x2
Úx2
x1
=x1
x2
Úx1
x2
(КДНФ)
6) Принципиально существует другой способ получения ККНФ:
а) составляется КДНФ, но не для самой, а для ее отрицания.
б) берется отрицание над полученной КДНФ, которое снимается с применением закона двойственности.
_ _ _ = ------------ ----- ---- _ _
    y=x1
x2
Úx1
x2
, y=y=x1
x2
Úx1
x2
=x1
x2
x1
x2
=( x1
Úx2
)(x1
Úx2
) y=x1
x2
Úx1
x2
, y=y=x1
x2
Úx1
x2
=x1
x2
x1
x2
=( x1
Úx2
)(x1
Úx2
)
Разнообразие двоичных алгебр
В связи с тем, что любую сколь угодно сложную Булеву функцию можно представить в канонических формах, то есть записать ее с помощью операций отрицания, конъюнкции и дизъюнкции эта система Булевых операций обладает свойством функциональной полноты, т.е. образует так называемый базис. Естественно предположить, что система Булевых операций является не единственной, с помощью которой можно образовать некоторый базис.
В принципе любую из базовых функций можно отождествить соответствующей операцией и на основе совокупности этих операций построить двоичные алгебры, отличные от Булевой. К наиболее распространенным двоичным алгебрам относятся: алгебра Жигалкина (Å, &); алгебра Вебба (Пирса) (¯); алгебра Шеффера ( | ). В каждой из этих алгебр действуют собственные законы. Естественно существуют взаимно однозначные переходы от операций одного базиса к операциям другого.
Числовое представление Булевых функций
Для любой Булевой функции можно предложить две числовые формы, основанные на перечислении десятичных эквивалентов наборов аргументов на которых функция принимает значение единицы (нуля).
f3
(x)= (0,2,6,7) - от этой числовой формы легко перейти к КДНФ путем замены каждого из наборов в перечислении конституенты единицы. (0,2,6,7) - от этой числовой формы легко перейти к КДНФ путем замены каждого из наборов в перечислении конституенты единицы.
_ _ _ _ _ _ _ _ _ _ _
y=x1
x2
x3
Úx1
x2
x3
Úx1
x2
x3
Úx1
x2
x3
=x1
x3
(x2
Úx2
)Úx1
x2
(x3
Úx3
)=x1
x3
Úx1
x2
(ДНФ)
f3
(x)= &(1,3,4,5) &(1,3,4,5)
_ _ _ _ _ _
y=(x1
Úx2
Úx3
) (x1
Úx2
Úx3
) (x1
Úx2
Úx3
) (x1
Úx2
Úx3
) (*)
Преобразование произвольной аналитической формы Булевой функции в нормальную
В Булевой алгебре в виде теоремы доказывается следующее утверждение: существует единый конструктивный подход, позволяющий преобразовать аналитическое выражение Булевой алгебры в произвольной форме к нормальной форме.
Пример:
 _ _ _ _ _ _ _ _ _ _ _ _
y=f4
(x)=(x1
x2
Úx2
x3
)(x1
|x4
)=(x1
x2
Úx2
x3
)(x1
x4
)=(x1
x2
Úx2
x3
)(x1
Úx4
)=
_ _ _ _ _ _ _ _ _ _
=x1
x2
Úx1
x2
x4
Úx1
x2
x3
Úx2
x3
x4=
x1
x2
Úx1
x2
x3
Úx2
x3
x4
=x1
(x2
Úx2
x3
)Úx2
x3
x4
=
_ _ _ _
=x1
(x2
Úx3
) Úx2
x3
x4
=x1
x2
Úx1
x3
Úx2
x3
x4
(КДНФ)
Замечания:
1) В общем случае любая Булева функция может иметь несколько КДНФ, отличающихся либо количеством термов, либо количеством букв в этих термах.
2) При построении комбинационной схемы, реализующей данную функцию по ее нормальной форме предпочтительней та, которая обладает наименьшим числом термов и наименьшим количеством букв в этих термах.
3) По сравнению со схемой, построенной по ДНФ, схема, построенная по скобочной форме (*), является более предпочтительной т.к. при одном и том же числе логических элементов (И, ИЛИ) содержат меньшее число входов (9 вместо 10).
Задача преобразования нормальной формы Булевой функции в скобочной форме называют задачей фактеризации.
4) Сущность конструктивного подхода при получении ДНФ состоит в следуюшем:
а) преобразование операций не-Булевого базиса к операциям Булевого базиса (см. последние строки таблицы)
б) снятие отрицаний над выражениями с применением законов двойственности
в) раскрытие скобок с применением дистрибутивного закона
г) упрощения выражения с применением закона поглощения
Приведение произвольных нормальных форм Булевой функции к каноническим
Для приведения произвольной ДНФ к КНФ необходимо использовать правило дизъюнктивного развертывания применительно к каждому из неполных конъюнктивных термов.
_ _
P=P(xi
Úxi
)=Pxi
ÚPxi,
где P-неполный конъюнктивный терм (ранг этого терма
меньше n), а xi
- недостающий в терме аргумент.
Пример:
_ _ _ _ _ _ _ _ _ _
y=x1
Úx2
x3
(ДНФ)=x1
(x2
Úx2
)(x3
Úx3
) Úx2
x3
(x1
Úx1
)=x1
x2
x3
Ú x1
x2
x3
Ú
 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Úx1
x2
x3
Úx1
x2
x3
Ú x1
x2
x3
Ú x1
x2
x3
(КДНФ)
Замечание:
После раскрытия скобок могут получиться одинаковые термы, из которых нужно оставить только один.
y= (0,1,2,3,5)=f3 (0,1,2,3,5)=f3
Преобразование КНФ к ККНФ реализуется путем применения правила конъюнктивного развертывания к каждому неполному дизъюнктивному терму.
_ _
P=PÚxi
xi
=(PÚxi
)(PÚxi
)
_ _ _ _ _ _ _ _ _ _
y=x1
Úx2
x3
(ДНФ)=(x1
Úx2
)(x1
Úx3
)(КНФ)=(x1
Úx2
Úx3
x3
)(x1
Úx3
Úx2
x2
)=
 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
=(x1
Úx2
Úx3
)(x1
Úx2
Úx3
)(x1
Úx2
Úx3
)(x1
Úx2
Úx3
)(ККНФ)
y= (4,6,7) (4,6,7)
Минимизация булевых функций на картах Карно(см
.
Практику)
.
Метод Квайна-МакКласски базируется на кубическом представлении булевых функций.
Кубическое представление булевых функций
.
В кубическом представлении булевой функции от n переменных все множество из 2n
наборов ее аргументов рассматривается как множество координат вершин n-мерного куба с длинной ребра равной 1. В соответствии с этим наборы аргументов, на которых булева функция принимает значение равное 1 принято называть существенными вершинами.
Существенные вершины образуют так называемые ноль-кубы (0-кубы). Между 0-кубами существует отношение соседства и определена операция склеивания. Два 0-куба называются соседними если они отличаются только по одной координате.
Пример :n=4 0101
0001 - два соседних 0-куба
результат склеивания : 0x01 (*)
Склеивание 2-х соседних 0-кубов дает в результате 1-куб. Координата, отмечаемая символом х, называется свободной (независимой, несвязанной), а остальные (числовые) координаты называются зависимыми (связанными). Аналогичное отношение соседства существует между 1-кубами, в результате склеивания которых получается 2-куб.
0х01
0х11 - 0хх1 (**)
В продолжении аналогии два r-куба называются соседними если они отличаются только по одной (естественно зависимой) координате.r-куб содержит r независимых и n-r зависимых координат. В результате склеивания 2-х соседних r-кубов образуется (r+1)-куб содержащий r+1 независимую координату.
Операция склеивания над кубами соответствует применению закона склеивания к конъюнктивным термам, отождествляемым с этими кубами.
_ _ _ _ _ _ _
х1
х2
х3
х4
Ú х1
х2
х3
х4
= х1
х3
х4
(0101) (0001) (0х01)
_ _ _ _
для (**) х1
х3
х4
Ú х1
х3
х4
= х1
х4
(0х01) (0х11) (0хх1)
Определения
.
Кубическим комплексом K0
(f) булевой функции f называется множество 0-кубов этой функции. В общем случае кубическим комплексом Kr
(f) булевой функции f называется объеденение множеств кубов всех размерностей этой функции
m
k(f)=UKr
(f) m-максимальная размерность кубов функции f.
r=0
Пример получения кубических комплексов
f3
(x)=V(1,2,3,6,7) |001 (1) |0x1 (1-3) (1)
(f=1) |010 (2) |01x (2-3) (2)
K0
(f)=|011 (3) K1
(f)=|x10 (2-4) (3) K2
(f)=|x1x (2-5)
|110 (4) |x11 (3-5) (4)
|111 (5) |11x (4-5) (5)
K3
(f)=пустому множеству
K(f)=K0
(f)UK1
(f)UK2
(f)
Для получения кубического комплекса K(f) необходимо провести всевозможные операции склеивания над 0-кубами, 1-кубами и т.д. до тех пор пока на очередном шаге не получится Kr+1
(f)=пустому множеству. При склеивании 1-кубов 2-кубы представлены в 2-х экземплярах как результаты склеивания 2-х различных пар 1-кубов.
Распространяя этот принцип можно утверждать, что r-кубы как результат склеивания (r-1)-кубов получаются в r-кратном количестве экземпляров.
Куб, входящий в состав кубического комплекса K(f) называется максимальным, если он не вступает ни в одну операцию склеивания.
В приведенном примере максимальными кубами являются х1х и 0х17.
Геометрическая интерпретация кубов
малой размерности
.
Графическое представление булевых функций
.
Подобный подход носит ограниченный характер и как правило является наглядным для булевых функций от 2-х и 3-х переменных.
F3
(x)=V(1,2,3,6,7)
(f=1)
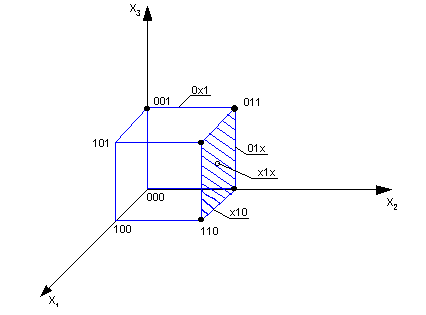
Геометрическим местом 0-куба является точка, представляющая существенную вершину.
Два соседних 0-куба являются концами какого-либо ребра.
Геометрическим местом 1-куба является ребро, замыкаемое склеивающимися 0-кубами, образующими данный 1-куб.
Два параллельных ребра, образующих грань, являются образами склеивающихся 1-кубов. В соответствии с этим геометрической интерпретацией 2-куба является грань, образуемая парой параллельных ребер. Так как любую грань можно определить одной из пар параллельных ребер, 2-куб может быть получен как результат склеивания двух различных пар 1-кубов, то есть представляется в двух экземплярах.
Геометрическим образом 3-куба можно считать 3-х мерный куб. Так как он может быть образован 3-мя способами как пара параллельных граней, то при склеивании он получается в трех экземплярах.
Покрытия булевых функций
.
Между кубами различной размерности, входящих в кубический комплекс K(f), существует отношение включения или покрытия. Принято говорить, что куб А меньшей размерности покрывается кубом Б большей размерности, если куб А включается в куб Б. Это означает, что при образовании куба Б хотя бы в одном склеивании учавствует куб А.
Отношение включения (покрытия) между кубами принято обозначать АÌБ. В теории множеств отношение включения связывает между собой некоторое множество и его подмножества.
Для рассмотренного примера отношения включения имеют место между 001Ì0х1; 011Ìx11Ìx1x... любой 1-куб покрывает 2 0-куба, 2-куб - 4 0-куба и 2 1-куба, 3-куб покрывает 8 0-кубов, 12 1-кубов и 6 2-кубов.
Покрытием булевой функции f называется такое подмножество кубов из кубического комплекса K(f), которое покрывает все существенные вершины функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие конъюнктивный терм, для любого покрытия можно представить некоторую ДНФ булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K0
(f), покрытие c0
(f)=K0
(f). Этому покрытию соответствует КДНФ.
Для примера покрытием является также
|0x1
|01x
c1(f)=K1(f)=|x10
|x11
|11x
этому покрытию соответствует ДНФ вида
_ _ _ _ _ _ _ _ _ _
f=x1
x3
vx1
x2
vx2
x3
vx2
x3
vx1
x2
приведенная ДНФ не является минимальной.
В качестве минимальной еще одного покрытия можно использовать множество максимальных кубов
|0x1
c2
(f)=|x1x
Действительно, куб 0х1 покрывает существенные вершины 0х1É(001, 011), а куб x1xÉ(010, 011, 110, 111).
Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытие c2
(f) соответствует ДНФ вида х1
х3
vx2
. Эта ДНФ является минимальной. Покрытие булевой функции, которое соответствует минимальной ДНФ называется минимальным покрытием.
Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае все множество максимальных кубов является минимальным покрытием. Это справедливо для нашего примера. В общем случае множество максимальных кубов является избыточным и для получения минимального покрытия достаточно взять некоторое его подмножество.
Пример : f3(x)=V(0,1,4,6,7)
(f=1)
|000 (1) |00x (1-2)
|001 (2) |x00 (1-3)
K0
(f)=|100 (3) K1
(f)=|1x0 (3-4)
|110 (4) |11x (4-5)
|111 (5)
Для данного примера множество максимальных кубов совпадает с комплексом K1
(f). Z(f)=K1
(f)
Минимальными покрытиями являются
|00x |00x
с1
(f)=|11x c2
(f)=|11x
|x00 |1x0
Из анализа покрытия существенных вершин максимальными кубами из комплекса K1
(f) следует :
1) Куб 00х должен обязательно включаться в покрытие, так как только он покрывает существенную вершину 001, аналогично 11х покрывает 111.
Множество максимальных кубов без которых не может быть образовано покрытие булевой функции называется ядром покрытия T(f)=|00x
|11x
2) Так как ядром покрытия кроме существенных вершин 001 и 111 покрываются также существенные вершины 000 и 110, то не покрытой ядром остается только существенная вершина 100. Для ее покрытия достаточно взять 1 из оставшихся максимальных кубов (х00 или 1х0).
Выводы :
Задача получения минимальной ДНФ сводится к задаче получения минимального покрытия.
Получение минимального покрытия реализуется в таком порядке : а) Находится множество максимальных кубов б) Выделяется ядро покрытия в) Из максимальных кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое покрывает существенные вершины, не покрытые ядром.
Цена покрытия
.
Цена r-куба представляет собой количество несвязанных координат. Sr=n*r
Для оценки качества покрытия используют два вида цены покрытия :
m
1) Sa
=åSr
Nr
, где Nr
- количество r-кубов, входящих в по-
r=0
крытие,m- максимальная размерность куба. Цена Sa
представляет собой сумму цен кубов, входящих в покрытие.
2) Sb
=Sa
+k, где k - количество кубов, входящих в покрытие
m m
Sa
=å(n-r) Nr
; Sb
=å(n-r)(Nr
+1)
r=0 r=0
Под минимальным покрытием понимают покрытие, обладающее минимальной ценой Sa
по сравнению с любым другим покрытием этой функции.
Можно показать, что покрытие, обладающее минимальной ценой Sa
обладает также и минимальной ценой Sb
.
Пример : f3
(x)=V(0,1,4,6,7)
(f=1)
C0
(f)=K0
(f) ; Sa
=5*3=15 ; Sb
=Sa
+5=20
C1
(f)=K1
(f) ; Sa
=4*2=8 ; Sb
=Sa
+4=12
Cmin
(f) : Sa
=3*2=6 ; Sb
=9
Цена покрытия Sa
представляет собой количество букв, входящих в ДНФ, которая соответствует данному покрытию.
Цена Sb
представляет для ДНФ сумму количества букв и количества термов.

Цена покрытия хорошо согласуется с ценой схемы по Квайну, которая строится по нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ
=9=Sb
(9-число входов).
В принципе, между SQ
и ценами Sa
и Sb
существует соотношение Sa
£ SQ
£ Sb
Это неравенство имеет место при следующих допущениях по комбинационной схеме :
1) Схема строится по нормальной форме (ДНФ или КНФ).
2) Схема строится на элементах булевого базиса (И, ИЛИ).
3) На входы схемы можно подавать как прямые, так и инверсные значения входных переменных, представляющие собой значения аргументов булевой функции (схема с парафазными входами). Элементы НЕ (инвертора в схеме отсутствуют.
Нулевое покрытие булевой функции и получение минимальной КНФ
.
Выше было рассмотрено покрытие булевой функции на наборах аргументов для которых функция равна единице.
Такие покрытия можно назвать единичными. Наряду с единичными покрытиями существуют и нулевые, для которых покрываются наборы аргументов, на которых функция равна нулю, то есть покрытие реализуется для существенных вершин, но не самой функции, а ее отрицания (инверсии).
Нулевое покрытие строится также как и единичное, но только для отрицания исходной функции.
f3
(x)=V(0,1,4,6,7) f3
(x)=&(2,3,5)
(f=1) (f=0) _ |010
K0
( f )=|011
_ _ |101
C0( f )= K0
( f ) Sa
=9 Sb
=12
_ _ _
K1( f )=|01x Z( f )=Cmin
( f )=|01x Sa
=5 Sb
=7
|101
Цена минимального нулевого покрытия оказалась меньше цены минимального единичного покрытия.
Так как заранее предсказать невозможно, какое из минимальных покрытий данной функции, единичное или нулевое, будет иметь меньшую цену, то для построения схемы, обладающей минимальной ценой по Квайну, целесообразно решать задачу минимзации в отношении обоих покрытий.
Импликанты булевой функции
.
Системы импликант
.
Решение задачи минимизации булевой функции методом Квайна и усовершенствованным методом Квайна-МакКласски базируется на понятиях импликант и их систем.
Определение : Булева функция g(x) называется импликантой булевой функции f(x), если для любого набора аргументов, на которых g(x)=1, f(x) также равна единице.
~ ~~
g( x )=1 => f( x )=1, где х - некоторый набор аргументов.
Свойства импликант :
1) Между импликантой и самой функцией существует отношение включения g(x)Ìf(x).
2) Можно утверждать, что для любого набора аргументов, на котором функция равна нулю, ее импликанта также равна нулю.
3) Если g(x) и j(x) являются импликантами функции f(x), то их дизъюнкция также является импликантой этой функции.
Простейшими примерами импликант могут служить конъюнктивные термы, входящие в ДНФ данной функции.
Пример : для f3
(x)=V(0,1,4,6,7) (#)
(f=1) _ _ _
импликантами являются х1
х2
х3
; х1
х2
х3
; х1
х2
;...
Произвольная дизъюнкция этих термов также является импликантой функции.
Определение : Простой (первичной) импликантой булевой функции называется конъюнктивный терм, который сам является импликантой этой функции, но никакая его собственная часть уже не является импликантой этой функции.
Под собственной частью терма понимается новый терм, полученный из исходного, путем вычеркивания произвольного числа букв.
Для данного примера функции (#) простыми импликантами являются : _ _ _
х1
х2
х3
; х1
х2
х3
; х1
х2
;...
Множеству простых импликант можно поставить в соответствие множество максимальных кубов.
Определение : Дизъюнкция всех простых импликант булевой функции представляет собой ДНФ этой функции, которая называется сокращенной - СДНФ.
Для функции (#) из приведенного примера
_ _ _ _ _
СДНФ : y= х1
х2
v х1
х2
vх2
х3
v х1
х3
Понятие «сокращенное» присвоено ДНФ в том смысле, что она, как правило, содержит меньшее количество букв и термов по сравнению с КДНФ. Для нашего примера КДНФ содержит 15 букв и 5 термов, а СДНФ - 8 букв и 4 терма.
Аналогия
между импликантами и кубическим представлением Булевой функции
Любому кубу из К(f) можно поставить в соответствие конъюнктивный терм который можно рассматривать как импликанту булевой функции .Любой простой импликанте булевой функции соответствует максимальный куб ,и в свою очередь множество всех простых импликант соответствует множеству Z(f) всех максимальных кубов К(f).
Таким образом можно провести некоторую аналогию между сокращенной СДНФ и Z(f).
В отношении импликант булевой функции также как и в отношении кубов соответствующих им существует отношение покрытия.
Принято считать ,что импликанта покрывает некоторую существенную вершину или в общем случае некоторый куб из К(f) ,если значение импликанты на наборе аргументов представляющем данную существенную вершину равно 1 или в общем случае значение импликанты равно 1 для всех существенных вершин покрываемых кубом из К(f).
ПРИМЕР : импликанта х1
х2
покрывает существенные вершины(110,111) и в свою очередь покрывает куб 11х.
Определение :множество импликант булевой функции образует полную систему импликант ,если любая существенная вершина булевой функции покрывается хотя бы одной импликантой этого множества.
Если считать ,что в полную систему импликант включаются импликанты только в виде конъюнктивныхтермов и не включает импликанты в виде дизъюнктивных термов ,то полной системе импликант можно поставить в соответствие некоторое множество кубов из К(f) образующих покрытие булевой функции f .
Так например ,кубам из кубического комплекса К°(f) соответствует полная система импликант ,представляющая собой множество конституент 1 данной функции f. В свою очередь множеству максимальных кубов Z(f),естественно образующих покрытие булевой функции ,соответствует полная система простых импликант.
Определение :система простых импликант называется приведенной ,если она является полной ,а никакая ее собственная часть уже не образует полную систему импликант.
Для функции y= x 1
x 2
Ú 1 1
 2
Ú 2
Ú 2 2
 3
Ú x 1 3
Ú x 1
 3
(*) 3
(*)
система простых импликант
{ x 1
x 2
, 1 1
 2
, 2
, 2 2
 3
, x 1 3
, x 1
 3
} 3
}
является полной ,но не является приведенной ,т.к. из нее можно исключить одну из импликант не нарушая полноты системы .{ 2 2
 3
или x1 3
или x1
 2
} 2
}
Определение: Дизъюнкция всех простых импликант ,образующих некоторую приведенную систему называется тупиковой ДНФ булевой функции или ТДНФ
Для функции (*)существуют две ТДНФ

1) у= x 1
x 2
Ú 1 1
 2
Ú 2
Ú 2 2
 3 3
2) у= x 1
x 2
Ú 1 1
 2
Ú x 1 2
Ú x 1
 3 3
В данном случае они совпадaют с минимальной ДНФ. Но в общем случае это утверждение не справедливо. Т.е. минимальная ДНФ обязательно является ТДНФ но не любая ТДНФ является МДНФ. Таким образом множество МДНФ является подмножеством ТДНФ.
Определение: простая импликанта булевой функции называется существенной если она и только она покрывает некоторую существенную вершину этой функции.
Множество существенных импликант соответствует максимальным кубам образующим ядро покрытия.
ПОСЛЕДОВАТЕЛЬНОСТЬ действий для решения канонической задачи минимизации методом Квайна-Мак-Класки.
1)Нахождение множества максимальных кубов или простых импликант функции.
2)Выделение ядра покрытия.
3)Дополнение множества кубов ,принадлежащих ядру покрытия таким минимальным подмножеством из максимальных кубов ,не входящих в ядро покрытия ,для получения покрытия с минимальной ценой.
С точки зрения последовательного преобразования ДНФ булевой функции с целью их упрощения каноническая задача минимизации может быть представлена в виде КДНФ.
КДНФÞСДНФÞ{ТДНФ}Þ{МДНФ}
Распространение терминологии в отношении нулевого покрытия определяется на понятии импликанта как соответствие импликанте и на системе импликант.
ПРИМЕР: (минимизация булевой функции методом Квайна-Мак-Класки)
1) f4
(x)=V(0,1,5,7,8,10,12,14,15)
(f=1)
f4
(x)=&(2,3,4,6,9,11,13)
(f=0)
На этапе получения множества максимальных кубов целесообразно разделить множество ноль - кубов (К°(f)) на ряд подмножеств ,отличающихся количеством единиц .
В операцию склеивания в этом случае могут вступать только кубы ,относящиеся к соседним подмножествам ,то есть отличающиеся на единицу
ì000X ü
ï X000 ÷ K°(f)=C°(f)
ï 0X01 ÷
Z(f)= í 01X1 ý Sa
=36
ê X111 ú Sb
=45
ê 111Xú
î 1XX0 þ
K1
(f)=C1
(f) Sa
=10*3=30
Sb
=40
Z(f)=C3
(f) Sa
=20
Sb
=27
При минимизации не полностью определенной булевой функции множество максимальных кубов определяется на объединении множества существенных вершин и безразличных наборов в целях получения кубов наибольшей размерности .
2) Определение ядра покрытия .
Выполнение этого этапа реализуется с помощью таблицы покрытий .
Kаждая строка таблицы - максимальный куб(простая импликанта).
Каждый столбец - существенная вершина булевой функции (безразличные наборы не включаются).
Элементы этой таблицы отражают отношение покрытия ,то есть на пересечении i-ой строки и j-ого столбца ставится некоторая отметка в том случае если i-ый максимальный куб покрывает j-ую вершину .
Таблицу покрытий иногда называют импликантной таблицей с учетом того ,что каждый максимальный куб соответствует простой импликанте а существенные вершины конституантам
единицы(нуля).
Существенные вершины
макс.
Кубы
|
0000 |
0001 |
0101 |
0111 |
1000 |
1010 |
1100 |
1110 |
1111 |
| A |
000X |
* |
* |
| |
| |
| |
| |
| B |
X000 |
* |
| * |
| |
| |
| |
| C |
0X01 |
* |
* |
| |
| |
| |
| |
| D |
01X1 |
* |
* |
| |
| |
| |
| |
| E |
X111 |
* |
| |
| |
| |
| |
* |
| F |
111X |
| |
| |
| |
| |
* |
| 1XX0 |
| * |
| * |
| * |
| * |
| a |
b |
c |
d |
| |
| |
| |
| |
e |
Для полностью определенной булевой функции количество меток в каждой строке равно числу ноль - кубов покрываемых кубом данной строки .Для не полностью определенной функции количество меток в строке зависит от количества безразличных наборов покрываемых данным кубом .Для нахождения кубов ,принадлежащих ядру покрытия в таблице ищутся столбцы с единственной меткой .Строка ,которой принадлежит эта метка определяет куб ядра .
Т(f)={1XX0}
3) Определение множества минимальных покрытий .
На этом этапе из множества максимальных кубов не принадлежащих ядру покрытия ,выделяются такие минимальные подмножества ,с помощью каждого из которых покрываются оставшиеся вершины (не покрытые ядром) .
Реализацию этого этапа целесообразно производить с использованием упрощенной таблицы.
В упрощенной таблице вычеркнуты все кубы принадлежащие ядру и вершины покрываемые ядром.
Для решения задачи 3-го этапа можно использовать один из 3-х методов или их комбинацию:
1) Метод простого перебора
2) Метод Петрика
3) Дальнейшее упрощение.
1)На данном этапе целесообразно ввести обозначение максимальных кубов и существенных вершин.
Максимальные кубы обозначены в таблице А...F
1-ый методцелесообразно применять для упрощенной таблицы небольшого объема .Этот метод не дает гарантии получения всех максимальных покрытий.
Для нашего примера все кубы входящие в упрощенную таблицу покрытий обладают одной размерностью(то есть необходимо выбрать минимальное количество этих кубов для покрытия всех оставшихся существенных вершин).
Из таблицы видно ,что минимальное число кубов равно трем.К возможным вариантам покрытий относятся:
ì Tüì Tü
C min
1
(f)= êAú Cmin
1
(f)= êBú,...
ïCúêCú
îE þîE þ
2)Достоинство этого метода-получение всех минимальных покрытий.
Метод базируется на составлении логического выражения , представляющего собой условие покрытия всех вершин из упрощенной таблицы покрытий и преобразования этого выражения .
Y=(AvB)(AvC)(CvD)(DvE)(EvF)=(AvBC)(DvCE)(EvF)=
=(AvBC)(DEvCEvDFvCEF)=
=(ADEvACEvADFvBCDEvBCEvBCDF)
Каждый из пяти конъюнктивных термов соответствует покрытию булевой функции(с учетом дополнения ядром),каждому из которых можно поставить в соответствие тупиковую ДНФ.
Последний терм не соответствует минимальному покрытию ,то есть данная функция имеет четыре минимальных покрытия.
3) Дальнейшее упрощение состоит в применение двух операций : а)Вычеркивание лишних строк.
б)Вычеркивание лишних столбцов.
Если множество меток i-й строки является подмножеством меток j-й строки и куб i имеет небольшую размерность, чем куб j, то из таблицы можно вычеркнуть i-ю строку так как существенные вершины покрываемые i-м кубом будут с гарантией покрыты j-м кубом.
В дальнейшем рекомендуется построить новую упрошенную таблицу.
В отношении новой таблицы можно использовать один из трех методов: 1) Метод простого перебора.
2)Метод Петрика.
3)Дальнейшее упрощение.
Функциональная полнота системы булевых функций
.
Система булевых функций S={y1
,y2
,...,ym
}называется функционально полной ,если с помощью функций этой системы можно выразить любую сколь угодно сложную булеву функцию с использованием метода суперпозиции, возможно многократно.
Под суперпозицией в отношении булевых функций понимается подстановка одних функций в другие вместо их аргумента.
Примерами полных систем являются :
1)S1
={ù,&,Ú}(булев базис)
Обоснованность утверждения о функциональной полноте этой системы базируется на возможности представления любой булевой функции в нормальной форме ,которая является комбинацией операций отрицания ,конъюнкции и дизъюнкции, применительно к аргументу этой функции.
Система S1
={ù,&,Ú}является избыточной так как из нее можно удалить одну из функций (& или Ú) без нарушения функциональной полноты.
Получаемые при этом системы S2
={ù,&}иS3
{ù,&,Ú}обычно называют сокращенным булевым базисом .
Недостающие операции(Úв системе S2
и & в системе S3
) могут быть выражены с помощью следствий из законов
____
Де Моргана : x1
V x2
=  1 1
 2 2
_____
x1
x2
=  1
v 1
v 2 2
Функциональная полнота системы булевых функций называется минимальной ,если удаление из нее какой-либо функции приводит к нарушению свойства функциональной полноты.
Системы из одной функции S4
=¯(стрелка Пирса)
S5
=|(штрих Шеффера)
которые принято называть универсальным базисом.
2)Базис Жегалкина S6
= {&, Å, 1}
Понятие функциональной полноты системы булевых функций связано с аналогичным понятием для системы логических элементов.
Эта связь заключается в следующем :
Если каждой функции из некоторой функционально полной системы сопоставить логический элемент, реализующий эту функцию ,то система логических элементов соответствующая некоторой функционально полной системе булевых функций естественным образом оказывается тоже функционально полной .
Задача синтеза комбинационных схем с использованием функционально полной системы логических элементов можно построить комбинационную схему реализующую любую наперед заданную ,сколь угодно сложную булеву функцию.
Доказательство функциональной полноты некоторой системы
булевых функций можно осуществлять одним из двух способов:
1) С использованием теоремы о функциональной полноте .
2) С использованием конструктивного подхода .
Теорема о функциональной полноте (Пост - Яблонского).
Для того, чтобы система булевых функций была функционально полной необходимо и достаточно чтобы она содержала хотя бы одну функцию не:
1) cохраняющую константу ноль
2) cохраняющую константу единица
3) линейную функцию
4) монотонную функцию
5) самодвойственную функцию.
Замечательные классы булевых функций.
1. Булева функция называется сохраняющей константу ноль , если на нулевом наборе аргументов она принимает значение равное нулю, то есть f(0,0,0,...,0) = 0;
В противном случае функция относится к классу не cохраняющих константу ноль.
К функциям ,сохраняющим константу ноль относятся
f(x1
,x2
)= x1
v x2
f(x1
,x2
)= x1 *
x2
К функциям не cохраняющим константу ноль относятся
f(x)= и f(x1
,x2
)=x1
~x2 и f(x1
,x2
)=x1
~x2
2.Булева функция называется сохраняющей константу единица , если на единичном наборе аргументов она принимает значение равное единице, то есть f(1,1,1,...,1)= 1;
В противном случае функция относится к классу не cохраняющих константу единица.
К функциям ,сохраняющим константу единица относятся
f(x1
,x2
)= x1
v x2
f(x1
,x2
)= x1 *
x2
К функциям не cохраняющим константу единица относятся
f(x)= и f(x1
,x2
)=x1
Åx2 и f(x1
,x2
)=x1
Åx2
3. Булева функция называется линейной если она представима полиномом Жегалкина первой степени.
В булевой алгебре доказывается теорема о возможности представления любой булевой функции от n переменных с помощью полинома Жегалкина n-ой степени.
В общем случае полином имеет вид :
fn
(x)= K0
ÅK1
x1
Å...ÅKn
xn
Å...
...ÅKn+1
x1
x2
ÅKn+2
x1
x3
Å...ÅKn+l
xn-1
xn
Å...
...
...ÅKn+m
x1
x2
...xn
K0
,K1
,Kn+m
-являются коэффициентами и представляют собой логические константы нуля или единицы.
В алгебре Жегалкина одноименной полином можно считать канонической нормальной формой для булевой алгебры.
Полином Жегалкина является линейным (1-ой степени) если все коэффициенты общего полинома ,начиная с Kn+1
=Kn+2
=...=Kn+m
=0
В отношении функции от 2-х переменных полином Жегалкина имеет вид (линейный): f2
(x)=K0
ÅK1
x1
ÅK2
x2
Примерами линейных функций являются:
y= x1
Åx2
(K0
=0,K1
=K2
=1)
_____
y= x1
~x2
=x1
Åx2
=1Åx1
Åx2
(K0
=K1
=K2
)
y=  =1Åx1
(K0
=K1
=1 ,K2
=0) =1Åx1
(K0
=K1
=1 ,K2
=0)
Примеры нелинейных функций:
y= x1
*x2
____
y= x1
lx2
=x1
*x2
=1Åx1
*x2
4.Булева функция называется монотонной если при возрастании наборов аргументов она принимает неубывающие значения.
A=(a1
,a2
,...,an
)>B=(b1
,b2
,...,bn
)
f(A)³f(B)
Между наборами аргументов А и В имеет место отношение возрастания в том и только том случае , если имеет место отношение не убывания для всех компонент этого набора:
___
ai
³bi
(i=1, n )
и по крайней мере для одной компоненты имеет место отношение возрастания.
Примеры наборов ,для которых имеет место отношение возрастания: (1011)>(0011)
(1011)>(0001)
(0001)>(0000)
Пример несопоставимых наборов (1011)и (0111)
В отношении функции от 2-х переменных несопоставимыми являются наборы (01) и (10)
Пример немонотонных функций: y=
y= x1
Åx2
5.Две булевы функции fn
(x) и gn
(x) называются двойственными если для любых наборов аргументов выполняется равенство
____
fn
(x) =gn
(x) то есть функции f и g на противоположных наборах аргументов х и  принимает противоположные значения . принимает противоположные значения .
Два набора аргументов называются противоположными если любая из их компонент принимает противоположные значения.
x=(0101)  =(1010) =(1010)
Булева функция называется самодвойственной если она является двойственной по отношению к самой себето есть принимает противоположные значения на противоположных наборах аргументов.
Примером самодвойственной функции является : у= 
Примеры не самодвойственных функций: у=х1
*х2
у=х1
vх2
у=х1
Åх2
Принадлежность базовых булевых функций и логических констант к замечательным классам представлена таблицей.
К0
+ сохраняет константу ноль ,- не сохраняет константу ноль
К1
+ сохраняет константу единица ,- не сохраняет константу
Кл
+ линейная ,- нелинейная
Км
+ монотонная , - не монотонная
Кс
+ самодвойственная ,- не самодвойственная
| Функция |
К0
|
К1
|
Кл
|
Км
|
Кс
|
| 0 |
+ |
- |
+ |
+ |
- |
| 1 |
- |
+ |
+ |
+ |
- |
 |
- |
| х1
*х2
|
+ |
+ |
- |
+ |
- |
| х1
vх2
|
+ |
+ |
+ |
- |
| х1
Åх2
|
+ |
- |
+ |
- |
- |
| х1
~х2
|
- |
+ |
- |
| х1
Dх2
|
+ |
- |
| х1
®х2
|
- |
| х1
|х2
|
- |
- |
| х1
¯х2
|
- |
Конструктивный подход к доказательству функциональной полноты некоторой системы булевых функций
.
Подход основан на доказательстве реализуемости функций булева базиса с помощью функций этой системы.
При этом естественно предполагать ,и это действительно так, что булев базис образует функционально полную систему.
Пример :S5
={|}
_ ____
x =x * x= x|x
====
x1
*x2
= x1
*x2
=( x1
|x2
)|( x1
|x2
)
______
x1
vx2
= 1
* 1
* 2
=( x1
|x1
)|( x2
|x2
) 2
=( x1
|x1
)|( x2
|x2
)
Синтез комбинационных схем
.
Понятие
логического
элемента
.
Типовые логические элементы и их обозначения на функциональных схемах
.
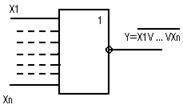
Определение: как правило ,под логическим элементом понимается комбинационная схема ,реализующая некоторую элементарную булеву функцию.
Любой логический элемент характеризуется :
1) Наличием одного или нескольких входов на которые подаются входные сигналы( входные переменные).
2) Наличием выхода ,на котором формируется выходной сигнал
(выходная переменная).
3) Определенной функцией ,которая отображает зависимость выходного сигнала от входных.
К основным типам логических элементов относятся:
1) Инвертор( НЕ)

2) Дизъюнктор (ИЛИ)

3) Конъюнктор (И)

4) Дизъюнкторс отрицанием (ИЛИ - НЕ)
5) Конъюнкторс отрицанием (И - НЕ)

6) Исключительное ИЛИ
(единичный сигнал на выходе имеет место в том и только том случае если на
одном и только одном входе присутствует единичный сигнал)

7) Сумматор по модулю 2

1)Элементы 1,2,3 образуют булев базис.
2)Элементы 1 и 2 или 1 и 3 образует сокращенный(неполный)
булев базис.
3)Элементы 4 или 5 образуют универсальный базис.
4)Элементы 3 и 7 образуют базис Жегалкина.
Функции элементов 6 и 7 совпадают при наличии только двух входов.
Понятие двоичного сигнала
.
Способы его кодирования
.
В связи с использованием двух значений логики в логических схемах как входные ,так и выходные сигналы в этих схемах представляются с помощью так называемого двоичного сигнала - особенностью которого является наличие двух четко различимых уровней ,отождествляемых с нулем и единицей.
В зависимости от того ,какой уровень сигнала сопоставляется с логическим нулем а какой с логической единицей различают два способа кодирования двоичных сигналов:
1)Позитивное кодирование (положительное)
высший уровень сигнала - 1 ,низший - 0
2)Негативное кодирование (отрицательное)
высший уровень сигнала - 0 ,низший - 1
При изменении способа кодирования двоичного сигнала функция одной и той же электронной схемы ,реализующей некоторый логический элемент меняется на противоположную.
Понятие логической системы
.
Типы логических систем
.
Логическая схема представляет собой совокупность логических элементов и связей между ними.
Соединения логических элементов в рамках единой логической системы должны удовлетворять следующим правилам:
1)К любому входу логического элемента могут быть подключены:
a) выход любого другого логического элемента( в частном случае ,того же самого)
б) входной сигнал (входная переменная)
в) логическая константа(0 или 1)
В реальных электронных схемах подача логической константы на вход элемента реализуется либо заземлением либо подключением этого входа обязательно через резистор к шине питания.
2)Выход любого логического элемента схемы может быть подключен к входу другого логического элемента или представлять собой выходной сигнал схемы .В частном случае возможна комбинация того и другого.
Логические схемы разделяются на два типа :
1)Комбинационные
2)Последовательносные
В комбинационных схемах значение выходного сигнала в любой момент времени зависит только от комбинации входных сигналов (в этот же момент времени с учетом задержки распространения сигнала по элементам схемы)
С учетом этой задержки значение выходного сигнала по времени запаздывает на время задержки по сравнению с моментом изменения входных сигналов.
Функционирование комбинационной схемы может быть описано булевой функцией, отражающей зависимость выходного сигнала схемы, как функции от входных сигналов , как аргумент этой функции.
Для комбинационных схем с несколькими выходами эта зависимость отражается системой булевых функций.
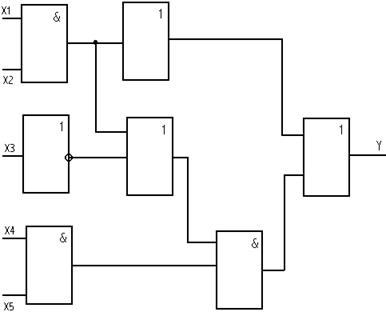
Пример комбинационной схемына элементах булева базиса :
В последовательносных схемах выходные сигналы в любой момент времени зависят не только от комбинации входных сигналов в данный момент времени ,но и от предыстории их изменения ,то есть от последовательности входных сигналов во времени. Как правило последовательносные схемы характеризуются некоторым внутренним строением ,от которого зависит значение выходного сигнала(ов).
Внутреннее состояние такой схемы сохраняется на запоминающих элементах (триггерах) ,в связи с чем ,схемы этого типа называются схемами с памятью.
В общем случае поседовательносная схема представляет собой некоторый цифровой автомат.
Пример последовательносной схемы: (универсальный базис И-НЕ)

Последовательносные схемы характеризуются наличием так называемых петель ,по которым выход некоторого элемента соединяется со входом этого же самого элемента (через другие элементы схемы).
Основные параметры комбинационной схемы.
Основными параметрами комбинационных схем (КС) является стоимость и быстродействие ,как правило при построении абстрактных КС не привязанных к конкретной системе элементов цена схемы определяется в смысле Квайна. Быстродействие схемы ,как правило оценивается задержкой распространения сигналов от входов схемы к ее выходу. Для абстрактных КС эту задержку принято считать в виде : Т=кt,t-задержка на одном логическом элементе,к-максимальное количество логических элементов ,через которые проходит сигнал от входов к выходу.

Как правило задержка схемы сопоставляется с числом уровней этой схемы. Для этой цели все элементы схемы распределяются по уровням. Уровень элемента ,на выходе которого формируется выходной сигнал схемы совпадает с количеством уровней схема и следовательно с ее задержкой.
Для приведенной схемы элементы 1,2,3 относятся к первому уровню.
Элементы 4,5 ко второму уровню.
Элемент 6 к третьему уровню.
Элемент 7 к четвертому уровню.
Задачи анализа и синтеза комбинационных схем
.
В общем виде задача анализа ,комбинационных схем сводится к определению функции ,реализуемой заданной схемой ,в частном случае задача анализа состоит в определении реакции заданной схемы на определенную комбинацию входных сигналов.
Для определения функции схемы целесообразно использовать метод подстановки ,его идея состоит в следующем: Выходы логических элементов обозначаются последовательно продвигаясь от выхода схемы к входам, осуществляют подстановку в выходную функцию промежуточных переменных, как аргумент, до тех пор ,пока в выражении функции все промежуточные переменные не будут заменены на входные переменные:
__
y=y1
v y2
= 4
v y3
y6
=x1
x2
v(y4
v y5
)x4
x5
= 4
v y3
y6
=x1
x2
v(y4
v y5
)x4
x5
=
___
=x1
x2
v(x1
x2
v 3
)x4
x5 3
)x4
x5
Определим реакцию схемы на входной набор.
Например (00000) у=1
Задача синтеза состоит в построении комбинационной схемы по заданному закону функционирования.
При решении этой задачи необходимо учитывать следующие моменты:
1) Синтезируемая схема должна по возможности содержать минимум оборудования. В связи с этим актуальной задачей является минимизация заданной булевой функции. При решении этой задачи целесообразно получить как МДНФ так и МКНФ.
2) Как правило ,синтезируемая схема строится на логических элементах ,принадлежащих некоторому базису. Естественно ,что используемая система элементов должна обладать свойством функциональной полноты ,то есть быть достаточной для построения на ее основе комбинационной схемы ,реализующую любую наперед заданную булеву функцию. Такими функционально полными системами логических элементов являются: 1.{И,ИЛИ,НЕ} 2.{И,НЕ} 3.{ИЛИ,НЕ} 4.{И-НЕ} 5.{ИЛИ-НЕ} 6.{И,М2}
3) Как правило при решении задачи синтеза стараются добиться экстремального значения одного из параметров схемы :минимум цены или максимум быстродействия (минимум задержки).В тех случаях ,когда критерием эффективности схемы является минимум цены по Квайну над минимальными формами проводят дополнительные преобразования ,путем решения задач факторизации и возможно декомпозиции булевой функции. Как правило минимальная форма не дает абсолютного минимума стоимости ,чего можно добиться решением задач факторизации и декомпозиции. Если критерием эффективности схемы является минимальная задержка ,то следует иметь в виду ,что факторное преобразование и декомпозиция булевой функции в общем случае уменьшает цену схемы и увеличивает ее задержку. В более сложном случае схема оптимизируется по одному из показателей при наличии ограничения на второй. Примером подобной постановки задачи синтеза является: Синтезировать схему с минимальной ценой по Квайну ,чтобы ее задержка не превышала 4t.
4) Необходимо учитывать ,в каком виде представлены входные сигналы схемы: только в прямом или и в прямом и в обратном. В первом случае строится комбинационная схема с однофазными входами. Во втором случае с парафазными. Вреальных комбинационных схемах входные сигналы представляют собой значение выходов регистров. Например при построении комбинационного сумматора входные сигналы снимаются с регистров слагаемого. При интегральной реализации регистров в виде СИС в целях минимизации числа выходов выходные сигналы регистров как правило представляются только в прямом виде ,что делает актуальными схемы с однофазными входами.
5) При построении схем в реальной системе элементов необходимо учитывать ряд конструктивных ограничений ,основными из которых являются:
а) Коэффициент объединения по входу, который представляет собой ограничение на число входов в элемент. Может принимать значения 2,3,4,8,16.
б) Коэффициент разветвления по выходам который определяет максимальное число логических элементов, которые можно подключить к выходу элемента в условиях его нормального функционирования. Этот коэффициент определяет нагрузочную способность. Варьируется от 10 до 30.
6) В реальных системах элементов однотипные элементы объединяются в модули ,реализуемые одной интегральной схемой с малым уровнем интеграции(МИС). В связи с этим при построении схем в реальной системе элементов необходимо минимизировать не столько число элементов и входов в них сколько число модулей ,из которых компонуется схема.
7) Как правило в большинстве реальных систем элементов наряду с простыми логическими элементами используются также сдвоенные элементы реализующие составную булеву функцию. Типичным примером может служить элемент И-ИЛИ-НЕ.
8) В реальных системах элементов как правило используется значительное разнообразие логических элементов, относящихся к разным базисам. Тем не менее построение схемы в рамках определенного базиса является достаточно актуальной задачей, так как позволяет уменьшить номенклатуру используемых элементов.
Построение комбинационных схем (КС) по минимальным нормальным формам в различных базисах
.
1) Булев Базис (И, ИЛИ, НЕ)
_ _ _ _ _ _ _
y=x1
x2
x3
vx1
x2
x4
vx1
x5
vx6
(МДНФ)
-------- ------- -----
и (3) и (3) и (2)
Схема с парафазными входами

SQ
=3+3+2=12 Sa
<SQ
<Sb
Sa
=9 Sb
=9+4=13
В общем случае задержка Т=2t (схема 2-х уровневая).
При построении схемы по МКНФ элементами 1-го уровня будут ИЛИ, а 2-го И.
Схема с однофазными входами

SQ
=16 T=3t
В общем случае задержка схемы с однофазными входами составляет 3t.
При построении схемы с однофазными входами целесообразно выбирать такую минимальную форму (если она не единственная) которая содержит наименьшее число инверсий над разными элементами.
При наличии единственной минимальной нормальной формы можно осуществить ее преобразование с использованием закона двойного отрицания и двойственности (Де Моргана)
ººº===ºººº==º===ººººº=--ºººº-º==-ºº
y=x1
x2
x3
v x1
x2
x4
v x4
x5
v x6
= x1
x2
x3
* x1
x2
x4
* x4
x5
* x6
=
-------------------------------------------
=( x1
v x2
v x3
)( x1
v x2
v x4
)( x4
v x5
)* x6
Для реализации этой схемы понадобятся три инвертора.
По сравне6нию с предыдущей схемой цена уменьшается на единицу (SQ
=15). Однако наличие выходного инвертора приведет к увеличению цены схемы T=4t.
2) Сокращенный булев базис (И, НЕ).
При использовании этого базиса необходимо из используемого выражения удалить все операции дизъюнкции, заменив их на конъюнкции и отрицания.
Используя предыдущие преобразования можно построить схему как с парафазными так и с однофазными входами.
Схема с парафазными входами :

SQ
=16 T=4t
При построении схемы на элементах базиса И, НЕ по МДНФ задержка схемы в общем случае составляет 4t. А при использовании однофазных входов 5t.
3) Универсальные базисы И-НЕ и ИЛИ-НЕ (см. Практику).
Задача факторизации (факторного преобразования) булевой функции
.
Факторизация булевой функции сводится к вынесению за скобки общих частей термов, что, как правило, приводит к уменьшению цены синтезируемой схемы.
_ _ _ _ _ _ _ _ _ _ _ _
y=x1
x2
x3
v x1
x2
x4
v x4
x5
v x6
= x1
x2
(x3
v x4
)v x4
x5
v x6
=
SQ
=12 SQ
=10 T=3t
_ _ _ _ _ _ _ _ _
= x1
(x2
x3
v x2
x4
v x5
)vx6
= x1
(x2
(x3
v x4
)v x5
)vx6
T=4t SQ
=11 T=5t SQ
=10
Решение задачи факторизации приводя к уменьшению цены схемы увеличивает ее задержку.
_ _ _ _ _
1) y= x1
x2
(x3
v x4
)v x4
x5
v x6
SQ
=10 T=3t
_ _ _ _
2) y= x1
(x2
(x3
v x4
)v x5
)vx6
T=5t SQ
=10
В тех случаях, когда схема синтезируется при ограничении на число входов в элементы, равное 2, предпочтение следует отдавать скобочной форме 2.
1)

SQ
=10 T=3t

T=3t SQ
=10 Квх
=2
2)

T=5t SQ
=10 Квх
=2
Схема построенная по схеме 2 удовлетворяет ограничению на число входов и является более предпочтительной по сравнению со схемой 1 по критерию цены схемы, а по критерию минимальной задержки - лучше схема 1.
Пример факторного преобразования для МКНФ
_ _ _ _
y=(x1
vx2
vx3
)(x1
vx2
vx4
)(x1
vx5
)= SQ
=11
_ _ _
=( x1
vx2
vx3
x4
)(x1
vx5
)= SQ
=9
_
=x1
v(x2
vx3
)( x2
vx4
) x5
= SQ
=9
_ _
= x1
v(x2
vx3
x4
) x5
= SQ
=8
Оценка эффекта факторизации
.
Этот эффект характеризуется разностью цен схемы до и после факторизации.
Можно показать, что для однократной факторизации ее эффект определяется выражением :
DSQ
= SQ
до
- SQ
после
=m(k-1)+q-D ,
где m - количество букв, выносимых за скобки;
k - количество термов, из которых происходит вынесение. q -количество термов, в которых после вынесения осталась одна буква (q£k);
D=1, если вынесение осуществляется из всех термов;
D=2, если не из всех.
Для эффективного решения задачи факторизации необходимо учитывать следующий момент :
1) Приналичии у булевой функции нескольких минимальных форм целесообразно выбрать из них такие, для которых применение факторизации даст выигрыш в цене схемы.
2) При минимизации не полностью определенной булевой функции может оказаться, что максимальный эффект за счет факторизации дает нормальная форма, не являющаяся минимальной.
Пример :

|10x1 _ _
cmin
(f)=|xx10 МДНФ y=x3
x4
vx1
x2
x4
SQ
=7
|10x1 _ _ _
cmin
(f)=|101x ДНФ y= x1
x2
x4
vx1
x2
x3
= x1
x2
(x3
v x4
) SQ
=5
В некоторых случаях максимального эффекта за счет факторизации можно достичь путем расширения термов МНФ с применением законов товтологии
МДНФ y=x1
x2
x3
vx1
x2
x4
vx1
x3
x5
x6
vx2
x4
x5
x6
= SQ
=18
= x1
x2
(x3
v x4
)v x5
x6
(x1
x3
v x2
x4
)= SQ
=16
= x1
x2
(x1
x3
v x2
x4
)v x5
x6
(x1
x3
v x2
x4
)= SQ
=20
=(x1
x3
v x2
x4
)( x1
x2
v x5
x6
) SQ
=14
Построение одновыходных схем
.
Декомпозиция булевых функций
.
Задача декомпозиции булевой функции в общем случае состоит в таком разделении множества ее аргументов на ряд подмножеств, при котором можно выразить исходную функцию f(x) через вспомогательную промежуточную функцию j(z), где zÌx.
В частном случае имеет место так называемая простая разделительная декомпозиция, при которой множество аргументов x разделяется на два непересекающихся подмножества (z,w®(zÇw=j;zÈw=x)) и приведение исходной функции к виду f(x)=f(j(z,w)).
Пример :f3
(x)=V(1,2,4,7)
(f=1)

z=(x2
x3
) W={x1
}
_ _
j(z)=x2
x3
vx2
x3
_ _
f(x)=x1
j(z)vx1
j(z) SQ
=13

SQ
=13 T=5t
Схема базиса Жигалкина
.

SQ
=4 T=2t
Применение декомпозиции там, где он уместно, во многих случаях позволяет уменьшить цену синтезируемой схемы.
_ _ _ _ _ _ _ _ _ _
МДНФ y=x1
x2
x3
x4
vx2
x5
vx3
x5
vx4
x5
=x1
x2
x3
x4
vx5
(x2
vx3
vx4
)
SQ
=14
_
j(z)=x2
vx3
vx4
___ _
f(x)=x1
*y(z)vx5
*j(z) SQ
=10
Синтез многовыходных комбинационных схем
.
МКС представляется в виде обобщенного «черного ящика»

Закон функционирования МКС представляется в виде системы булевых функций
|y1
=f1
(x1
...xn
)
|y2
=f2
|.
|.
|.
|yn
=fn
Естественным образом, при решении задачи синтеза МКС применяются методы факторизации и возможной декомпозиции, применительно не к одной функции, а к системе.
Минимизация системы Булевых функций
Задача минимизации применительно к системе Булевых функций решается аналогично как для одной функции и сводится к получению минимального покрытия. Для решения этой задачи система приводится к одной функции путем дополнения множества агументов подмножеством вспомогательных переменных, с помощью которых выделяются отдельные функции системы. Количество вспомогательных переменных k³log2
m, m - количество функций.
Пример:

Раздельная минимизация:
y1
Cmin (y1
)=

y2
Cmin (y2
)=

МДНФ:  
При построении схемы по этому выражению, она разлагается на две независимые подсхемы, отдельные для реализаций каждой функции.
Совместная минимизация
Пусть V=0 для у1
; V=1 для y2
 Cmin(y1
,y2
)= Cmin(y1
,y2
)= ; ;
Z= (общий терм) (общий терм)
 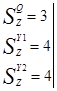 
  
Пример:

V1
V2
=00 y1
V1
V2
=01 y2
V1
V2
=10 y3
V1
V2
=11 y4
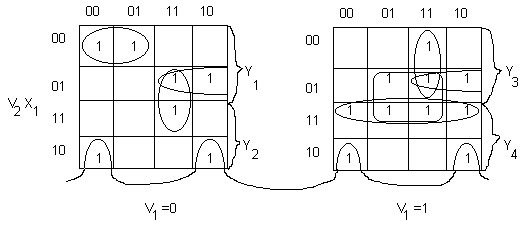
Cmin(S)=
Общие термы:
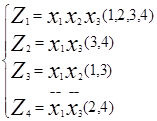 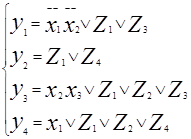
 
При совместной минимизации Булевых функций система в минимальной форме может оказаться, что некоторые термы поглощаются другими, т.е. после получения минимальной формы необходимо исключить поглощаемые термы.
После получения минимального покрытия при записи минимальных форм с начала выделяются термы, общие для нескольких функций и обозначаются вспомогательными функциями (Z1
-Z4
).
В целях удобства рядом с каждым общим термом рекоммендуется проставить его принадлежность.
Далее выписываются минимальные формы для отдельных функций с учетом их собственных термов и общих термов, принадлежащих данной функции. При наличии незадействованных комбинаций вспомогательных переменных все наборы аргументов для них являются безразличными.
Пример:


Сmin(S)=
Для большого числа функций и их аргументов применение карт Карно для совместной минимизации выглядит затруднительным. В этом случае можно использовать следующие подходы:
1. Применение машинных методов
2. Раздельная минимизация и использование карт Карно.
3. Выделение подмножеств из функций системы для их совместной минимизации.
Факторизация системы Булевых функций
Применительно к системе задача факторизации состоит в выделении общих термов или их частей для отдельных функций системы с целью уменьшения цены схемы. Сходная задача уже решается при совместной минимизации функций системы, но совместная минимизация не исключает применение дальнейшей факторизации. Особенно актуальной задачей факторизации становятся при раздельной минимизации функций системы. Совместная факторизация не исключает рпаздельной минимизации в рамках каждой функции.
МДНФ:
  
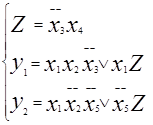  
  
Порядок проведения двух видов факторизации совместной и раздельной в большинстве случаев безразличен.
Декомпозиция системы Булевых функций
Декомпозиция системы Булевых функций - выражение одних функций через другие.
Пример:

| a |
b |
p |
s |
q |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
Однофазные входы
Раздельная минимизация


  
Раздельная факторизация
  
Совместная факторизация
 , ,   

   
  

Совместная минимизация

Cmin=
V=0, S
V=1, q

Арифметические основы ЭВМ
.
Представление чисел в ЭВМ.
Вопросы:
1) Понятие системы счисления.
2) Позиционная и непозиционная системы счисления их отличия и примеры.
3) Понятие основания системы счисления.
4) Понятие веса разряда.
5) Подход к выбору оптимального основания системы счисления (по Савельеву).
6) Обоснования использования в ЭВМ двоичной системы счисления.
7) Правила перевода целых и дробных чисел из одной системы счисления в другую.
8) Двоичная, восьмеричная, шеснадцетиричная системы счисления.
На самостоятельную проработку.
Классификация данных используемых в ЭВМ.
Информация с которой работает ЭВМ в принципе можно разделить на три вида:
1) Команды.
2) Адреса.
3) Данные.
Как правило адресная информация представлена в самих командах ,но прикосвенной адресации адрес может находиться либо в регистре либо в ячейке памяти.
Дерево классификации данных.
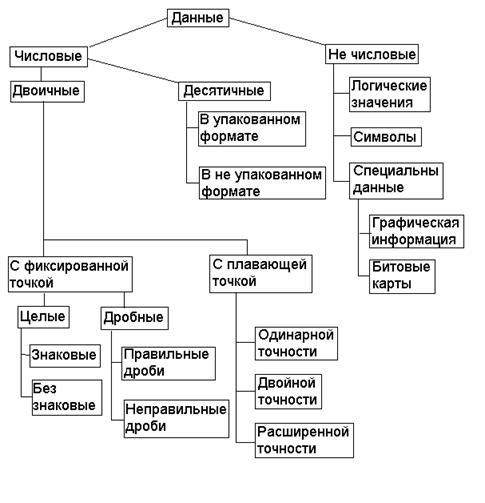
Достаточно широко используется термин аппаратная поддержка данных. Принято считать что данные некоторого типа и определенных форматов являются аппаратно поддерживаемыми в конкретной ЭВМ если в системе команд процессора имеются команды для обработки данных данного типа в соответствующих форматах. Для нечисловых данных основных типов поддержка осуществляется на уровне системных команд. Для логических значений в которых смысловое содержание относится к каждому биту поддержка осуществляется на уровне логических команд: AND,OR,XOR,NOT.
Символьные данные поддерживаются на уровне команд преобразования символов, а также на уровне команд обработки строк.
В ПЭВМ символьные данные представляются в коде ASCII. Сам по себе этот код является семи битным ,но для удобства он расширен до восьми битного с добавлением в наго букв национального алфавита.
Числовые данные естественно поддерживаются на уровне арифметических команд. В связи с разделением чисел на двоичные и десятичные для их обработки используется соответствующая арифметика. В зависимости от формы представления двоичных чисел используется два вида двоичной арифметики.
1) Двоичная целочисленная арифметика.
2) Арифметика с плавающей запятой.
Десятичные числа представляются в двоично-кодированном виде ,в котором любая десятичная цифра представляется в естественном двоичном коде, который принято называть :
8-4-2-1
9 - 1001,8 - 1000,7 - 0111,...,1 - 0001.
В упакованном формате в каждом байте содержится две десятичные цифры ,в не упакованном одна. В ПЭВМ неупакованный формат представляется ASCII-кодом десятичных цифр ,в котором собственно цифра помещается в младшую тетраду ,а старшая тетрада имеет вид 0011.
Пример : 985
1) Упакованный формат 0000|1001 1000|0101
2) Не упакованный формат 0011|1001 0011|1000 0011|0101
Десятичные числа используются в ЭВМ на этапе ввода данных и вывода результатов. После ввода они преобразуются в двоичную систему ,в которой реализуется обработка данных. На этапе вывода двоичный результат предварительно преобразуется в десятичную форму. Преобразования десятичных чисел в двоичные и обратно может быть реализовано как на аппаратном так и на программном уровне. На аппаратном уровне предполагается наличие в системе команд процессора соответствующих команд преобразования. Так например в IBM/370 имеется две команды : CBD - преобразование двоичного числа в десятичное , CDB - преобразование десятичного в двоичное. В ПЭВМ подобных команд нет и преобразование реализуется на программном уровне, с использованием стандартных процедур. Общей тенденцией в вычислительной технике при решении вопроса о реализации той или иной функции на аппаратном или программном уровне является: аппаратный уровень ,обладая большей стоимостью реализации, обеспечивает и большую скорость реализации этой функции. Классическая схема обработки - десятичный ввод, преобразование в двоичную систему, двоичная обработка, преобразование в десятичную, десятичный вывод - выглядит неоправданной при решении задач с большим объемом обрабатываемых данных и малым объемом обработки. Более целесообразный путь десятичный ввод, десятичная обработка, десятичный вывод. Для реализации подобной схемы поддерживаемой на аппаратном уровне необходимо использование в системе команд процессора десятичной арифметики.
Двоичные числа с фиксированной запятой
.
В зависимости от местоположения фиксированной запятой (справа или слева от числа ) числа с фиксированной запятой делятся на целые и дробные. Дробные числа с фиксированной запятой как таковые в современных ЭВМ не используются ,а используются как часть числа с плавающей запятой в виде его мантиссы . Целые числа делятся на два типа: знаковые и беззнаковые. Это разделение определяется способом интерпретации старшего разряда числа. В знаковых он интерпретируется как знак, а в без знаковых числах как старшая цифра числа. Во многих случаях интерпретация целого числа ,как знакового или без знакового возлагается на программиста, хотя на аппаратном уровне может поддерживаться тот или иной способ интерпретации. Примером подтверждающим это может использоваться парные команды умножения MUL,IMUL и деления DIV,IDIV в процессорах INTEL 80X86. Первая команда из этих пар интерпретирует операнды и результат как без знаковое целое ,а вторая как знаковое. Особенностью представления знаковых целых чисел является использование дополнительного кода. Под дополнительным кодом знакового n- разрядного целого числа понимается следующие выражение:ìx, при x³0
[x] дк
= í
î2x
-|x|, при x<0
Например n=6 число 30 представиться в виде [30] дк
=011110
[-30] дк
=1.000000
011110
100000
В связи с тем ,что значение 2n
не представимо в n - разрядном формате можно осуществлять вычитание из нуля. На этом принципе поддерживаются на аппаратном уровне операция изменения знака числа (NEG) с преобразованием его в дополнительный код. В терминологии по поводу прямого и дополнительного кода существуют некоторые разногласия. Авторы некоторых монографий считают что положительные числа представлены в прямом коде ,а отрицательные в дополнительном. Для общности представления ,как положительных ,так и отрицательных чисел в дополнительном коде правильнее считать что дополнительный код положительного числа совпадает с его прямым кодом. Для отрицательных чисел это несправедливо, так как прямой код отрицательного числа в знаковом разряде содержит единицу ,а в цифровых модуль числа. [-30]пр
= 111110
Использование именно дополнительного кода в представлении знаковых целых чисел можно объяснить простотой реализации в этом коде операции сложения и вычитания которые являются самыми массовыми при решении задач научного комплекса. Что касается операций умножения и деления то при использовании дополнительного кода по сравнению с прямым усложняет алгоритм их реализации но тем не менее разработаны методы для выполнения этих операций в дополнительном коде.
Диапазон предоставления чисел
Диапазон представления знаковых n-разрядных чисел определяется в виде
-2 n-1
£ Х £ 2n-1
-1
1 000...0 0 111...1
n-1 n-1
Для стандартного байтного формата (n=8) диапазон :
-128 £ Xц
зн
£127
Максимальное по модулю отрицательное число оказывается по модулю на единицу больше максимального положительного числа.
В связи с этим применение операции изменения знака к максимальному по модулю отрицательному числу приводит к переполнению формата, так как это число не представляется в области положительных чисел.
Формальным приемом изменения знака числа с соответственным преобразованием его из прямого кода в дополнительный или наоборот является инвертирование всех разрядов числа с добавлением единицы в младший разряд.
Для этой цели можно использовать следующее мнемоническое правило : младшие нули и крайняя правая единица прямого кода сохраняются и в дополнительном, а остальные разряды подлежат инвертированию.
Диапазон представления беззнаковых целых чисел в n- разрядном формате имеет вид :
0£Хц
б
.
зн
£2n
-1
Для стандартного байтного формата (n=8) диапазон :
0£ Xц
зн
£255
Диапазон представления дробных чисел
.
Для правильной n-разрядной двоичной дроби диапазон представления имеет вид
2-
n
£Aдр
пр
£1-2-n
Неправильная дробь содержит обязательную двоичную единицу в целой части. Для неправильной n-разрядной двоичной дроби диапазон представления имеет вид
1£Aдр
непр
£2-2-
(
n
-1)
Числа с плавающей запятой
.
В формате представления чисел с плавающей запятой выделяются 3 части : знак числа (представляется крайне левым битом формата); мантисса числа (представляется в виде правильной или неправильной двоичной дроби); порядок числа (представляется в общем виде как целое число со знаком). Значение числа А с плавающей запятой представляется в виде :
Апз
=(sign A)-1
*Ma
*SPa
где sign A - знак 0 - «+», 1 - «-»
SPa
- порядок числа А, S - основание порядка.
Число с плавающей запятой называется нормализованным, если старшая цифра его мантиссы значащая (не 0), в противном случае число называется не нормализованным.
Основными особенностями представления чисел с плавающей запятой в современных ЭВМ являются :
1) Мантисса числа независимо от его знака представляется в прямом коде
2) Порядок числа представляется не в явном виде как знаковое целое, а со смещением в виде беззнакового целого числа.
Эта особенность облегчает обработку порядка при выполнении арифметических операций. Величина смещения равна либо весу старшего разряда порядка, либо на единицу меньше.Cмещенный порядок принято называть характеристикой числа.
3) В качестве основания порядка используется значение S=16 (ЕС ЭВМ) или S=2 (СМ ЭВМ, IEEE).
4) В подавляющем большинстве случаев принято использование нормализованных чисел с целью повышения их точности.
5) При использовании основания порядка, равного двум, нормализованное число содержит обязательную единицу в старшем разряде мантиссы.
Это позволяет не представлять его в явном видев формате, что позволяет увеличить точность числа. Подобное сокрытие старшего разряда мантиссы называется скрытым разрядом (скрытой единицей).
6) В ЭВМ любого класса для представления чисел с плавающей запятой принято использовать несколько форматов (как правило, чтобы удовлетворить противоречивым требованиям повышения точности чисел и повышения скорости их обработки).
Эти форматы используют наименования :
а) короткий (одинарной точности) - 32 бита;
б) длинный (двойной точности) - 64 бита;
в) расширенный (расширенной точности) - 80 бит для РС и 128 бит для больших ЭВМ.
Переход от короткого формата к расширенному может сопровождаться либо расширением только разрядности мантиссы (ЕС ЭВМ) либо расширением разрядности как мантиссы так и порядка (IEEE).
Диапазон представления чисел с плавающей запятой
.
Его принято определять в отношении модуля нормализованного числа. В общем случае этот диапазон представим в виде :
М а мин
норм
*SРа
мин
£½А пл
норм
½£М Ра макс
*SРа макс
Особенности представления чисел с плавающей запятой в ЭВМ различных классов :
1) ЕС ЭВМ (IBM/370) - ЭВМ общего назначения (Main Frame) числа представляются в трех форматах :
0 1 7 8 21(63, 127)
| знак |
характеристика |
мантисса |
В больших ЭВМ принято нумерацию разрядов в формате производить слева направо. В мини компьютерах и персональных ЭВМ - справа налево.
ХА
=РА
+d ; d=64
0£XA
£127
-64£PA
£63
В связи с тем, что в качестве основания порядка используют S=16 признаком нормализации числа является наличие значащей шестнадцатиричной цифры в старших разрядах мантиссы. Таким образом признаком нормализации числа является наличие хотя бы одной единицы в старшей тетраде мантиссы.
Диапазон представления нормализованной мантиссы
1/16£МА
норм
£1-2-m<1
m - число разрядов мантиссы
В общем случае диапазон представления нормализованной мантиссы в виде правильной дроби при основании порядка S имеет вид :
1/S£MA
H
<1
При выполнении арифметических операций при некоторых соотношениях операндов могут возникать ситуации когда результат операции выходит за пределы диапазона.
Выход за праву границу диапазона - получение очень большого по модулю результата классифицируется как переполнение порядка, за левую - как потеря порядка.
В терминологии стандарта IEEE последняя ситуация называется антипереполнением.
Возникновение особых случаев может привести к останову программы (если эти ситуации не являются замаскированными, то есть прерывания по ним разрешены).
2) СМ ЭВМ (РДР-11, VAX-11)
КФ 31 30 23 22 0
| sign |
характеристика |
мантисса |
В качестве основания порядка S=2. Смещенный порядок (характеристика) занимает 8 разрядов, величина смещения равна весу старшего разряда смещения. В мантиссе используется скрытый разряд.
0£xa
£255
-128£Pa
£127
-1£Ma
H
£1

IEEE
КФ (КВ) 31 30 23 22 0
| sign |
характеристика |
мантисса |
ДФ (ДВ) 63 62 52 51 0
| sign |
характеристика |
мантисса |
РФ (РВ) 79 78 64 63 0
| sign |
характеристика |
мантисса |
Скрытая единица имеет место в коротком и длинном форматах, в расширенном формате она представляется в явном виде. Величина смещения определяется как вес старшего разряда характеристики, уменьшенная на единицу.
КФ: d=27
-1=127; ДФ: d=210
-1=1023; РФ: d=214
-1=16383
При определении диапазона чисео необходимо учитывать, что крайние значения характеристики для всех форматов зарезервированы и не используются для представления обычных чисел.
Максимальное значение характеристики, представленное всеми единицами при положительном знаке зарезервированно для представления значения +¥ (нулевая мантисса) и представление так называемых “не чисел” (NAN). Максимальное значение характеристики используется для преставления -¥,¤, (неопределенность) в старшем разряде единица, в остальных - ноль.
Минимальное значение характеристики, представленное всеми нулями зарезервированно для представления “денормализованных” чисел (положительных и отрицательных) и нуля (всеми нулями формата).
КФ:
1£xa
£254
-126£Pa
£127
1£Ma
H
£2

ДФ: 10-308
<|Ап.з.
|<10308
РФ: 10-4932
<|Ап.з.
|<104932
Точность представления чисел
Вопрос о точность может возникать только в отношении дробных чисел с фиксированной запятой и чисел с плавающей запятой. Точность представления числа в ограниченном формате оценивается абсолютной и относительной погрешностью.
Абсолютная погрешность:  А=А-А*
, где А - точное значение А=А-А*
, где А - точное значение
А*
- машинное представление
 А - знаковая величина А - знаковая величина
Относительная погрешность:
 , иногда , иногда 
Погрешность двоичной дроби
Каждая десятичная дробь представляется в виде бесконечной двоичной дроби, что в условиях ограниченного формата ее представление приводит к погрешности. Максимальная абсолютная погрешность бесконечной двоичной дроби имеет место в том случае, когда все отбрасываемые разряды равны единице.
правильная дробь:
(n-разрядная)
1 1 1 …

Максимальная абсолютная погрешность правильной дроби равна весу ее младшего разряда.


Погрешность представления чисел с плавающей запятой определяется погрешностью их мантиссы как дробного числа.
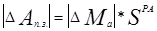

Точность представления чисел с плавающей запятой принято оценивать их максимальные относительные погрешности. Точность определяется в отношении нормализованных чисел.

Эта формула справедлива для мантисс, представленных правильной дробью, а так же неправильной.
Точность представления для коротких форматов в ЭВМ различных типов
ЕС ЭВМ

СМ ЭВМ

IEEE

Часто при проектировании специализированных ЭВМ возникает задача определения формата числа с плавающей запятой исходя из заданных требований по их диапазону и точности представления.
Методы округления чисел с плавающей запятой
Используются для увеличения точности представления чисел и применяются в тех случаях, когда результат операции представленный в ДФ или РФ переписывается из сопроцессора или FPU в память в более коротком формате. Методы округления в РС оговариваются международным стандартом IEEE-754(854). К ним относятся:
1. Округление усечением (разряды не вмещающиеся в формат отбрасываются)
2. Округление к ближайшему (реализуется на основе старшего из отбрасываемых разрядов), непомещающихся в формат, если этот разряд равен единице, то к младшему разряду мантиссы добавляется единица, в противном случае мантисса остается без изменений.
3. Округление к ближайшему большему (к +¥)(для положительных чисел реализуется добавлением единицы к младшему разряду мантиссы; для отрицательных мантисса остается без изменений).
4. Округление к ближайшему меньшему (к -¥) (для положительных -мантисса не меняется; для отрицательных чисел - к ней добавляется единица).
Использование любого метода округления, исключая округление усечением, позволяет уменьшить максимальную относительную погрешность до значения  . При этом максимальная относительная погрешность мантиссы становится равной весу старшего из отбрсываемых разрядов. По умолчанию используется метод округления к ближайшему. Методы округления (к -¥) и (к +¥) используются в “интервальной” арифметике для определения границ полученных результатов в смысле их точности. . При этом максимальная относительная погрешность мантиссы становится равной весу старшего из отбрсываемых разрядов. По умолчанию используется метод округления к ближайшему. Методы округления (к -¥) и (к +¥) используются в “интервальной” арифметике для определения границ полученных результатов в смысле их точности.
Принципы выполнения арифметических операций в ЭВМ.
Основы двоичной арифметики.
Операция сложения целых чисел.
Сложение n- разрядных целых чисел реализуется на основе n- разрядного комбинационного сумматора который может быть построен из модулей одноразрядных сумматоров путем их соединения по цепям переноса.
Не зависимо от способа интерпретации целых чисел знаковое или беззнаковое их сложение осуществляется идентично путем поразрядного сложения с учетом возникающих переносов .Основным отличием сложения знакового и беззнакового является способ фиксации возможного переполнения.
Для беззнаковых чисел переполнение фиксируется при возникновении переноса из старшего разряда .Этот перенос в процессорах 80Х86 фиксируется во флаге CF-carry flag.
Для знаковых чисел фиксация фиксируется во флаге OF-overflow flag.
Таким образом при программировании на Ассемблере после выполнения сложения беззнакового необходимо проверять CF, а после знакового OF.
Использование именно дополнительного кода в представлении знаковых целых чисел позволяет существенно упростить принцип их сложения и вычитания по сравнению с использованием прямого кода.
Примеры сложения: n=6
-32<=Aз<=31
0<=Aб<=63
A+B=C
A= -11 1.10101
B= -20 +1.01100
----------
C= -31 1.00001
зн. беззн.
A=11 0.01011 11 11
B=-20 1.01100 -20 44
-----------
C= -9 1.10111 -9 55(55)
Переполнение при знаковом сложении и способы его фиксации.
Переполнение может получиться только при сложении операндов с одинаковыми знаками.
зн. беззн.
A=17 0.10001 17 17
B=19 0.10011 19 19
----------
C= 1.00100 -28? 36(36)
зн. беззн.
A= -17 1.01111 -17 47
B= -19 1.01101 -19 45
-----------
C= 0.11100 28? 28?(92)
Переполнение при сложении знаковых целых чисел можно фиксировать одним из двух способов:
1) Сравнением знаков операндов и результата (при наличии ++ или - - знаков операндов и - или + соответственно в знаке результата фиксируется переполнение).
2) Сравнение переносов из двух старших разрядов (при наличии одного и только одного переноса фиксируется переполнение).Именно этот способ используется в процессорах корпорации INTEL для установки флага OF.
Операция вычитания целых чисел.
При использовании знаковых чисел операция может быть реализована одним из двух способов:
1) Сведением к сложению путем предварительного изменения знака второго операнда. При использовании дополнительного кода изменение знака предполагает операцию дополнения над ним ,то есть invert,+1.
2) Выполнение прямого(непосредственного) вычитания по аналогии со сложением вычитание выполняется поразрядно начиная с младших разрядов с учетом возникающих межразрядных заемов.
Таблица истинности одноразрядного двоичного вычитателя имеет вид:
ai bi zi-1 ri zi
0 0 0 0 0
0 0 1 1 1
0 1 0 1 1
0 1 1 0 1
1 0 0 1 0
1 0 1 0 0
1 1 0 0 0
1 1 1 0 1
a i - i-й разряд уменьшаемого.
b i - i-й разряд вычитаемого.
z i-1 - заем из предыдущего разряда.
z i - заем в последующий разряд.
Примеры: n=6
зн. беззн.
A= -13 1.10011 -13 51
B= -28 1.00100 -28 36
-----------
C= 0.01111 15(15) 15(15)
A= -28 1.00100 -28 36
B= -13 1.10011 -13 51
-----------
C= 1.10001 -15(-15) 49?
Для беззнакового вычитания результат не корректный .Факт получения не корректного числа объясняется вычитанием из меньшего большего то есть результат должен быть отрицательным. О факте получения отрицательного беззнакового результата свидетельствует заем в старший разряд .Этот заем при выполнении вычитания фиксируется во флаге CF. Если от полученного результата взять дополнение то получается правильный результат равный 15. В связи с этим при наличии заема в старший разряд полученный результат можно интерпретировать как беззнаковый дополнительный код.
Переполнение при вычитании и способы его фиксации.
В операции знакового вычитания переполнение может иметь место только при различных знаках операндов.
Пример: n=6
зн. беззн.
A= -13 1.10011 -13 51
B= 24 0.11000 24 24
----------
C= 0.11011 27(-37) 27(27)
A= 24 0.10011 24 24
B= -13 1.10011 -13 51
-----------
C= 1.00101 -27? 37?
По аналогии со знаковым сложением фиксация переполнения при вычитании может реализоваться двумя способами:
1) Анализ знаков операндов и результата. Если знаки операндов разные и знак результата отличен от знака первого операнда то фиксируется переполнение.
2) Сравнение заемов в два старших разряда. Если один и только один из заемов имеет место то фиксируется переполнение. При наличии обоих заемов или их отсутствии результат вычитания является корректным.
В процессорах INTEL реализован второй способ в соответствии с которым осуществляется установка флага OF.
Сложение и вычитание чисел с плавающей запятой.
Пример:
А=0,527*103 Pa=3
B=0,923*102 Pb=2 B=0,0923*103
C=Ma+Mb=0.6193*103
Операция сложения чисел с плавающей запятой реализуется в виде последовательных этапов:
1) Сравнение порядков.
2) Выравнивание порядков.
3) Сложение мантисс.
4) Нормализация результата.
Некоторые этапы могут быть опущены при выполнении соответствующих условий для предыдущих этапов.
1) Сравнение порядков реализуется по средством вычитания. При этом в целях однозначности принято из Ра вычитать Рb при использовании смещенных порядков осуществляется вычитание характеристики как беззнаковых целых чисел. Естественно что разность характеристик имеет тоже значение что и разность порядков если при вычитании характеристик имеет место заем в старший разряд то результат вычитания отрицательный и представлен в дополнительном беззнаковом коде. Для второго этапа необходимо его преобразование в прямой код.
2) Этот этап опускается при равенстве порядков операндов то есть если: Xa-Xb=0
При выполнении этого этапа всегда операнд с меньшим порядком приводится к большему порядку. Это реализуется сдвигом мантиссы вправо на количество разрядов равное |Xa-Xb| .В данной трактовке понятие разряда зависит от основания порядка. Для ЕС ЭВМ при |Xa-Xb|=2 мантисса сдвигается на 2-а шестнадцатеричных разряда то есть на 8 двоичных. При сдвиге мантиссы операнда с меньшим порядком происходит потеря ее младших разрядов ,что приводит к уменьшению точности в общем случае.
При использовании в мантиссе скрытого старшего разряда при выполнении операций над мантиссой он должен быть восстановлен.
При большом модуле разности порядков может оказаться что мантисса с меньшим порядком полностью выйдет за пределы формата. Этот факт можно учесть для ускорения выполнения операций следующим образом на первом этапе |Xa-Xb| сравнивается с числом разрядов мантиссы и если он оказывается больше то операция завершается путем присвоения результату значения операнда с большим порядком.
3) При сложении мантисс на этом этапе необходимо учитывать что мантиссы операндов независимо от их знаков представлены в прямом коде в котором и реализуется их сложение. Для операндов с одинаковыми знаками осуществляется сложение мантисс в прямом коде с присвоением результату знака первого операнда.
Единственный момент возникающий при сложении мантисс в прямых кодах это возможность переполнения. Переполнение если оно имеет место устраняется на четвертом этапе. Для операндов с разными знаками сложение мантисс заменяют их вычитанием в принципе вместо прямого вычитания можно выполнить их сложение с представлением одной мантиссы в дополнительном коде. Факт выбора мантисс уменьшаемого и вычитаемого при прямом их вычитании или выбора мантиссы представляемой в дополнительном коде при их сложении определяется типом ЭВМ и в рамках одного типа зависит от модели. В принципе могут использоваться следующие подходы: a) Уменьшаемым является мантисса положительного операнда. б) Уменьшаемым является мантисса первого операнда. в) Уменьшаемым является мантисса операнда с большим порядком ,а при равенстве порядков мантисса первого операнда.
Как вычитание так и сложение мантисс как правило реализуется в беззнаковом варианте о знаке суммы следует судить по переносу ,а о знаке разности по заему .
Для каждого из трех способов сложения мантисс с разными знаками используется свой способ формирования знака результата(продумать какой).
Отрицательный результат будет получен в дополнительном коде и требует преобразования в прямой код.
4) Нормализация
Этот этап имеет место только при получении не нормализованного результата.
На предыдущем этапе может быть получен один из двух видов не нормализованного результата.
а) Результат денормализованый влево получается получается при сложении положительных или отрицательных операндов в случае переполнения.
Нормализация производится посредством сдвига мантиссы в право и увеличении порядка на единицу.
Если порядок результата равный порядку большего операнда был максимальным то увеличение на единицу даст особый случай "переполнение порядка".
б) Результат денормализованый вправо получается при сложении операндов с разными знаками при наличии в мантиссе результата старших нулей.
Нормализация производится сдвигом мантисса влево с целью удаления ведущих нулей .Этот сдвиг сопровождается уменьшением порядка что может повлечь "исчезновение порядка"(анти-переполнение).
Вычитание
Операция вычитания чисел с плавающей запятой сводится к сложению путем предварительного изменения знака второго операнда на противоположный.
В связи с тем, что мантисса числа представляется в прямом коде, при изменении знака числа меняется только знаковый разряд, а мантисса остается прежней.
Операция умножения целых чисел и
принципы ее реализации в ЭВМ
Основные положения двоичного умножения
А=13 x
1101
В=11 1011
---------
1101
+ 1101
1101
-------------
10001111=(143)10
Другой метод:
x
1101
1011
--------
1101
+ 1101
1101
------------------
10001111=(143)10
1. Умножение двоичных чисел (как и десятичных) состоит в последовательном умножении множимого на отдельные разряды множителя с суммированием результатов умножения. Результат умножения множимого на один разряд множителя принято называть частичным произведением. Результат умножения двух чисел представляет собой сумму всех частных произведений.
2. Каждое частное произведение либо совпадает с множимым, либо равно 0.
3. Формируемые частные произведения должны быть определенным образом сдвинуты друг относительно друга для их последующего суммирования.
4. Частные произведения можно формировать как начиная от младших, так начиная и от старших разрядов множителя.
5. В общем случае для результата умножения требуется количество цифр равное сумме количества цифр операндов. При одинаковой разрядности операндов: 2n - разрядов.
Особенности реализации умножения в ЭВМ
1. В операционном устройстве для умножения двоичных чисел должен использоваться многоразрядный двоичный сумматор, что предопределяет умножение в виде последовательного многошагового процесса, на каждом шаге которого проводится умножение на один разряд множителя. Сумма частных произведений: СЧП.
Для фиксации этой суммы на каждом шаге необходимо использовать 2n-разрядный процессор, n-разрядного операнда.
Перед началом операции необходимо осуществить сброс этого регистра (установить в “ноль”).
2. На каждом шаге умножения анализируется определенный разряд множителя, и если он равен единице, то на этом шаге производится сложение СЧП с множимым. Если разряд множителя равен нулю, то сложения на данном шаге производится.
3. Любой шаг умножения должен сопровождаться сдвигом множимого относительно неподвижной СЧП: принципиально возможен и подход, при котором множимое остается неподвижным, но происходит сдвиг СЧП.
4. Реализацию умножения принципиально можно начинать как от младшего, так и от старшего разряда множителя.
5. В целях упрощения схемы управления умножением регистр множителя реализуется как сдвигающий, при этом последовательные разряды множителя, на которые производится умножение на каждом шаге, постепенно перемещаются так, что дают возможность связать схему анализа с одним разрядом множителя.
При выполнении умножения начиная от младших разрядом множителя, схема анализа привязывается к младшему разряду регистра множителя, и в этом регистре реализуется сдвиг вправо. При реализации умножения начиная от старших разрядом множителя схема анализа привязывается к старшему разряду регистра множителя и в нем реализуется сдвиг вправо.
6. Для фиксации момента завершения операции, в операционном устройстве умножения должен быть использован счетчик (суммирующий или вычитающий).
7. Так как в реализации умножения можно использовать различные подходы, связанные с тем, от какого разряда множителя начинается умножение, а так же с тем относительно чего сдвигается, можно использовать четыре способа (схемы) умножения.
Способы (схемы) реализации умножения
1. Умножение, начиная с младших разрядов множителя со сдвигом множимого влево.
2. Умножение, начиная с младших разрядов множителя со сдвигом СЧП вправо.
3. Умножение, начиная со старших разрядов множителя со сдвигом множимого вправо.
4. Умножение, начиная со старших разрядов множителя со сдвигом СЧП влево.
Анализ схем:
1. В схемах умножения со сдвигом множимого для его представления требуется 2n-разрядный регистр.
2. А в схеме умножения, начиная с младших разрядов множителя со сдвигом СЧП вправо для представления множимого требуется n-разрядный регистр.
3. А в схеме умножения, начиная со старших разрядов множителя со сдвигом множимого вправо необходимо использовать 2n-разрядный сумматор, связанный по входу с регистром множителя.
4. Четвертая схема требует 2n-разрядного сумматора.
5. Вторая схема - n-разрядного.
В целях минимизации оборудования целесообразно использовать схему 2, на основе которой реализуется умножение практически во всех ЭВМ.
Упрощенная схема операционного устройства для реализации умножения по второму способу

Операция деления и ее реализация в ЭВМ
Особенности двоичного деления
Пример: 130/10
А= 10000010 | 1010
1010 |--------
------------- |01101
0110010
1010
-------------
001010
1010
-----------
1010
1010
Операция двоичного деления сводится к последовательному вычитанию делителя из делимого и остатков на последующих шагах.
1) Под текущим остатком понимается результат полуученый при вычитании делителя из делимого на первом шаге или из предыдущего остатка на последующих шагах.
2) На предварительном шаге делитель совмещается со старшими разрядами делимого ,а затем на каждом шаге сдвигается вправо на одну цифру относительно неподвижного остатка На последнем шаге делитель совмещается с младшими разрядами остатка.
3) Цифры частного вырабатываемые каждом шаге определяются знаком текущего остатка ,для остатка >= 0 цифра частного равна единице ,для остатка < 0 цифра равна нулю.
Особенности реализации деления в ЭВМ.
(по отношению к целым числам)
1) Делимое по сравнению с делителем представляется в удвоенном формате.
2) В качестве результата деления формируется как частное так и остаток .При этом как правило остаток замещает старшие разряды ,а частное младшие.
3) В целях экономии оборудования на каждом шаге осуществляется не сдвиг делителя вправо относительно остатка ,а сдвиг остатка влево относительно неподвижного делителя. При этом делитель совмещается со старшими разрядами делимого ,а далее остатка.
4) При получении отрицательного остатка на каком либо шаге для перехода к следующему шагу требуется восстановление остатка путем сложения с делителем. Подобный метод называется делением с восстановлением остатка .В целях экономии времени деление как правило реализуется в ЭВМ с применением метода без восстановления .В соответствии с этим методом при получении отрицательного остатка он не восстанавливаясь сдвигается влево так же как и положительный однако при этом на следующем шаге производится не вычитание делителя ,а сложение с делителем.
Доказательство:Допустим на i-м шаге получен отрицательный остаток тогда по методу с восстановлением :Ri+1=2(Ri+B)-B
Ri+1 =2Ri +2B-B=2Ri+B
5) При некоторых соотношениях между делимым и делителем может оказаться что частное не помещается в отводимый формат. Подобная ситуация возникает также при делении на 0. Этот особый случай распознается на начальном шаге деления и приводит к прерыванию выполняемой программы по причине ошибки деления.
Деление беззнаковых.
А/В<2^n А-В*2^n<0 из этого неравенства следует что для проверки корректности деления необходимо вычесть делитель из старших разрядов делимого. Если результат вычитания положителен или равен 0 то операция прекращается выходом на прерывание. В остальном беззнаковое деление реализуется по описанным выше принципам так как цифра частного вырабатываемая на каждом шаге деления определяется знаком текущего остатка ,точнее представляет собой инверсию его знакового разряда, целесообразно расширить n-разрядный сумматор дополнительным разрядом для явного представления знака остатка.
Если по завершению всех шагов деления остаток является отрицательным то требуется его восстановление путем сложения с делителем.
Деление знаковых.
IDIV
По аналогии с операцией умножения знаковое деление может быть реализовано одним из двух методов:
1) Метод деления в прямых кодах .
2) Метод деления в дополнительных кодах.
При использовании первого метода отрицательные операнды предварительно преобразуются в прямой код и далее над ними выполняют деление по аналогии с беззнаковым .Знак частного формируется отдельным действием как сумма по модулю два знаков операндов. Знак остатка совпадает со знаком делимого. Исключением из этого правила является нулевой остаток содержащий в знаковом разряде 0.
Отрицательные результаты в конце операции преобразуют из прямого в дополнительный код.
Существенным отличием деления модулей операндов в прямых кодах от беззнакового деления является проверка корректности деления. Действительно модуль n-разрядного знакового числа размещается в (n-1)-разряде в связи с этим условие корректности для деления в прямых кодах имеет вид |A|/|B|<2^(n-1) ; |A|-|B|^(n-1)<0
В соответствии с последним неравенством пробное вычитание модулей с целью проверки корректности должно выполнятся путем совмещения делителя не со старшими разрядами делимого ,а со сдвинутыми на один разряд вправо.
В целях однообразия выполнения пробного вычитания с основным циклом деления в котором делитель совмещен со старшими разрядами остатка делимое предварительно сдвигают на один разряд влево после чего производится пробное вычитание из старших разрядов сдвинутого делимого.
Деление в дополнительных кодах
.
Основное отличие этого метода от предыдущих состоит в том, что операнды вступают в операцию в коде своего представления вместе со знаком. Однако при этом возникает ряд нюансов :
1) Цифры частного, в том числе и знак, формируемые на каждом шаге, определяются не только остатком, но и знаком делителя. При их совпадении цифра частного равна единице, иначе - нулю.
2) Действие выполняемое над текущим остатком на каждом шаге определяется не только этим остатком, но и знаком делителя. При их совпадении выполняется вычитание делителя из старших разрядов делителя,при не совпадении выполняется сложение делителя со старшими разрядами делителя.
3) Коррекция остатка производится в конце операции в том случае, если его знак не совпадает со знаком делимого. Эта коррекция осуществляется действием над остатком, аналогичным основному циклу деления.
4) Коррекция частного выполняется только при отрицательном делимом и нулевом остатке деления и состоит в инкременте (увеличение на единицу) положительного частного и декременте отрицательного.
5) Проверка корректности деления выполняется также как при делении прямых кодов только в случае положительных операндов.
1) A>0, B>0 => A/B<2n-1
A-B*2n-1
<0
2) A<0, B<0 => A/B<2n-1
A-B*2n-1
>0
3) A<0, B>0 => A/B³-2n-1
A/B>-2n-1
A+B*2n-1
+B>0
4) A>0, B>0 => A/B>-2n-1
-1 A+B*2n-1
+B<0
При одинаковых знаках операндов для проверки корректности деления необходимо сдвинуть делимое на 1 разряд влево а затем вычесть делитель из его старших разрядов.
Проверка корректности осуществляется сравнением знака первого остатка со знаком делимого. Если они НЕ совпадают деление корректно, в противном случае - не корректно.
При разных знаках пробное вычитание фактически заменяется сложением.
В этом нет ничего необычного, так как для первого шага в качестве остатка для первого шага фигурирует само делимое и его знак не совпадает со знаком делителя в соответствии с действиями для основного цикла над текущим остатком в этом случае необходимо выполнять сложение с остатком.
В связи с тем, что при разных знаках операндов получается отрицательное, имеющее диапазон, больший на единицу, чем положительное, начальные шаги, связанные с проверкой корректности деления содержат такую последовательность действий :
1) Сложение делимого с делителем, совмещенным с его младшими разрядами. При этом выполняется знаковое расширение делимого на старшие разряды делителя.
2) Сдвиг полученного остатка на один разряд влево.
3) Сложение с делителем, совмещенным со старшими разрядами остатка.
4) Сравнение знака остатка со знаком делимоговыполняется также как и для операндов с одинаковыми знаками.
В связи с тем, что при проверке корректности деления используется знак делимого необходимо при схемной реализации предусмотреть его сохранение до конца операции. По результату пробного вычитания формируется старшая цифра частного, интерпретируемая как знак.
Действительно, при корректном делении получается верный знак частного.
Пример :A=-168 B=-14 n=5
A=1101011000 ; B=10010
Выполняемые действия
| N шага |
обозначения |
A/R (старшие) |
A/C (младшие) |
| 0 |
A
¬
A
B
R0
|
11010
-10101
10010
¾¾¾
00011
sign R0
¹sign B®
|
11000
10000
1000|0
®®
|
| 1 |
¬
R0
B
R1
|
+00111
10010
¾¾¾
11001
sign R1
=sign B
|
000|00
000|01
|
| 2 |
¬
R1
B
R2
|
+10010
10010
¾¾¾
00000
sign R2
¹sign B®
|
00|010
00|010
®®
|
| 3 |
¬
R2
B
R3
|
+00000
10010
¾¾¾
10010
sign R3
=sign B
|
0|0100
0|0101
|
| 4 |
¬
R3
B
R4
|
-00100
10010
¾¾¾
10010
sign R3
=sign B
|
01010
01011
|
псевдо-
коррекция
|
R4
B
R
|
-10010
10010
¾¾¾
00000
|
| коррекция частного |
+01011
1
¾¾¾
01100
|
Приведенный пример иллюстрирует ряд дополнительных нюансов деления в дополнительных кодах :
На четвертом шаге при сдвиге остатка произошло искажение его знака. Выполняемое действие над остатком должно определяться его знаком для предыдущего шага (до сдвига). В схемной реализации этот факт необходимо учитывать путем применения модифицированного кода с удвоенным знаковым разрядом. В связи с этим разрядность регистра для хранения остатка и частного должна быть 2n+1, а разрядность сумматора (сумматора вычитателя) n+1. При получении нулевого остатка на коком либо шаге деления для следующего шага остаток будет равен делителю. При его сдвиге влево он станет равен удвоенному делителю. И после вычитания делителя на следующем шаге он снова станет равен делителю. Таким образом в конце операции после выработки всех цифр частного остаток будет не нулевым, а равным делителю. Если при этом его знак совпадает со знаком делимого, то в соответствии с основным алгоритмом деления он не подлежит коррекции.
Для устранения этого недостатка алгоритма во всех случаях совпадения знака остатка и делимого выполняется попытка так называемой псевдокоррекции. Если после этой коррекции остаток равен нулю, то он является истинным, если же остаток не равен нулю, то требуется его восстановление обратным по сравнению с псевдокоррекцией действием с делителем.
|