Прусаков
Д. В.
«Первая
краевая задача
для уравнения
теплопроводности
в нецилиндрической
неограниченной
области» 1998- 99
уч. г.
14
Введение 3
1.Постановка
задачи 3
2. Оценочный
анализ решения
задачи. 4
2.1. Оценка
решения сверху. 4
2.2. Оценка
решения в виде
интеграла 5
2.3. Выбор интервала
( ) и оценка погрешности 8
3.
Формулировка
результата
в виде теоремы 10
4.
Примеры 11
Заключение 12
СПИСОК
ЛИТЕРАТУРЫ 13
Введение
В ряде случаев
оказывается
невозможным
или неприемлемым
получение
аналитического
решения поставленной
задачи. Использование
основных теорем
и положений
анализа позволяет
получить качественную
картину поведения
функции решения
в заданной
области, оценить
скорость сходимости
решения. Такой
подход широко
реализуется
в областях
техники, где
получение
результата
необходимо
с заданной
точностью.
1.Постановка
задачи
В дипломной
работе рассматривается
задача:
 (З) (З)
0  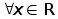 . .
t
 x
x
Требуется
привести пример
оценки решения
задачи (З) в
области
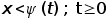 , и исследовать
полученную
оценку при
, и исследовать
полученную
оценку при

2. Оценочный
анализ решения
задачи.
Оценка решения
задачи (З) основывается
на принципе
максимума для
уравнения
теплопроводности
: «Всякое решение
уравнения
 в прямоугольнике
в прямоугольнике
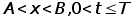 , непрерывное
вплоть до границы,
принимает свои
наибольшее
и наименьшее
значения на
нижних или на
боковых его
границах» [2].
, непрерывное
вплоть до границы,
принимает свои
наибольшее
и наименьшее
значения на
нижних или на
боковых его
границах» [2].
2.1. Оценка
решения сверху.
В области t=t
, x= рассмотрим
решение задачи
:
рассмотрим
решение задачи
:
 ,
V(0,x) = ,
V(0,x) =
 (
x ), x (
x ), x , (1)
, (1)
это
решение имеет
вид
[1]:
v (t, x) =
 .
(2) .
(2)
Зафиксируем
некоторое
 и
перейдем к
исходной системе
координат,
тогда (2) в системе
t=t,
x= и
перейдем к
исходной системе
координат,
тогда (2) в системе
t=t,
x= будет выглядеть
так:
будет выглядеть
так:
V(t, x) =
 (2’)
(2’)
Из принципа
максимума
[2]
заключаем,
что:
U( t, x )
 V( t, x ). (3)
V( t, x ). (3)
Таким образом
задача сводится
к оценке интеграла
(2).
2.2. Оценка
решения в виде
интеграла
Разобьем интервал
 <
x <
x

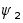 на две части
на две части
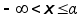 и и
 ,
тогда интеграл
(2’)
запишется
в виде: ,
тогда интеграл
(2’)
запишется
в виде:
V( t, x ) =
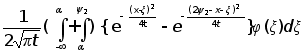 .
(*) .
(*)
Исследуем
знак подинтегрального
выражения,
принимая во
внимание, то
что
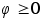 : :
 ;
(а)
;
(а)
 ;
;
 ;
;
где
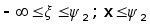 .
.
После проведенного
исследования
видно, что

Использовав
известное
разложение
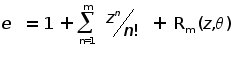 , ,
где Z
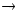 0, 0,
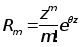 ,
заменим
экспоненты
во втором интеграле
рядами:
,
заменим
экспоненты
во втором интеграле
рядами:
(а)
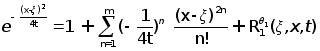 ; ;
(б)
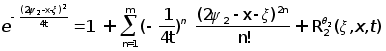 . .
В результате
получим :
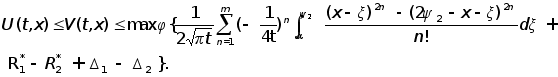
Здесь:
 , ,
 , (4.1)
, (4.1)
 , ,
 .
(4.2) .
(4.2)
Запишем неравенство
(3) в виде, принимая
во внимание
только одно
слагаемое суммы
ряда:
m=1,

U(t, x)
 .
(5)
.
(5)
Выше приведенная
оценка не отражает
качественной
картины и может
быть использована
при дальнейших
исследованиях
задач подобного
вида. ( т .к . фиксированно) фиксированно)
Рассмотрим
другую возможность
оценки неравенства
(3).

пусть

(т.е.
 финитна),
в соответствии
с принципом
максимума: финитна),
в соответствии
с принципом
максимума:
 , (3’)
, (3’)
при

где W-
решение
краевой задачи
(З) с начальными
условиями:
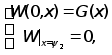

Аналогично,
как и выше

здесь:

Таким образом,

(используем
разложение
в ряд Тейлора)
В
итоге,
 (5.1)
(5.1)
Рассмотрим
два случая:
а)
Пусть

 , ,
тогда в правой
части неравенства
(5.1) третье и четвертое
(3,4) слагаемые
стремятся к
нулю быстрее
любой степени
 , ,
поэтому (5.1) можно
переписать
как:
 (5.2)
(5.2)
б)
Пусть
 тогда: тогда:

где

В
результате
получаем:
 (5.3)
(5.3)
2.3. Выбор
интервала (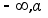 ) и оценка
погрешности
) и оценка
погрешности
Зададим
произвольно
некоторую
константу
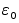 >0,
потребовав
чтобы в (5) >0,
потребовав
чтобы в (5)
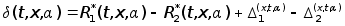 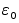 . .
 при
при
 . .
Неравенство
(5) можно только
усилить, если
 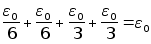 (6)
(6)
Рассмотрим
общий вид
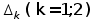 : :
 ; (7)
; (7)
  ,
(7.1)
,
(7.1)
b=x ( k=1 )
, b=2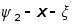 (k=2) (k=2)
 оценка (7.1) эквивалентна
системе неравенств:
оценка (7.1) эквивалентна
системе неравенств:
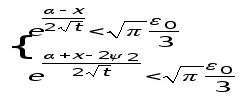 ,
,
откуда:
 .
(8) .
(8)
Т. к. в работе
исследуется
поведение
неравенства
(3) при
 то принимаем
что для некоторого
то принимаем
что для некоторого
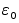 : :
 .
(9) .
(9)
3. Формулировка
результата
в виде теоремы
Обобщая
результаты
всей работы
в целом можно
сформулировать
следующие
теоремы:
1. Пусть
для уравнения
теплопроводности
имеет место
задача
 (З) (З)
 -
гладкая, непрерывно
- дифференцируемая
функция на -
гладкая, непрерывно
- дифференцируемая
функция на
 ,а
функция ,а
функция
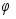 ограничена
на R
: ограничена
на R
:
 . .
Тогда
для любого
сколь малого
числа
 можно указать
число
можно указать
число
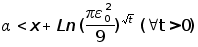 , ,
такое что имеет
место следующая
оценка «сверху»
решения задачи
(З):

Раскрыв квадратные
скобки, получим:
 . .
Пусть в имеет
место задача
(З),
 -
монотонная,
неограниченная,
возрастающая
функция, -
монотонная,
неограниченная,
возрастающая
функция,
 тогда: тогда:
если
 ,
то ,
то
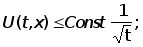
2) если
 то
то

Замечанние:видно,
что оценку
полученную
в теореме 2 можно
получить и при
более слабых
ограничениях

4. Примеры
Пусть
 , ,


 .
.
Заключение
В дипломной
работе произведена
оценка решения
«сверху» для
уравнения
теплопроводности
с движущей
границей по
заданному
закону. Аналогично,
можно получить
оценку решения
«снизу». Для
этого нужно
рассмотреть
ступенчатую
область, в которой
для каждой
ступеньки
решение может
быть получено
согласно 2.1 (2) .
Число таких
ступенчатых
областей необходимо
выбрать таким
образом, чтобы
оценка полученная
снизу была
сравнима с
полученной
выше оценкой.
СПИСОК
ЛИТЕРАТУРЫ
А. Н. Тихонов,
А. А. Самарский,
Уравнения
математической
физики. Изд.
«Наука», М. 1966 (с.
230 -233);
С. К. Годунов,
Уравнения
математической
физики. Изд.
«Наука», М. 1973 .
33-34);
Л. Д. Кудрявцев,
Краткий курс
математического
анализа. Изд.
«Наука», М. 1989.
|