| Лабораторная работа № 1.
Тема:
«Сводка, группировка, статистические таблицы».
Цель
: выявление обобщающих закономерностей, характерных для изучаемой совокупности объектов наблюдения как целостной системы.
Цель исследования—определение уровня успеваемости студентов 1-ого курса, а так же факторов на него влияющих.
В качестве исследуемых признаков я рассматриваю:
1. средний балл по итогам экзаменов за 1-ый курс (баллы).
2. посещаемость занятий в университете на 1-ом курсе.
3. самообразование (дополнительное обучение, курсы) (ч/нед).
4. сон (ч/сутки).
5. пол (м, ж).
6. подготовка к семинарским и практическим занятиям (ч/нед).
7. нравятся ли студенту на 1-ом курсе занятия в университете (да, нет).
Из представленных признаков я выделяю признак-результат—средний балл зачётки по итогам 1-ого курса, так как его значение отвечает цели исследования. Остальные шесть признаков являются признаками-факторами, т. к. они оказывают влияние на признак-результат.
Наблюдение единовременное ауд. 722, 522 СПбГИЭУ. Дата проведения: 03.11.2000г. по форме проведения—опрос. Объектом наблюдения являются 2 группы студентов (1093 и 1094) 2-ого курса. единица наблюдения—студент. Исследование основного массива.
Таблицы с исходными данными.
Таблица 1
| Средний балл зачётки по итогам экзаменов за 1-ый курс (баллы)
|
Посещаемость занятий на первом курсе
|
Самообразование (доп. Курсы) ч/нед
|
Подготовка к семинарским занятиям (ч/нед)
|
Сон (ч/сут)
|
Пол (м, ж)
|
Нравятся ли занятия в университете (да, нет)
|
| 4,7
|
19,5
|
0
|
5
|
7
|
Ж
|
Да
|
| 4,5
|
22
|
2
|
6
|
9
|
Ж
|
Да
|
| 4,2
|
22
|
0
|
2
|
6
|
М
|
Да
|
| 4,3
|
19,5
|
0
|
7
|
7
|
Ж
|
Да
|
| 4,5
|
17,5
|
0
|
3
|
7
|
Ж
|
Нет
|
| 4,2
|
9,5
|
6
|
12
|
10
|
Ж
|
Да
|
| 4,0
|
12,5
|
0
|
5
|
5
|
Ж
|
Да
|
| 4,7
|
22
|
4
|
7
|
6
|
Ж
|
Да
|
| 4,6
|
17,5
|
3
|
4
|
8
|
Ж
|
Да
|
| 4,7
|
9,5
|
0
|
2
|
7
|
Ж
|
Да
|
| 4,5
|
11,5
|
6
|
3
|
7
|
Ж
|
Да
|
| 4,0
|
11,5
|
2
|
3
|
9
|
Ж
|
Да
|
| 4,2
|
19,5
|
4
|
8
|
8
|
Ж
|
Нет
|
| 4,0
|
20,5
|
6
|
9
|
5
|
Ж
|
Да
|
| 3,2
|
9,5
|
0
|
0
|
10
|
М
|
Нет
|
| 4,0
|
17,5
|
0
|
8
|
8
|
М
|
Нет
|
| 3,2
|
14,5
|
0
|
2
|
8
|
М
|
Нет
|
| 3,5
|
14,5
|
0
|
2
|
8
|
М
|
Нет
|
| 4,8
|
22
|
0
|
10
|
10
|
Ж
|
Нет
|
| 4,6
|
8,5
|
0
|
1
|
8
|
М
|
Да
|
| 4,5
|
22
|
0
|
4
|
7
|
Ж
|
Да
|
| 4,5
|
22
|
6
|
2
|
7
|
М
|
Да
|
| 4,2
|
17,5
|
4
|
4
|
9
|
М
|
Нет
|
| 4,5
|
14,5
|
6
|
4
|
10
|
Ж
|
Да
|
| 4,2
|
11,5
|
2
|
2
|
8
|
Ж
|
Нет
|
| 4,8
|
17,5
|
0
|
4
|
9
|
Ж
|
Нет
|
| 4,0
|
10,5
|
0
|
2
|
7
|
Ж
|
Да
|
| 4,2
|
17,5
|
2
|
6
|
5
|
Ж
|
Да
|
| 3,0
|
9,5
|
0
|
0
|
9
|
М
|
Нет
|
| 4,8
|
19,5
|
2
|
2
|
8
|
Ж
|
Да
|
| 4,8
|
19,5
|
2
|
6
|
9
|
Ж
|
Да
|
| 4,3
|
17,5
|
4
|
2
|
7
|
Ж
|
Да
|
| 3,2
|
6,0
|
0
|
0
|
5
|
М
|
Нет
|
| 4,5
|
22
|
2
|
5
|
9
|
Ж
|
Нет
|
| 4,7
|
22
|
4
|
3
|
6
|
Ж
|
Да
|
| 4,2
|
22
|
3
|
5
|
8
|
Ж
|
Да
|
| 4,6
|
9,5
|
0
|
1
|
8
|
Ж
|
Нет
|
| 3,0
|
14,0
|
0
|
2
|
10
|
М
|
Нет
|
| 3,0
|
6,5
|
0
|
5
|
9
|
М
|
Нет
|
| 4,0
|
22
|
2
|
5
|
9
|
Ж
|
Да
|
| 4,7
|
17,5
|
6
|
0
|
10
|
Ж
|
Нет
|
| 3,5
|
11,5
|
0
|
6
|
7
|
М
|
Нет
|
| 4,7
|
22
|
6
|
2
|
5
|
Ж
|
Да
|
| 4,5
|
22
|
0
|
0
|
8
|
Ж
|
Да
|
| 3,2
|
17,5
|
4
|
8
|
9
|
Ж
|
Да
|
| 4,8
|
22
|
0
|
0
|
5
|
М
|
Да
|
| 3,2
|
9,5
|
0
|
5
|
10
|
М
|
Да
|
| 4,5
|
17,5
|
0
|
3
|
10
|
Ж
|
Да
|
| 3,0
|
14,5
|
5
|
3
|
7
|
М
|
Нет
|
| 4,7
|
11,5
|
5
|
3
|
7
|
М
|
Нет
|
Структурные группировки.
1 группировка.
Таблица 2
| Средний балл по итогам экзаменов за 1 курс, баллы
|
Число студентов
|
% к итогу
|
Fi
|
| [3-3,5]
|
9
|
18
|
9
|
| [3,5-4]
|
3
|
6
|
12
|
| [4-4,5]
|
15
|
30
|
27
|
| [4,5-5]
|
23
|
46
|
50
|
| Итог:
|
50
|
100
|
Для удобства разбиваем вариационный ряд на 4 равных интервала. Величину интервала определяем по формуле:
h = R / n = (X max – X min) / n = (5-3) / 4 = 0,5
гистограмма: кумулята:
    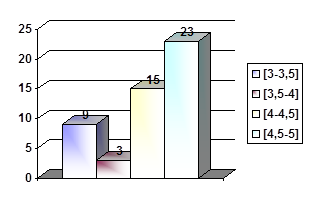
считаем по несгруппированным данным для большей точности:
Х = (4,7 + 4,5 + 4,2 + 4,2 +4,5 + 4,2 + 4,0 + 4,7 + 4,6 + 4,7 + 3,5 + 4,0 + 3,2 + 4,0 + 3,2 + 3,5 + + 4,8 + 4,6 + 4,5 + 4,5 + 4,2 + 4,5 + 4,2 + 4,8 + 4,0 + 4,2 + 3,0 + 3,2 + 4,8 + 4,8 + 4,3 + 4,5 + 4,7 + 4,2 + 4,6 + 3,0 + 3,0 + 4,0 + 4,7 + 3,5 + 4,7 + 4,5 + 3,2 + 4,5 + 4,8 + 3,2 + 3,0 + 4,5 + 4,7) / 50 = 4,27 (балла)
Ме = x0
+ D Ме
(N/2 – F(x0
) / NMe
Me = 4+ 0,5 (25 –12) / 15 = 4,4 (балла)
Мо = х0
+ D Мо
(NМо
– NМо-1
) / (NМо
– NМо-1
) + (NМо
– NМо+1
)
Mo = 4,5 + 0,5 (25-15) / ((23-15) + (23-0)) = 4,6 (балла)
D = å (xi
– x)2
/ n считаем по несгруппированным данным.
D = 0,3 (кв. балла)
bx
= ÖD
bx
= Ö0,3 = 0,55 (балла)
V = bx
/ x × 100%
V = (0,55 / 4,27) × 100% = 128%
R = xmax
– xmin
R = 5 – 3 = 2 (балла)
Вывод: средний балл зачётки по итогам экзаменов за 1-ый курс для данной совокупности составляет 4,27 балла. Т. к. коэффициент вариации является величиной незначительной (128%), можно предполагать, что такой средний балл является типичным для данной совокупности. Наиболее распространённым является балл зачётки 4,6 балла. Средний балл у 50% студентов не больше 4,4 балла.
Группировка 2
Таблица 3
| Посещаемость, ч/нед
|
Число студентов, чел
|
% к итогу
|
Fi
|
| [6-10]
|
9
|
18
|
9
|
| [10-14]
|
8
|
16
|
17
|
| [14-18]
|
15
|
30
|
32
|
| [18-22]
|
18
|
36
|
50
|
| Итог:
|
50
|
100
|
Разбиение на интервалы аналогично группировке 1.
Для несгруппированных данных, значит более точный результат.
Х = å xi
/ n
X = 16, 13 (ч/нед)
Ме = x0
+ D Ме
(N/2 – F(x0
) / NMe
Ме = 14 + 4 (25 – 17) / 15 = 17,3 (ч/нед)
     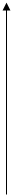 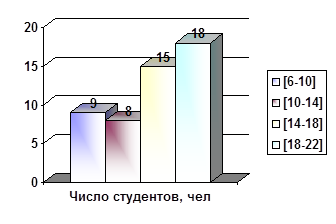
D = å (xi
– x)2
/ n
D = 19,4 ((ч/нед)2
)
bx
= ÖD = 4,4 (ч/нед)
V = bx
/ x × 100% = (4,4 / 16,13) × 100% = 27,2%
R = xmax
– xmin
R = 22 – 16 = 16 (балла)
Вывод: средняя посещаемость в группах составляет 16,13 ч/нед (70% от часов в неделю назначенных расписанием). Коэффициент вариации является величиной незначительной (28,6%), следовательно. Такая средняя посещаемость типична для студентов данной совокупности. Большинство студентов посещало 17,3 ч/нед. Посещаемость занятий у 50% студентов меньше 19 ч/нед, у 50% больше 19 ч/нед.
Группировка 3
Таблица 4
| Самообразование, курсы (ч/нед)
|
Число студентов
|
% к итогу
|
Fi
|
| 0
|
25
|
50
|
25
|
| 2
|
8
|
16
|
33
|
| 3
|
2
|
4
|
35
|
| 4
|
6
|
12
|
41
|
| 5
|
2
|
4
|
43
|
| 6
|
7
|
14
|
50
|
| Итог:
|
50
|
100
|
Полегон частот: кумулята
Х = å xi
ji
/ å ji
= (0 × 25 + 2 × 8 + 3 × 2 + 4 × 6 + 5 × 2 + 6 × 7) / 50 = 1,96 (ч/нед)
NMe
= (n+1) / 2 = 51 / 2 = 25,5
Me = x NMe
; Me = 2 (ч/нед) ; Мо = 0 (ч/нед)
D = å (xi
– x)2
ji
/ å jI
= ((0 – 1,96)2
× 25 + (2 – 1,96)2
× 8 + (3 – 1,96)2
× 2 + (4 – 1,96)2
× 6 + (5 – 1,96)2
× 2 + (6 – 1,96)2
× 7) / 50 = 5,1 (ч/нед)2
bx
= 2,26 (ч/нед)
V = (2,26 / 1,96) × 100% = 115%
R = 6 – 0 = 6 (ч/нед)
Вывод: среднее количество часов, затраченное студентами на самообразование 1,96 ч/нед. Т. к. коэффициент вариации является величиной значительной (115%), то среднее количество является не типичным для данной совокупности. Наиболее распространённым является количество часов самообразования равное 0 ч/нед. Ровно половина из 50 опрошенных студентов не занимались на первом курсе дополнительным самообразованием.
Группировка 4
Таблица 5
| Подготовка к семинарам, ч/нед
|
Число студентов
|
% к итогу
|
Fi
|
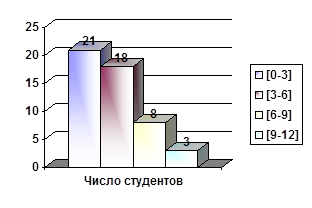
| [0-3]
|
21
|
42
|
21
|
| [3-6]
|
18
|
36
|
39
|
| [6-9]
|
8
|
16
|
47
|
| [9-12]
|
3
|
6
|
50
|
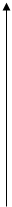 Для удобства разбиваем вариационный ряд на 4 равных интервала. Величину интервала определяем по формуле: h = R / n. h = 3. Для удобства разбиваем вариационный ряд на 4 равных интервала. Величину интервала определяем по формуле: h = R / n. h = 3.
Х = å xi
/ n
Х = 4,08 (ч/нед)
Ме = 3 + 3 (25 – 21) / 18 = 3,6 (ч/нед)
Мо = 0 + 3 (21 – 0) / ((21 – 0) + (21 – 8)) = 1,85 (ч/нед)
D = å (xi
– x)2
/ n
D = 7,2 ((ч/нед)2
)
bx
= 2,7 (ч/нед)
V = (2,7 / 4,08) × 100% = 65,6%
R = 12 – 0 = 12 (ч/нед)
Вывод: среднее время, затраченное на подготовку к семинарским занятиям у студентов на 1 курсе 4,08 ч/нед. Т. к. коэффициент вариации является величиной значительной, то среднее время подготовки является величиной не типичной для данной совокупности студентов. Наиболее распространённым количеством часов на подготовку равно 1,85 ч/нед. Число студентов, занимающихся больше 3,6 ч/нед равно числу студентов, занимающихся подготовкой к занятиям больше 3,6 ч/нед.
Группировка 5
Таблица 6
| Сон, ч/сутки
|
Число студентов
|
% к итогу
|
Fi
|
| 5
|
6
|
12
|
6
|
| 6
|
3
|
6
|
9
|
| 7
|
13
|
26
|
22
|
| 8
|
11
|
22
|
33
|
| 9
|
8
|
16
|
41
|
| 10
|
9
|
18
|
50
|
| Итог:
|
50
|
100
|
 
X = (5 6 + 6 3 + 7 13 + 8 11 + 9 8 + 10 9) / 50 = 7,78 (ч/сут)
NMe
= (n+1) / 2 Me = 8 (ч/сут)
Мо = 7 (ч/сут)
D = å (xi
– x)2
ji
/ å jI
D = 2,4 ((ч/сут)2
)
bx
= 1,55 (ч/сут)
V = (1,55 / 7,78) × 100% = 19,9%
R = 10 – 5 = 5 (ч/сут)
Вывод: среднее значение часов сна 7,78 ч/сутки. Т. к. коэффициент вариации является величиной незначительной (19,9%), то такое среднее значение часов сна является типичным для данной совокупности. Наиболее распространённым является количество часов сна 7 ч/сутки. Количество студентов, которые спят больше 8 ч/сутки равно количеству студентов, спящих меньше 8 ч/сут.
Группировка 6
Таблица 7
| пол
|
Число студентов, чел
|
% к итогу
|
Fi
|
| Ж
|
33
|
66
|
30
|
| М
|
17
|
34
|
50
|
| Итог:
|
50
|
100
|
Вывод: из таблицы видно, что большинство опрошенных студентов женского пола.
Группировка 7
Таблица 8
| Нравятся ли занятия на 1 курсе
|
Число студентов, чел
|
% к итогу
|
Fi
|
| Да
|
30
|
60
|
30
|
| Нет
|
20
|
40
|
50
|
| Итог:
|
50
|
100
|
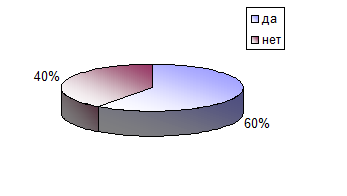
Вывод: из таблицы видно, что большинству студентов данной совокупности нравились занятия на 1 курсе в академии.
Комбинационные группировки.
Таблица 9
| сон
|
Средний балл зачётки
|
Всего
|
| 3
|
3,2
|
3,5
|
4
|
4,2
|
4,3
|
4,5
|
4,6
|
4,7
|
4,8
|
| 5
|
0
|
1
|
0
|
2
|
0
|
0
|
0
|
1
|
1
|
1
|
6
|
| 6
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
2
|
0
|
3
|
| 7
|
1
|
0
|
2
|
1
|
1
|
2
|
2
|
0
|
3
|
1
|
13
|
| 8
|
0
|
1
|
1
|
1
|
3
|
0
|
2
|
0
|
0
|
1
|
11
|
| 9
|
1
|
1
|
0
|
2
|
1
|
0
|
2
|
0
|
0
|
1
|
8
|
| 10
|
2
|
2
|
0
|
0
|
1
|
0
|
2
|
0
|
1
|
1
|
9
|
| Итог:
|
4
|
5
|
3
|
6
|
7
|
2
|
8
|
3
|
7
|
5
|
50
|
Вывод: из таблицы видно, что наиболее крупные элементы расположены близко к побочной диагонали. Следовательно, зависимость между признаками близка к обратной.
Таблица 10
| Посещаемость
|
Средний балл зачётки
|
Всего
|
| 3
|
3,2
|
3,5
|
4
|
4,2
|
4,3
|
4,5
|
4,6
|
4,7
|
4,8
|
| [6-10]
|
2
|
3
|
0
|
0
|
1
|
0
|
0
|
2
|
1
|
0
|
9
|
| [10-14]
|
0
|
0
|
2
|
3
|
1
|
0
|
0
|
0
|
1
|
0
|
7
|
| [14-18]
|
2
|
2
|
1
|
1
|
2
|
1
|
3
|
1
|
1
|
1
|
15
|
| [18-22]
|
0
|
0
|
0
|
2
|
3
|
1
|
5
|
0
|
4
|
4
|
19
|
| Итог:
|
4
|
5
|
3
|
6
|
7
|
2
|
8
|
3
|
7
|
5
|
50
|
Вывод: из таблицы видно, что наибольшие элементы расположены близко к главной диагонали. Следовательно, зависимость между признаками близка к прямой.
Аналитические группировки.
Группировка 1
Таблица 11
Введём обозначения:
1. неудовлетворительная подготовка к занятиям [0-3]
2. удовлетворительная [3-6]
3. хорошая [6-9]
4. отличная [9-12]
| Подготовка к занятиям
|
Число студентов, чел
|
Средний балл зачётки за 1 курс
|
| Неудовлетворительная
|
21
|
3,7
|
| Удовлетворительная
|
18
|
4,3
|
| Хорошая
|
8
|
4,4
|
| Отличная
|
3
|
4,5
|
| Всего:
|
50
|
Вывод: из таблицы видно, что зависимость между фактором и признаком существует.
Группировка 2
Таблица 12
Введём обозначения:
1. 1/3 всех занятий [6-12] ч/нед
2. половина [12-18] ч/нед
3. все занятия [18-22] ч/нед
| Посещаемость занятий
|
Число студентов, чел
|
Средний балл зачётки за 1 курс
|
| 1/3 всех занятий
|
13
|
3,3
|
| половина
|
19
|
4,0
|
| все занятия
|
18
|
4,5
|
| Всего:
|
50
|
Вывод: из таблицы видно, что зависимости между признаком-фактором и признаком-результатом явной нет.
Группировка 3
Таблица 13
| Самообразование
|
Число студентов, чел
|
Средний балл зачётки за 1 курс
|
| Посещали доп. курсы
|
25
|
4,2
|
| Не посещали доп. курсы
|
25
|
4,0
|
Вывод: не наблюдается явной зависимости между признаком-фактором и признаком результатом.
Лабораторная работа № 2
Тема
: Корреляционный анализ, множественная линейная регрессия.
Цель:
выбор оптимальной модели многофакторной регрессии на основе анализа различных моделей и расчитан для них коэффициентов множественной детерминации и среднеквадратических ошибок уравнения многофакторной регрессии.
Корреляционная матрица
Таблица 1
| 0
|
1
|
2
|
3
|
4
|
| 0
|
1
|
0,572
|
0,115
|
0,486
|
0,200
|
| 1
|
0,572
|
1
|
0,218
|
0,471
|
-0,112
|
| 2
|
0,115
|
0,218
|
1
|
0,452
|
-0,048
|
| 3
|
0,438
|
0,471
|
0,452
|
1
|
-0,073
|
| 4
|
-0,2
|
-0,112
|
-0,048
|
-0,073
|
1
|
Где х0
– средний балл зачётки (результат), х1
– посещаемость занятий, х2
– самообразование (доп. курсы), х3
– подготовка к семинарским занятиям, х4
– сон.
Введём обозначения признаков-факторов: 1 – посещаемость занятий на 1 курсе (ч/нед); 2 – самообразование (ч/нед); 3 – подготовка к семинарским и практическим занятиям (ч/нед); 4 – сон (ч/сут); 0 – средний балл зачётки по итогам экзаменов за 1 курс.
Расчётная таблица для моделей многофакторной регрессии.
Таблица 2
| Модель многофакторной регрессии
|
R2
|
E2
|
| 1-2-3-4
|
0,39
|
0,45
|
| 1-2-3
|
0,37
|
0,46
|
| 2-3-4
|
0,23
|
0,51
|
| 1-3-4
|
0,38
|
0,45
|
| 1-2
|
0,33
|
0,47
|
| 1-3
|
0,36
|
0,46
|
| 1-4
|
0,35
|
0,47
|
| 2-3
|
0,20
|
0,52
|
| 2-4
|
0,05
|
0,56
|
| 3-4
|
0,22
|
0,51
|
По трём критериям выбираем оптимальную модель.
1. число факторов минимально (2)
2. max R, R = 0,36
3. min E, E = 0,46
Следовательно, оптимальной моделью является модель 1-3. Значит, признаки-факторы «посещаемость занятий на 1 курсе» и «подготовка к семинарским занятиям» влияют значительнее других факторов на признак-результат.
Среднеквадратическая ошибка уравнения многофакторной регрессии небольшая по сравнению с ошибками, рассчитанными для других моделей многофакторной регрессии.
Составляю для этой модели уравнение регрессии в естественных масштабах.
Х0/1,3
= a + b1
x1
+ b3
x3
Корреляционная матрица.
Таблица 3
| 0
|
1
|
3
|
| 0
|
1,00
|
0,57
|
0,48
|
| 1
|
0,57
|
1,00
|
0,47
|
| 3
|
0,43
|
0,47
|
1,00
|
t0/1,3
= b1
t1
+ b3
t3
    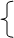 0,57 = b1
+ 0,47b3
0,57 = b1
+ 0,47(0,44 – 0,47b1
) b1
= 0,4 0,57 = b1
+ 0,47b3
0,57 = b1
+ 0,47(0,44 – 0,47b1
) b1
= 0,4
0,44 = 0,47b1
+ b3
b3
= 0,44 – 0,47b1
b3
= 0,25
t0/1,3
= 0,4t1
+ 0,25t3
b1
= (d0
/ dx1
) b1
= (0,47 / 4,4) 0,4 = 0,071
b3
= (d0
/ dx3
) b3
= (0,79 / 2,68) 0,25 = 0,073
a = x0
– b1
x1
– b3
x3
= 4,27 – 0,071 × 16,13 – 0,073 × 4,08 = 2,8
имеем: х0/1,3
=2,8 + 0,071х1
+ 0,073х3
– уравнение линейной множественной регрессии.
 R0/1,3
= Öb1
r01
+ b3
r03 R0/1,3
= Öb1
r01
+ b3
r03
 R0/1,3
= Ö0,4 × 0,58 + 0,25 × 0,48 = 0,6 R0/1,3
= Ö0,4 × 0,58 + 0,25 × 0,48 = 0,6
Вывод: коэффициент b1
говорит о том, что признак-результат—средний балл зачётки за 1 курс на 0,4 долю от своего среднеквадратического отклонения (0,4 × 0,79 = 0,316 балла) при изменении признака-фактора—посещаемости на 1 курсе на одно своё СКО (4,4 ч/нед).
b3
– средний балл зачётки изменится на 0,25 долю от своего СКО (0,25 0,79 = 0,179 балла) при увеличении признака-фактора—подготовки к семинарским занятиям на одно своё СКО (2,68 ч/сут).
Т. к. b1
< b3
, следовательно фактор 1—посещаемость занятий влияет на средний балл зачётки больше, чем фактор 3—подготовка к занятиям.
R2
говорит о том, что 36% общей вариации значений среднего балла зачётки на 1 курсе вызвано влиянием посещаемости и подготовки к занятиям. Остальные 60% вызваны прочими факторами.
R = 0,58 свидетельствует о том, что между посещаемостью занятий и подготовкой к ним и средним баллом зачётки существует заметная линейная зависимость.
Коэффициент b1
говорит о том, что если посещаемость занятий увеличится на 1 ч/нед, то средний балл зачётки увеличится в среднем на 0,071 балла, при условии неизменности всех остальных факторов. b2
говорит о том, что если подготовка к занятиям увеличится на 1 ч/нед, то средний балл зачётки в среднем увеличится на 0,073 балла.
b1
= 0,4 b3
= 0,25
r01
= 0,52
r03
= 0,44
  r13
= 0,47 r13
= 0,47
Граф связи признаков-факторов: х2
– подготовки к семинарским занятиям, ч/нед; х1
- посещаемости занятий, ч/нед с признаком-результатом х0
– средним баллом зачётки по итогам экзаменов за 1 курс.
b1
– мера непосредственного влияния на признак-результат посещаемости занятий.
b3
– мера непосредственного влияния подготовки к занятиям на средний балл зачётки.
r01
= b1
+ r13
b3
, где r01
– общее влияние х1
на r13
b3
– мера опосредованного влияния х1
через х3
на х0.
r01
= 0,4 + 0,47 × 0,25 = 0,52
r03
= b3
+ r31
b1
, где r03
– общее влияние х3
на r31
b1
– мера опосредованного влияния х3
через х1
на х0.
Лабораторная работа № 3.
Тема:
«Дисперсионное отношение. Эмпирическая и аналитическая регрессии.»
Цель: выявление зависимости между признаками-факторами и признаком-результатом.
Таблица с исходными данными.
Таблица 1
| Средний балл зачётки по итогам экзаменов за 1-ый курс (баллы)
|
Посещаемость занятий на первом курсе (ч/нед)
|
Самообразование (доп. Курсы) (ч/нед)
|
Подготовка к семинарским занятиям (ч/нед)
|
| 4,7
|
19,5
|
0
|
5
|
| 4,5
|
22
|
2
|
6
|
| 4,2
|
22
|
0
|
2
|
| 4,3
|
19,5
|
0
|
7
|
| 4,5
|
17,5
|
0
|
3
|
| 4,2
|
9,5
|
6
|
12
|
| 4,0
|
12,5
|
0
|
5
|
| 4,7
|
22
|
4
|
7
|
| 4,6
|
17,5
|
3
|
4
|
| 4,7
|
9,5
|
0
|
2
|
| 4,5
|
11,5
|
6
|
3
|
| 4,0
|
11,5
|
2
|
3
|
| 4,2
|
19,5
|
4
|
8
|
| 4,0
|
20,5
|
6
|
9
|
| 3,2
|
9,5
|
0
|
0
|
| 4,0
|
17,5
|
0
|
8
|
| 3,2
|
14,5
|
0
|
2
|
| 3,5
|
14,5
|
0
|
2
|
| 4,8
|
22
|
0
|
10
|
| 4,6
|
8,5
|
0
|
1
|
| 4,5
|
22
|
0
|
4
|
| 4,5
|
22
|
6
|
2
|
| 4,2
|
17,5
|
4
|
4
|
| 4,5
|
14,5
|
6
|
4
|
| 4,2
|
11,5
|
2
|
2
|
| 4,8
|
17,5
|
0
|
4
|
| 4,0
|
10,5
|
0
|
2
|
| 4,2
|
17,5
|
2
|
6
|
| 3,0
|
9,5
|
0
|
0
|
| 4,8
|
19,5
|
2
|
2
|
| 4,8
|
19,5
|
2
|
6
|
| 4,3
|
17,5
|
4
|
2
|
| 3,2
|
6,0
|
0
|
0
|
| 4,5
|
22
|
2
|
5
|
| 4,7
|
22
|
4
|
3
|
| 4,2
|
22
|
3
|
5
|
| 4,6
|
9,5
|
0
|
1
|
| 3,0
|
14,0
|
0
|
2
|
| 3,0
|
6,5
|
0
|
5
|
| 4,0
|
22
|
2
|
5
|
| 4,7
|
17,5
|
6
|
0
|
| 3,5
|
11,5
|
0
|
6
|
| 4,7
|
22
|
6
|
2
|
| 4,5
|
22
|
0
|
0
|
| 3,2
|
17,5
|
4
|
8
|
| 4,8
|
22
|
0
|
0
|
| 3,2
|
9,5
|
0
|
5
|
| 4,5
|
17,5
|
0
|
3
|
| 3,0
|
14,5
|
5
|
3
|
| 4,7
|
11,5
|
5
|
3
|
Рассматриваю первую пару признаков: признак-фактор—посещаемость занятий на 1 курсе (ч/нед) и признак-результат—средний балл зачётки по итогам экзаменов за 1 курс (баллы). Далее обосную взаимосвязь между ними.
Расчётная таблица №1
Таблица 2
| Посещаемость занятий (ч/нед)
|
Число наблюдений
|
xi
|
yi
|
dyi
|
d2
yi
|
d2
yi
ji
|
yi
- y
|
(yi
–y)2
jI
|
| [6-10]
|
9
|
8,6
|
3,7
|
0,71
|
0,5
|
4,5
|
-0,5
|
2,25
|
| [10-14]
|
8
|
11,5
|
4,1
|
0,38
|
0,14
|
1,12
|
-0,1
|
0,08
|
| [14-18]
|
15
|
16,4
|
3,7
|
1,01
|
1,02
|
15,3
|
-0,5
|
3,75
|
| [18-22]
|
18
|
19,6
|
4,4
|
0,31
|
0,09
|
1,62
|
0,4
|
2,88
|
| Сумма
|
50
|
-
|
-
|
-
|
-
|
22,54
|
-
|
8,96
|
| Средняя
|
-
|
15,3
|
4,0
|
-
|
-
|
5,6
|
-
|
2,24
|
d2
y = (å(yi
–y)2
jI
)
d 2
y = 8,96 / 50 = 0,1792 (балла)2
E2
y= (åб2
yi
jI
) / åjI
E2
y = (4,5 + 1,12 + 15,3 + 1,62) / 50 = 0,4508(балла)2
б2
y = E2
y + d 2
y = 0,4508 + 0,1792 = 0,63 (балла)2
r2
= d 2
y / б2
y = 0,1792 / 0,63 = 0,28 (0,28%)
построение аналитической регрессии.
yx
= a + bx
xy = (åxyjI
) / åjI
= 62,52
б2
x = 19,4 (ч/нед)2
b = (xy – x y) / б2
x = (62,52 – 15,3 × 4,0) / 19,4 = 0,068
a = y – bx = 4,0 – 0,068 × 15,3 = 2,96
Линейное уравнение регрессии зависимости среднего балла зачётки за 1 курс от посещаемости: строим по двум точкам
yx
= 2,96 + 0,068х
- yx
= 2,96 + 0,068 × 6 = 3,358
- yx
= 2,96 + 0,068 × 22 = 4,446
rxy
= (xy – x y) / бx
бy
= 0,37
Корреляционное поле
Эмпирическая линия регрессии
Аналитическая линия регрессии
Распределение среднего балла зачётки за 1 курс по признаку-фактору—посещаемости занятий на 1 курсе.
Вывод: r2
свидетельствует о том, что 28% общей вариации результативного признака вызвано влиянием признака фактора—посещаемостью. Остальные 72% - вызваны влиянием прочих факторов. Можно сказать, что это слабая корреляционная зависимость. Интерпретируя параметр b, предполагаем, что для данной совокупности студентов с увеличением посещаемости занятий на 1 курсе на 1 ч/нед средний балл зачётки увеличивается на 0,068 балла. rxy
говорит о том, что между признаком-результатом и признаком-фактором заметная линейная связь.
Рассматриваю вторую пару признаков:
Расчётная таблица № 2.
Таблица 3
| Подготовка к семинарским занятиям (ч/нед)
|
Число наблюдений
|
xi
|
yi
|
dyi
|
d2
yi
|
d2
yi
ji
|
yi
- y
|
(yi
–y)2
ji
|
| [0-3]
|
20
|
1,2
|
3,78
|
0,63
|
0,39
|
7,8
|
-0,22
|
0,96
|
| [3-6]
|
18
|
4,0
|
4,31
|
0,45
|
0,2
|
3,6
|
0,31
|
1,72
|
| [6-9]
|
9
|
6,8
|
4,46
|
0,28
|
0,07
|
0,63
|
0,46
|
1,9
|
| [9-12]
|
2
|
9,5
|
4,4
|
0,399
|
0,15
|
0,3
|
0,4
|
0,32
|
| Сумма
|
50
|
-
|
-
|
-
|
-
|
2,33
|
-
|
4,9
|
| средняя
|
-
|
3,5
|
4,0
|
-
|
-
|
3,08
|
-
|
1,2
|
d2
y = (å(yi
–y)2
jI
)
d 2
y = 4,9 / 50 = 0,098 (балла)2
E2
y= (åб2
yi
jI
) / åjI
E2
y = 12,33 / 50 = 0,25 (балла)2
б2
y = E2
y + d 2
y = 0,35 (балла)2
r2
= d 2
y / б2
y = 0,098 / 0,35 = 0,28 (0,28%)
r = 0,53
построение аналитической регрессии.
yx
= a + bx
xy = (åxyjI
) / åjI
xy = 15,2
б2
x = 7,2 (ч/нед)2
b = (xy – x y) / б2
x = (15,2 – 3,5 × 4,0) / 7,2 = 0,16
a = y – bx = 4,0 – 0,16 × 3,4
Линейное уравнение регрессии зависимости среднего балла зачётки за 1 курс от подготовки к семинарским занятиям:
yx
= 2,96 + 0,068х
x = 0 y = 3,4
x = 7 y = 4,5
rxy
= (xy – x y) / бx
бy
= (15,2 – 14) / 2,6 = 0,46
Корреляционное поле
Эмпирическая линия регрессии
Аналитическая линия регрессии
Распределение среднего балла зачётки за 1 курс по признаку-фактору—подготовке к семинарским занятиям.
Вывод: r2
свидетельствует о том, что 28% общей вариации результативного признака вызвано влиянием признака фактора—подготовкой к семинарским занятиям. Остальные 72% - вызваны влиянием прочих факторов. Можно сказать, что это слабая корреляционная зависимость. Интерпретируя параметр b, предполагаем, что для данной совокупности студентов с увеличением подготовки к занятиям на 1 курсе на 1 ч/нед средний балл зачётки увеличивается на 0,16 балла. rxy
говорит о том, что между признаком-результатом и признаком-фактором есть умеренная линейная связь.
Рассматриваю третью пару признаков:
Расчётная таблица № 3
Таблица 4
| Самообразование (ч/нед)
|
Число наблюдений
|
xi
|
yi
|
dyi
|
d2
yi
|
d2
yi
ji
|
yi
- y
|
(yi
–y)2
ji
|
| 0
|
25
|
0
|
4,07
|
0,68
|
0,46
|
11,5
|
-0,03
|
0,022
|
| 2
|
8
|
2
|
4,38
|
0,3
|
0,09
|
0,72
|
0,28
|
0,62
|
| 3
|
2
|
3
|
4,40
|
0,2
|
0,04
|
0,08
|
0,3
|
0,18
|
| 4
|
6
|
4
|
4,22
|
0,5
|
0,25
|
1,5
|
0,12
|
0,08
|
| 5
|
2
|
5
|
3,35
|
0,35
|
0,12
|
0,24
|
-0,75
|
1,16
|
| 6
|
7
|
6
|
3,3
|
0,40
|
0,16
|
1,12
|
0,2
|
0,28
|
| Сумма
|
50
|
-
|
-
|
-
|
-
|
15,88
|
-
|
2,34
|
| средняя
|
-
|
1,96
|
4,1
|
-
|
-
|
0,31
|
-
|
0,39
|
d2
y = (å(yi
–y)2
jI
)
d 2
y = 2,34 / 50 = 0,046 (балла)2
E2
y= (åб2
yi
jI
) / åjI
E2
y = 15,88 / 50 = 0,31 (балла)2
б2
y = E2
y + d 2
y = 0,31 + 0,046 = 0,36 (балла)2
r2
= d 2
y / б2
y = 0,046 / 0,36 = 0,13 (13%)
r = 0,36
построение аналитической регрессии.
yx
= a + bx
xy = (åxyjI
) / åjI
xy = 8,22
б2
x = 5,1 (ч/нед)2
b = (xy – x y) / б2
x = (8,22 – 8,036) / 5,1 = 0,032
a = y – bx = 4,1 – 0,032 × 1,96 = 4,03
Линейное уравнение регрессии зависимости среднего балла зачётки за 1 курс от самообразования:
yx
= 2,96 + 0,068х
x = 0 y = 3,4
x = 7 y = 4,5
rxy
= (xy – x y) / бx
бy
= (8,2 – 8,036) / 2,25 × 0,6 = 0,12
Корреляционное поле
Эмпирическая линия регрессии
Аналитическая линия регрессии
Вывод: r2
свидетельствует о том, что 13% общей вариации результативного признака вызвано влиянием признака фактора—самообразованием. Можно сказать, что это очень слабая корреляционная связь. Зная коэффициент b, предполагаем, что для данной совокупности студентов с увеличением самообразования на 1 ч/нед средний балл зачётки увеличивается на 0,032 балла. rxy
говорит о том, что между признаком-результатом и признаком-фактором есть слабая прямая линейная связь.
Министерство Высшего Образования РФ
Санкт-Петербургский Государственный Инженерно-Экономический Университет
Лабораторные работы
По статистике
Студентки 1 курса
Группы 3292
Специальность коммерция
Харькиной Анны.
Преподаватель: Карпова Г. В.
Оценка:
СПб 2001
|