Реферат: Решение задач транспортного типа методом потенциалов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ

Факультет заочно-послевузовского обучения

КУРСОВАЯ РАБОТА

По дисциплине: "Методы оптимизации"

На тему: " Решение задач транспортного типа методом потенциалов "

Воронеж 2003 г.

СОДЕРЖАНИЕ

1. Линейная транспортная задача. 3

2. Математическая модель транспортной задачи. 4

3. Составление опорного плана. 5

4. Распределительный метод достижения оптимального плана. 8

5. Решение транспортной задачи методом потенциалов. 11

Список использованной литературы .. 16

1. Линейная транспортная задача.

Линейные транспортные задачи составляют особый класс задач линейного программирования. Задача заключается в отыскании такого плана перевозок продукции с m складов в пункт назначения n который, потребовал бы минимальных затрат. Если потребитель j получает единицу продукции (по прямой дороге) со склада i , то возникают издержки С _ij . Предполагается, что транспортные расходы пропорциональны перевозимому количеству продукции, т.е. перевозка k единиц продукции вызывает расходы k С _{i j} .

Далее, предполагается, что

где a_i есть количество продукции, находящееся на складе i , и b_j – потребность потребителя j .

Замечание.

1. Если сумма запасов в пунктах отправления превышает сумму поданных заявок то количество продукции, равное 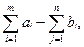остается на складах. В этом случае мы введем "фиктивного" потребителя n +1 с потребностью 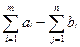и положим транспортные расходы p_{i , n +1} равными 0 для всех i .

2. Если сумма поданных заявок превышает наличные запасы то потребность не может быть покрыта. Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления m + 1 с запасом и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равным нулю.

2. Математическая модель транспортной задачи.

где x_ij количество продукции, поставляемое со склада i потребителю j , а С _{i j} издержки (стоимость перевозок со склада i потребителю j ).

3. Составление опорного плана.

Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы. Например, способ северо-западного угла, способ минимальной стоимости по строке, способ минимальной стоимости по столбцу и способ минимальной стоимости таблицы.

Рассмотрим простейший, так называемый способ северо-западного угла. Пояснить его проще всего будет на конкретном примере:

Условия транспортной задачи заданы транспортной таблицей.

Таблица № 1

Будем заполнять таблицу перевозками постепенно начиная с левой верхней ячейки ("северо-западного угла" таблицы). Будем рассуждать при этом следующим образом. Пункт В₁ подал заявку на 18 единиц груза. Удовлетворим эту заявку за счёт запаса 48, имеющегося в пункте А₁ , и запишем перевозку 18 в клетке (1,1). После этого заявка пункта В₁ удовлетворена, а в пункте А₁ осталось ещё 30 единиц груза. Удовлетворим за счёт них заявку пункта В₂ (27 единиц), запишем 27 в клетке (1,2); оставшиеся 3 единицы пункта А₁ назначим пункту В₃ . В составе заявки пункта В₃ остались неудовлетворёнными 39 единиц. Из них 30 покроем за счёт пункта А₂ , чем его запас будет исчерпан, и ещё 9 возьмём из пункта А₃ . Из оставшихся 18 единиц пункта А₃ 12 выделим пункту В₄ ; оставшиеся 6 единиц назначим пункту В₅ , что вместе со всеми 20 единицами пункта А₄ покроет его заявку. На этом распределение запасов закончено; каждый пункт назначения получил груз, согласно своей заявки. Это выражается в том, что сумма перевозок в каждой строке равна соответствующему запасу, а в столбце - заявке. Таким образом, нами сразу же составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является опорным решением транспортной задачи:

Таблица № 2

Составленный нами план перевозок, не является оптимальным по стоимости, так как при его построении мы совсем не учитывали стоимость перевозок С _ij .

Другой способ - способ минимальной стоимости по строке - основан на том, что мы распределяем продукцию от пункта A_i не в любой из пунктов B_j , а в тот, к которому стоимость перевозки минимальна. Если в этом пункте заявка полностью удовлетворена, то мы убираем его из расчетов и находим минимальную стоимость перевозки из оставшихся пунктов B_j . Во всем остальном этот метод схож с методом северо-западного угла. В результате, опорный план, составленный способом минимальной стоимости по строке выглядит, так как показано в таблице № 3.

При этом методе может получиться, что стоимости перевозок C_ij и C_ik от пункта A_i к пунктам B_j и B_k равны. В этом случае, с экономической точки зрения, выгоднее распределить продукцию в тот пункт, в котором заявка больше. Так, например, в строке 2: C₂₁ = C₂₄ , но заявка b₁ больше заявки b₄ , поэтому 4 единицы продукции мы распределим в клетку (2,1).

Таблица № 3

Способ минимальной стоимости по столбцу аналогичен предыдущему способу. Их отличие состоит в том, что во втором способе мы распределяем продукцию от пунктов B_i к пунктам A_j по минимальной стоимости C_ji .

Опорный план, составленный способами минимальных стоимостей, обычно более близок к оптимальному решению. Так в нашем примере общие затраты на транспортировку по плану, составленному первым способом F₀ = 1039, а по второму F₀ = 723.

Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными . Их число должно равняться m + n - 1. Необходимо отметить также, что встречаются такие ситуации, когда количество базисных клеток меньше чем m + n - 1. В этом случае распределительная задача называется вырожденной. И следует в одной из свободных клеток поставить количество перевозок равное нулю. Так, например, в таблице № 3:

m + n - 1 = 4 + 5 - 1 = 8,

а базисных клеток 7, поэтому нужно в одну из клеток строки 3 или столбца 2 поставить значение “0”. Например в клетку (3,5).

Составляя план по способам минимальных стоимостей в отличии от плана по способу северо-западного угла мы учитываем стоимости перевозок C_ij , но все же не можем утверждать, что составленный нами план является оптимальным.

4. Распределительный метод достижения оптимального плана.

Теперь попробуем улучшить план, составленный способом северо-западного угла. Перенесем, например, 18 единиц из клетки (1,1) в клетку (2,1) и чтобы не нарушить баланса перенесём те же 18 единиц из клетки (2,3) в клетку (1,3). Получим новый план. Подсчитав стоимость опорного плана (она ровняется 1039) и стоимость нового плана (она ровняется 913) нетрудно убедиться, что стоимость нового плана на 126 единиц меньше. Таким образом, за счёт циклической перестановки 18 единиц груза из одних клеток в другие нам удалось понизить стоимость плана:

Таблица №4

На этом способе уменьшения стоимости в дальнейшем и будет основан алгоритм оптимизации плана перевозок. Циклом в транспортной задаче мы будем называть несколько занятых клеток, соединённых замкнутой, ломанной линией, которая в каждой клетке совершает поворот на 90°.

Существует несколько вариантов цикла:

1.) 2.) 3.)

Нетрудно убедиться, что каждый цикл имеет чётное число вершин и значит, чётное число звеньев (стрелок). Условимся отмечать знаком + те вершины цикла, в которых перевозки необходимо увеличить, а знаком - , те вершины , в которых перевозки необходимо уменьшить. Цикл с отмеченными вершинами будем называть означенным. Перенести какое-то количество единиц груза по означенному циклу, это значит увеличить перевозки, стоящие в положительных вершинах цикла, на это количество единиц, а перевозки, стоящие в отрицательных вершинах уменьшить на то же количество. Очевидно, при переносе любого числа единиц по циклу равновесие между запасами и заявками не меняется: по прежнему сумма перевозок в каждой строке равна запасам этой строки, а сумма перевозок в каждом столбце - заявке этого столбца. Таким образом, при любом циклическом переносе, оставляющем перевозки неотрицательными допустимый план остаётся допустимым. Стоимость же плана при этом может меняться: увеличиваться или уменьшатся. Назовём ценой цикла увеличение стоимости перевозок при перемещении одной единицы груза по означенному циклу. Очевидно, цена цикла ровна алгебраической сумме стоимостей, стоящих в вершинах цикла, причём стоящие в положительных вершинах берутся со знаком + , а в отрицательных со знаком - . Обозначим цену цикла через g . При перемещении одной единицы груза по циклу стоимость перевозок увеличивается на величину g . При перемещении по нему k единиц груза стоимость перевозок увеличиться на k g . Очевидно, для улучшения плана имеет смысл перемещать перевозки только по тем циклам, цена которых отрицательна. Каждый раз, когда нам удаётся совершить такое перемещение, стоимость плана уменьшается на соответствующую величину k g . Так как перевозки не могут быть отрицательными, мы будем пользоваться только такими циклами, отрицательные вершины которых лежат в базисных клетках таблицы, где стоят положительные перевозки. Если циклов с отрицательной ценой в таблице больше не осталось, это означает, что дальнейшее улучшение плана невозможно, то есть оптимальный план достигнут.

Метод последовательного улучшения плана перевозок и состоит в том, что в таблице отыскиваются циклы с отрицательной ценой, по ним перемещаются перевозки, и план улучшается до тех пор, пока циклов с отрицательной ценой уже не останется. При улучшении плана циклическими переносами, как правило, пользуются приёмом, заимствованным из симплекс-метода: при каждом шаге (цикле) заменяют одну свободную переменную на базисную, то есть заполняют одну свободную клетку и взамен того освобождают одну из базисных клеток. При этом общее число базисных клеток остаётся неизменным и равным m + n - 1 . Этот метод удобен тем, что для него легче находить подходящие циклы.

Можно доказать, что для любой свободной клетке транспортной таблице всегда существует цикл и притом единственный, одна из вершин которого лежит в этой свободной клетке, а все остальные в базисных клетках. Если цена такого цикла, с плюсом в свободной клетке, отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза k , которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки).

Применённый выше метод отыскания оптимального решения транспортной задачи называется распределённым; он состоит в непосредственном отыскании свободных клеток с отрицательной ценой цикла и в перемещении перевозок по этому циклу.

Распределительный метод решения транспортной задачи, с которым мы познакомились, обладает одним недостатком: нужно отыскивать циклы для всех свободных клеток и находить их цены. От этой трудоёмкой работы нас избавляет специальный метод решения транспортной задачи, который называется методом потенциалов.

5. Решение транспортной задачи методом потенциалов.

Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены.

Пусть имеется транспортная задача с балансовыми условиями

Стоимость перевозки единицы груза из A_i в B_j равна C _ij ; таблица стоимостей задана. Требуется найти план перевозок x_ij , который удовлетворял бы балансовым условиям и при этом стоимость всех перевозок бала минимальна.

Идея метода потенциалов для решения транспортной задачи сводиться к следующему. Представим себе что каждый из пунктов отправления A_i вносит за перевозку единицы груза (всё равно куда) какую-то сумму a _i ; в свою очередь каждый из пунктов назначения B_j также вносит за перевозку груза (куда угодно) сумму b _j . Эти платежи передаются некоторому третьему лицу (“перевозчику“). Обозначим a _i + b _j = č _ij ( i =1.. m ; j =1.. n ) и будем называть величину č _ij “псевдостоимостью” перевозки единицы груза из A_i в B_j . Заметим, что платежи a _i и b _j не обязательно должны быть положительными; не исключено, что “перевозчик” сам платит тому или другому пункту какую-то премию за перевозку. Также надо отметить, что суммарная псевдостоимость любого допустимого плана перевозок при заданных платежах (a _i и b _j ) одна и та же и от плана к плану не меняется.

До сих пор мы никак не связывали платежи (a _i и b _j ) и псевдостоимости č _ij с истинными стоимостями перевозок C _ij . Теперь мы установим между ними связь. Предположим, что план x_ij невырожденный (число базисных клеток в таблице перевозок ровно m + n -1). Для всех этих клеток x_ij >0 . Определим платежи (a _i и b _j ) так, чтобы во всех базисных клетках псевдостоимости были ровны стоимостям:

č _ij = a _i + b _j = с _ij , при x_ij >0.

Что касается свободных клеток (где x_ij = 0), то в них соотношение между псевдостоимостями и стоимостями может быть, какое угодно.

Оказывается соотношение между псевдостоимостями и стоимостями в свободных клетках показывает, является ли план оптимальным или же он может быть улучшен. Существует специальная теорема: Если для всех базисных клеток плана x_ij > 0,

a _i + b _j = č _ij = с _ij ,

а для всех свободных клеток x_ij =0 ,

a _i + b _j = č _ij ≤ с _ij ,

то план является оптимальным и никакими способами улучшен быть не может. Нетрудно показать, что это теорема справедлива также для вырожденного плана, и некоторые из базисных переменных равны нулю. План обладающий свойством :

č _ij = с _ij (для всех базисных клеток ) (1)

č _ij ≤ с _ij ( для всех свободных клеток ) (2)

называется потенциальным планом, а соответствующие ему платежи (a _i и b _j ) — потенциалами пунктов A_i и B_j ( i =1,..., m ; j =1,..., n ). Пользуясь этой терминологией вышеупомянутую теорему можно сформулировать так:

Всякий потенциальный план является оптимальным.

Итак, для решения транспортной задачи нам нужно одно - построить потенциальный план. Оказывается его можно построить методом последовательных приближений, задаваясь сначала какой-то произвольной системой платежей, удовлетворяющей условию (1). При этом в каждой базисной клетке получиться сумма платежей, равная стоимости перевозок в данной клетке; затем, улучшая план следует одновременно менять систему платежей. Так, что они приближаются к потенциалам. При улучшении плана нам помогает следующее свойство платежей и псевдостоимостей: какова бы ни была система платежей (a _i и b _j ) удовлетворяющая условию (1), для каждой свободной клетки цена цикла пересчёта равна разности между стоимостью и псевдостоимостью в данной клетке : g _{i , j} = с _{i , j} - č _{i , j} .

Таким образом, при пользовании методом потенциалов для решения транспортной задачи отпадает наиболее трудоёмкий элемент распределительного метода: поиски циклов с отрицательной ценой.

Процедура построения потенциального (оптимального) плана состоит в следующем.

В качестве первого приближения к оптимальному плану берётся любой допустимый план (например, построенный способом минимальной стоимости по строке). В этом плане m + n - 1 базисных клеток, где m - число строк, n - число столбцов транспортной таблицы. Для этого плана можно определить платежи (a _i и b _j ), так, чтобы в каждой базисной клетке выполнялось условие :

a _i + b _j = с _ij (3)

Уравнений (3) всего m + n - 1 , а число неизвестных равно m + n . Следовательно, одну из этих неизвестных можно задать произвольно (например, равной нулю). После этого из m + n - 1 уравнений (3) можно найти остальные платежи a _i , b _j , а по ним вычислить псевдостоимости, č _{i , j} = a _i + b _j для каждой свободной клетки.

Таблица №5

a ₄ = 0, ®

b ₄ = 6, так как a ₄ + b ₄ = С₄₄ = 6, ®

a ₁ = 0, так как a ₁ + b ₄ = С₁₄ = 6, ®

b ₃ = 5, так как a ₁ + b ₃ = С₁₃ = 5, ®

b ₁ = 7, так как a ₄ + b ₁ = С₄₁ = 7, ®

a ₂ = -1, так как a ₂ + b ₁ = С₂₁ = 6, ®

b ₅ = 6, так как a ₂ + b ₅ = С₂₅ = 5, ®

a ₃ = 1, так как a ₃ + b ₅ = С₃₅ = 7, ®

b ₂ = 6, так как a ₃ + b ₂ = С₂₅ = 7.

Если оказалось, что все эти псевдостоимости не превосходят стоимостей

č _ij £ с _ij , £ ³

то план потенциален и, значит, оптимален. Если же хотя бы в одной свободной клетке псевдостоимость больше стоимости (как в нашем примере), то план не является оптимальным и может быть улучшен переносом перевозок по циклу, соответствующему данной свободной клетке. Цена этого цикла ровна разности между стоимостью и псевдостоимостью в этой свободной клетке.

В таблице № 5 мы получили в двух клетках č _ij ³ с _ij , теперь можно построить цикл в любой из этих двух клеток. Выгоднее всего строить цикл в той клетке, в которой разность č _ij - с _ij максимальна. В нашем случае в обоих клетках разность одинакова (равна 1), поэтому, для построения цикла выберем, например, клетку (4,2):

Таблица №6

Теперь будем перемещать по циклу число 14, так как оно является минимальным из чисел, стоящих в клетках, помеченных знаком - . При перемещении мы будем вычитать 14 из клеток со знаком - и прибавлять к клеткам со знаком + .

После этого необходимо подсчитать потенциалы a _i и b _j и цикл расчетов повторяется.

Итак, мы приходим к следующему алгоритму решения транспортной задачи методом потенциалов.

1. Взять любой опорный план перевозок, в котором отмечены m + n - 1 базисных клеток (остальные клетки свободные).

2. Определить для этого плана платежи (a _i и b _j ) исходя из условия, чтобы в любой базисной клетке псевдостоимости были равны стоимостям. Один из платежей можно назначить произвольно, например, положить равным нулю.

3. Подсчитать псевдостоимости č _{i , j} = a _i + b _j для всех свободных клеток. Если окажется, что все они не превышают стоимостей, то план оптимален.

4. Если хотя бы в одной свободной клетке псевдостоимость превышает стоимость, следует приступить к улучшению плана путём переброски перевозок по циклу, соответствующему любой свободной клетке с отрицательной ценой (для которой псевдостоимость больше стоимости).

5. После этого заново подсчитываются платежи и псевдостоимости, и, если план ещё не оптимален, процедура улучшения продолжается до тех пор, пока не будет найден оптимальный план.

Так в нашем примере после 2 циклов расчетов получим оптимальный план. При этом стоимость всей перевозки изменялась следующим образом: F₀ = 723, F₁ = 709, F₂ = F_min = 703.

Следует отметить так же, что оптимальный план может иметь и другой вид, но его стоимость останется такой же F_min = 703.

Список использованной литературы

1. Еремин И.И., Астафьев Н.Н. Введение в теорию линейного и выпуклого программирования М.; Наука, 1976г.

2. Карманов В.Г. Математическое программирование. – М.; Наука, 1986г.

3. Моисеев Н.Н., Иванов Ю.П., Столярова Е.М. Методы оптимизации. – М.; Наука, 1978г.

4. Иванов Ю.П., Лотов А.В. Математические модели в экономике. – М.; Наука, 1979г.

5. Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М.; Наука, 1986г