Методы прогнозирования финансовых показателей
1.Модель с аддитивной компонентой
Аддитивную модель прогнозирования можно представить в виде формулы:
F = T + S + E
где: F
– прогнозируемое значение; Т
– тренд; S
– сезонная компонента;
Е
– ошибка прогноза.
Алгоритм построения прогнозной модели
Для прогнозирования объема продаж, имеющего сезонный характер, предлагается следующий алгоритм построения прогнозной модели:
1.Определяется тренд,
наилучшим образом аппроксимирующий фактические данные. Существенным моментом при этом является предложение использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели.
2
.Вычитая из фактических значений объёмов продаж значения тренда, определяют
величины сезонной компоненты
и корректируют таким образом, чтобы их сумма была равна нулю.
3.Рассчитываются ошибки модели
как разности между фактическими значениями и значениями модели.
Применение алгоритма рассмотрим на следующем примере.
Исходные данные:
Объемы фактических расходов бюджета _________ района, взяты из месячной и годовой отчетности финансового управления администрации ________ района. Данная статистика характеризуется тем, что значения объёма продаж имеют выраженный сезонный характер с возрастающим трендом. Исходная информация представлена в табл. 1.
табл.1
| Объем фактических расходов
|
| 1 кв. 1999 г.
|
24518
|
| 2 кв. 1999 г.
|
23778
|
| 3 кв. 1999 г.
|
25143
|
| 4 кв. 1999 г.
|
27622
|
| 1 кв. 2000 г.
|
26149
|
| 2 кв. 2000 г.
|
24123
|
| 3 кв. 2000 г.
|
27580
|
| 4 кв. 2000 г.
|
30854
|
| 1 кв. 2001 г.
|
29147
|
| 2 кв. 2001 г.
|
26478
|
| 3 кв. 2001 г.
|
30159
|
| 4 кв. 2001 г.
|
33149
|
| 1 кв. 2002 г.
|
32451
|
Реализуем алгоритм построения прогнозной модели, описанный выше. Решение данной задачи рекомендуется осуществлять в среде MS Excel, что позволит существенно сократить количество расчётов и время построения модели.
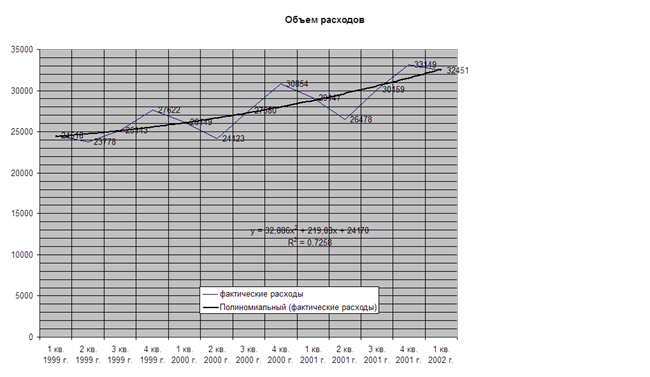 1. Определяем тренд
, наилучшим образом аппроксимирующий фактические данные. Для этого рекомендуется использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели) 1. Определяем тренд
, наилучшим образом аппроксимирующий фактические данные. Для этого рекомендуется использовать полиномиальный тренд, что позволяет сократить ошибку прогнозной модели)
Таблица 2.
Расчёт значений сезонной компоненты
| Значение тренда
|
Сезонная компонента
|
| 1 кв. 1999 г.
|
24518
|
24518
|
0
|
| 2 кв. 1999 г.
|
23778
|
24962
|
-1184
|
| 3 кв. 1999 г.
|
25143
|
25012
|
131
|
| 4 кв. 1999 г.
|
27622
|
25217
|
2405
|
| 1 кв. 2000 г.
|
26149
|
26098
|
51
|
| 2 кв. 2000 г.
|
24123
|
26958
|
-2835
|
| 3 кв. 2000 г.
|
27580
|
27495
|
85
|
| 4 кв. 2000 г.
|
30854
|
28017
|
2837
|
| 1 кв. 2001 г.
|
29147
|
28964
|
183
|
| 2 кв. 2001 г.
|
26478
|
29617
|
-3139
|
| 3 кв. 2001 г.
|
30159
|
30498
|
-339
|
| 4 кв. 2001 г.
|
33149
|
31485
|
1664
|
| 1 кв. 2002 г.
|
32451
|
32451
|
0
|
Скорректируем значения сезонной компоненты таким образом, чтобы их сумма была равна нулю.
Таблица 3.
Расчет средних значений сезонной компоненты
|
| 1999 г.
|
2000 г.
|
2001 г.
|
Итого
|
Среднее
|
Сезонная компонента
|
| 1 кв.
|
0
|
51
|
183
|
234
|
78
|
89,75
|
| 2 кв.
|
-1184
|
-2835
|
-3139
|
-7158
|
-2386
|
-2374,25
|
| 3 кв.
|
131
|
85
|
-339
|
-123
|
-41
|
-29,25
|
| 4 кв.
|
2405
|
2837
|
1664
|
6906
|
2302
|
2313,75
|
| Сумма
|
-47
|
0
|
| -11,75
|
3. Рассчитываем ошибки модели
как разности между фактическими значениями и значениями модели.
Таблица 4.
Расчёт ошибок
| расходы
|
Значение модели
|
Отклонение
|
| 1 кв. 1999 г.
|
24518
|
24607,75
|
-89,75
|
| 2 кв. 1999 г.
|
23778
|
22587,75
|
1190,25
|
| 3 кв. 1999 г.
|
25143
|
24982,75
|
160,25
|
| 4 кв. 1999 г.
|
27622
|
27530,75
|
91,25
|
| 1 кв. 2000 г.
|
26149
|
26187,75
|
-38,75
|
| 2 кв. 2000 г.
|
24123
|
24583,75
|
-460,75
|
| 3 кв. 2000 г.
|
27580
|
27465,75
|
114,25
|
| 4 кв. 2000 г.
|
30854
|
30330,75
|
523,25
|
| 1 кв. 2001 г.
|
29147
|
29053,75
|
93,25
|
| 2 кв. 2001 г.
|
26478
|
27242,75
|
-764,75
|
| 3 кв. 2001 г.
|
30159
|
30468,75
|
-309,75
|
| 4 кв. 2001 г.
|
33149
|
33798,75
|
-649,75
|
| 1 кв. 2002 г.
|
32451
|
32540,75
|
-89,75
|
Находим среднеквадратическую ошибку модели (Е) по формуле:
Е= Σ О2
: Σ (T+S)2
где:
Т
-
трендовое значение объёма расходов;
S
– сезонная компонента;
О
- отклонения модели от фактических значений
Е=(3079106/(361151*361151))*100% = 0,002361%
Величина полученной ошибки позволяет говорить, что построенная модель хорошо аппроксимирует фактические данные, т.е. она вполне отражает экономические тенденции, определяющие объём расходов, и является предпосылкой для построения прогнозов высокого качества.
2. Модель с мультипликативной компонентой.
В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю -фондового значения, т.e. значение сезонной компоненты увеличивается с возрастанием значений тренда. Например, рассмотрим график следующих данных об объемах расходов. Объем продаж этого продукта так же, как и в предыдущем примере, подвержен сезонным колебаниям, и значения его в разные кварталы разные. Однако размах вариации фактических значении относительно линии тренда постоянно возрастает. Такую ситуацию можно представить с помощью модели с мультипликативной компонентой
A=T*S*Е
1.3.1. Расчет сезонной компоненты
Отличие расчета сезонной компоненты для мультипликативной модели от аддитивной модели заключается лишь в том, что в колонку 6 вписываются коэффициенты сезонности (аналог оценок сезонной компоненты в аддитивной модели)
Сезонные коэффициенты
представляют собой доли тренда, поэтому принимают, что их сумма должна равняться количеству сезонов в году, т.е. 4, а не нулю, как в аддитивной модели.
| Итого за 4 квартала
|
Скользящая средняя за 4 квартала
|
Центрированная скользящая средняя
|
Оценка сезонной компоненты
|
| Y
|
S
|
T
|
Y/T=S*E
|
| 1 кв. 1999 г.
|
24518
|
| 2 кв. 1999 г.
|
23778
|
| 3 кв. 1999 г.
|
25143
|
101061
|
25265,25
|
| 4 кв. 1999 г.
|
27622
|
102692
|
25673
|
25469,125
|
1,084528817
|
| 1 кв. 2000 г.
|
26149
|
103037
|
25759,25
|
25716,125
|
1,016832824
|
| 2 кв. 2000 г.
|
24123
|
105474
|
26368,5
|
26063,875
|
0,925533905
|
| 3 кв. 2000 г.
|
27580
|
108706
|
27176,5
|
26772,5
|
1,030161546
|
| 4 кв. 2000 г.
|
30854
|
111704
|
27926
|
27551,25
|
1,119876594
|
| 1 кв. 2001 г.
|
29147
|
114059
|
28514,75
|
28220,375
|
1,032835318
|
| 2 кв. 2001 г.
|
26478
|
116638
|
29159,5
|
28837,125
|
0,918191394
|
| 3 кв. 2001 г.
|
30159
|
118933
|
29733,25
|
29446,375
|
1,024200772
|
| 4 кв. 2001 г.
|
33149
|
122237
|
30559,25
|
30146,25
|
1,099606087
|
| 1 кв. 2002 г.
|
32451
|

Десезонализация данных при расчете тренда
Десезонализация данных производится по формуле:
 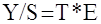
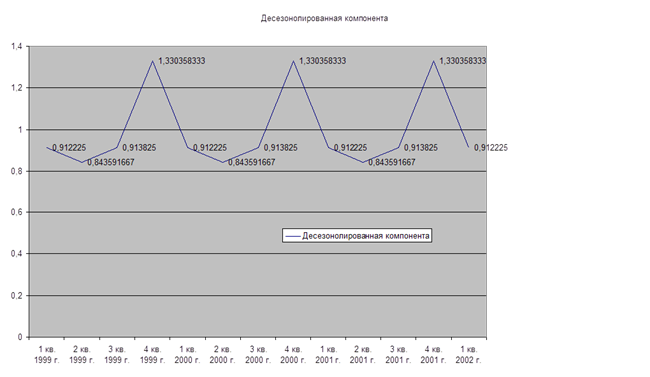
 Точки, образующие представленный на графике тренд, достаточно сильно разбросаны, что более близко к реальной действительности, чем в предыдущем примере.
Точки, образующие представленный на графике тренд, достаточно сильно разбросаны, что более близко к реальной действительности, чем в предыдущем примере.
| 1999 г.
|
2000 г.
|
2001 г.
|
Итого
|
Среднее
|
Сезонная компонента
|
| 1 кв.
|
1,0168
|
1,0328
|
2,0496
|
0,6832
|
0,912225
|
| 2 кв.
|
0,9255
|
0,9182
|
1,8437
|
0,6146
|
0,843592
|
| 3 кв.
|
1,0302
|
1,0242
|
2,0544
|
0,6848
|
0,913825
|
| 4 кв.
|
1,0845
|
1,1199
|
1,0996
|
3,304
|
1,1013
|
1,330358
|
| Сумма
|
3,0839
|
4
|
| 0,9161
|
0,229
|
| Фактический объем расходов
|
Сезонная компонента
|
Десезонолизированный объем продаж
|
| Y
|
S
|
Y/S
|
| 1 кв. 1999 г.
|
24518
|
0,912225
|
26877,14106
|
| 2 кв. 1999 г.
|
23778
|
0,843591667
|
28186,62267
|
| 3 кв. 1999 г.
|
25143
|
0,913825
|
27514,02074
|
| 4 кв. 1999 г.
|
27622
|
1,330358333
|
20762,82706
|
| 1 кв. 2000 г.
|
26149
|
0,912225
|
28665,07715
|
| 2 кв. 2000 г.
|
24123
|
0,843591667
|
28595,58831
|
| 3 кв. 2000 г.
|
27580
|
0,913825
|
30180,83331
|
| 4 кв. 2000 г.
|
30854
|
1,330358333
|
23192,2477
|
| 1 кв. 2001 г.
|
29147
|
0,912225
|
31951,54704
|
| 2 кв. 2001 г.
|
26478
|
0,843591667
|
31387,22328
|
| 3 кв. 2001 г.
|
30159
|
0,913825
|
33003,03669
|
| 4 кв. 2001 г.
|
33149
|
1,330358333
|
24917,34683
|
| 1 кв. 2002 г.
|
32451
|
0,912225
|
35573,46049
|
Расчет ошибок
Ошибки прогнозируемых объемов расходов расчитывают по формуле:
E =A/(T*S)
| Объем расходов
|
Сезонная компонента
|
Тренд
|
Ошибка
|
| 1 кв. 1999 г.
|
24518
|
0,912225
|
26877,1411
|
1
|
| 2 кв. 1999 г.
|
23778
|
0,84359167
|
28186,6227
|
1
|
| 3 кв. 1999 г.
|
25143
|
0,913825
|
27514,0207
|
1
|
| 4 кв. 1999 г.
|
27622
|
1,33035833
|
20762,8271
|
1
|
| 1 кв. 2000 г.
|
26149
|
0,912225
|
28665,0771
|
1
|
| 2 кв. 2000 г.
|
24123
|
0,84359167
|
28595,5883
|
1
|
| 3 кв. 2000 г.
|
27580
|
0,913825
|
30180,8333
|
1
|
| 4 кв. 2000 г.
|
30854
|
1,33035833
|
23192,2477
|
1
|
| 1 кв. 2001 г.
|
29147
|
0,912225
|
31951,547
|
1
|
| 2 кв. 2001 г.
|
26478
|
0,84359167
|
31387,2233
|
1
|
| 3 кв. 2001 г.
|
30159
|
0,913825
|
33003,0367
|
1
|
| 4 кв. 2001 г.
|
33149
|
1,33035833
|
24917,3468
|
1
|
| 1 кв. 2002 г.
|
32451
|
0,912225
|
35573,4605
|
1
|
Можно предположить, что величина ошибки второго прогноза будет несколько ниже чем первого.
3. Прогноз методом скользящей средней и экспоненциального сглаживания.
Для предсказаний значений временного ряда можно использовать более простую методику.
При расчете скользящей средней Yt
np
c
(m) все m значений параметра Y за m моментов времени учитываются с одинаковым весовым коэффициентом 1/m что не всегда обосновано. Для прогнозирования технико – экономических трендов момент времени, в котором наблюдалось значение параметра Y, играет решающее значение. Естественно предположить, что зависимость во временных рядах постепенно ослабевает с увеличением периода между двумя соседними точками. Так, если зависимость прогнозируемою параметра Yt
представляется более сильной от значения Yt-1
, чем от Yt-s
то
наблюдениям временного ряда следует придавать веса, которые должны уменьшаться но мере удаления oт фиксированного момента времени t. Это обстоятельство учитывается в методе экспоненциального сглаживания. Таким образом, при вычислении .ко экспоненциальной средней используются лишь предшествующая экспоненциальная средняя и последнее наблюдение, а все предыдущие наблюдения игнорируются.
Например, пусть необходимо дать прогноз для t-=8 но данным следующего временного ряда: 1) методом скользящей средней для m=3, m =4$ 2) методом экспоненциального о сглаживания для 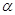 =0,2; 0,6. =0,2; 0,6.
| 1 кв. 1999 г.
|
24518
|
| 2 кв. 1999 г.
|
23778
|
| 3 кв. 1999 г.
|
25143
|
| 4 кв. 1999 г.
|
27622
|
| 1 кв. 2000 г.
|
26149
|
| 2 кв. 2000 г.
|
24123
|
| 3 кв. 2000 г.
|
27580
|
| 4 кв. 2000 г.
|
30854
|
| 1 кв. 2001 г.
|
29147
|
| 2 кв. 2001 г.
|
26478
|
| 3 кв. 2001 г.
|
30159
|
| 4 кв. 2001 г.
|
33149
|
| 1 кв. 2002 г.
|
32451
|
Метод скользящей средней
Y14
пр
с
(3) = (30159+33149+32451)/3=31919,67
Y14
пр с
(13) = (24518+23778+25143+27622+26149+24123+27580+30854+29147+ 26478+30159+33149+32451)/13 = 27780,846
Метод экспоненциального сглаживания
| 0,2
|
погрешность
|
| 1 кв. 1999 г.
|
24518
|
#Н/Д
|
#Н/Д
|
| 2 кв. 1999 г.
|
23778
|
23778
|
#Н/Д
|
| 3 кв. 1999 г.
|
25143
|
24870
|
#Н/Д
|
| 4 кв. 1999 г.
|
27622
|
27071,6
|
#Н/Д
|
| 1 кв. 2000 г.
|
26149
|
26333,52
|
1851,838704
|
| 2 кв. 2000 г.
|
24123
|
24565,1
|
2106,426154
|
| 3 кв. 2000 г.
|
27580
|
26977,02
|
2223,149967
|
| 4 кв. 2000 г.
|
30854
|
30078,6
|
3109,499653
|
| 1 кв. 2001 г.
|
29147
|
29333,32
|
2886,08454
|
| 2 кв. 2001 г.
|
26478
|
27049,06
|
2831,47259
|
| 3 кв. 2001 г.
|
30159
|
29537,01
|
2496,160001
|
| 4 кв. 2001 г.
|
33149
|
32426,6
|
3207,855423
|
| 1 кв. 2002 г.
|
32451
|

| 0,6
|
погрешность
|
| 1 кв. 1999 г.
|
24518
|
#Н/Д
|
#Н/Д
|
| 2 кв. 1999 г.
|
23778
|
23778
|
#Н/Д
|
| 3 кв. 1999 г.
|
25143
|
24324
|
#Н/Д
|
| 4 кв. 1999 г.
|
27622
|
25643,2
|
#Н/Д
|
| 1 кв. 2000 г.
|
26149
|
25845,52
|
2081,334719
|
| 2 кв. 2000 г.
|
24123
|
25156,51
|
2167,926259
|
| 3 кв. 2000 г.
|
27580
|
26125,91
|
1741,283327
|
| 4 кв. 2000 г.
|
30854
|
28017,14
|
3224,65661
|
| 1 кв. 2001 г.
|
29147
|
28469,09
|
3136,065979
|
| 2 кв. 2001 г.
|
26478
|
27672,65
|
3032,922749
|
| 3 кв. 2001 г.
|
30159
|
28667,19
|
1951,31804
|
| 4 кв. 2001 г.
|
33149
|
30459,91
|
3174,532132
|
| 1 кв. 2002 г.
|
32451
|

рис. 8.
Число членов скользящей средней m и параметр -экспоненциального сглаживания (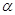 определяется статистикой исследуемою процесса. Чем мень-ше m и чем больше определяется статистикой исследуемою процесса. Чем мень-ше m и чем больше 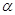 , тем сильнее peaгирует пpoгноз на колебания временного ряда, и наоборот, чем больше m и чем меньше , тем сильнее peaгирует пpoгноз на колебания временного ряда, и наоборот, чем больше m и чем меньше 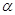 , чем более инерционным является процесс прогнозирования. Для подбора оптимального параметра прогнозирования необходимо провести сглаживание временною ряда с помощью нескольких различных значений параметра m или , чем более инерционным является процесс прогнозирования. Для подбора оптимального параметра прогнозирования необходимо провести сглаживание временною ряда с помощью нескольких различных значений параметра m или 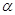 затем определить среднюю ошибку прогнозов и выбрать параметр, соответствующий минимальной ошибке. затем определить среднюю ошибку прогнозов и выбрать параметр, соответствующий минимальной ошибке.
|