- Задание.
Решить
прямую задачу
размерной цепи
механизма
толкателя,
изображённого
на рисунке
1.1., методами
максимума-минимума
и вероятностным.
Способ решения
стандартный,
А3
= 100 мм

Рис
1.1.
А2
А1
     
               
 
      
   
                  
А     3 3
    
  
              
          
 

                 
     А3
А3

А4
А5
А
   
 (
Схема механизма
толкателя )
(
Схема механизма
толкателя )
Обозначения:
А1 –
длина поршня;
А2
– радиус поршня;
А3
– расстояние
между осями
отверстий в
толкателе;
А4
– расстояние
от торца крышки
до оси отверстия
в ней;
А5
– длина корпуса;
А - вылет
поршня за пределы
корпуса;
- вылет
поршня за пределы
корпуса;
Таблица
1.1. ( исходные
данные )
|
А1,
мм
|
А2,мм
|
А3,мм
|
А4,мм
|
А5,мм
|
А ,мм ,мм
|
 ,град ,град
|
%,риска |
|
   175
175
|
20 |
100
|
110
|
153 |
А +0,45 +0,45
|
420
|
1,0 |
Аi
– номинальные
размеры составляющих
звеньев,
А - предельное
отклонение
размера
- предельное
отклонение
размера
( А’3
= А3
Сos )
)
Таблица
1.2.
|
  Закон
распределения
действительных
размеров Закон
распределения
действительных
размеров
|
|
|
|
|
Коэффициент
относительного
рас-сеивания
взятый в квадрате
(
 ’i
)2 ’i
)2
|

|

|

|
- Краткая
теория.
- Основные
определения.
Размерная
цепь –
совокупность
размеров,
образующих
замкнутый
контур и непосредственно
участвующих
в решении
поставленной
задачи. Размерные
цепи бывают
плоские, параллельные
и пространственные.
Замкнутость
– является
обязательным
условием размерной
цепи.
- Размерные
цепи состоят
из звеньев:

ЗВЕНЬЯ
 
 
СОСТАВЛЯЮЩИЕ
ЗАМЫКАЮЩИЕ
Аi,
Вi
ИСХОДНЫЕ
  Ai
,
BI
Ai
,
BI
 
УВЕЛИЧИВАЮЩИЕ
УМЕНЬШАЮЩИЕ
Замыкающий
размер ( звено
) – размер
( звено ), которое
получается
при обработке
деталей или
при сборке
узла последним.
Увеличивающий
размер ( звено
) – размер
( звено ), при
увеличении
которого
замыкающий
размер увеличивается.
Для плоских
параллельных
размерных цепей
 =
+1 =
+1
 Где: Где:
 =
=
 - коэффициент
влияния.
- коэффициент
влияния.
Уменьшающий
размер
– размер, при
увеличении
которого
замыкающий
размер уменьшается.
 = -1
= -1
- Задачи
размерных
цепей.
Существует
две задачи для
размерных
цепей: прямая
и обратная.
Обратная
задача
заключается
в определении
номинального
размера, координат
середины поля
допуска и
предельных
отклонений
замыкающего
звена при заданных
аналогичных
значениях
составляющих
звеньев.
(
синтез ) заключается
в заключении
номинальных
размеров,
координат
середин полей
допусков, допусков
и предельных
отклонений
составляющих
звеньев по
заданным
аналогичным
значениям
исходного
звена.
Прямая задача
не решается
однозначно.
2.2.1.1.
Основные
закономерности
размерных
цепей.
Связь
номинальных
размеров.
А =
=

Где:
А - номинальный
размер исходного
звена;
- номинальный
размер исходного
звена;
А - номинальный
размер составляющих
звеньев;
- номинальный
размер составляющих
звеньев;
 i
- коэффициент
влияния; i
- коэффициент
влияния;
n-1 – количество
составляющих
звеньев.
Связь
координат
середин полей
допусков:

=
= i i
 0i
, где 0i
, где
 0i
- координата
середины поля
допуска i-го
составляющего 0i
- координата
середины поля
допуска i-го
составляющего
звена

- координата
середины поля
допуска замыкающего
звена.
- координата
середины поля
допуска замыкающего
звена.
Связь
допусков.
Метод
максимума-минимума.
Т =
=
 Тi Тi
- Метод
теоретико-вероятностный.
Т = t
= t  , где
, где
t
- коэффициент
риска, который
выбирают с
учетом заданного
процента
риска р.
 - коэффициент
относительного
рассеяния.
- коэффициент
относительного
рассеяния.
- Связь
предельных
размеров звеньев.
 =
=
 +
+

Способы
решения прямой
задачи.
- Способ
равных допусков.
Его
принимают, если
несколько
составляющих
звеньев имеют
один порядок
и могут быть
выполнены с
примерно одинаковой
точностью, т.е.
:
Т1
= Т2
= Т3
= … = Тn-1
Для метода
max/min : Ti
=

Для т/в
метода:
Тi
=

Расчетное
значение допусков
округляют до
стандартных
по ГОСТ 6639-69, при
этом выбирают
стандартные
поля допусков
предпочтительного
применения.
Если для
метода max/min
равенство не
точно, а для
Т/В метода не
выполняется
неравенство
Т
 t
t  в пределах
10%, то один из
допусков
корректируют.
в пределах
10%, то один из
допусков
корректируют.
Способ
равных допусков
прост, но на
него накладываются
ограничения:
номинальные
размеры должны
быть близки
и технология
обработки
деталей должна
быть примерно
одинакова.
Способ
одного квалитета.
Этот
способ применяют,
если все составляющие
цепь размеры
могут быть
выполнены с
допуском одного
квалитета и
допуски составляющих
размеров зависят
от их номинального
значения.
Для
теоретико-вероятностного
метода:
T
=
 = aср.
= aср.
По условию
задачи
a 1
= a 2
= … =a n-1
= aср
, где ai
- число единиц
допуска, содержащееся
в допуске данного
i-го размера:
aср
=
 
Для метода
min/max:
T
= aср , aср
, aср
 = =

При невыполнении
этих условий
один из допусков
корректируется
по другому
квалитету.
Ограничение
способа -–сложность
изготовления
должна быть
примерно одинакова.
- Стандартный
способ ГОСТ
16320 – 80
Для
метода
max/min:
Тср =

Для
т/в метода:
Тср
=

С
учётом величины
номинальных
размеров и
сложности их
изготовления
и ориентируясь
на Тср
назначаются
допуски на все
составляющие
звенья по ГОСТ
6656 – 69.
При необходимости
один из допусков
корректируется.
Этот способ
не имеет ограничений,
но у него существует
недостаток:
он субъективный
( не подлежит
автоматизации)
Обоснование
выбора способа
решения.
Так как
сложность
изготовления
деталей нашего
механизма
разные и технология
изготовления
и обработки
тоже разная,
а так же номинальные
размеры деталей
отличаются
на порядок ( А1
и А2
), то мы не можем
применить
способ равных
допусков и
способ одного
квалитета. Мы
буде применять
стандартный
способ.
2.5.
Методы решения
размерных
цепей.
Метод
максимума -
минимума ( max
/ min )
В этом методе
допуск замыкающего
размера определяется
арифметическим
сложением
допусков составляющих
размеров.
Т =
=

Метод учитывает
только предельные
отклонения
звеньев размеров
цепи и самые
неблагоприятные
их сочетания,
обеспечивает
заданную точность
сборки бес
подгонки деталей
– полную
взаимозаменяемость.
Этот метод
экономически
целесообразен
лишь для машин
невысокой
точности или
для цепей, состоящих
из малого числа
звеньев.
Теоретико-вероятностный
метод ( Т /
В )
При допуске
ничтожно малой
вероятности
несоблюдения
предельных
значений замыкающего
размера, значительно
расширяются
допуски составляющих
размеров и тем
самым снижается
себестоимость
изготовления
деталей.
T = t
= t 
Где:
t - коэффициент
риска, который
выбирается
с учётом
- коэффициент
риска, который
выбирается
с учётом
заданного
процента риска
p.
 i’
– коэффициент
относительного
рассеивания. i’
– коэффициент
относительного
рассеивания.
Практическая
часть.
Определение
номинальных
размеров замыкающих
звеньев.
A
=
 (2.3.1)
(2.3.1)
Определим,
какие звенья
увеличивающие,
какие уменьшающие.
Для этого построим
схему размерной
цепи.
     А2
А1
Рис.3.1 Схема
размерной цепи.
А2
А1
Рис.3.1 Схема
размерной цепи.
Приведем
схему размерной
цепи
А3
к плоской
параллельной
схеме.
А4
А
  
  
А  3
А2
А1 3
А2
А1 
   Рис.3.2Схема
плоской параллельной
Рис.3.2Схема
плоской параллельной
размерной
цепи.
А3=
А3*Cos
= 100 *
Cos42
= 74.3мм.
А     4
А5
А 4
А5
А
Из рис.
3.2 следует, что
:
А1,
А2,
А3
-увеличивающие;
А4,
А5
- уменьшающие
размеры.
Следовательно:
1
2
3
1 , а
4
= 5
= -1
Подставляем
в формулу 2.3.1
А
= А1
+ А2
+ А3’
- А4
- А5
= 175 + 20 + 74,3 – 110 – 153 = 6,3 мм.
А
0 вылет поршня.
0 вылет поршня.
Назначение
допусков.
 = +0,12
= +0,12  = 0
= 0
Т
=  -
-  = +0,12 + 0 = 0,12
= +0,12 + 0 = 0,12
Метод
максимума –
минимума.
Рассчитываем
средний допуск.
 =
=
 =
=
 = 0,024
= 0,024
Ориентируемся
на средний
допуск с учетом
сложности
изготовления
детали и величины
ее номинального
размера.
Таблица
3.2.1.2.
| Сложность
изготовления |
Номинальный
размер |

|
|
Max
A
A
A
A
Min
A
|
A
A
A
A
A
|
A
A = A
= A
A
A
|
Максимальный
допуск назначаем
на размер A .
Несколько
меньший допуск
назначаем на
A .
Несколько
меньший допуск
назначаем на
A и A
и A .
Номинальный
допуск назначаем
на размер A .
Номинальный
допуск назначаем
на размер A .
Мы назначаем
max допуск
на размер A .
Мы назначаем
max допуск
на размер A ,
т.к. этот размер
является межосевым
расстоянием
между двумя
отверстиями
сложной формы.
Для назначения
допусков на
размеры используем
ГОСТ 6636-69 разд.
Ra10: ,
т.к. этот размер
является межосевым
расстоянием
между двумя
отверстиями
сложной формы.
Для назначения
допусков на
размеры используем
ГОСТ 6636-69 разд.
Ra10:
Т = 0,05 мм.
= 0,05 мм.
T4
= Т5
= 0,025 мм.
Т2
= Т1
= 0,01 мм.
Проверяем
правильность
назначения
допусков.
Т
=
 = 0,05 + 0,025 + 0,025 + 0,01 + 0,01 = 0,12 мм.
= 0,05 + 0,025 + 0,025 + 0,01 + 0,01 = 0,12 мм.
Допуски
назначены
верно.
Теоретико-вероятностный
метод.
 Т
Т
 t
t  не
более 10%
не
более 10%
Рассчитываем
средний допуск.
Тср
=
 =
=
 =
=
 =0,0454
мм
=0,0454
мм
t = 2,57 для р = 1%
= 2,57 для р = 1%
Ориентируемся
на средний
допуск с учетом
сложности
изготовления
детали и ее
номинального
размера. Для
назначения
допусков
используем
ГОСТ 6636-69 ряд Rа20:
Т = 0,1 ,
T4
=
T5
=0,04, T1
= 0,02, T2
= 0,01
= 0,1 ,
T4
=
T5
=0,04, T1
= 0,02, T2
= 0,01
T
 t
t  =
=
=2,57
 = =
=2,57
 =
=
=2,57
 = 0,1119
= 0,1119
 0,12 >
0,1119 на
6,75%
0,12 >
0,1119 на
6,75%
 Допуски
назначены
верно.
Допуски
назначены
верно.
Назначение
координат
середин полей
допусков
составляющих
звеньев.
 =
=
  ,
где ,
где
 - назначается
произвольно
из конструктивных
соображений.
После расчета
предельные
отклонения
не должны иметь
четвертого
знака после
запятой.
- назначается
произвольно
из конструктивных
соображений.
После расчета
предельные
отклонения
не должны иметь
четвертого
знака после
запятой.
 =
=
 мм
мм
Чаще
всего для наружных
размеров
 = -
= -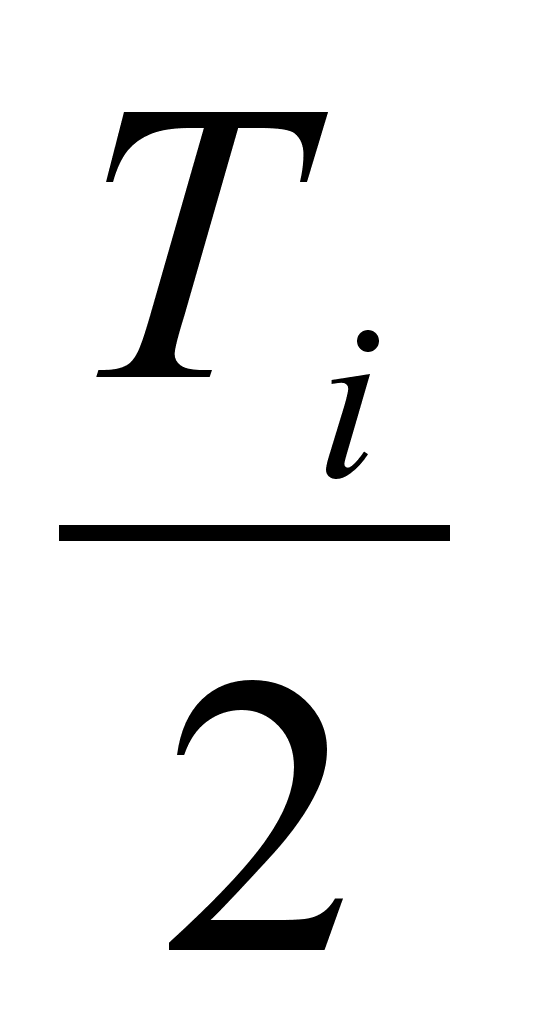
для
внутренних
размеров
 =
=
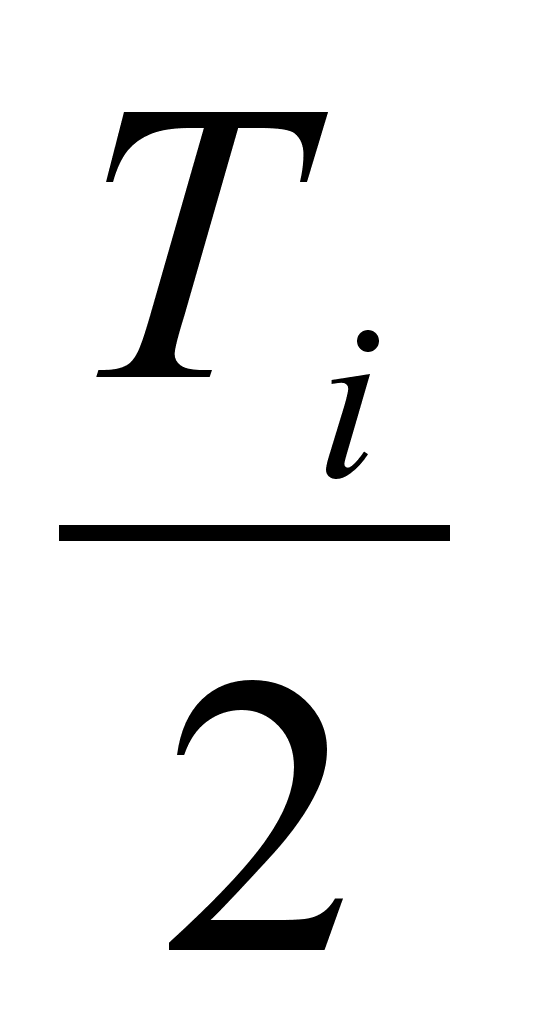
Для метода
max/min
 мм
мм
 мм
мм
 мм
мм
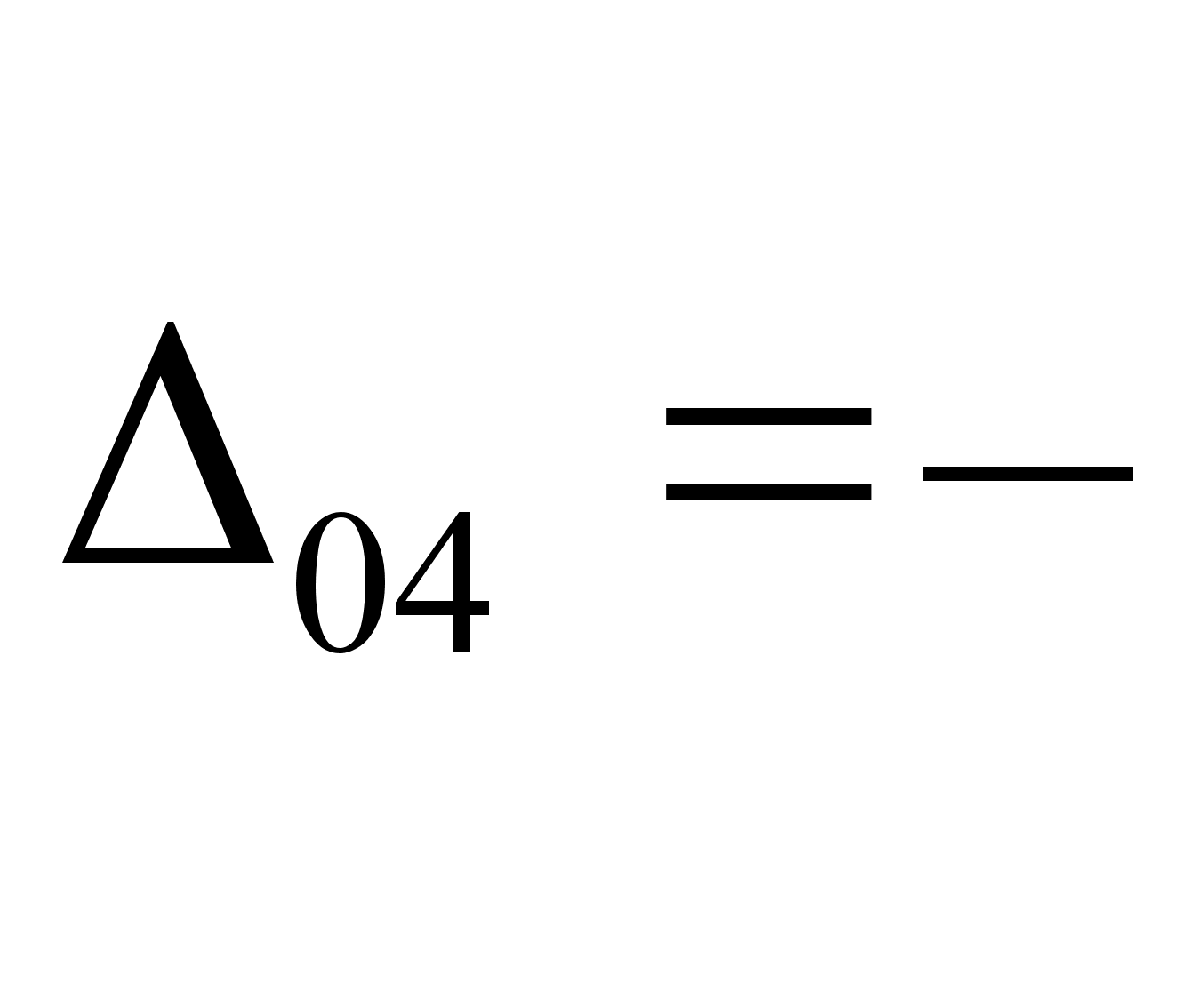  мм
мм
 мм
мм
Проверка
 = 0,005+0,005+0,025+0,0125+0,0125=
= 0,005+0,005+0,025+0,0125+0,0125=
= 0,01+0,025+0,025 = +0,06
Для
теоретико-вероятностного
метода
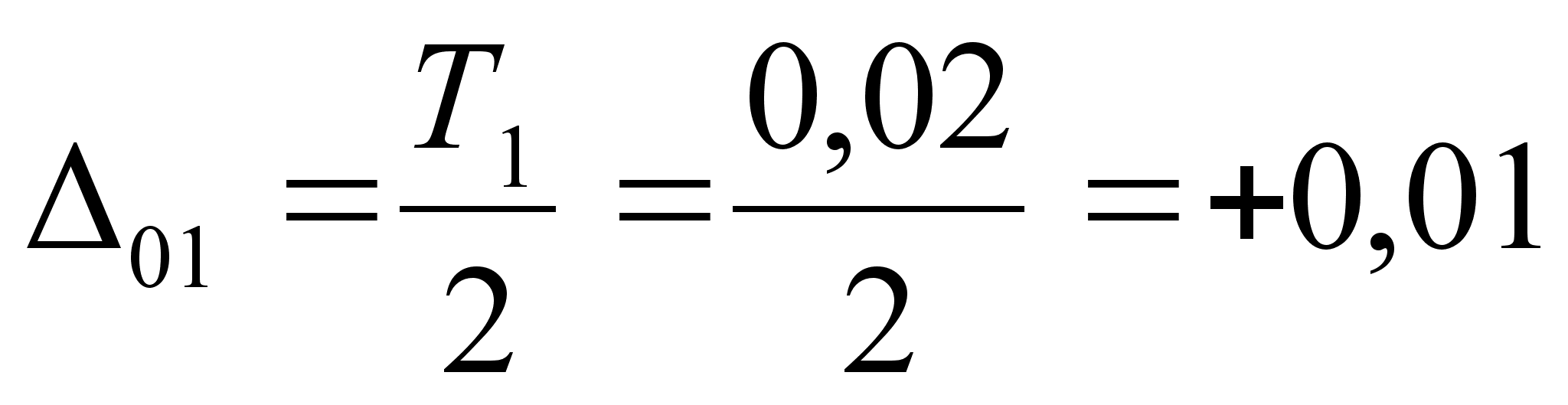 мм
мм
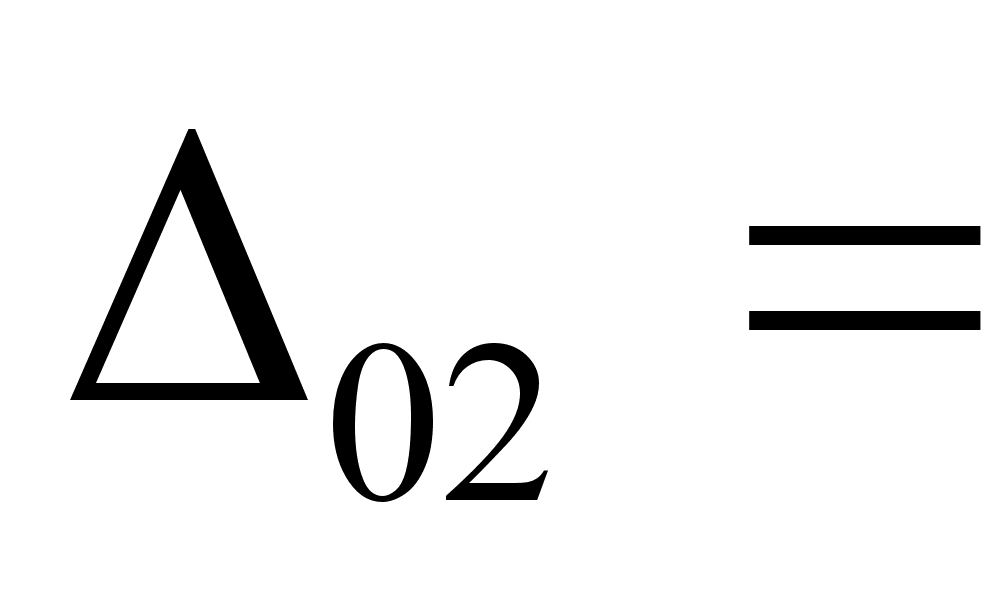 0
0
 мм
мм
 мм
мм
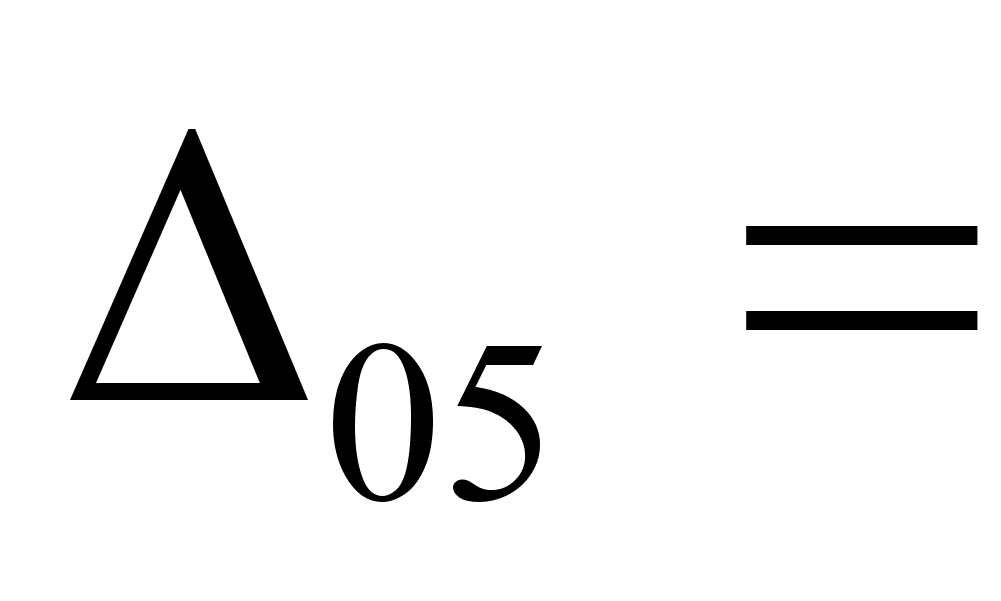 - - мм
мм
Проверка
 = 0,01 +
0,05 + 0,02(-1) - 0,02(-1) = +0,06
= 0,01 +
0,05 + 0,02(-1) - 0,02(-1) = +0,06
Определение
верхних и нижних
отклонений
 ; ;

Для метода
максимума-минимума
 0,005 +
0,005 +
 +0,01 мм
+0,01 мм
 0,005 +
0,005 + = +0,01 мм
= +0,01 мм
 0,025 +
0,025 + = +0,05 мм
= +0,05 мм
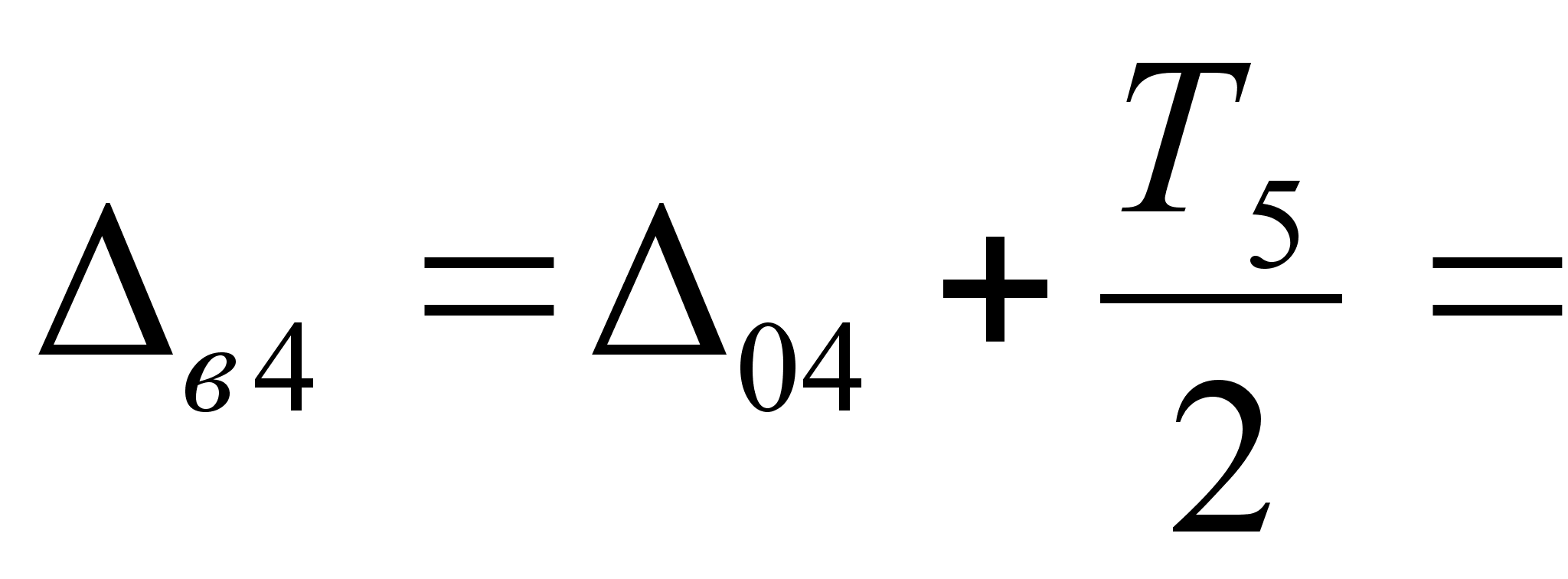 -0,0125 +
-0,0125 +
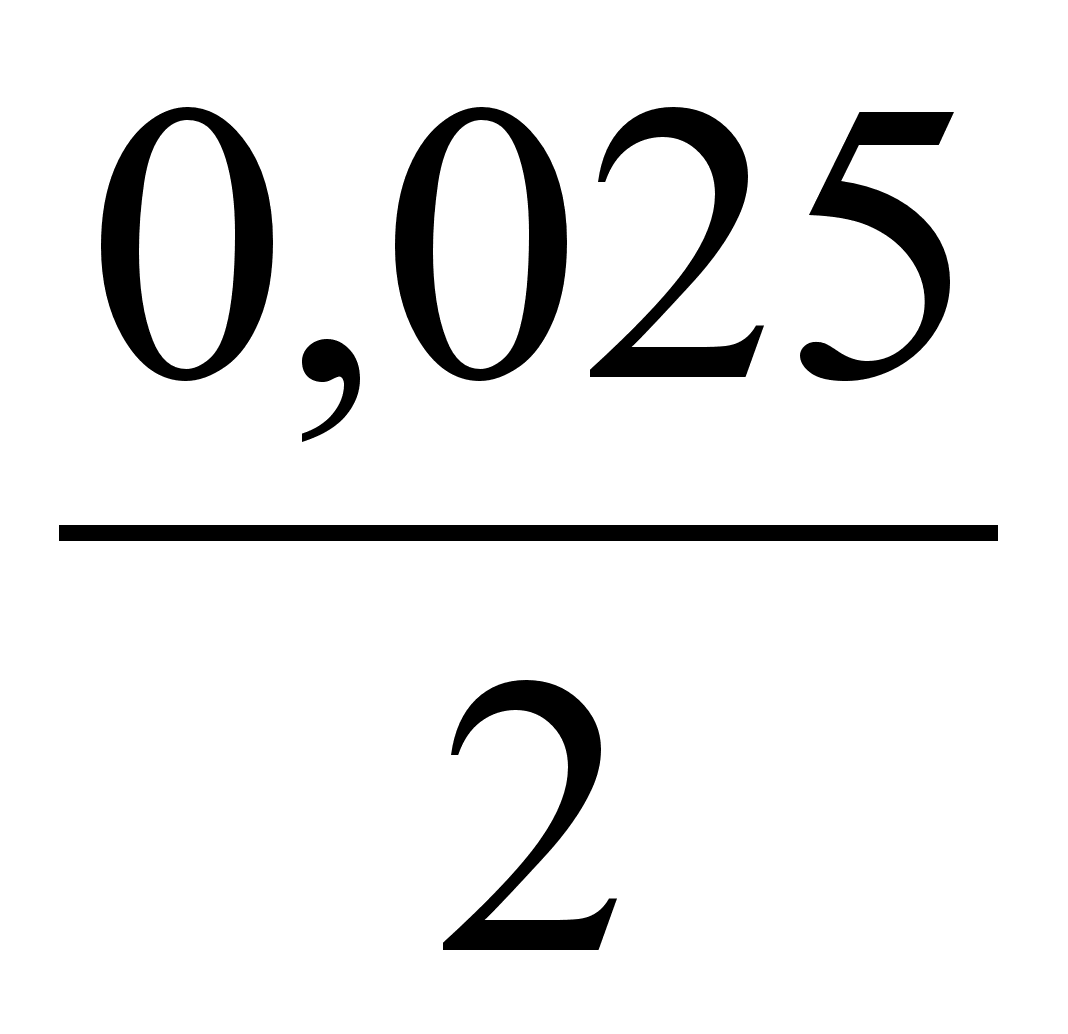 = 0
= 0
 -0,0125 +
-0,0125 +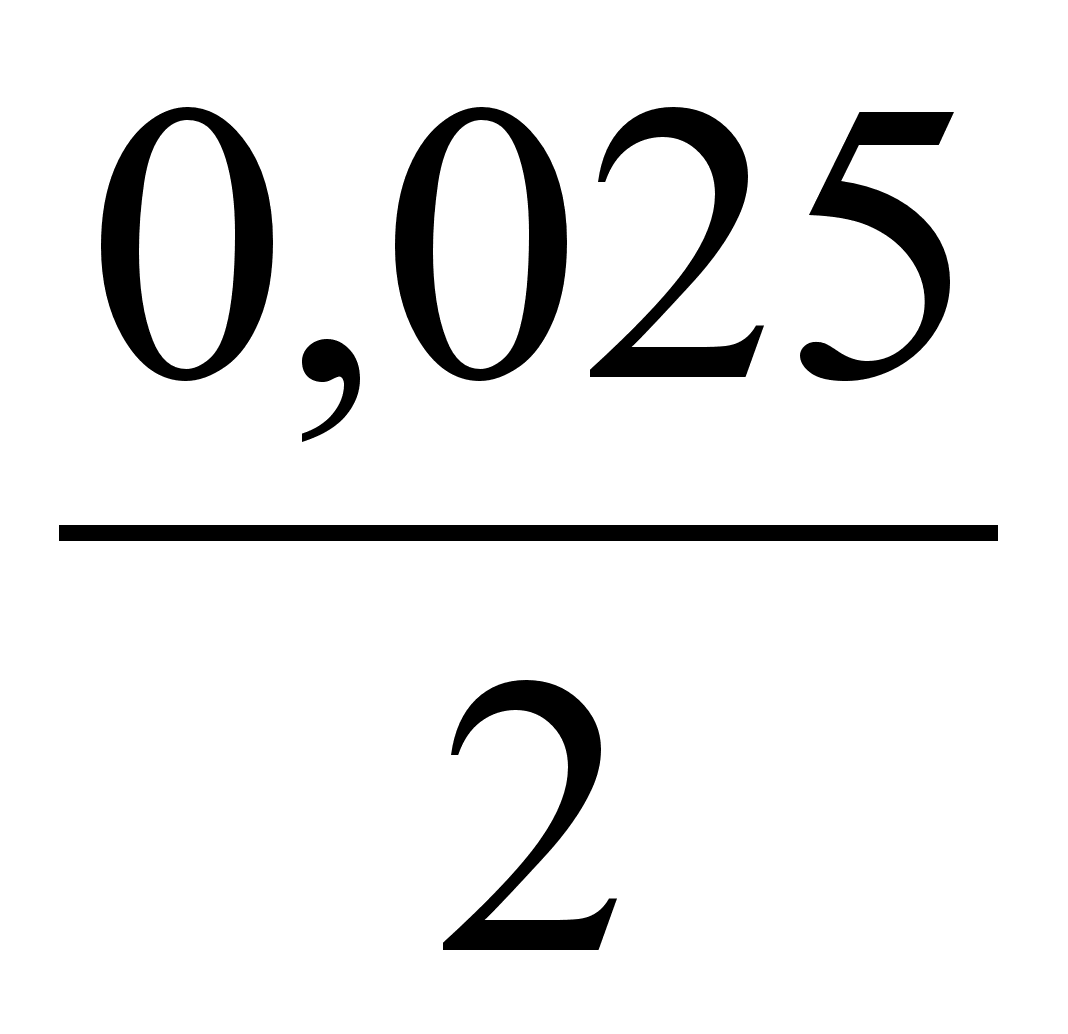 = 0
= 0
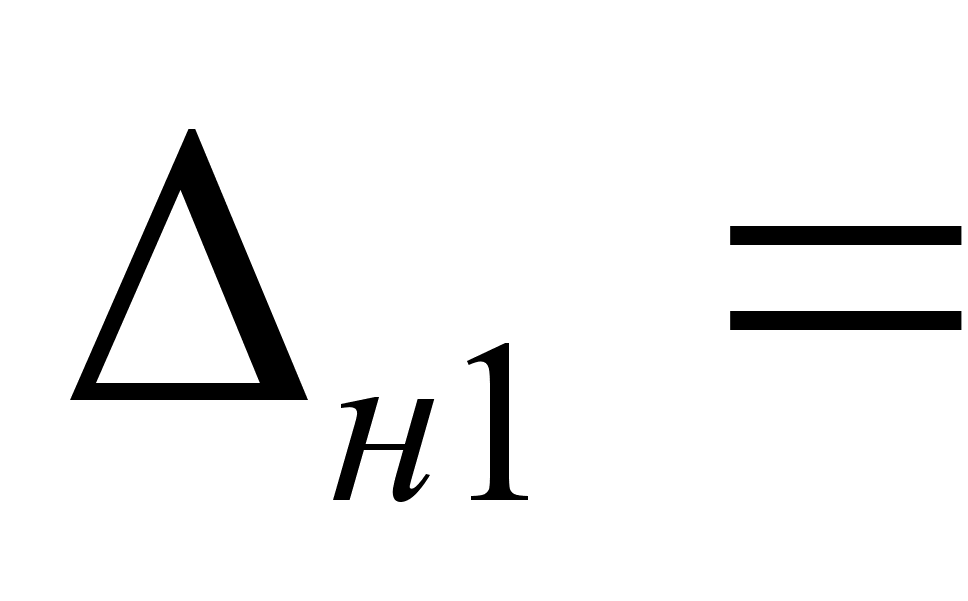  = -0,0125 +
= -0,0125 +
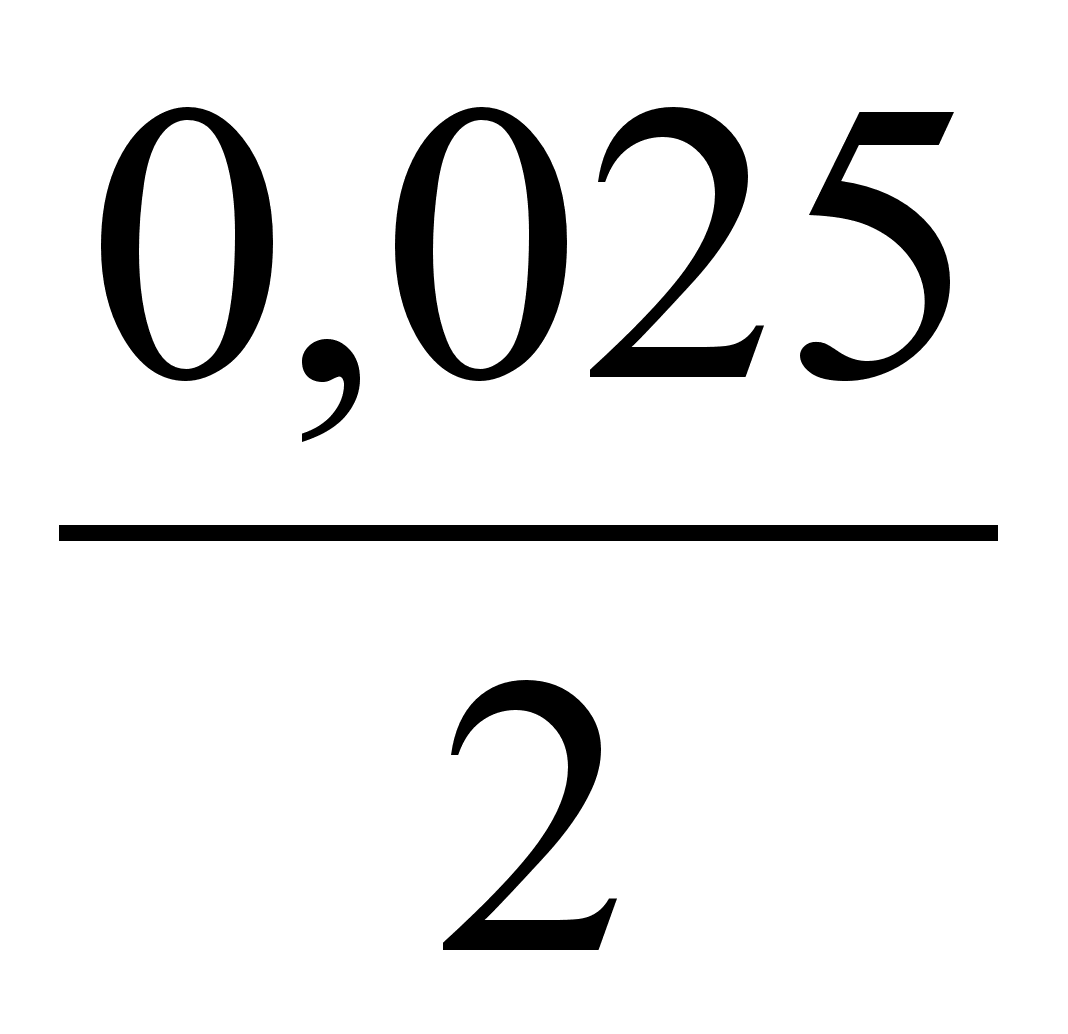 = 0
= 0
 0
0
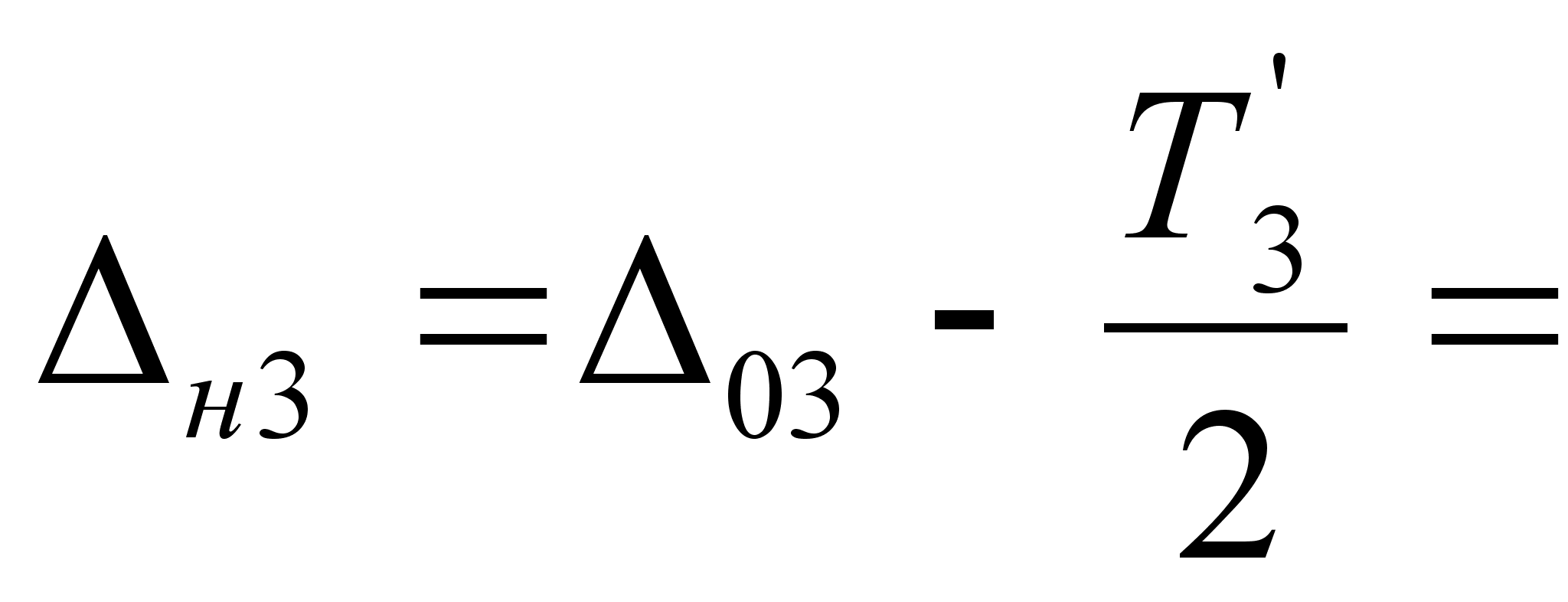 0,025
- 0,025
-
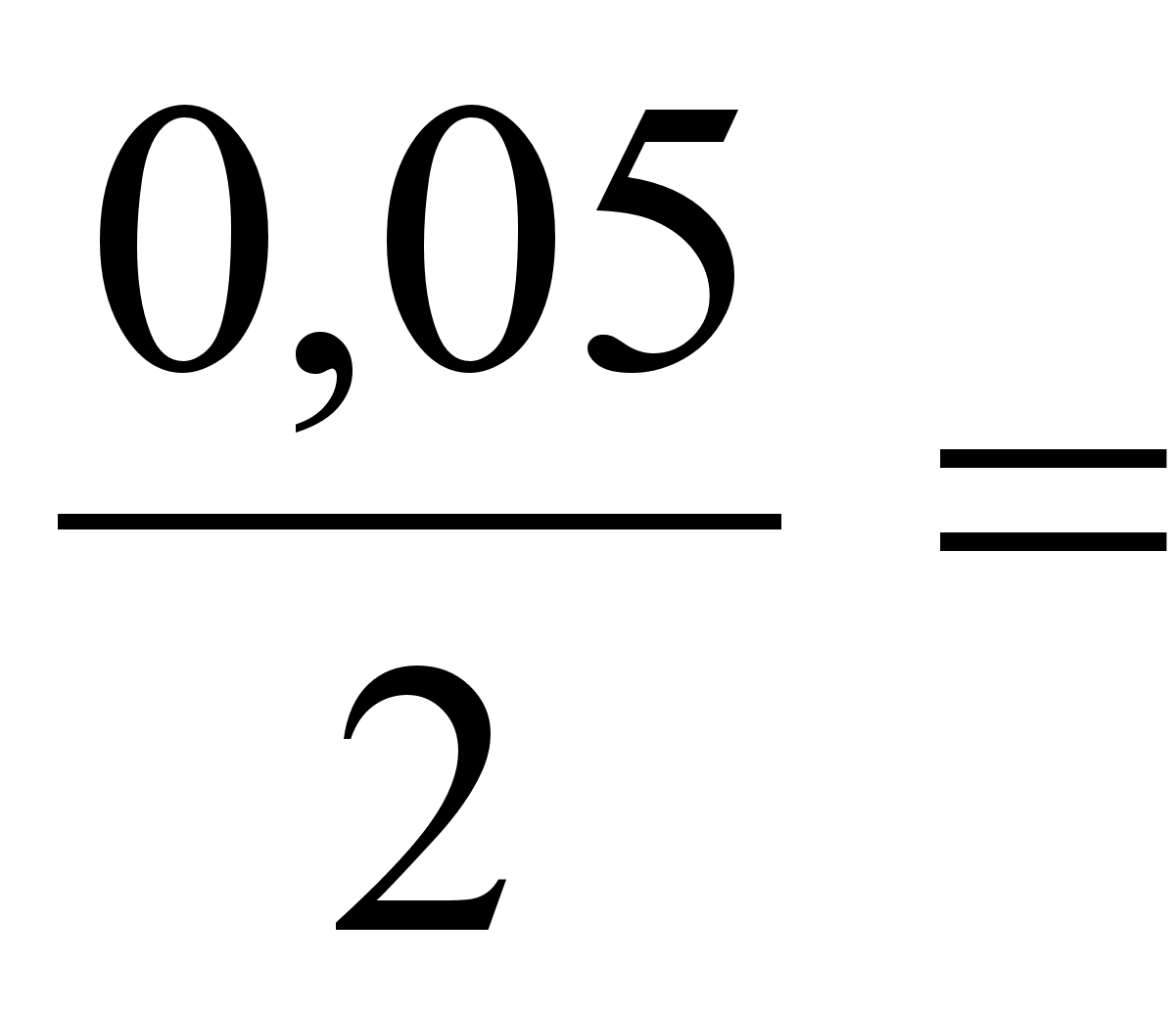 0
0
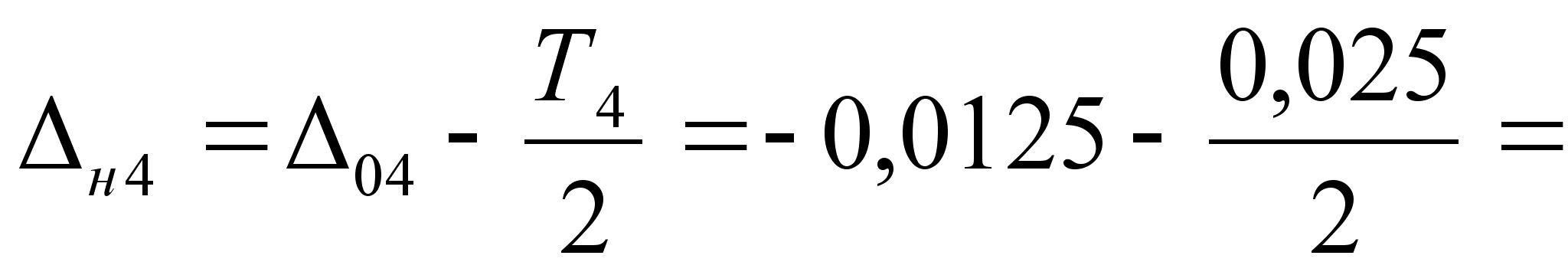 -0,025 мм
-0,025 мм
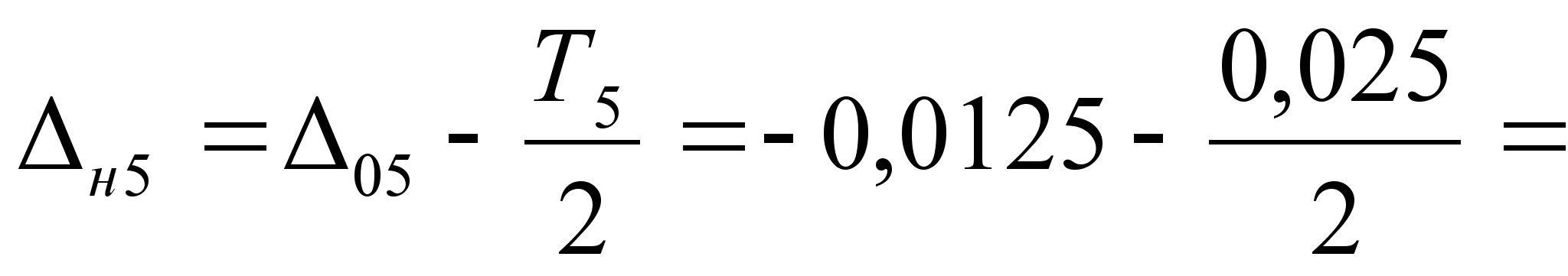 -0,025 мм
-0,025 мм
Для
теоретико-вероятностного
метода
 = 0,01+
= 0,01+ +0,02 мм
+0,02 мм
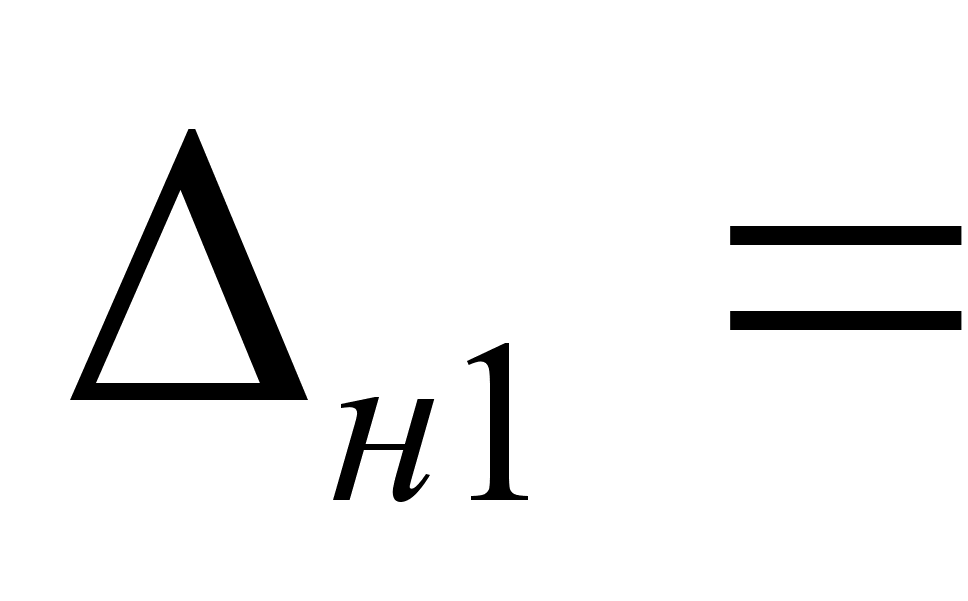 0,01-
0,01- 0
0
 0 +
0 +
 +0,005 мм
+0,005 мм
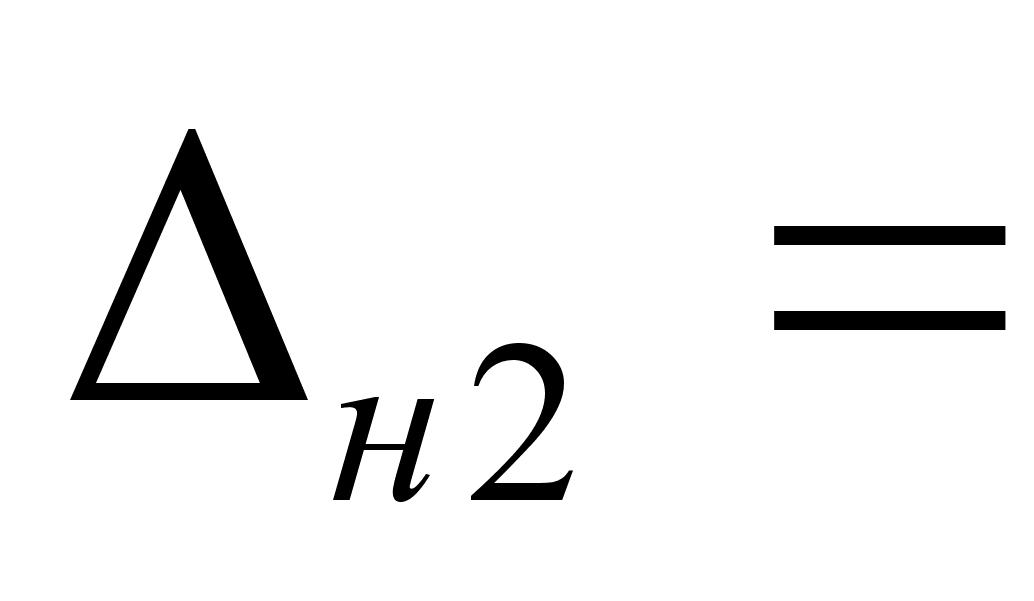 0 -
0 - -0,005 мм
-0,005 мм
 мм
мм
 0,05 -
0,05 -
 0
0
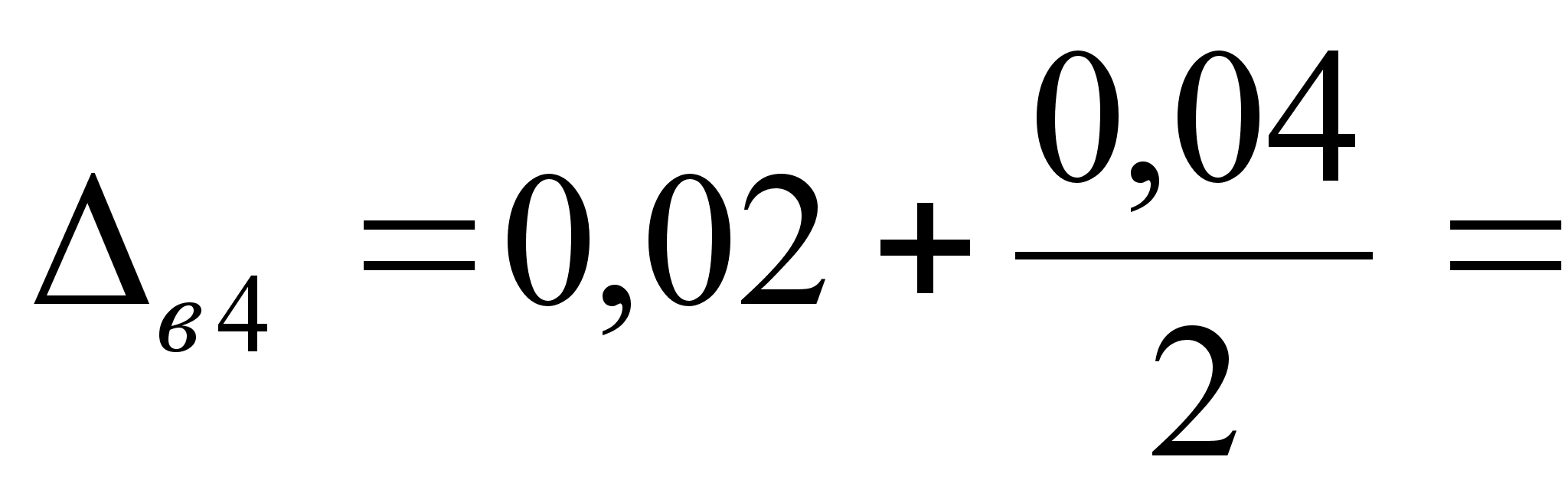 +0,04 мм
+0,04 мм
 0
0
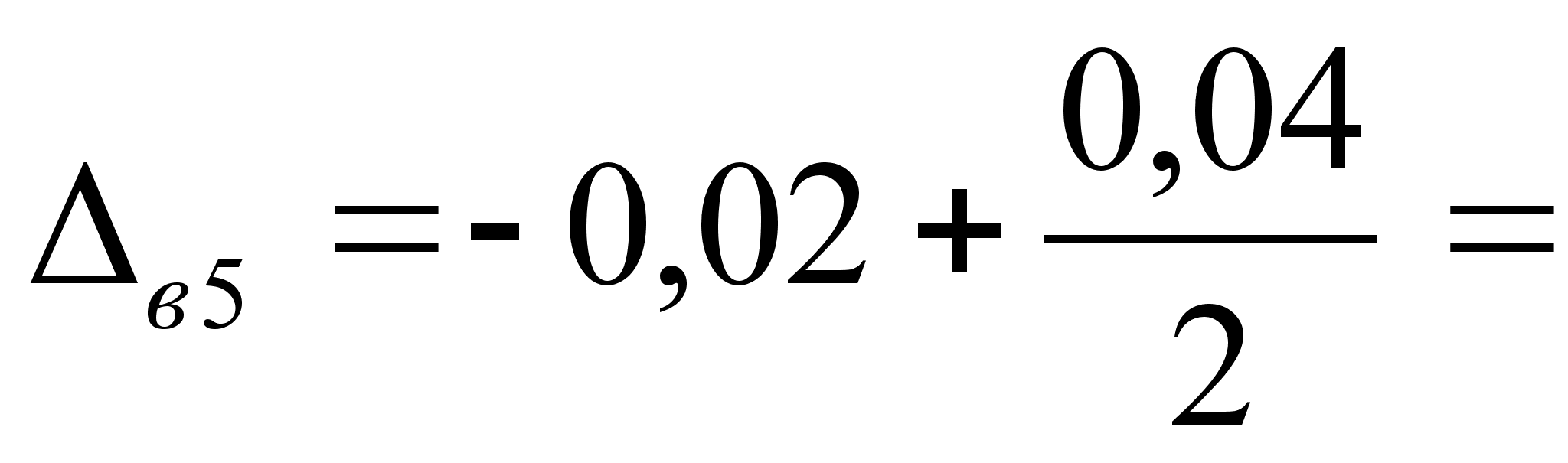 0
0
 -0,04 мм
-0,04 мм
Ответ
|
 Метод размер,
мм
Метод размер,
мм
|
Максимума-минимума |
Теоретико-вероятностный |
|
А1
|
160
+0,01
|
160
+0,02
|
|
А2
|
28
+0,01
|
28
0,005
|
|
А3
|
100
+0,05
|
100
+0,1
|
|
А4
|
125
–0,025
|
125+0,04
|
|
А5
|
135
–0,025
|
135-0,04
|
Список
использованной
литературы
ГОСТ
16320-80 «Цепи размерные.
Методы расчета
плоских
цепей.»
ГОСТ
6636-69 «Номинальные
линейные размеры»
Якушев
А.И., Воронцов
Л.Н., Федотов
Н.М. «Взаимозаменяемость,
стандартизация
и технические
измерения»
Москва «Машиностроение»
1987 г.
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ
ИНСТИТУТ
ЭЛЕКТРОНИКИ
И МАТЕМАТИКИ
( ТЕХНИЧЕСКИЙ
ИНСТИТУТ )
КУРСОВАЯ
РАБОТА
НА ТЕМУ:
РАСЧЁТ
РАЗМЕРНЫХ ЦЕПЕЙ
( СТАНДАРТИЗАЦИЯ
)
ВАРИАНТ
№ 8
Студент:
Меньшов
А.В.
Группа: И-42
Преподаватель:
Гусакова
Л. В.
Москва,
1998 год.
|