И.П.Иванов
Теоретическая физика, несмотря на многочисленные успехи, до сих пор сталкивается с задачами, которые она должна, но пока не может решить. Многие из таких задач возникают при попытке объяснить макроскопические свойства тел, исходя из их микроскопического строения. В этой заметке рассказывается о том, как выглядят исследования в этой области на примере, казалось бы, безобидной задачи о теплопроводности одномерной цепочки атомов.
Теоретическая физика и проблема микроскопического описания тел
Теоретическая физика интересна и сама по себе, однако, ее красота и сила проявляются в самой полной форме тогда, когда с ее помощью удается описать какое-либо наблюдаемое явления, какой-то кусочек нашего мира. Когда вместо эмпирических полуописательных формул, то работающих, то не работающих в той или другой области параметров, вдруг возникает единое простое уравнение, которое охватывает сразу все случаи. Когда вдруг приходит понимание, что какое-то непонятное ранее явление вовсе не "лишнее", а с необходимостью следует из общих свойств нашего мира. Когда из нескольких утверждений теоретическая физика форсированно выводит все наблюдаемые явления.
Хорошо бы, если бы так было всегда. Но, к сожалению, до сих пор есть много неуклюжих моментов, когда теоретическая физика, стартуя с простых и общих правил, запутывается в дебрях математики и не может "пробиться" к какому-то реально наблюдаемому явлению. В результате ученые временно вынуждены описывать такое явление с помощью мнемонических правил и приближенных формул. Оно может уже даже применяться в науке и в промышленности, но когда теоретик снова возвращается к этому эффекту, внутри него возникает грызущее чувство: приручить-то приручили, а понять толком не можем. Что-то ускользает.
Такие проблемы часто возникают при попытке описать макроскопические тела с микроскопической точки зрения. С одной стороны, мы знаем, что все состоит из атомов и молекул, которые взаимодействуют друг с другом по вполне понятым законам. С другой стороны, с макроскопической точки зрения, мы видим вокруг себя бесконечное разнообразие веществ и материалов с самыми необычными свойствами. Поэтому возникает серьезная задача для теоретической физики - связать эти две картины, вывести макроскопические свойства вещества (например, плотность, теплоемкость, температура плавления и кипения, вязкость, поверхностное натяжение, теплопроводность и многие другие), исходя из его микроскопического строения. То есть, выяснить, как же это так происходит, что движение отдельных атомов, в конце концов, образует некое сплошное вещество с присущими только ему свойствами.
Частично теоретическая физика эту задачу решила. Самый простой пример: свойства разреженных газов. Исходя из очень простой, но достаточно правдоподобной модели (газ - это молекулы, хаотично летающие по сосуду и сталкивающиеся со стенками), теорфизика смогла объяснить, что такое давление газа и чему оно равно. Другими словами, если раньше уравнение состояния газа PV = nRT являлось чисто экспериментальным фактом, то теперь оно было выведено из такой микроскопической картины.
Однако ситуация не столь безоблачна, когда речь о конденсированном состоянии вещества: то есть, о жидкостях и твердых телах. Конденсированное состояние представляет для теории гораздо большую проблему, нежели разреженные газы. Ведь в газах столкновения молекул достаточно редки, так что ими можно или пренебречь совсем, или учесть с хорошей точностью в приближении парных, тройных и т.д. столкновений. В жидкости или в твердом теле все совсем не так. Там каждая молекула постоянно взаимодействует сразу с несколькими соседями, и поэтому поатомное описание такого процесса невозможно.
Здесь приходится прибегать к хитростям: строить точно решаемые модели либо пытаться провести численный анализ. Иногда это работает, иногда нет. Судя по количеству публикаций в этой области, можно с полным на то основанием сказать, что это - один из передних фронтов современной теоретической физики.
Теплопроводность одномерной цепочки: постановка проблемы
Одна из нерешенных проблем в этом направлении - вывести теплопроводность кристаллической решетки хотя бы в одномерном случае, то есть показать, как именно одномерная цепочка атомов проводит "тепло". Казалось бы, что в этом трудного! Рассматриваем одномерную цепочку атомов, связанных некими силами, пишем определенный вид межатомного взаимодействия, и запускаем модель на численный счет. Это, в самом деле, сделать несложно, но вот только результаты получаются крайне неудовлетворительные.
Что значит "неудовлетворительные"? Взгляните на Рис.1, где показан стационарный профиль температуры внутри какого-нибудь макроскопического тела. Если с одной стороны тела поддерживается высокая температура, а с другой - низкая, то в теле возникает поток тепла, который и приводит к возникновению показанного профиля температур. Это и есть явление теплопроводности. Интересно выяснить, будет ли такая же картина получаться и в результате численного моделирования нашей одномерной цепочки.
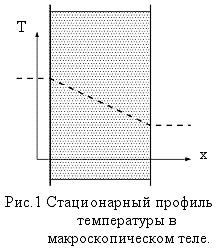
Оказывается - ничего похожего. На Рис.2 показано, как меняется профиль локальной температуры цепочки в зависимости от количества атомов в ней. Мы видим, что чем больше частиц в цепочке, тем меньше походит результат моделирования на реальное физическое явление. Другими словами, попытка описать на уровне атомов такое простое явление как теплопроводность кристалла не увенчалась успехом: с увеличением числа частиц теплопроводность кристалла стремится к бесконечности.
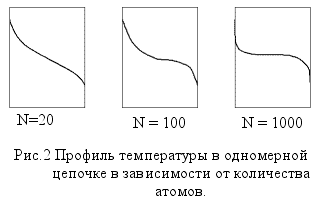
Ситуация, конечно же, тревожная. Ведь мы же понимаем, что кристаллические твердые тела имеют решетку, мы понимаем, какие силы действуют между атомами этой решетки. Так почему же не удается описать такое казалось бы понятное явление?!
Проблема эта стоит перед теоретиками достаточно давно, и долгое время все попытки придумать хотя бы одну модель, которая демонстрировала бы конечный, не зависящий от количества частиц коэффициент теплопроводности, заканчивались крахом. Зато появлялись результаты, которые еще более усугубляли проблему: например, строгое доказательство того, что в так называемых интегрируемых моделях теплопроводность обязана быть бесконечной [1]. Но ведь весь мир вокруг нас демонстрирует совершенно противоположный эффект! Так где же тут подвох? Неужели наши представления о микроскопической структуре твердых тел неверны? Или может быть, мы выбираем не те модели для межатомного взаимодействия? А может быть есть какие-то глубокие проблемы внутри статистической физики или в квантовой теории атомов и молекул?
Правильный путь, возможно, найден
Эти вопросы мучили теоретиков несколько десятилетий. И лишь в последнее время усилиями нескольких исследовательских групп начало приходить понимание (точнее, пока что только подозрение на понимание), что главную роль в этом явлении должен играть детерминированный хаос (хаотическое поведение системы под действием вовсе не хаотического воздействия). Именно он, по-видимому, ответствен за возникновение разнообразных необратимых явлений в системах, микроскопическая эволюция которых обратима во времени.
Как же хаотичность в одномерном кристалле может помочь нашей проблеме? В работе [2] предлагается следующее описание эффекта. В строго периодической цепочке возникают коллективные колебания, фононы, которые распространяются вдоль цепочки без затухания, без какого-либо "трения". Эти фононы, двигаясь от одного края цепочки к другому, и переносят тепло. В реальности же фононы, возникающие в кристаллических телах, рассеиваются, гасятся на случайных неоднородностях, на случайных возмущениях решетки. В результате механизм переноса тепла в реальных телах - не фононный, а диффузионный, то есть "от частицы к частице".
Вполне естественно желание проверить, будет ли такой механизм "гашения" фононов работать и в нашей модели. Итак, вводим в модель какую-либо хаотичность, какой-нибудь беспорядок. Например, в работе [2] массы частиц в цепочке были не одинаковы, а случайно менялись в некоторых определенных пределах от одной частицы к другой. При всей искусственности такого предположения, это все-таки некий способ ввести в модель хаотичность. Для сил межатомного взаимодействия выбиралось несколько различных моделей.
Результаты моделирования поведения такой цепочки выглядят обнадеживающими. Ученым удалось найти несколько моделей, в которых профиль температуры стремился к прямой (Рис.1) при увеличении числа частиц. Однако было обнаружено, что это происходит вовсе не для всех типов межатомных потенциалов. В частности, крайне важной оказалась ангармоничность потенциала (т.е. потенциал должен был иметь вид не U = k(x1 - x2)2/2, а, например, U = k(x1 -x2)2/2 + b(x1-x2)4/4): ангармоническая добавка обеспечивала неинтегрируемость модели.
Авторы работы пришли к выводу, что существуют, по крайней мере, два необходимых условия для возникновения нормальной теплопроводности: неинтегрируемость системы и присутствие детерминированного хаоса. Однако авторы признают, что, несмотря на некоторые успехи, полного понимания в этой области до сих пор нет.
Список литературы
[1] Z.Rieder et al, J. Math. Phys. 8 (1967) 1073.
[2] B.Hu, B.Li and H.Zhao, Phys.Rev.Lett. 86 (2001) 63; Phys.Rev.E 61 (2000) 3828.
|